双参数问题的处理

张立建

(江苏省建湖高级中学，224700)

双参数问题的处理

张立建

(江苏省建湖高级中学，224700)

双参数问题是近几年高考的热点问题之一,这类问题背景多样,联系到的知识面非常广,对学生的要求高,着重考察学生的知识迁移、联想构造、综合分析解决问题的能力．本文浅谈双参数问题的处理方法．

一、主元变更

一般地,若问题中有两个参数,我们把已知范围的参数作为主元(自变量),要求的参数作为参数,求其范围．

例1(2015年江苏高考题) 已知函数

f(x)=x3+ax2+b(a,b∈R).

(1)试讨论f(x)的单调性；

分析本题第(2)问中将b=c-a代入即可消掉参数b．故实质是两个参数a,c的问题．学生根据函数f(x)有三个不同的零点,易得参数a满足的条件,是学生熟悉的问题．但随着参数c的引入,在处理c和条件a的联系时,学生思维定势,大多认为a为参数,不能转变为a为自变量,思维受阻,摸不着头脑．其实,因为a的范围已知,故选定a作主元,c作参数,即可突破难点,则问题转化为函数的最值问题,也是学生熟悉的题型,不难求解.

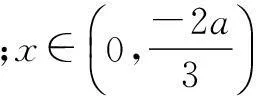
评注此题若分解为两个独立的题目,一是已知函数的零点个数求参数范围,二是已知含参数的不等式恒成立,求参数的取值范围我们的学生做起来可能游刃有余.但两个问题整合在一起,在衔接处的处理,等价转化,思维的转变上,往往就做得不好，这说明学生的学习往往有“形”无“实”，平时过于重视题型、解题方法,在能力的培养上没有达到相应的高度.

二、整体换元

例2已知函数f(x)=lnx,函数y=f(x)的图象上任意不同的两点A(x1,y1),B(x2,y2),线段AB的中点为C(x0,y0),记直线AB的斜率为k,试证明:k>f′(x0)．

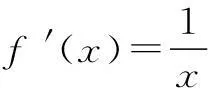
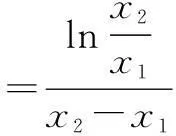
设x2>x1.要证k>f′(x0),只要证

又因为x2>x1,所以只要证

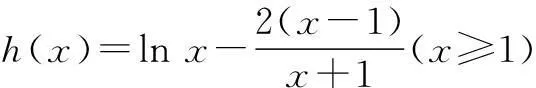
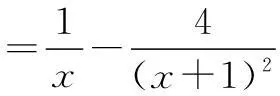
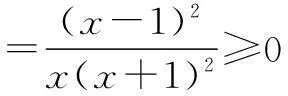
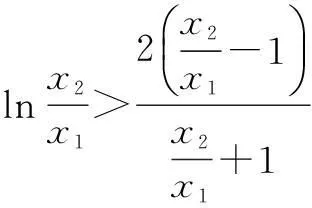
三、消元

例3已知函数f(x)=ex-1+x-2,g(x)=x2-ax-a+3,若存在实数x1,x2使得f(x1)=g(x2)=0,且|x1-x2|≤1,求实数a的取值范围．

分析难点在于条件f(x1)=g(x2)=0只能说明x1,x2分别是函数f(x)、g(x)的零点,且x1,x2没有联系,无从下手．注意观察到函数f(x)的解析式已知,可以求出x1的值,这是解题的题眼．因此问题转化为函数g(x)在约束条件|x1-x2|≤1下有零点的问题．

评注此题的关键是:两个参数x1,x2互不相干,且已知一个参数,实质为含一个参数求范围的问题．

四、选元

例4(同例2)

证明不妨设x1>x2.

要证明k>f′(x0),即证明

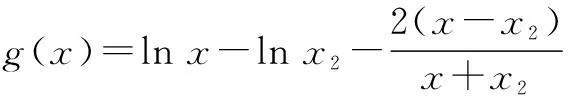
其中x>x2>0,则

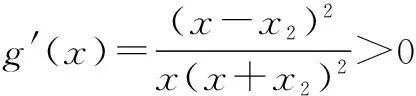
例5已知函数f(x)=xlnx,当a>0,b>0时,求证:f(a)+f(b)≥f(a+b)-(a+b)ln 2．

分析本题有两个参数a,b,三个结构a,b,a+b,故消元变成只含有两个结构,再将一个视为主元,一个看作参数求解．

证明即证f(a)+f(a+b-a)≥f(a+b)-(a+b)ln 2.令a+b=k,k>0,则转化为证明f(a)+f(k-a)≥f(k)-kln 2．

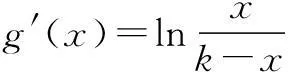
五、函数与方程思想

分析根据题意可以得到关于两个参数a,b的方程组,解方程组解出参数的值．

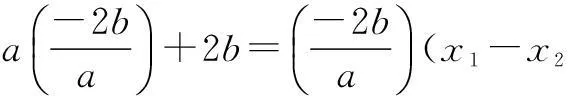
解得a=2．

评注此题难点在两个方程的求解．