解析几何定点问题探究
2016-07-07江中伟
江中伟
(广东省大埔县虎山中学,514299)
○学习指导○
解析几何定点问题探究
江中伟
(广东省大埔县虎山中学,514299)
近几年高考中常常出现有关解析几何的定点问题. 解决这些问题的思维障碍在于:一是定点究竟在哪里;二是面对字母运算不得要领,难以找到合理的突破口而陷入繁杂的运算. 本文试图通过近几年的高考(或模拟)试题的分析,对定点问题的常见类型和对应的解题方法做逐一的介绍;通过这些方法的介绍,使得学生在运算能力,简化运算的策略等方面有所提高.
一、直线恒过定点问题

(1)求椭圆C的标准方程;
(2)若直线l:y=kx+m与椭圆C相交于A、B两点(A、B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点A2,求证:直线l过定点,并求出该定点的坐标.


(2)设A(x1,y1)、B(x2,y2),将y=kx+m代入椭圆方程,得
(4k2+3)x2+8kmx+4m2-12=0.
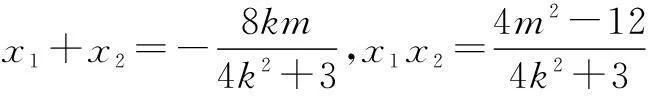
y1=kx1+m,y2=kx2+m.
∵以AB为直径的圆过椭圆右顶点A2(2,0),

∴(x1-2,y1)·(x2-2,y2)
=(x1-2) (x2-2)+y1y2
=(x1-2) (x2-2)
+(kx1+m) (kx2+m)
=(k2+1)x1x2+(km-2) (x1+x2)
+m2+4

整理得 7m2+16km+4k2=0,

当m=-2k时,直线l为y=k(x-2),恒过定点A2(2,0),不合题意舍去;

评注解决动直线恒过定点问题的一般思路是设出直线y=kx+m(k存在的情况);然后利用条件建立k与m的关系借助于点斜式方程确定定点坐标.
例2(2013年陕西高考题)已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(1) 求动圆圆心的轨迹C的方程;
(2) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q, 若x轴是∠PBQ的角平分线, 证明直线l过定点.
解(1)y2=8x.(过程略)
(2) 设直线l的方程为y=kx+b,与y2=8x联立可得k2x2-(8-2kb)x+b2=0(其中Δ>0).设P(x1,kx1+b),Q(x2,kx2+b),若x轴是∠PBQ的平分线,则

即k=-b.
故直线l的方程为y=k(x-1),直线过定点(1,0).
二.动圆恒过定点问题

(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q. 试探究: 在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

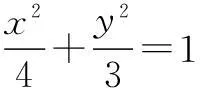
4k2-m2+3=0,
(*)
由x=4与y=kx+m,得
xQ=4,yQ=4k+m.
假设平面内存在定点M满足条件,由图形对称性知,点M必在x轴上.


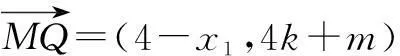


故存在定点M(1,0),使得以PQ为直径的圆恒过点M.
实际上,本题也可以先用特殊情况探路得出以PQ为直径的圆过点M(1,0),再证明一般情况下也成立(同理有些直线恒过定点问题也可以用此法). 又如:
(1)求椭圆C1的方程;
(2)证明:无论点T运动到何处,圆C3恒经过椭圆C1上一定点.

(2)设点T的坐标为(x0,y0),圆C3的半径为r.
∵点T是抛物线C2上的动点,

∵圆C3与y轴交于M,N两点,且|MN|=4,


∴圆C3的方程为

(*)
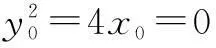
此时圆C3的方程为
x2+y2=4.
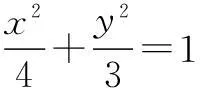
分别把点(2,0)和(-2,0)代入方程(*)检验,可知点(2,0)恒符合方程(*),点(-2,0)不恒符合方程(*).
因此无论点T运动到何处,圆C3恒经过椭圆C1上的定点(2,0).
评注本题的求解充分运用了特殊到一般的数学思想,其优越性体现在定点的确定指明了探究的方向,从而将动态探索的问题转化为定点证明(检验)的问题,大大降低了问题的难度.
