高一数学测试
2016-07-07
○课外测试○
高一数学测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.2sin15°cos15°=______.
2.若x是1和5的等差中项,则x=______.
3.等比数列{an}中a5=1,a8=8,则公比q=______.
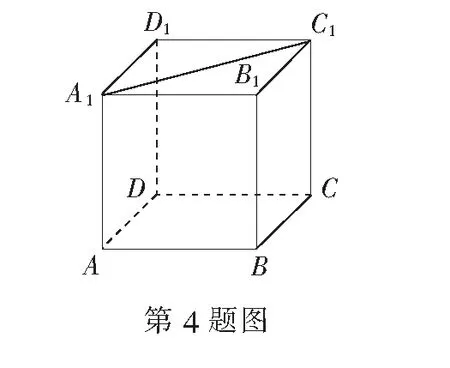
4.如图,正方体ABCD-A1B1C1D1中,异面直线A1C1与BC所成角的大小为______.
5.已知Sn是等比数列{an}的前n项和,若a1=1,公比q=2,Sn=511,则n=______.
6.已知正项等比数列{an}的前n项和为Sn,S3=3,S9=21,则S6=______.
8.一个蜂巢里有1只蜜蜂,第1天,它飞出去找回3个伙伴;第2天,4只蜜蜂飞出去,各自找回了3个伙伴.如果该过程继续下去,第n天(n∈N*) 所有的蜜蜂都归巢后,蜂巢中蜜蜂的只数为______.
10.已知数列{an}中,a1=1,an+1=an+2n+1(n∈N*),则数列{an}的通项公式an=______.
11.已知等差数列{an}中,a1>0,公差d<0,Sn是其前n项和,S3=S19,使得Sn取最大值时,n的值为______.
12.已知数列{an}的通项公式是an=-n2+12n-32,其前n项和是Sn,则对任意的n>m(其中m,n∈N*),Sn-Sm的最大值是______.
二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分14分)∆ABC中,A,B,C所对的边分别是a,b,c,且2bcosB=acosC+ccosA.
(1)求B的大小;
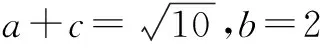
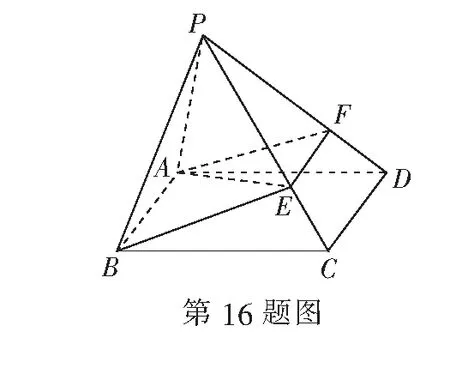
16.(本小题满分14分)如图,四棱锥P-ABCD中,ABCD是平行四边形.
(1)求证:AB∥平面PCD;
(2)E是线段PC上一点,且PE=2EC,设平面ABE与直线PD的交点为F,求PF∶FD的值.
17.(本小题满分15分)已知等差数列{an}的公差d≠0,a2,a4,a8依次成等比数列,a6=24,数列{an}的前n项和为Sn.
(1)求an,Sn;
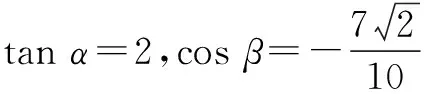
(1)求cos 2α的值;
(2)求2α-β的值.

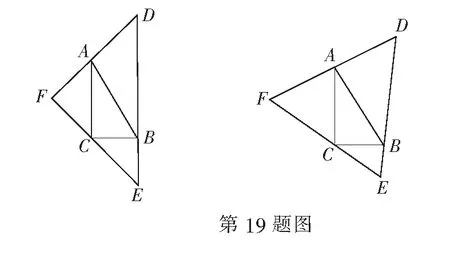
方案1:扩大为一个等腰直角三角形DEF,其中斜边DE过点B,且与AC平行,DF过点A,EF过点C;
方案2:扩大为一个等边三角形DEF,其中DE过点B,DF过点A,EF过点C.
(1)求方案1中∆DEF面积S1的值;
(2)在方案2中,设∠DBA=θ,用θ表示∆DEF的边长f(θ),并求出∆DEF面积S2的最大值.
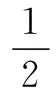
(1)当m=12时,求a2 016的值;
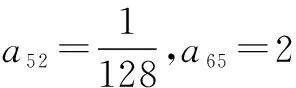
(3)是否存在m,使S128m+3≥2 016成立,若存在,求出m的值;若不存在,请说明理由.
参考答案
一、填空题
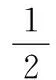
5. 9;6.9;7.两解;8.4n;
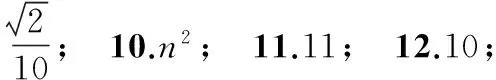
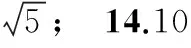
二、解答题
15.(1)∵2bcosB=acosC+ccosA,
∴2sinBcosB=sinAcosC+sinCcosA,
∴2sinBcosB=sin(A+C)
=sin(π-B)=sinB.
∵B∈(0,π),∴sinB>0,
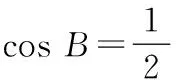
(2)∵b2=a2+c2-2accosB,
∴a2+c2-ac=4.
①
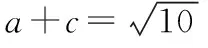
∴(a+c)2=a2+c2+2ac=10.
②
由①②,得ac=2.
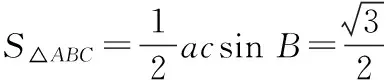
16.(1)∵ABCD是平行四边形,
∴AB∥CD,
又∵AB⊄平面PCD,CD⊂平面PCD,
∴AB∥平面PCD.
(2)∵平面ABE与直线PD的交点为F,
∴EF⊂平面ABE.
∵AB∥平面PCD,
平面ABE∩平面PCD=EF,
∴AB∥EF. ∵AB∥CD,
∴EF∥CD,∴PF∶FD=PE∶EC=2.
17.(1)∵a2,a4,a8依次成等比数列,
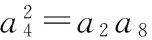
即(a1+3d)2=(a1+d)(a1+7d),
整理,得a1d=d2.
∵d≠0,∴a1=d.
又∵a6=a1+5d=24,
∴a1=d=4,
∴an=4n,Sn=2n2+2n.
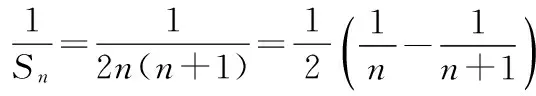
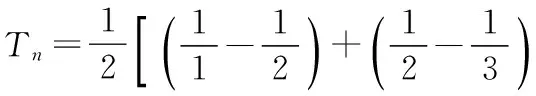
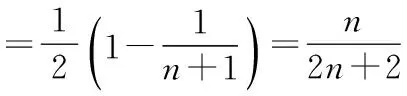
18.(1)解法1因为tanα=2,所以
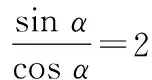
又sin2α+cos2α=1,
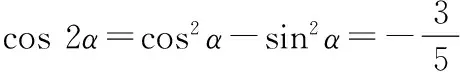
解法2cos 2α=cos2α-sin2α
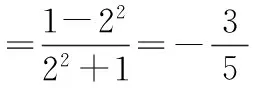
(2)解法1因为α∈(0,π),且tanα=2,
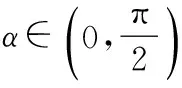
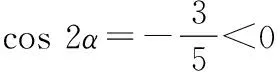
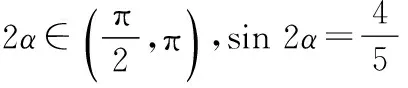
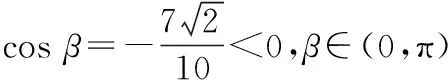
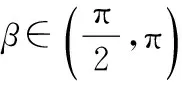
所以sin(2α-β)=sin 2αcosβ-cos 2αsinβ

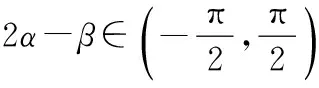
解法2因为α∈(0,π),且tanα=2,
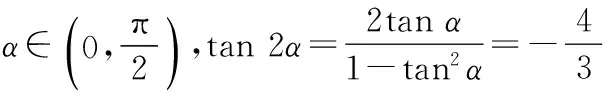
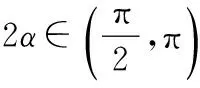
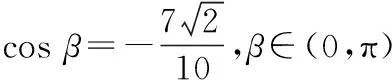


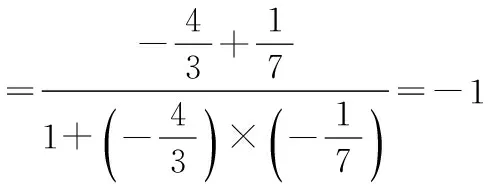
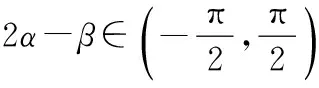
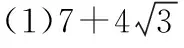
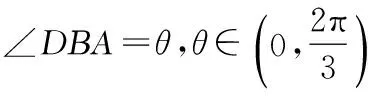


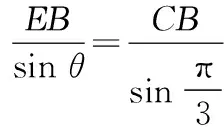
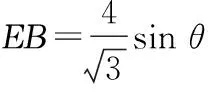
则等边三角形的边长
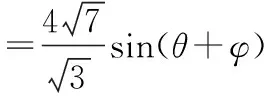
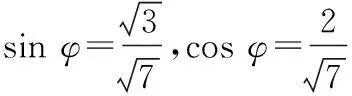
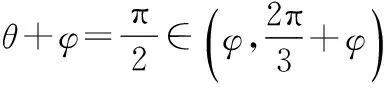
20.(1)an+24=an,所以a2 016=a24,
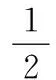
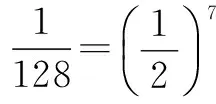

2km+m+7=(2k+1)m+7=52,
即(2k+1)m=45,
其中m≥7,m∈N,k∈N.
当k=0时,m=45,成立;
当k=1时,m=15,成立;
当k=2时,m=9成立;
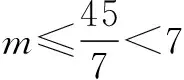
所以m可取9,15,45.
同理由a65=2,m可取30,15,10,6.
综上得m=15.
(3)S128m+3=64S2m+a1+a2+a3
≥2 016,
由于m是整数,左边最大值是30,不等式不可能成立,所以不存在这样的m.
