由一道联考题看极坐标的应用

高丰平

(湖北省孝昌县第二高级中学，432900)

由一道联考题看极坐标的应用

高丰平

(湖北省孝昌县第二高级中学，432900)

本文先给出2016年3月湖北省七市(州)高三联合考试理科第20题：

题目已知圆心为H的圆x2+y2+2x-15=0和定点A(1,0),B是圆上任意一点,线段AB的中垂线l和直线BH相交于点M,当点B在圆上运动时,点M的轨迹记为曲线C.

(1)求C的方程;

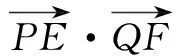
解法1(直角坐标法)

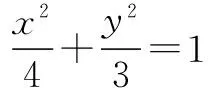
(2)由直线EF与直线PQ垂直,可得

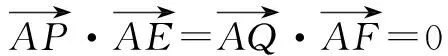
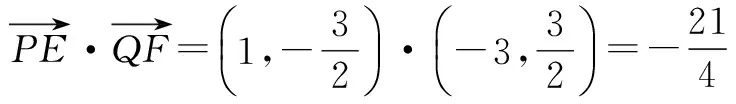
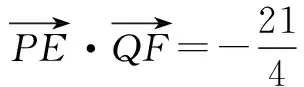
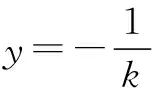
(3+4k2)x2-8k2x+4k2-12=0,

=(1+k2)[xP·xQ-(xP+xQ)+1]

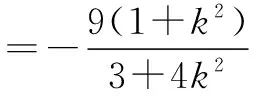
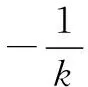
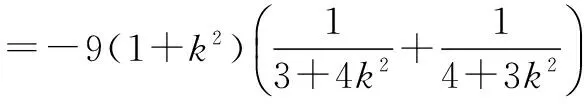
令1+k2=t,则t>1,上式成为

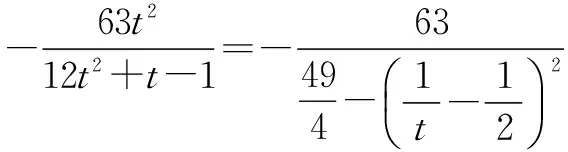
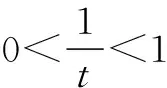
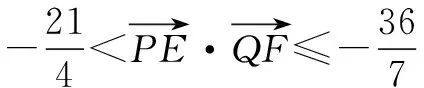
解法2(1)同上.

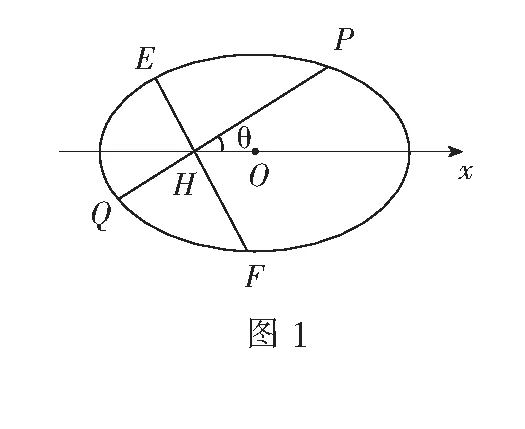
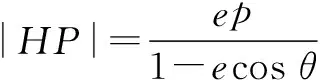
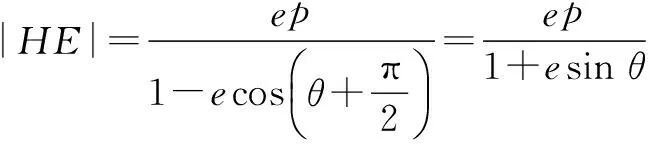
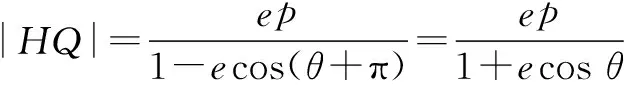
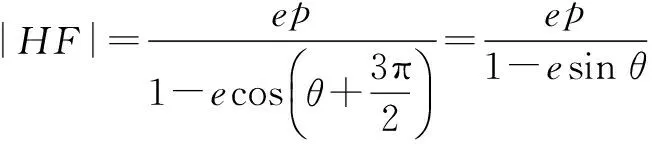
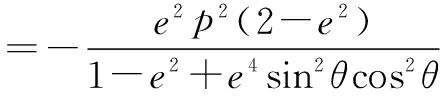
评注比较可见，相对于解法1,用极坐标有更少的代数运算,讨论也更加简单,其可操作性也更强.下面再举两例.

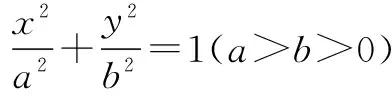
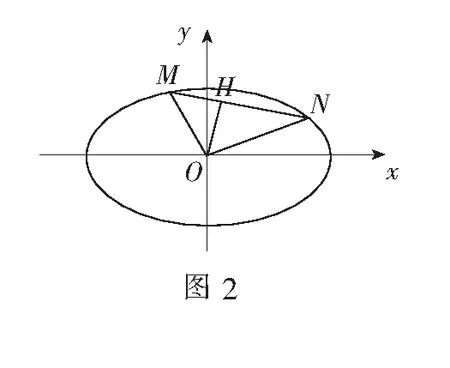
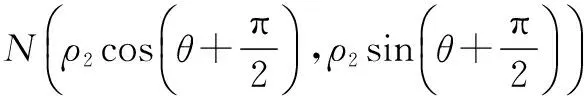
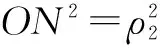
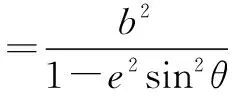
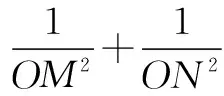
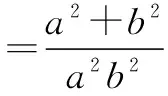
过点O作OH⊥MN,H为垂足,在直角三角形MON中,根据勾股定理，有

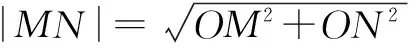
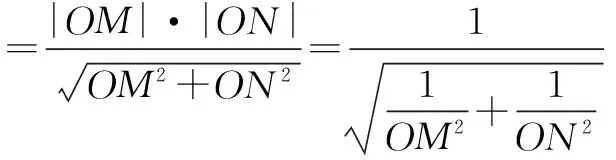
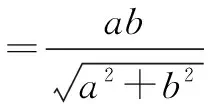
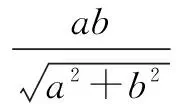
评注本例没有用圆锥曲线的极坐标方程,但极坐标与参数方程的应用结合在一起，体现了极坐标在解题过程中的灵活性.

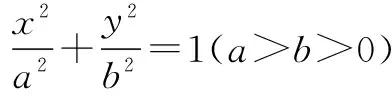
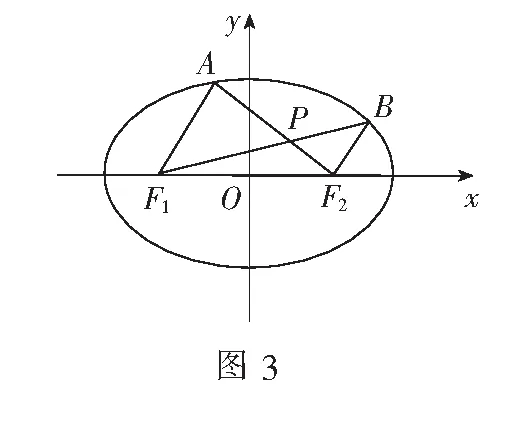
(1)求椭圆的方程;

(2)设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.

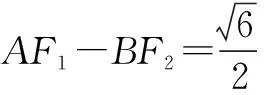
(ii)求证:PF1+PF2是定值.

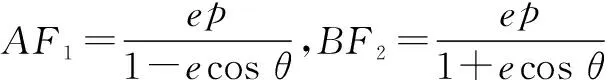
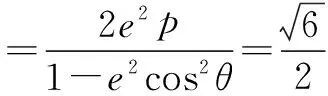
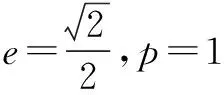
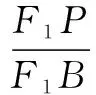
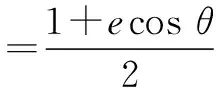
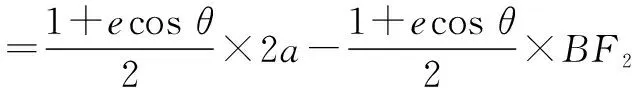
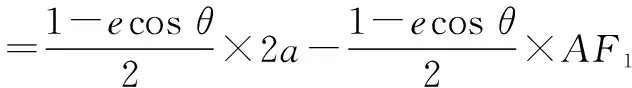
所以PF1+PF2=2a-ep

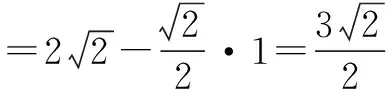
综上可见，正确地使用极坐标,可以避免复杂的计算,避免复杂的分类讨论.在处理焦点弦的问题中,应用极坐标,会使这方面的问题变得简单,也能够提高解题的能力,通过类似的总结和探究,同学们学习圆锥曲线的兴趣必将大大增加.