基于PSO-LSSVM的网络流量预测

刘春茂，郝倩，张云岗



基于PSO-LSSVM的网络流量预测

刘春茂，郝倩，张云岗

摘 要：流量预测是计算机网络管理的一项关键技术，以提高网络流量预测的准确性为目标，本文提出一种粒子群优化算法和最小二乘支持向量机的网络流量预测模型。首先对网络流量历史数据进行混沌分析，重构网络流量样本集，然后采用粒子群算法优化最小二乘支持向量机对网络流量数据进行建模，最后采用仿真模拟实验对网络流量的预测结果分析。实验结果表明，其模型可以描述网络流量的变化趋势，获得高精度的网络流量预测结果，提供了一种新网络流量预测工具。

关键词：网络流量预测；最小二乘支持向量机；粒子群优化算法；核函数参数选择

0 引言

近年来，随着上网用户的不断增加，Internet的规模急剧增加，网络数据以及种类如图像、视频等越来越多，网络拥塞越来越严重，从而增加了网络管理难度［1］。网络流量预测可以了解将要发生的网络行为，预测结果有助于管理人员分析网络安全状况，并提出相应的管理和防范措施。因此，网络流量的建模与预测具有重要的意义［2］。

近些年来，人们对网络流量预测问题重视程度越来越高，许多学者和专家花了大量的时间和心血进行网络流量的建模与预测研究，取得一系列的研究成果［3，4］。传统网络流量预测模型为线性建模方法，如自回归（AR）模型，差分自回归滑动平均（ARIMA）模型以及多元线性回归模型，它们根据网络流量历史数据之间的变化关系，分析网络流量的变化特点以及将来的变化态势，对于小规模网络，它们的建模效率高、预测精度高［5-7］。网络流量受到外界因素影响越来越多，传统模型虽然简单、易实现，但不能准确反映复杂多变的网络流量变化特性［8］。为此，一些学者提出了一些非线性网络流量建模方法，如神经网络、支持向量机等，它们具有非线性和自适应建模能力，能够拟合网络流量的变化特点，预测精度得到了提高［9-11］。在网络流量实际建模与预测过程中，神经网络是一种基于“大数定理”的建模方法，对网络流量的历史样本数据要求大，因此，对于小规模的历史样本数据，神经网络的预测结果不稳定，许多样本点出现过拟合缺陷［12］。对于小样本数据，支持向量机的预测准确高，但对于大规模的网络流量数据，支持向量机的训练时间长，建模效率低，不符合网络流量管理中的实时性建模与预测要求［12］。最小二乘支持向量机（LSSVM）是一种专门解决支持向量机建模效率低、神经网络过拟合缺陷的机器学习算法，更加符合网络流量的非线性建模要求。参数好坏直接反映了LSSVM的网络流量预测准确性，当前有交叉验证算法、遗传算法确定LSSVM参数，但它们自身存在着一些不足，如遗传算法的交叉概率、变异概率没有理论指导，全凭经验确定，网络流量预测性能有待进一步改善［13］。

为了提高网络流量预测的准确性，提出一种粒子群优化算法和最小二乘支持向量机的网络流量预测模型，该模型对网络流量历史数据进行混沌处理，然后最小二乘支持向量机进行建模，并采用粒子群算法优化其参数，最后仿真模拟实验结果表明，本文模型可以描述网络流量的变化趋势，获得高精度的网络流量预测结果。

1 相关理论1.1 最小二乘支持向量机

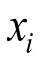
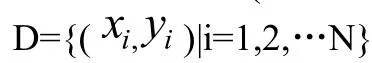
LSSVM回归为公式（1）：

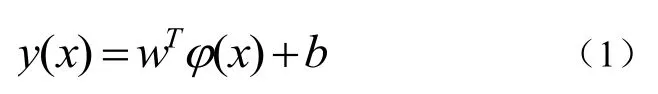
LSSVM训练过程可以看作如下优化问题如公式（2）：

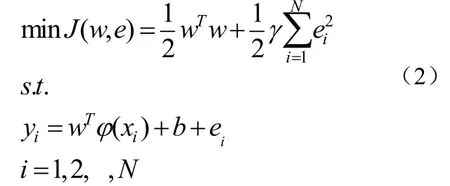
公式（2）中，γ为可调整正则化参数。

为了简化运算，提高效率，引入Lagrange函数把式（2）变成为公式（3）：

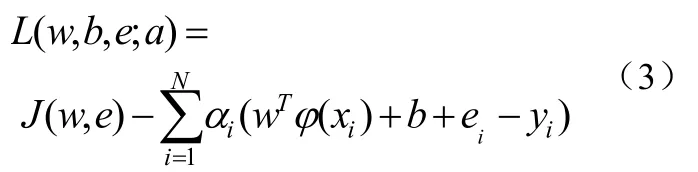
式中，

为Lagrange乘子。

对L对求偏导为，消除变量w和：

和b的解，

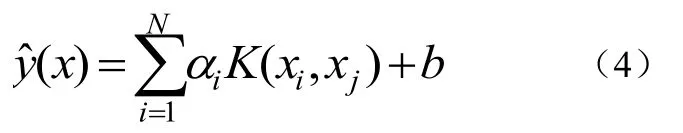
其定义如公式（5）：：

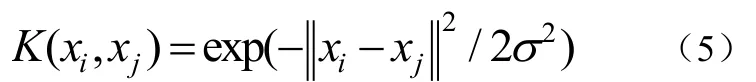
1.2 粒子群优化算法

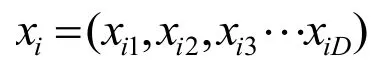
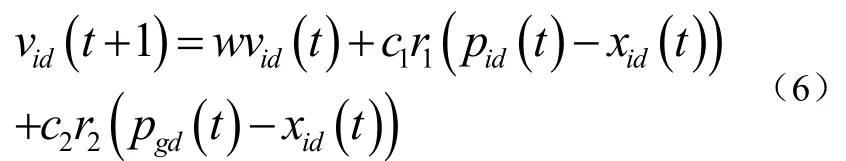
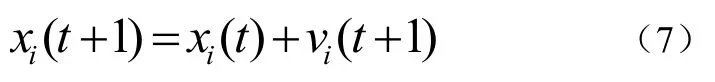
2 PSO-LSSVM的网络流量预测模型

2.1 LSSVM参数寻优的数学模型

参数γ和σ直接决定了LSSVM的网络流量拟合效果，γ值越大，网络流量的拟合精度就越高，而网络流量预测结果的泛化能力就差，而σ值越小，网络流量会出现欠学习缺陷，计算复杂度大，运行效率低。同时σ值越大，网络流量的拟合和预测误差均大，预测精度比较低，为了解决该难题，本文提出采用粒子群优化算法选择LSSVM的参数，将LSSVM的参数（γ，σ）看作是一个组合优化问题，那么（γ，σ）的数学模型为公式（8）：

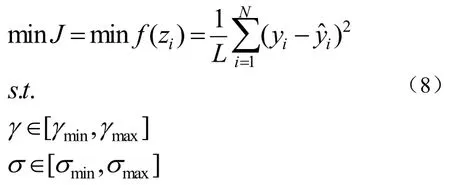
2.2 具体设计

2.21 粒子编码机制

由于PSO算法与LSSVM参数（γ，σ）之间建立联系才能进行寻优求解操作，本文采用实数编编码方式将（γ，σ）组成一个粒子，具体如图1所示：

图1 粒子的编码机制

2.22 个体适应度函数

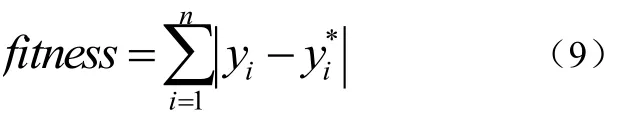
PSO-LSSVM的工作步骤

（1）对网络流量历史样本进行混沌处理，确定其嵌入维和延迟时间，得到一个有规律的网络流量数据序列。

（2）确定LSSVM参数（γ、σ）的范围，并初始化PSO算法的参数，如最大迭代次数等。

（3）随机产生初始的粒子群，每一个粒子包括（γ，σ）两部分，并且设置初始迭代次数t=0。

（4）对于网络流量训练样本，每一组参数作为LSSVM学习参数，通过10折交叉验证法计算每一个粒子的适应度值。

（5）根据适应度值确定每一个粒子的当前优位置pbest和粒子群的当前最优位置gbest。

（6）根据公式（6）和公式（7）更新粒子的速度和位置，产生新的粒子群。

（7）近代次数自加，即有t=t+1。

（8）判断PSO算法的终止条件，如何满足就根据粒子群的最优位置gbest得到最优的（γ、σ）值，不然转步骤（4）继续寻优。

（9）根据最优的（γ、σ）值和网络流量训练样本，建立基于PSO-LSSVM的网络流量预测模型。

综合上述可知，基于PSO-LSSVM的网络流量建模与预测流程如图2所示：

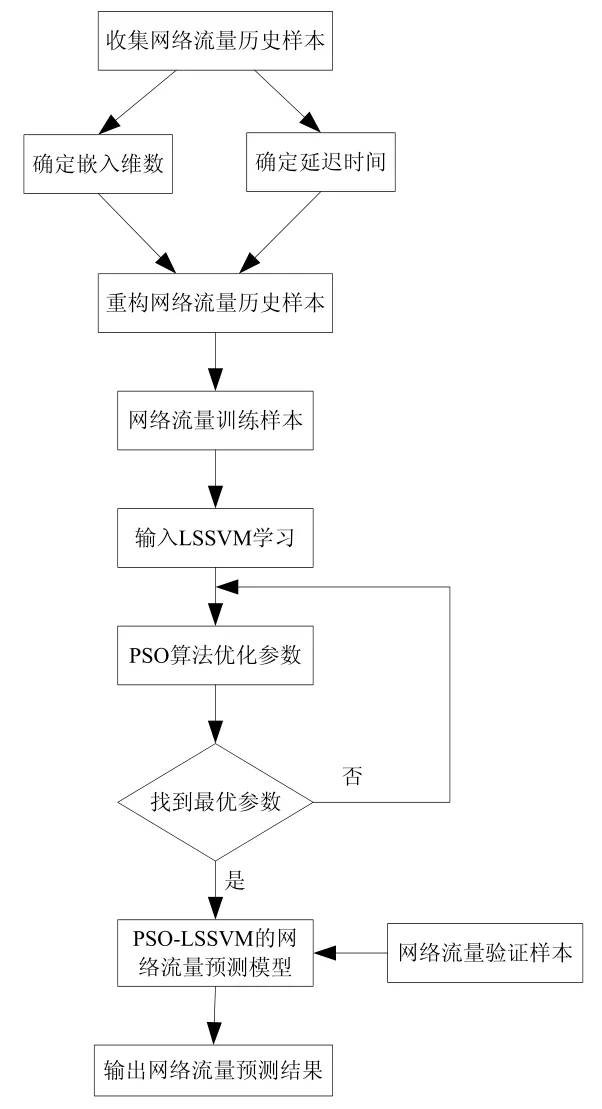
图2 PSO-LSSVM的工作流程

3 PSO-LSSVM的网络流量预测实例

3.1 源数据

为了分析PSO-LSSVM的网络流量预测性能，选择http://news.ntu.edu.tw/stat/的2014年5月1日到2014年5月16日每小时的流量作为实验对象，共得到30个流量数据，选择最后100个数据测试对PSO-LSVM的泛化性能，具体如图3所示：

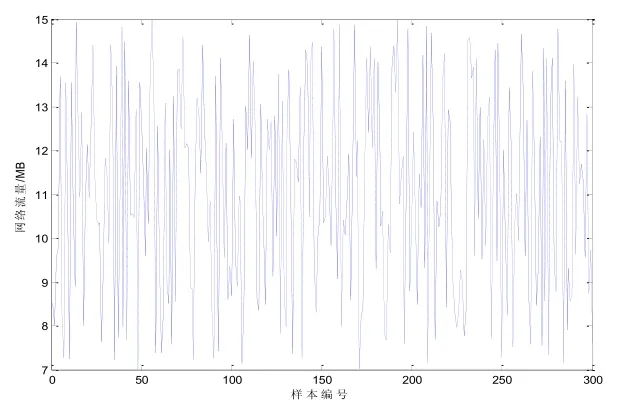
图3 实验流量

对比模型

选择时间序列模型（ARIMA）、BP神经网络（BPNN）和遗传算法优化最小二乘支持向量机（GA-LSSVM）进行对比实验，采用2种评价标准评价模型的性能，它们分别为：预测准确率（Accuracy）和均方根误差（RMSE），具体定义如公式（10）、公式（11）：

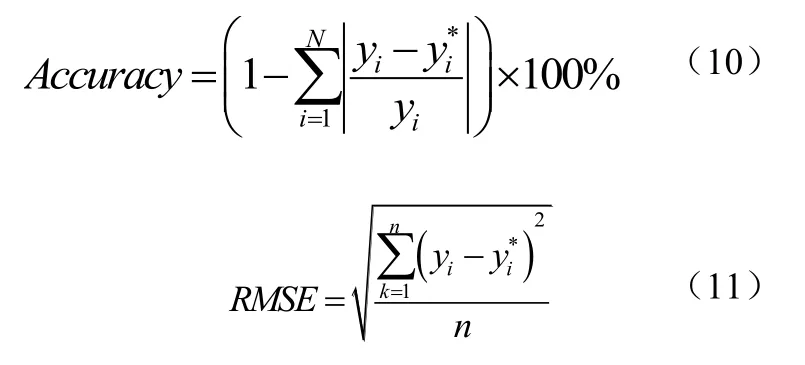
样本集的建立

网络流量受到上网人行为、网络价格等因素影响，因此其不仅具有一定的变化规律，同时具体一定的混沌性，为此，需要对图3的网络流量进行混沌处理，找到延迟时间（τ）和嵌入维数（m）从而准确描述网络流量的变化特点，分别采用自相关法和假近邻法确定τ和m，结果如图4所示：

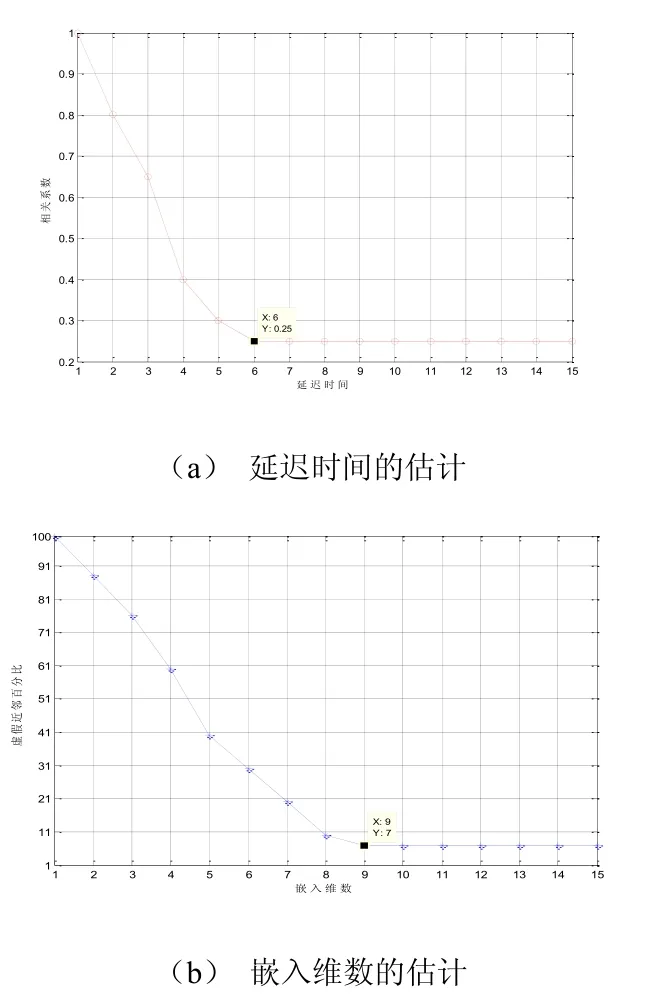
图4 样本集的建立

当τ=6时，网络流量之间的相关性变小，这样可以认为此时τ=6最合理；当m=9时，样本点的假近邻数不再发生变化，趋于稳定，这样可以认为此时m=9最合理，根据τ=6，m=9对网络流量数据进行处理，建立PSO-LSSVM的样本集。

预测结果与分析

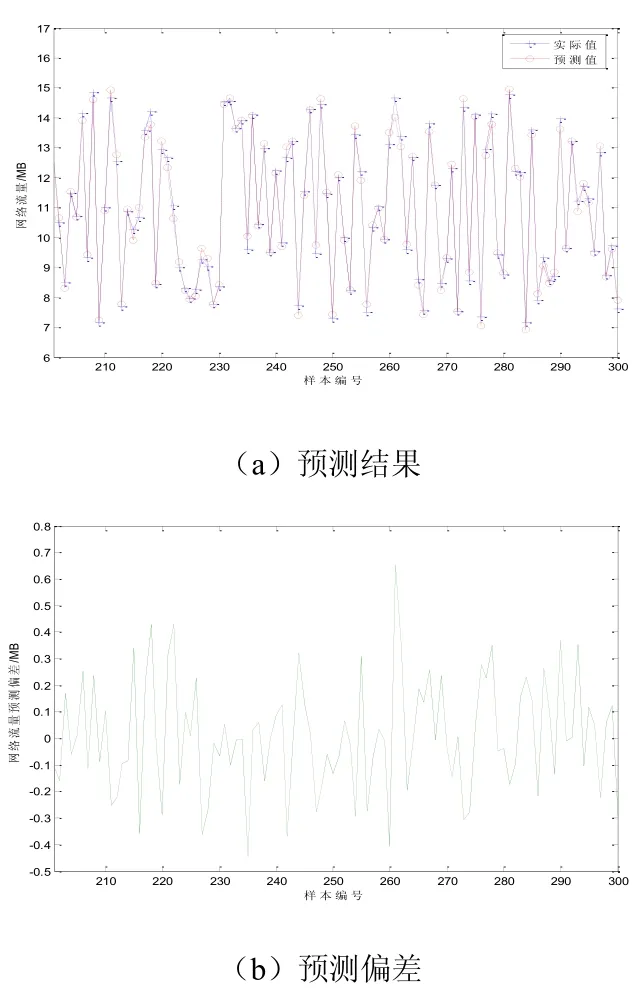
图5 PSO-LSSVM的预测结果

采用LSSVM对前200个网络流量数据进行学习，并采用PSO算法对LSSVM的参数（γ，σ）进行估计，最终选择γ=10.755，σ=0.158作为LSSVM的网络流量建模最优参数，从而网络流量的预测模型，测试样本的预测结果如图5所示：在图5（a）中，PSO-LSSVM可以很好描述该种网络流量数据的变化特点，预测值与实际值拟合精度相当的高，这说明PSO-LSSVM可以从网络流量的历史数据中找到网络流量将来的变化趋势，网络流量预测结果的泛化能力好。从图5（b）可发现，PSO-LSSVM的预测值与实际网络流量值的偏差小，而且整个网络流量偏差波动控制在一定的范围内，PSO-LSSVM可以准确刻画了网络流量的非线性、周期性变化特点，是一种精度高、泛化能力强的网络流量预测模型。对PSO-LSSVM与当前网络流量流行预测模型的性能进行对比分析，统计它们的预测结果的Accuracy和RMSE，具体如表1所示：

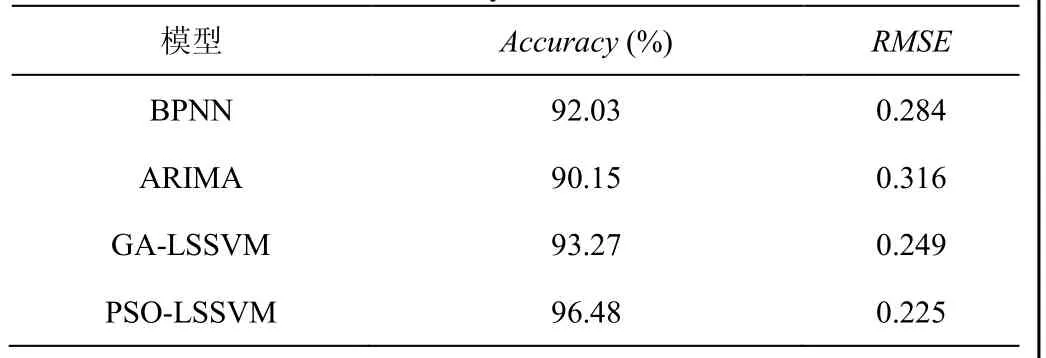
表1 Accuracy和RMSE对比

对表1中各模型的Accuracy和RMSE进行对比，我们可以发现，对于两种评价指标，PSO-LSSVM均优于所有当前网络流量预测模型，如：BP神经网络，对比实验结果表明，PSO-LSSVM可以获得比PSO-LSSVM更理想的网络流量预测结果。

4 总结

针对当前LSSVM核函数以及参数选择问题，为了提高网络流量预测精度，本文提出一种PSO-LSSVM的网络流量建模方法，并通过仿真实验对其性能进行测试，可以得到如下结论：

（1）网络流量受到许多外界影响因素的作用，具有复杂的非线性和时变性，采用嵌入维和延迟时间对网络流量历史样本进行重构，能够得到一个有规模的网络流量数据样本，有助于后续的网络流量建模。

（2）核函数以及参数不同，得到的LSSVM的预测性能不同，针对具体网络流量数据，通过PSO算法的寻优能力在所有LSSVM参数寻找最合理的参数，减少网络流量训练过程中的支持机量少，网络流量的预测精度和建模效率均得到了不同程度的改善，而且优于当前的流行网络流量预测模型。

网络流量预测的准确性不仅与LSSVM参数相关，实际与网络流量训练样本长度密切相关，如何选择最合理的网络流量训练样本，以进一步提高网络流量预测精度，这是我们下一步将要进行的研究。

参考文献

［1］ 党小超，阎林. 基于多元线性自回归模型的流量预测［J］.计算机工程， 2012，38（1）:84-89

［2］ 邹柏贤，刘强. 基于ARMA模型的网络流量预测［J］. 计算机研究与发展， 2002， 39（12）: 1645-1652

［3］ 段智彬，孙恩昌，张延华，董燕. 基于ARMA模型的网络流量预测［J］. 中国电子科学研究院学报， 2009，4（4）:325 -356.

［4］ 张冉，赵成龙.ARIMA模型在网络流量预测中的应用研究［J］. 计算机仿真， 2011， 28（1）: 171-174

［5］ 胡玉清，谭献海，宋正阳.基于FARIMA的网络建模与性能分析［J］. 计算机工程与设计， 2008， 29（18）: 4666-4714

［6］ Clegg R G. A Practical Guide to Measuring the Hurst Parameter ［J］. International Journal of Simulation: Systems，Science & Technology， 2006， 7（2）:3-4

［7］ 马华林，李翠凤，张立燕. 基于灰色模型和自适应过滤的网络流量预测［J］. 计算机工程， 2009，35（1）:130-152

［8］ 洪飞，吴志美. 基于小波的多尺度网络流量预测模型［J］.计算机学报，2006，29（1）:166-171

［9］ 刘杰，黄亚楼. 基于BP神经网络的非线性网络流量预测［J］. 计算机应用，2007，27（7）:1770-1772

［10］ 王俊松，高志伟.基于RBF神经网络的网络流量建模与预测［J］. 计算机工程与应用， 2008， 44（13）:7-11

［11］ 曹建华，刘渊，戴悦. 一种基于灰色神经网络的网强流量预测模型［J］. 计算机工程与应用， 2008，44（5）:155-157.

［12］ 王治. 基于混沌粒子群优化SVR的网络流量预测［J］.计算机仿真， 2011， 28（5）: 151-154.

［13］ 周辉仁， 仁仙玲. 最小二乘向量机的参数优选方法及应用［J］. 系统工程学报， 2009， 24（2）: 248-252.

Network Traffic Forecast Based on PSO-LSSVM

Liu Chunmao， Hao qian， Zhang Yungang
（Henan Polytechnic Institute， Nanyang 473000， China）

Abstract:Network traffic forecasting is a key technology in computer network management. In order to improve the accuracy of network traffic forecasting， a network traffic forecasting model based on particle swarm optimization algorithm and least square support vector machine is proposed in this paper. Firstly， it analyzes the historical data of network traffic by chaotic theory， and reconstructs the network traffic sample. And then， particle swarm optimization algorithm optimizing least square support vector machine is used to model the network traffic data. Finally， the simulation results are used to test the forecasting results of network traffic. Experimental results show that the proposed model can describe the change trend of network traffic， and obtain the high accuracy of network traffic forecasting results， which provides a new tool for network traffic modeling and forecasting.

Key words:Network Traffic Forecast； Least Squares Support Vector Machine； Particle Swarm Optimization A lgorithm； Kernel Function Parameter Selection

中图分类号：TP391

文献标志码：A

文章编号：1007-757X（2016）05-0027-04

基金项目：河南省科技攻关项目（132102210208）.

作者简介：刘春茂（1979-），男，南阳人，河南工业职业技术学院，电子信息工程系，讲师，硕士，研究方向：信息处理技术及网络管理研究，南阳，473000 郝 倩（1983-），女，南阳，河南工业职业技术学院，电子信息工程系，讲师，硕士，研究方向：计算机应用，南阳，473000张云岗（1983-），男，南阳，河南工业职业技术学院，电子信息工程系，讲师，硕士，研究方向：数据库与知识库，南阳，473000

收稿日期:（2015.10.23）