基于遗忘曲线的自适应词汇记忆模型

蔡乐，熊万强，孙晓光



基于遗忘曲线的自适应词汇记忆模型

蔡乐，熊万强，孙晓光

摘 要：进一步论述了智能词汇记忆模型选择幂函数拟合艾宾浩斯记忆曲线建立记忆的数学模型的正确性，并针对智能词汇记忆模型在自适应每个用户的记忆情况上的不足，引入含有参考模型的自适应控制系统。根据用户实际的单词测试结果和复习时刻作为反馈控制信号，再结合合理的记忆周期时间规划表来确定下一次的记忆曲线衰减系数，从而将智能词汇记忆模型改进成自适应词汇记忆模型。实验结果表明，自适应词汇记忆模型不仅对每个用户的记忆情况有良好的自适应性，还进一步减少了用户6. 23%的时间用来掌握词汇。

关键词：词汇记忆；遗忘曲线；自适应；反馈控制；艾宾浩斯

0 引言

全球化的时代已经来临，咨询传递与文化交流的需求不断提高，使得英语这门世界通用的交流语言的重要性日益突出。词汇是语言的建筑材料，它在语言的使用中起着重要的作用，词汇量直接影响着人们听、说、读、写、译等各项技能的发挥。英语词汇繁多而复杂，人们投入大量时间和精力来背单词却往往并没有达到理想的记忆效果，如何有效地记忆词汇已经成为了近年来的研究热点。

文献［1］提出了一种智能词汇记忆模型，为用户优化了单词复习计划，从而提高了记忆效率，但是在适应每个用户实际的记忆情况上仍然可以改进。本文改进了智能词汇记忆模型，做到了自适应性：采用艾宾浩斯遗忘曲线［2］刻画用户对每个单词的记忆情况，在单词记忆的临界时刻提醒并安排用户复习（测试），根据测试结果和复习时间作为反馈信号动态地调整下一次的遗忘曲线，并运用该模型对已在iOS平台研发出的“复旦智能记忆”系列App［3］作版本更新。实验结果表明，该模型具有良好的自适应性，并进一步提高了记忆效率。

1 智能词汇记忆模型

文献［1］阐述了生物记忆原理，在艾宾浩斯遗忘曲线的基础上给出了记忆的数学模型，由此建立智能记忆模型。并且在iOS平台研发出“复旦智能记忆”系列App，最后分析了实验结果。

智能词汇记忆模型存在的问题。

文献［1］没有详细比较拟合遗忘曲线的常见函数就选取幂函数建立记忆的数学模型。更重要的是，对同每个用户也只是通过测试其初次记忆精心挑选的几个单词来得到该用户的默认遗忘曲线的记忆衰减系数，此后则需要在特定时刻获取用户自我认定的记忆量，但是用户往往并不能精确地知晓自己的记忆程度（例如是80%还是90%）。因此，智能词汇记忆模型只是根据用户每次复习单词前自我认定的记忆程度来设定该单词下一次的复习时刻，没有对用户的实际记忆情况做自适应调整。

2 自适应词汇记忆模型

2.1 遗忘曲线拟合函数的选取

艾宾浩斯采用对数函数来描述遗忘曲线，给出的数学公式为［2］公式（1）：

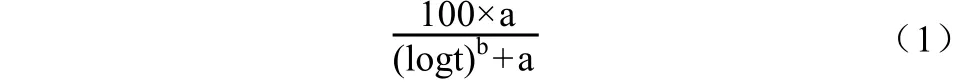
但是，艾宾浩斯在论文中没有提到采用其他函数来拟合遗忘曲线，即没有比较其他函数模型对于遗忘实验数据的拟合效果。这使得后来越来越多的心理学家对遗忘曲线的拟合提出了更多的数学模型，先后提出了100多种函数来拟合遗忘曲线，其中最有名的有对数函数、指数函数、双曲线函数、幂函数，对应的数学公式如表1所示：

表1 拟合遗忘曲线的常见函数

Chris和Robert［4］的研究指出幂函数比其他候选函数更适合用来描述艾宾浩斯遗忘曲线。因此，选用幂函数来拟合遗忘曲线，得到的数学公式为公式（2）：

其中，m为记忆保持量，无量纲；M为记忆系数常量，无量纲；Δt为时间间隔，单位min；β为记忆衰减系数，无量纲。

2.2 含有参考模型的自适应控制系统［5］

在各种形式的自适应控制系统中，含有参考模型的自适应控制系统从理论研究和实际应用上都是比较成熟的，见图1所示：

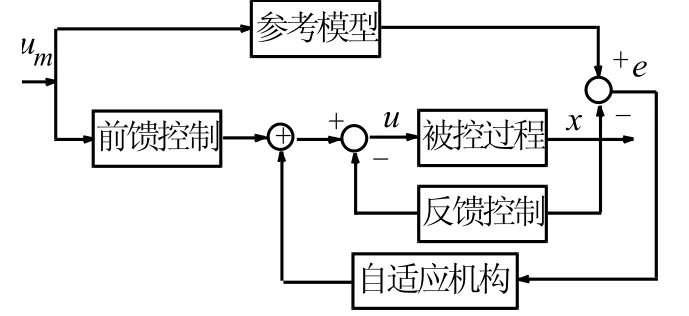
图1 含有参考模型的自适应控制系统

可以给智能词汇记忆模型引入含有参考模型的自适应控制系统：选用幂函数建立遗忘曲线的数学参考模型；用户对单词初始遗忘曲线的衰减系数作为前馈控制；用户对单词进行复习测试时，测试结果（题目做对、做错）作为反馈控制信号。随着复习次数的增加，反馈自适应系统就能够越来越准确地刻画用户对具体单词的遗忘曲线。

2.3 自适应性调整

在学习不同单词前，用户对每个单词有不同的初始认知程度（可能完全不认识，可能模棱两可，可能已经认识），因此刚学完某个单词时，用户对该单词的初始遗忘曲线的衰减系数β0不同。用户往往并不能精确地知晓自己的记忆程度，因此只能得到用户对单词的初始遗忘曲线的衰减系数β0的几个特定梯度值。

根据已经发布的“复旦智能记忆”系列单词记忆iOS App的使用数据，将用户对单词的初始认知程度分成不认识、模糊、认识3个梯度，对应的初始遗忘曲线衰减系数β0的值分别为C0=0.4307、C1=0.2038、C2=0.1056，即：不认识，β0=0.4307；模糊β0=0.2038；认识，β0=0.1056。

既然初始遗忘曲线只能得到几个特定的梯度值，那么初始遗忘曲线对用户的记忆情况只是一个近似刻画，并不准确。可以在合适的时刻对用户进行测试，根据测试结果进一步调整衰减系数β，使得遗忘曲线能更真实地反映用户的记忆情况，调整方式如图2所示：

图2 根据测试结果调整遗忘曲线

已经根据用户对单词的初始认知情况设定了衰减系数β的初始值（不认识为C0、模糊为C1、认识为C2），也就确定了初始遗忘曲线。在某个时刻t1对用户进行此单词的测试：若用户做错了测试题，则可见用户对该单词的真实记忆情况比初始曲线刻画的要差，即真实的初始遗忘曲线是一条下降更快的曲线；若用户做对了测试题，则可见用户对该单词的真实记忆情况比初始曲线刻画的要好，即真实的初始遗忘曲线是一条下降稍平缓的曲线。测试完，用户知道了正确答案，也就完成了一次复习，下一次的遗忘曲线走势与测试结果对应，做对测试题目则下一次的曲线下降更平缓，做错则下降更快。

根据测试结果的反馈，动态确定遗忘曲线的走势使其更真实地反映用户的记忆效果，能达到良好的自适应效果。至此，可以总结出完整的自适应词汇记忆模型。

2.4 自适应词汇记忆模型的定义

定义1 选用幂函数作为遗忘曲线的数学公式：m=M×Δt-β，其中m为记忆保持量，M为记忆系数常量，Δt为时间间隔，β为记忆衰减系数。

定义2 初始遗忘曲线的记忆衰减系数β0的3种梯度常量值为：C0=0.4307、C1=0.2038、C2=0.1056。在学习单词前，获取用户对该单词的初始认知程度（不认识、模糊、认识）并由此确定初始的记忆衰减系数β0：不认识，β0=C0；模糊，β0=C1；认识，β0=C2。

定义4 测试结果fd为做对、做错两种：做错，fd=0；做对，fd=1。测试结果fd将作为反馈控制信号，与当前遗忘曲线的记忆衰减系数βi共同确定下一次的遗忘曲线衰减系数βi+1，βi+1=f（βi，fd）。自适应控制函数f的选取只要合理即可，比如可以根据合理的记忆周期时间规划表［6］来构建。

遗忘是巩固记忆的基础，如果人不能忘记那些不必要的内容，那么就无法记忆那些重要的、需要识记的材料［7］。采用符合这一生物记忆特性的方法，才是最好的记忆方法，在即将遗忘的时候进行复习，效果是最好的，而且也是最省时的。而即将遗忘的一个自然界定标准就是记忆量下降了一半，这就是定义3确定记忆临界值和安排复习时间点的原则。

定义4 迭代地确定了每次复习后新的遗忘曲线记忆衰减系数，将每次复习的测试结果作为反馈信号动态地确定下一次的遗忘曲线记忆衰减系数。这样，多次复习后将会不断地自适应求精，新的遗忘曲线记忆衰减系数也就越来越真实地反映用户的记忆效果。

2.5 自适应词汇记忆模型的实现

采用自适应记忆模型编写单词记忆软件时，实现自适应记忆模型的流程图如图3所示：

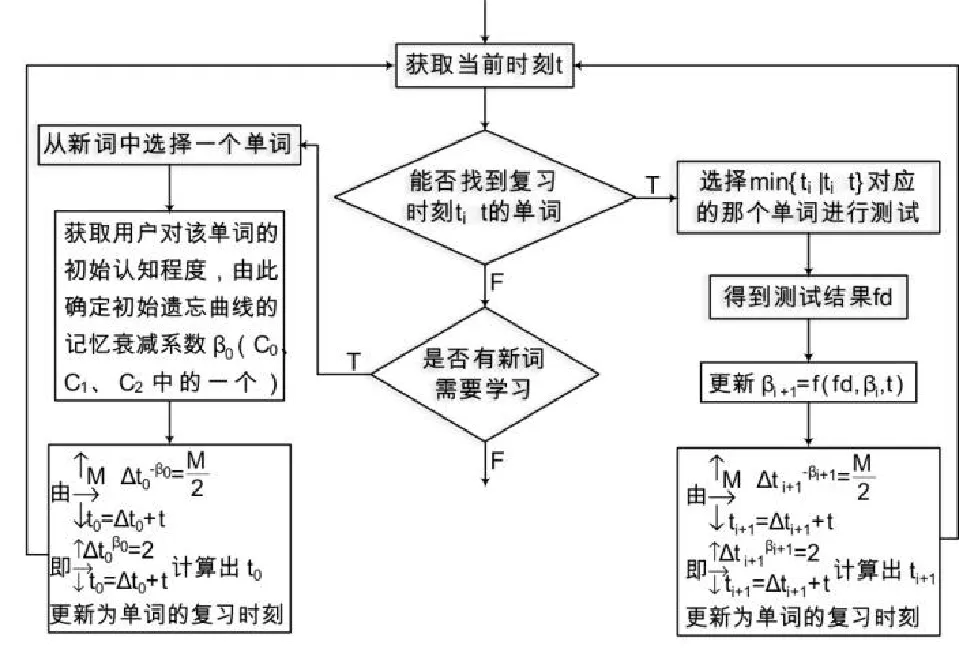
图3 实现自适应记忆模型的流程图

对比自适应词汇记忆模型的定义，可以看到自适应控制函数f比定义4多出了一个时间参数。这是因为在实际中，在t时刻可能已经有多个单词的复习时刻ti≤t，此时依据min｛ti|ti≤t｝选中一个单词安排复习，则真正的复习时刻t比理论计算得的复习时刻（为min｛ti|ti≤t｝）可能大很多，这个时候就需要引入一个时间参数来修正理论上算得的下一次的遗忘曲线记忆衰减系数βi+1：真正的复习时刻比理论计算的复习时刻大很多，那么记忆效果变差了（即衰减系数变大），因此在真正复习时刻比理论上的复习时刻大很多时，相应地再增加一个反馈控制信号——复习时刻t，将βi+1的值调大一些，自适应性效果更好。在即将遗忘的时候进行复习，效果最好，但是有多个单词超过了该复习的时刻仍然没被复习，为了让每个单词都达到最佳的复习效果，自然是从集合｛ti|ti≤t｝中从小到大依次安排每个单词的复习，这样可以让每个单词的当前遗忘程度尽量最小。因此，在多个单词需要复习时，判定规则是min｛ti|ti≤t｝。同样的道理，在有单词没复习完的情况下，优先安排旧词的复习而暂不学习新词，整体的记忆效果最佳。

选择新词学习时，可以给用户提供顺序、乱序、逆序的学习顺序选择，让用户选择适合自己记忆的位置效应［8］，帮助用户达到最好的记忆效果。在t时刻，根据用户对新词的初始记忆程度，确定首次学完新词后的初始记忆衰减系数β0后，根据定义1和定义3，用户首次复习单词的时刻t0可由下面的方程组解得公式（4）：

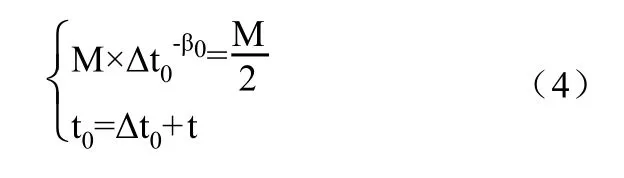
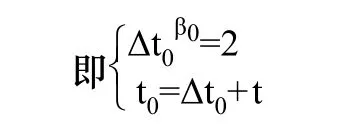
t时刻，有旧词需要复习时，它们的复习时刻的集合为｛ti|ti≤t｝，根据下式选取复习的旧词：

min｛ti|ti≤t｝

t时刻复习（即测试）完后，得到了测试结果fd，下一次的遗忘曲线衰减系数βi+1由下式计算得到：

βi+1=f（fd，βi，t）

根据定义1和定义3，下一次的复习时刻ti+1由下面的方程组解得公式（5）：

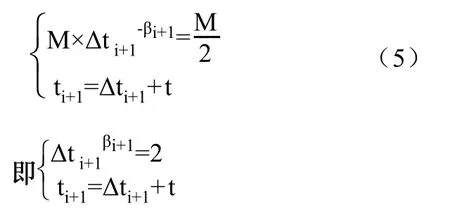
3 实验结果与分析

基于艾宾浩斯遗忘曲线的智能词汇记忆模型已经被用来研发出单词记忆软件［9］——“复旦智能记忆”系列iOSApp，进一步将智能词汇记忆模型改进后的自适应词汇记忆模型运用到该App作一个版本更新。此次实验，选取1500个托福高频词作为记忆材料的“复旦智能记忆─托福1500高频词”App［10］来收集测试数据，其用户下载量已超过700。App在每个复习时间点对单词安排了随机的干扰测试，包括选择和听写，从而测试用户的记忆情况。选择题测试为正确答案单词安排了除近义词/同义词外的3个随机干扰单词，听写题测试则是通过听单词读音来拼写单词。

软件将用户对单词的初始认知程度按认识、模糊、不认识3个梯度划分类型，分别统计这3类单词的平均记忆次数，最后将3类单词的平均记忆次数作综合平均，实验数据如表2所示：

表2 托福1500高频词平均记忆次数

采用新东方的单词记忆方法，每个单词都需要记忆9次［1］［6］。将新东方记忆、智能记忆、自适应记忆三者作对比实验，实验结果如图4和图5所示：

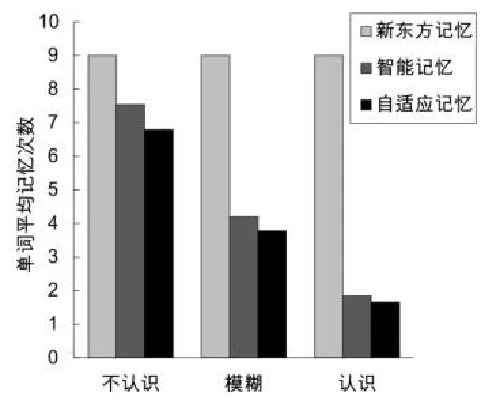
图4 各类型单词平均记忆次数对比

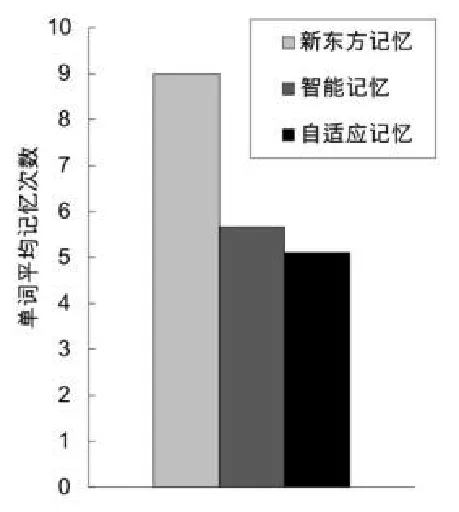
图5 所有单词平均记忆次数对比

由实验数据得出：在不影响记忆效果的同时，使用智能词汇记忆模型比新东方词汇记忆方法减少了37.04%的记忆次数，而使用自适应词汇记忆模型比新东方词汇记忆方法减少了43.27%的记忆次数。

实验结果表明，自适应词汇记忆模型比智能词汇记忆模型进一步节省了6.23%的记忆次数，不仅对每个用户的记忆情况有良好的自适应性，还进一步提高了记忆效率。

5 总结

本文进一步论述了智能词汇记忆模型选择幂函数建立记忆的数学模型的正确性，并针对智能词汇记忆模型在自适应每个用户的记忆情况上的不足，引入含有参考模型的自适应控制系统，将单词测试结果和复习时刻作为反馈控制信号，从而将智能词汇记忆模型改进成自适应词汇记忆模型。实验结果表明，自适应词汇记忆模型不仅对每个用户的记忆情况有良好的自适应性，还进一步提高了记忆效率。下一步工作将针对含有参考模型的自适应控制系统和自适应控制函数f的制定方面进行深入的研究，进一步提

升词汇记忆模型的自适应性和记忆效率。

参考文献

［1］ 熊万强，王蓓莉，孙晓光. 基于生物记忆原理的智能词汇记忆模型［J］. 计算机工程，2015，41（6）: 254-257.

［2］ Hermann Ebbinghaus. Memory: A Contribution to Experimental Psychology ［M］. New York: Columbia University， 1913: 30-89.

［3］ Xiaoguang Sun. 复旦智能记忆［CP/OL］.https://itunes. aple.com/cn/developer/xiaoguangsun/id887332701，2015-0 5-30.

［4］ Chris Donkin， Robert M. Nosofsky. A Power-Law Model of Psychological Memory Strength in Short- and Long-Term Recognition［J］. Psychological Science， 2012，23（6）: 625-634.

［5］ James Clayton Pope. Adaptive control system w ith model reference ［D］.Berkeley: Univ.of California， 1966.

［6］ 杨鹏. 17天搞定GRE单词［M］. 西安:西安交通大学出版社，2006.

［7］ Weiner B. Motivated forgetting and the study of repression［J］.Journal of personality， 1968， 36（2）:34-213

［8］ Murdock， Bennet. Serial Position Effect of Free Recall［J］. Journal of Experimental Psychology， 1962， 64（2）: 482-488.

［9］ 陈金凯，陈庆奎.基于艾宾浩斯记忆曲线的单词记忆软件设计［J］.电子技术，2013，02:1-3.

［10］ Xiaoguang Sun. 复旦智能记忆─托福1500高频词［CP/OL］.https://itunes.apple.com/cn/app/fu-dan-zhi-neng-j i-yi-tuo/id962601223， 2015-01-30/2016-02-04.6.02.26）（收稿日期:2016.02.20）

Self-adaptive Vocabulary M emory M odel Based on Forgetting Curve

Cai Le， Xiong Wanqiang， Sun Xiaoguang
（School of Computer Science， Fudan University， Shanghai 201203， China）

Abstract:This paper further discusses the correctness ofthe Intelligent Vocabulary Memory Model‘s selection power function to fit Ebbinghaus memory curve and establishmathematical model of human memory.And concerning the Intelligent Vocabulary Memory Model‘s shortcomingsin the aspect ofadaptive to each user‘s actual memory circumstance， introduced adaptive control system w ith reference model. Use the result of word test and review time as the feedback control signals according to user‘s actualmemory circumstance and combine with rational memory timeplanning table to compute the attenuation coefficient of next time‘s forgetting curve， thereby improvedthe Intelligent Vocabulary Memory Model intoSelf-adaptive Vocabulary Memory Model.The experimental results show that the Adaptive Vocabulary Memory Model not only has good adaptability for each user‘s actual memory circumstance， but also further reduce 6.23% of the time for user to memorize vocabulary.

Key words:Vocabulary Memory； Forgetting Curve； Self-adaption； Feedback Control； Ebbinghaus

中图分类号：TP311

文献标志码：A

文章编号：1007-757X（2016）05-0016-04

基金项目：上海市研究生教育创新计划项目（20130102）

作者简介：蔡 乐（1988），男，黄冈，复旦大学计算机科学技术学院，硕士研究生，研究方向：嵌入式系统及应用。上海，201203。熊万强（1989），男，内江，复旦大学计算机科学技术学院，硕士研究生，研究方向：嵌入式系统及应用。上海，201203。孙晓光（1967），男，沈阳，复旦大学计算机科学技术学院，副教授，研究方向：计算机系统结构。上海，201203。