极化码在高斯信道下的信息位选择

崔茵，倪卫明



极化码在高斯信道下的信息位选择

崔茵，倪卫明

摘 要：极化码是第一种、也是目前已知的唯一一种在任意二进制输入的对称信道下能够被证明“达到”信道容量的信道编码方法，因而受到国内外编码领域的学者的追捧。基于信道极化现象，信道可分为纯噪信道和无噪信道，如何选出无噪信道传输有用信息成为极化码编码的关键技术之一。极化码对信道类型的敏感性决定了极化码在不同的信道类型下，信息位的具体选择方式有所不同，极化码在高斯信道下的信息位选择方案将予以总结分析。

关键词：极化码；信道极化；高斯信道；信息位

0 引言

极化码自2009年被Arikan［1］提出以来，以其能被严格证明“达到”信道容量的性质，吸引了众多编码领域学者的关注。极化码利用信道极化的特性［2］，通过所谓的信道“合并”与信道“分解”，将个独立的二进制输入离散无记忆信道变为N个相互依赖的信道。这些经极化操作的信道在保持N个信道的总信道容量不变的情形下，N个相互依赖的信道的信道容量呈现出极化现象：一部分信道容量增大，一部分信道容量减小。理论证明［1］：当信道数量

时，一部分信道容量将趋于1，而其余信道的信道容量将趋于0；同时，容量趋于1的信道占总信道总数的比例为原二进制输入离散信道的信道容量这一现象被称为信道极化。然而实际中受到码长的限制，极化特性不会非常理想，但仍可利用信道极化的优良特性，选出信道容量趋于1的无噪信道传输信息，在信道容量趋于0的信道上传输固定的、接收方已知的信息。

极化码在BEC信道下的理论研究已十分成熟和完善。由于极化码对信道类型的敏感性，极化码在其他信道下的仍有很多研究要做，本文将对高斯信道的下的信息位选择做总结和分析。目前已知的将极化码应用到高斯信道下有以下3种方法：一是将高斯信道等效为等信道容量的BEC信道［3］，二是蒙特卡洛逼近方法［1］，三是高斯逼近的方法［4］。

2 信道极化

2.1 符号解释

2.2 信道合并

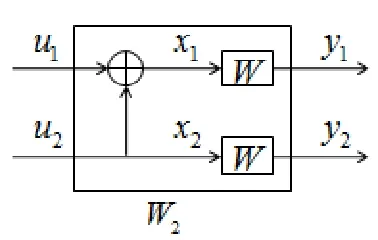
图1 合成信道?

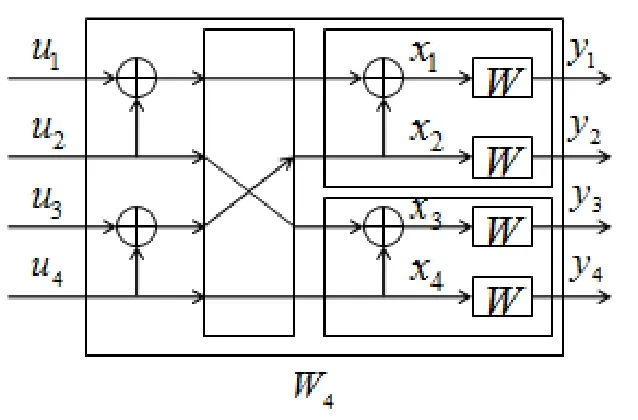
图2 合成信道W4

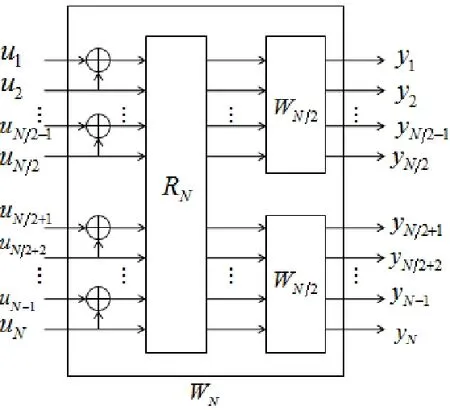
图3 合成信道WN

2.3 信道分解

通过以上分析可得，基于信道极化的这两个步骤，极化码的编码和解码过程也完成了。

3 极化码在BEC信道下的信息位选择

对于BEC信道，我们可以计算各个子信道的信道容量如公式（1）、（2）：

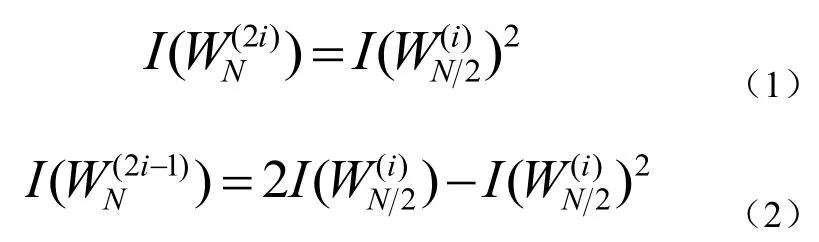
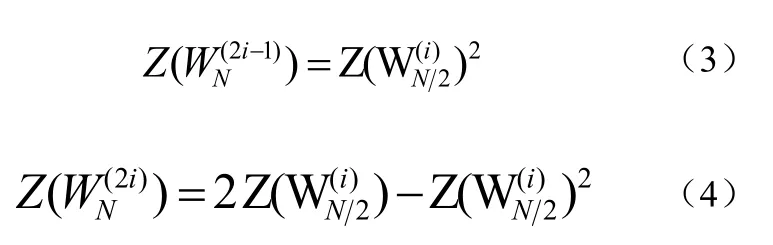
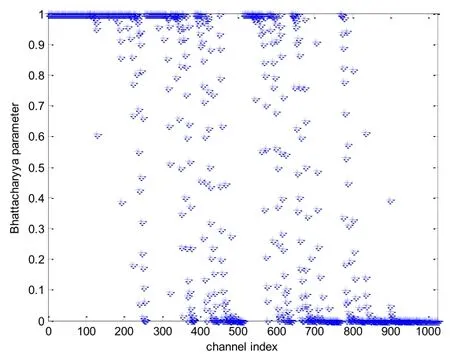
图4 BEC信道下，各个子信道的信道容量分布图

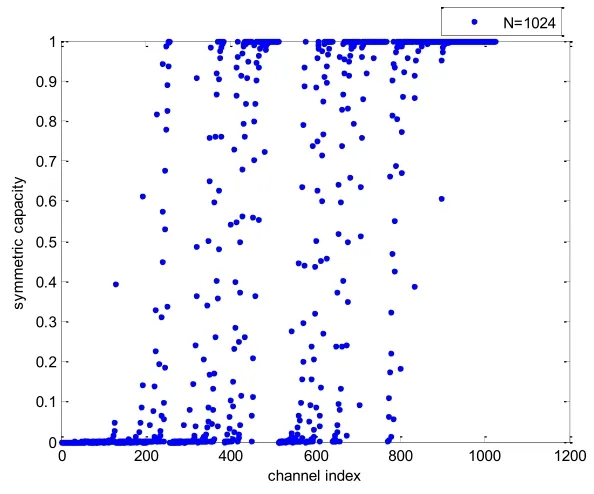
图5 BEC信道下各个自信道巴氏参数的分布图

极化码在BEC信道下的特征从以下从两个方面予以说明：

图6 码长N一定，删除概率从左至右从上到下分别为0.1，0.2，0.3，0.4，0.5，0.6时各子信道的容量分布图

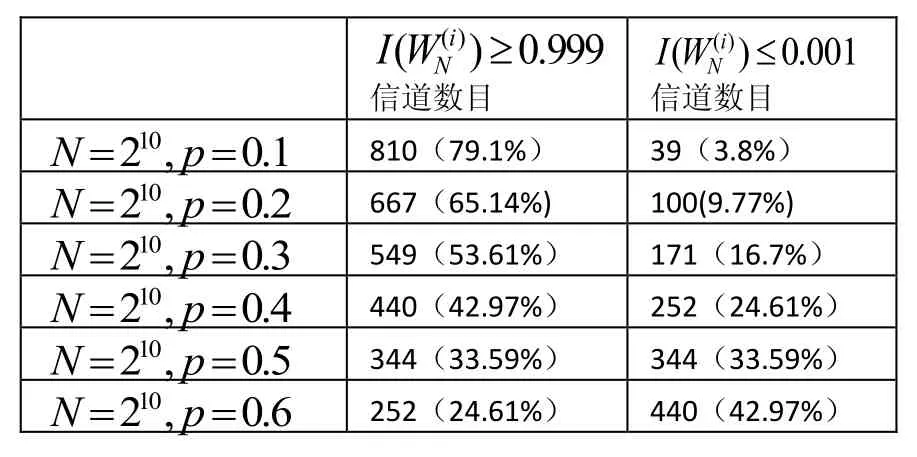
表1 码长一定，BEC信道的删除概率不定

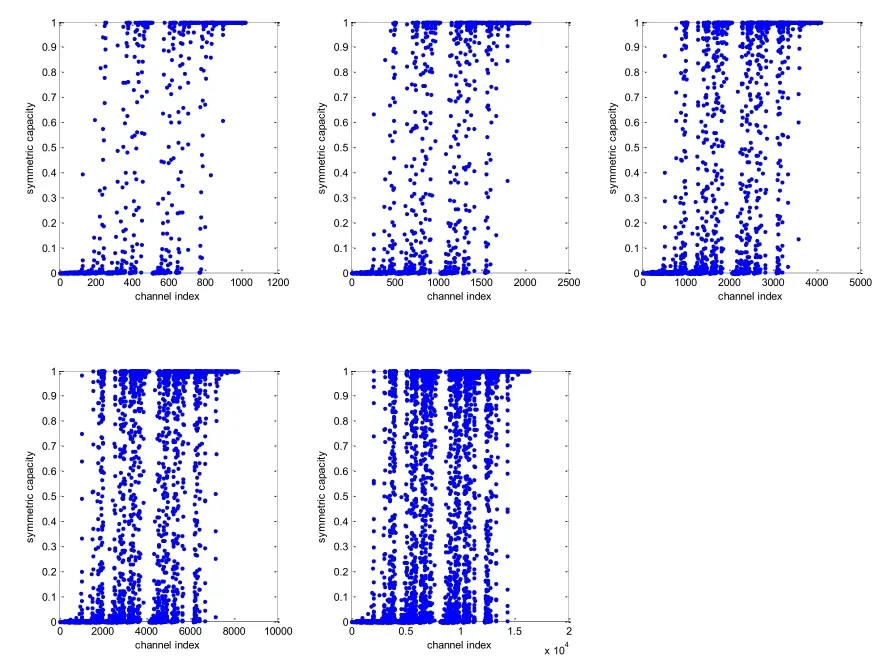
图7 删除概率一定，码长左至右从上到下分别为，，，，时各子信道的容量分布图

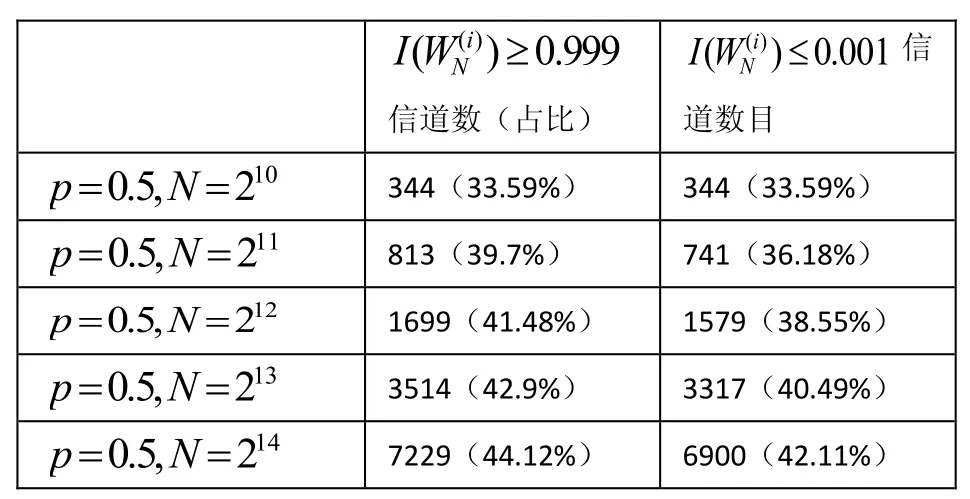
表2 码长一定，BEC信道的删除概率不定

4 极化码在AWGN信道下的信息位选择

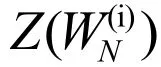
4.1 BEC等效

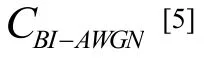
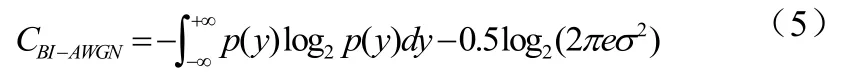
4.2 蒙特卡洛逼近

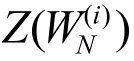
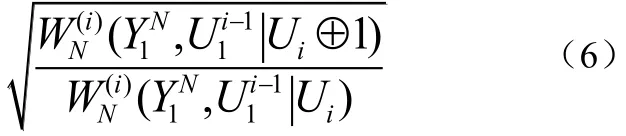
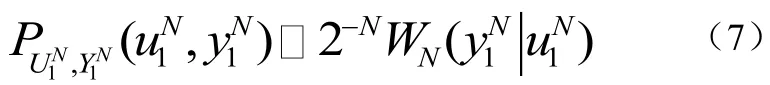
4.3 高斯逼近

在Turbo码和LDPC码中，密度进化的方法都有广泛的应用［8］［9］［10］，Tal和Vardy在对二进制输入的AWGN信道中研究Turbo码和LDPC码时，得出概率密度函数可由一簇均值为方差2倍的高斯分布来近似，将复杂的多维概率密度函数的计算简化为对一维的均值的计算，从而很大程度上简化计算量，这种对密度进化算法的简化算法称为高斯近似或者高斯逼近（GA）［6］。因此，高斯逼近算法可用于计算二进制输入AWGN信道在信道极化后信息位的选择。

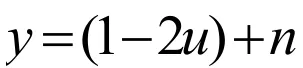
其中

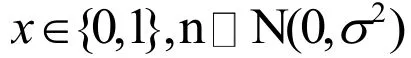
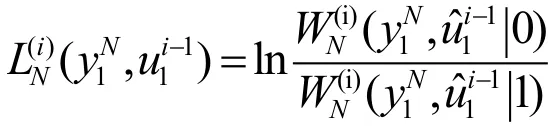
其中

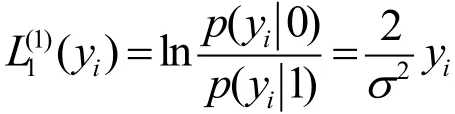
［11］如公式（8）：

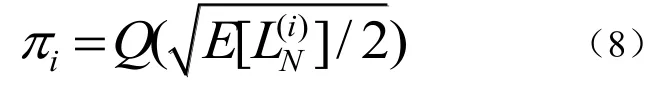
选出子信道错误概率最小的K个子信道即可完成信息位的选择。

4.3 高斯逼近

以上3种信息位的选择方法中，第二种蒙特卡洛逼近的复杂度较高，因此在信息位选择中，一般不作为常用的信息位的选择方法。在码长时，高斯白噪声的标准差，等效的BEC信道的删除概率，如图8所示：

图8 长度N=32的极化码子信道错误概率

星号表示采用BEC等效方法由公式（3）（4）得到的每个子信道的错误概率，圆圈表示采用高斯逼近方法由公式（8）得到的每个子信道的错误概率。仿真结果表示，BEC等效方法与高斯逼近方法的走势基本一致，通过高斯逼近的方法得到的子信道的错误概率较等效BEC信道方法更低。

5 总结

极化码利用信道极化的特性，将信息在可靠性高的子信道上传输，这也是极化码的关键技术之一。文中总结和分析了最常见的三种应用于高斯信道中信息位的选取方法，三种方式都是通过计算子信道的可靠性参数来选择传输信息位的子信道，同时通过对高斯信道子信道信息位选择的分析也更好的了解到极化码是一种对信道十分敏感的信道编码方法。今后的研究中，例如瑞利信道，如何去选择最可靠的K个传输信息的子信道也是非常重要的研究方向。

参考文献

［1］ Arikan .E， ―Channel polarization: a method for con

structing capacity-achieving codes for symmetric bina-ry-input memoryless channels，”［J］ IEEE Trans. Inf. Theory， July 2009，vol. 55， no. 7， pp. 3051-3073

［2］ Arikan .E，―Channel polarization: a method for constructing capacity-achieving codes，” in Proc. ［J］ IEEE Int. Symp. Inf. Theory， Jul. 2008， pp. 1173-1177.

［3］ Arikan .E， “A performance comparison of polar codes and reed-muller codes，” ［J］ IEEE Communications Letters， 2008， vol. 12， no. 6， pp. 447-449.

［4］ Trifonov P.， ―Efficient design and decoding of polar codes，” ［J］ IEEE Trans. Commun.， Nov. 2012， vol. 60， no. 11， pp. 3221-3227.

［5］ Ryan W. and Lin S.， Channel Codes: Classical and Modern. ［M］New York， NY， USA: Cambridge Univ. Press，2009.

［6］ Chung S.， Thomas Richardson J.， and Urbanke R.，“Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation，” ［J］IEEE Transactions on Information Theory， Feb. 2001， vol. 47， no.2， pp. 657-670.

［7］ Tal I. and Vardy A.， ―How to construct polar codes，” ［J］IEEE Trans. Inf. Theory， 2013， vol. 59， no. 10， pp. 6562-6582.

［8］ Divsalar D.， Dolinar S.， Pollara F.，―I terative Turbo decoder analysis based on density evolution，” ［J］ IEEE J. Select. Areas Commun.， 2001: pp.891-907.

［9］ Chung S.， ―On the construction of some capacity-approa -ching coding schemes，” ［M］Ph. D. dissertation， Dept. Elect. Eng.， Mass. Inst. Technol.， Cambridge， MA，

［10］ Richardson T. and Urbanke R. ，― The capacity of low-density parity-check codes under message-passing decoding， ［J］”IEEE Trans. Inf. Theory， 2001， 47（2），pp.599-618..

［11］ Proakis J. G.， Digital Communications［M］. M cGraw Hill，1995.

Selection of Information Bit of Polar Code under AWGN Channel

Cui Yin，Ni Weiming （Department of Information Science and Technology， Fudan University， Shanghai 200433， China）

Abstract:The polar code， which has been popular among the channel coding area， is the first and the unique method that could be proved to construct capacity-achieving codes for any symmetric binary-input discrete memoryless channels. Based on the channel polarization， N copies of the channels can be divided into two parts， the noiseless channel and the pure noise channel. How to select the good channel has been of one the key points while applying the polar codes. At the same time， polar codes is sensitive to the type of channel， which determines that it will be different to choose the good channels when the type of the channel is different.

Key words:Polar Code； Channel Polarization； AWGN Channel； Information Bit

中图分类号：TN911.22

文献标志码：A

文章编号：1007-757X（2016）05-0068-05

作者简介：崔 茵（1991-），女，仙桃人，复旦大学，信息科学与工程学院，硕士研究生，研究方向：信道编码，上海，200433倪卫明（1970-），男，上海市人，复旦大学，信息科学与工程学院，副教授，博士，研究方向：无线通信和无线网、通信信号处理、编码技术，上海，200433

收稿日期:（2015.10.23）