无源定位跟踪中野值的检测与剔除方法

杨军玲

(西安电子科技大学 电子工程学院，陕西 西安 710071)

无源定位跟踪中野值的检测与剔除方法

杨军玲

(西安电子科技大学 电子工程学院，陕西 西安 710071)

摘要针对无源定位跟踪中野值的出现会降低滤波的可靠性和稳定性问题，结合新息似然的概念提出了一种基于似然的野值检测与剔除方法。通过计算卡尔曼滤波更新中得到的似然值，设定门限，以达到野值的检测与剔除的目的。仿真结果表明，该算法有效地处理了野值对定位跟踪精度的影响，使得目标定位跟踪精度有了较大的提高。

关键词定位跟踪；野值；新息似然；卡尔曼滤波

在无源定位跟踪[1]中，由于一些偶然因素，使得量测中出现错误量测值或野值[2]。野值的出现不仅影响当前时刻的滤波结果，同时会影响接下来的跟踪精度。所以，在无源定位与跟踪中，对于野值的检测和剔除研究尤为重要。

1野值对卡尔曼滤波的影响

卡尔曼滤波根据线性最小方差估计原理[3-4]，是无源定位跟踪的线性最优滤波器。当野值出现时，会严重影响卡尔曼滤波的滤波精度[5-7]。假设系统的状态方程和量测方程分别如下

(1)

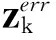
(2)

根据卡尔曼滤波公式可知，k时刻状态的滤波估计值为

(3)

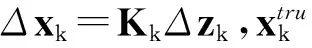
2常用的野值检测与剔除方法

野值的出现会严重影响滤波的结果，因此，对于野值的检测与剔除的研究具有重要意义。目前，有以下几种野值的判别方法。

2.1新息判别法一

假设 时刻的状态估计值为 ，根据卡尔曼滤波可得xk-1|k-1时刻的状态预测为

xk|k-1=Fxk-1|k-1

(4)

量测预测值为

zk|k-1=Hxk|k-1

(5)

新息为

(6)

为判断得到的观测值是否为野值，可用与之对应的量测预测与其进行比较[8]，即判定新息的范数大小，即

(7)

给Δzk设定一个门限T，当Δzk超过门限T时，则认为量测值zk是野值，并用状态预测xk|k-1来代替zk。若Δzk没有超过门限T，则认为量测值zk是正常的，并利用其进行滤波。即

(8)

其中

(9)

[Δxk|k-1,Δyk|k-1,Δzk|k-1,]=xk|k-1-xk-1|k-1

(10)

即将两次采样时间间隔内目标距离的增量的倍数作为判别门限。

系数K的经验取值在4～6之间[8]，此方法可有效地对量测中的野值进行检测与剔除。但是此方法是基于卡尔曼滤波处于稳态后才有效，当其处于过渡态，效果会有影响。

2.2新息判别法二

首先，求解新息协方差根

Ck=sqrt(Sk)

(11)

并根据式(12)来对增益矩阵进行控制

(12)

其中，m∈[0,1]，λ取经验值λ=3。此方法可通过新息来对卡尔曼滤波增益进行动态调整，从而达到了对野值的自适应检测与剔除。但当目标自身状态变化较大，则会误认为量测值非正常，从而影响滤波结果。

2.3新息判别法三

由于新息的统计特性与量测值的统计特性是一致的[10]，故当量测值中出现野值时，新息的统计特性将发生变化，所以可通过对新息的统计特性进行分析，并据此判断量测值是否为野值。

首先采用开窗估计法来估计信息协方差

(13)

其中，N为滑动采用区间

j0=n-N+1

(14)

正常情况下，信息协方差Sk与估计值相近，应该在1附近，若观测值是野值，则比值会偏离1，因此可通过式(15)进行判定

(15)

其中，ε是干扰量，表明工程应用中所能接受的极限误差。若两者的比值满足式(15)，则量测值zk不是野值，否则量测值zk被判定为野值，并对量测值进行如下的修正处理

(16)

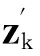
(17)

此方法可通过控制 的大小，可以自适应处理野值。但该方法同样要基于卡尔曼滤波处于稳态后才更有效，当其处于过渡态，效果会有影响。

3基于新息似然的野值检测与剔除

本文在卡尔曼滤波框架下，从似然函数的角度分析，对野值进行检测与剔除。假设 时刻的量测值是野值，则根据在卡尔曼滤波的更新过程中，其与量测预测值相差较大，如图1所示。即在未发生野值的情况下，正常的量测值应该在量测预测值附近，若出现野值，野值应在离量测预测值比较远的位置。

图1　量测分布图

图2　新息似然函数分布图

因此，本文根据新息的这一特点，提出了基于新息似然函数的野值判别法，来对野值进行检测与剔除。即在卡尔曼的更新过程中，求出新息似然的值，并进行判定，当其小于某一固定门限时，则认为量测值是野值，并进一步处理，从而达到对野值的检测及修正。

(18)

并对新息似然值进行如下判断

w<λ

(19)

其中，λ是判别门限，取经验值λ=0.004。若λ的取值太小，则会造成一部分野值无法被剔除，而λ的取值过大，则会误删除一部分合理信息。野值的检测与剔除是通过判定新息似然函数是否小于门限λ。正常情况下，新息为零均值高斯白噪声，且正常的量测值的新息似然函数值w会>λ。

假设k时刻式(19)成立，则认为k时刻出现了野值，并令此时的状态估计值zk=Hxk|k-1，再进行卡尔曼滤波。即野值的检测与剔除可表示为

(20)

因此，通过对新息似然函数的判断，本文所提算法便可有效地对野值进行检测与剔除，从而提高滤波精度。

4仿真实验与分析

为证明所提算法的有效性，将新息似然函数法与传统卡尔曼滤波算法进行比较。

应用式(1)的状态方程和观测方程建立目标运动模型，以二维平面做匀速直线运动为例。

图3　位置估计误差

图4　速度估计误差

图3和图4分别给出了两种算法的位置均方根误差和速度均方根误差。由图可知，由于普通卡尔曼滤波未对野值进行检测与剔除，所以其滤波性能相对较差，尤其是在野值出现的3个时刻，卡尔曼滤波的状态估计值明显偏离目标真实运动轨迹。而本文所提方法因采用了新息似然判别法对野值进行检测以及修正，具有良好的滤波结果。

5结束语

野值的出现会影响无源定位跟踪中的滤波精度。本文首先分析了野值对卡尔曼滤波性能的影响，并介绍了3种处理野值的滤波算法；结合似然函数概念，提出了基于新息似然函数的野值检测与剔除算法。仿真实验结果表明，本文所提算法能有效地对野值进行检测与剔除，提高了滤波精度。

参考文献

[1]孙仲康,周一宇,何黎星.单多基地有源无源定位技术[M].北京:国防工业出版社,1996.

[2]Anscombe F J.Rejection of outliers[J]. Technometrics,1960,2(2):123-147.

[3]朱元昌,赵福红.火控系统原理与分析[M]. 北京:兵器工业出版社,1994.

[4]张贤达.现代信号处理[M].北京:清华大学出版社,2002.

[5]周金明,费为银,高婷婷.观测数据野值剔除的TBS-LS逼近方法[J].飞行器测控学报,2012,31(1):71-74.

[6]黄鹤,张会生,黄莺,等.一种抗野值的 Kalman跟踪滤波器[J].微处理机,2009，30(2):51-53.

[7]柳海峰,姚郁,卢迪,等.Kalman滤波新息正交性抗野值法研究[J].电机与控制学报,2003,7(1): 40-42.

[8]孙书鹰,段修生,王志强,等.目标跟踪系统中野值的判别与剔除方法[J].火力与指挥控制,2004,29(6):85-87.

[9]王光鼎,张升康,杨汝良.一种基于卡尔曼滤波处理的北斗卫星无源组合导航自适应野值剔除方法[J].电子与信息学报,2008, 30(8):1981-1984.

[10]张强,孙红胜,胡泽明.目标跟踪中野值的判别与剔除方法[J].太赫兹科学与电子信息学报,2014,12(2):256-259.

Method of Detecting and Rejecting Outliers in Passive Locating and Tracking

YANGJunling

(SchoolofElectronicEngineering,XidianUnibersity,Xi'an710071,China)

AbstractIn passive locating and tracking system, the emergence of outlier has a bad influence in both the stability and the precision of the filtering. In order to solve this problem, a method for the outlier detection and elimination based the conception of innovation likelihood is proposed. Given a threshold, the innovation likelihood is calculated in the update of the Kalman filter to aim at the detection and elimination of the outlier. The proposed algorithm plays a good performance in passive locating and tracking system with outlier.

Keywordslocating and tracking；outlier；innovation likelihood；kalman filter

收稿日期:2015-10-23

作者简介:杨军玲(1984-)，女，硕士研究生。研究方向：无源定位与跟踪。

doi:10.16180/j.cnki.issn1007-7820.2016.06.015

中图分类号TN953

文献标识码A

文章编号1007-7820(2016)06-051-03