基于GBM模型的价差期权定价方法

陈宁娟

(西安电子科技大学 数学与统计学院，陕西 西安 710126)

基于GBM模型的价差期权定价方法

陈宁娟

(西安电子科技大学 数学与统计学院，陕西 西安 710126)

摘要假定交易不连续，基于历史信息、风险偏好中性和几何布朗运动，文中主要从价差期权实值执行边界的不同情况出发，以定理的形式给出了价差期权和数字价差期权价格公式的优化方法，并确立了价差期权价格公式的解析近似解的恰当形式。同时，还对实值执行边界的单调性和凹凸性给出了性质定理，这在一定程度上方便了价差期权和数字价差期权的定价公式研究。

关键词风险中性；闭形式解；执行边界

价差期权[1]允许投资者对两种或者两种以上的期权进行操作而从中获取利润，其在证券、固定收入、外贸交易和商品市场等方面相当流行。例如将精炼石油与原油之间的差价作为标的资产的价差期权就为炼油商提供了利用石油毛利进行套期保值的路径。还有一些交易者自创了新的价差期权形式，并不是以两种而是多种资产的价差作为标的资产的价差期权，由此就出现了涉及多种基础资产的价差期权。

本文主要的工作分为以下几部分：首先，对在几何布朗运动[2]模型下价差期权和数字价差期权，给出价格的总体表达式；为了计算总体表达式，以定理的形式给出化简总体表达式的工具；最后，给出几何布朗运动模型下，价差期权和数字价差期权价格的闭形式解。

1模型建立

在建立模型之前，先看一般假设，令两个基础资产的收益服从联合正态分布。当二者差价K=0时，交易期权的价格存在其所满足的隐式方程式。然而，一般情况下K≠0，其所满足的隐式方程式就不易得到。接下来，就一般情况给出其价格公式的解析近似解，且其相对误差小于万分之一(在这些期权的买卖价差观察范围内)。

当在t时，标记S1(t)和S1(t)为两个基础资产的价格，则在交割时刻T，价差期权的收益为[S1(T)-S2(T)-K]+，其中f+为f的正部。相应的数字价差期权的收益就为I{S1(T)-S2(T)-K≥0}，则

由风险中性定价方法可得出价差期权和数字价差期权的估价公式

V=erTEQ[S1(T)-S2(T)-K]+VD=

e-rTEQ[IS1(T)-S2(T)-K≥0]

(1)

其中，Q为风险中性测度；r为无风险利率，且在Q下标的资产的折现价格为鞅。

为计算这两个期权的价格，文中作出如下假设：假定logS1(T)log和S2(T)服从联合正态分布，且初始价格为S1(0)=S1，S2(0)=S2，并取

(2)

上述的期望和方差均为定值，所以定义

(3)

同时二者的联合分布是相关系数为ρ的正态分布函数，在测度Q下其边缘分布服从标准正态分布。

下面介绍本文的根基模型：几何布朗运动(GEM)模型。首先，几何布朗运动模型的价格满足关系

dSi(t)=(r-qi)Si(t)dt+σiSi(t)dWi(t)

(4)

(5)

接下来，文中对价差期权的执行范围做如下分析。价差期权的边界以logSi(T)的最小值为定义，且其是logS2(T)的函数，二者均是实值执行的期权。需要注意的是，当K=0，执行边界是一次函数形式，即满足线性，而此时期权价格有解析解。当K≠0，由于边界的非线性而不容易获得结果。

在执行时刻T，当S1(T)-S2(T)-K≥0时，期权为实值交易。设K≥0，则由(5)式可知，实值交易的条件可变形为

(6)

所以，令等式右边为

(7)

在式(7)中令Y=y，则当X≥x(y)时，期权进行实值交割。当K<0时，会有ev2Y+μ2+K<0的情况出现，因此式(6)中的条件不总是成立。所以文中给其进行形式转换

[S1(T)-S2(T)-K]+=S1(T)-S2(T)-

K+[S2(T)-S1(T)-K]+

(8)

由此就能将出现的不利情况有利化。所以，当出现K<0的情况时，可转化为K≥0的情况来计算VD和V。

2价差期权公式解析解的优化

文中式(1)给出了两个期权组合的宏观表达式，下面将其优化，Pearson L[3]给出了一种将二维积分转化为一维积分的方法，该方法不仅对期权价格的解析解计算较有用处，且对数值方法同样有用。

定理1 假设收益是联合正态分布[4]的，则式(1)还可进一步表示如下

(9)

(10)

其中，n(·)和N(·)分别为标准正态密度函数和标准正态累积分布函数。同时可定义

(11)

定理1中的式(9)给出的表达式类似于Black-Scholes公式。通常，认为A(y)和Black-Scholes[2]表达式中的d2为同一个角色。所以，称A(y)为价差期权的条件价值状况[3]。N(A(y))为风险中性概率测度，且当Y取y值时，价差期权为实值执行。表示如下

N(A(y))=ProbQ[S1(T)≥S2(T)+K|Y=

(12)

与Black-Scholes公式不同，本文中的 是一个服从标准正态分布的随机变量。对于一般的计价单位方法[5]的变化情况，本文不作讨论。

对定理1继续延伸，给出定理2。当K=0时，定理2用建立数学恒等式的方式推导出了Margrabe[6]方程式。Li[7]和Zhou[8]在2008年就指出，若将n(y;μ,σ2)看作logS2(T)的密度函数，a+by看作条件价值状况，则当A(y)为y的线性函数时，这个密度函数就变为无条件的价值状况，还可在闭形式下解出来。当收益服从联合正态分布(仅对GBM模型)时，文中给出的Margrabe[5]方程式比初始偏微分方程在所有模型中的应用更为广泛。

定理2设a,b∈R，则

(13)

当K=0，条件价值状况A(y)是y的线性函数。因此，由式(13)可知，交易期权的价格在假设收益体系下由下面的Margrabe方程式给出

(14)

图1　执行边界

图1展示了在不同的K值下执行边界函数x(y)的图像,各参数取值如表1所示。

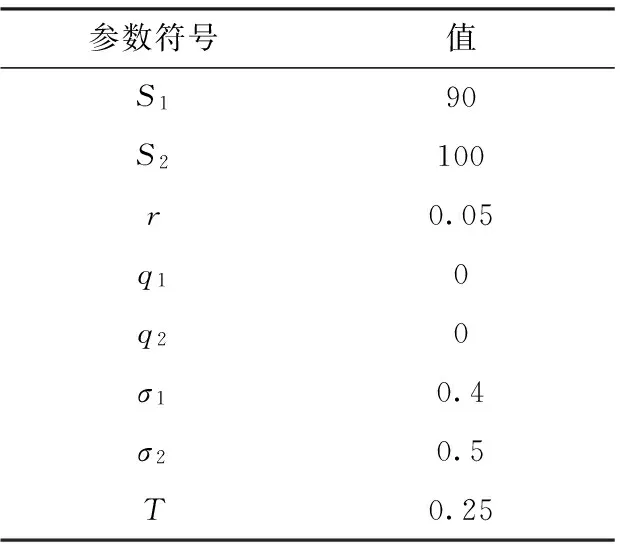
表1　各个参数的取值

文中用低阶的泰勒展开式逼近x(y)，比如用一次函数或二次函数，这点对Ji的逼近均各有优势。注意到，在K=0和σ2=0时，x(y)均为线性函数，因此在这种思想下，文中的逼近均有效。这也揭示了当σ2=0时，估价公式就会退化为Black-Scholes方程；当K=0时，却会变为交易期权的Margrabe方程式。图2说明了当y→0时A(y)的变化情况。

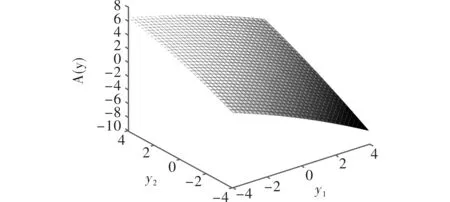
图2　当y→0时的A(y)

接下来，通过定理3给出x(y)、A(y)和N(A(y))的单调性、凹凸性以及在所满足的不同条件下所呈现的相应情况。

定理3K≥0令|ρ<1|，则有：

(1)执行边界x(y)是y的增、凸函数;

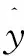
(3)条件价值状况A(y)为y的凹函数;

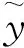
3价格闭形式解

当K=0时，可计算相应分量。因此，纯几何布朗运动模型下的数字价差期权和价差期权的价格公式为

(15)

(16)

其中，S11=S1eq1T，S22=S2eq2T。

4结束语

当下，尽管这种涉及多种基础资产的价差期权应用范围有限，但随着交易市场的日益完善、风险管理的日益完整以及全球资本市场一体化的飞速发展，这种多元化的价差期权将会成为人们普通使用的金融衍生品工具。

参考文献

[1]孙健.金融衍生品定价模型:数理金融引论[M].北京:中国经济出版社,2007.

[2]Black F, Scholes M. The pricing of options and corporate liabilities[J].Journal of Political Economy, 1973,81(3):637-659.

[3]Pearson N. An efficient approach for pricing spread options[J].Journal of Derivatives,1999，3(1):76-91.

[4]Zhou Jieyun.Real options valuation in energy markets[D].Atlanta：Ceorgva lnstitute of Technology,2010.

[5]Geman H,N E Karoui,J C Rochet. Changes of numeriaire changes of probalitity measure and option pricing[J].Journal of Applied Probability,1995,32(2):443-458.

[6]Margrabe W.The value of an option to exchange one asset for another[J].Journal of Finance,1978(33):177-176.

[7]Li M,Deng S J,Zhou J.Closed-form approximations for spread option prices and Greeks[J].Journal of Derivatives,2008,15(3):58-80.

[8]Li M,Deng S J,Zhou J.Multi-assets spread option pricing and hedging[J].Quantitative Finance Quantitative,2010,10(3):305-324.

Spread Options Pricing Methods Based on Geometric Brownian Motion Model

CHEN Ningjuan

(School of Mathematics and Statistics，Xidian University, Xi’an 710126, China)

AbstractOption pricing plays an important role in financial mathematics research.Spread option is application and popularization of options.Assumes transactions are not continuous,based on historical information and risk-neutral preference and the Geometric Brownian motion as a reference model and taking different exercise boundaries in the money into consideration,the pricing optimization methods for spread option and digital spread option are introduced.Finally, the appropriate and closed-form formula for spread option and digital spread option is established.Furthermore, the monotonicity and convexity theorems of exercise boundary in the money is given,which facilitates the spread option and digital spread option pricing formula to a certain extent.

Keywordsrisk-neutral；closed-form formula；exercise boundary

收稿日期:2015-10-16

作者简介:陈宁娟(1989-)，女，硕士研究生。研究方向：随机过程与金融风险计算。

doi:10.16180/j.cnki.issn1007-7820.2016.06.017

中图分类号F830.59；O21

文献标识码A

文章编号1007-7820(2016)06-058-03