一种基于一阶差分的野值类型判别及处理方法1

饶云峰，白燕，3

一种基于一阶差分的野值类型判别及处理方法1

饶云峰1，2，白燕1，2，3

（1.中国科学院 国家授时中心，西安 710600；2.中国科学院大学，北京 100049；3.中国科学院 精密导航定位与定时技术重点实验室，西安 710600）

为了剔除违反规律的异常测量值，采用一种基于一阶差分的野值类型判别及处理方法。仿真结果表明，该算法能准确地判别野值类型及其位置，尤其是对于斑点型野值具有较好的效果，同时可以提高数据处理精度，缩短数据处理时间。

斑点型野值；散点型野值；一阶差分；判别和修正

0　引言

测量设备记录的测量数据往往包含较大的随机误差，个别值可能与其他值截然不同，违反了数据的整体变化规律，这些异常测量值就是野值[1]。工程测量中不可避免地存在野值，其对测量精度和数据处理的结果都会带来严重的影响[2]，在数据处理过程中必须对这这些违反测量规律的野值进行修正和剔除。野值的表现形式主要有以下2种[3]：

①散点型野值：野值以孤立点的形式出现。具体表现是：i时刻的观测数据为野值，而在包含i时刻的某一时段内其他观测数据是正常的。

②斑点型野值：因相关性影响，野值成片出现，若i时刻的观测数据为野值，其后一段时间内的值或绝大部分值也是异常的。

野值点的成因、野值类型、野值模型等可参见文献[1]～[3]。野值类型不同，剔除方法也不同。很多野值识别或剔除方法实现起来较复杂，如文献[1]～[6]中提到的方法；有些方法只对散点型野值有很好的处理结果，而对斑点型野值的处理结果却并不是很理想，如文献[7]中提到的统计学方法和一些非统计学方法（Tukey53H法和灰自助法）、文献[8]中提到的相位空间法。文献[7]～[8]中提到的方法能很好地剔除散点型野值，而对于斑点型野值就很难剔除，尤其是文献[8]中提到的相位空间法，它能很好地剔除散点型野值，且相比于其他野值剔除算法其最大优势是不需要设定门限值[7-8]，但当工程实践中的测量数据出现大量斑点型野值时，即使多次利用相位空间法也无法剔除斑点型野值。为了解决此问题，本文提出一种基于一阶差分的野值类型判别及处理方法。该方法可以判别数据中是否存在斑点型野值，精确找出斑点型野值在原始数据中的位置并加以剔除。

1　野值类型判别及处理算法

1.1野值类型判别算法

当测量数据中存在野值，则该数据序列的一阶差分序列会出现明显的函数跳跃点（通过与经验阈值比较后确定是否为跳跃点）。若出现单点跳跃点，表明此点前后数据中至少有一段数据是斑点型野值；若出现连续2个以上的跳跃点，表明这段连续跳跃点的第一个和最后一个跳跃点的前后数据中至少有一段数据是斑点型野值；若仅出现2个连续的跳跃点，表明原始数据中对应2跳跃点后者的点为散点。这些跳跃点把原始数据分成若干数据段和散点型野值点，求每段数据的均值，并将得到的均值与对应拟合数据段的均值进行比较，两者之差超过经验阈值的这段数据即为斑点型野值。这样就确定了野值类型及野值在原始数据中的位置。设原始数据序列为 u（i），1≤i≤n，n为原始测量数据的总长度。判断原始数据中野值类型及位置的具体步骤如下：

①求 u（i）的一阶差分：Δu（i）=u（i+1）-u（i），1≤i≤n；

③散点型野值类型判断：若Mark中的某段相邻元素有且只有2个元素值是连续的，则后一个元素对应的原始数据为散点型野值；

④数据分段：根据Mark中相邻元素值是否连续，可将原始数据分段。具体分段方法为：当Mark中某个元素的值与其后一个元素的值不连续时，取该元素加入数列End；当Mark中某段元素仅有2个值连续时，取前一个元素加入End，后一个元素作为散点型野值点；当Mark中某段元素有2个以上的值连续时，取该段连续值的第一个元素和最后一个元素加入End；另外将原始数据的最后一个数据点的序数也作为最后一个元素加入End；所构成的数列End的长度为m，此时就将原始数据分为了m段。对于Mark中仅有2个值连续的情况，若放入End的元素对应为End（j），则其对应的第j+1段数据的起点为End（j）+2，终点为End（j+1）；其余情况时，若第j个数据段的终止点为End（j），起始点为End（j -1）+1；另外对于第一个数据段，其终止点为End中的第一个元素，起始点为原始数据的第一个数据；

⑥对判断出的野值进行修正。

通过上述步骤①～⑤就可识别出原始数据中的斑点型野值和散点型野值，并精确定位其在原始数据中的位置。

1.2野值修正

在进行野值修正时，若原始数据量大，则可直接剔除野值点，但这样会导致数据的不连续；也可将野值用一定值替代，其他正常值保持不变。一般有以下几种替代方法[8]：

④拟合值；

⑤根据野值两端的数值做插值。

对于静态数据（无运动趋势的测量数据），上述5种野值替代的方法都可使用，但对于动态数据（数据有明显的运动趋势），方法①～③反而会使数据处理精度变得更差，所以对于动态数据可使用方法④～⑤进行野值修正，也可以把动态数据的运动趋势去除[9]后，再用上述5种方法中的任意一种替代野值，野值剔除后再把该运动趋势加回至剔除野值后的数据中。当野值对整体数据影响比较大时，可多次使用本文提出的野值判别及修正方法，直至数据中无明显的粗大值。

2　数据处理及结果分析

2.1仿真数据处理

为了进一步说明不同类型的野值判别方法，模拟仿真了一组带有白噪声的数据，其长度n=1000，均值为500，在此基础上将点80，150，500，760改为散点型野值，点[20，35]，[255，285]改为斑点型野值，野值总数为51，占总数据的5.1%，记该组仿真数据为data。仿真数据data如图1所示。

图1原始数据

对原始数据data求一阶差分，一阶差分的绝对值与阈值1R比较，得到一阶差分函数中的跳跃点。本文设跳跃点的判决阈值113Rσ=，1σ为一阶差分的标准方差。原始数据的一阶差分如图2所示。图2中，实线代表原始数据的一阶差分，虚线代表跳跃点的判决阈值。

图2　原始数据的一阶差分及其阈值

图3为2种类型野值的一阶差分局部放大图，由于篇幅限制，此处只给出其中2段存在野值的数据（19，35），（499，500）的情况。一阶差分与阈值1R比较，跳跃点的位置为Mark={19，35，79，80，149，150，254，285，499，500，759，760}，其中[79，80]，[149，150]，[499，500]，[759，760]是2个连续跳跃的点（图3（b）所示），根据2.1节中的步骤③可知，原始数据data中的点80，150，500，760为散点型野值。一阶差分在点19，35，254，285处为单个的跳跃点（图3（a）所示），由步骤④可得，原始数据被分为[1，19]，[20，35]，[36，79]，[81，149]，[151，254]，[255，285]，[286，499]，[501，759]，[761，1000]9段数据和散点80，150，500，760，需进一步对数据组判断，判断其是否为斑点型的野值。

图3　一阶差分对应野值的局部放大图

根据步骤⑤判断上述9段数据是否为斑点型野值，设斑点型野值判决阈值为各数据段的均值减去对应拟合数据段的均值的标准方差，即为求标准方差函数。经过比较，只有数据组[20，35]，[255，285]满足条件，所以数据组[20，35]，[255，285]为斑点型野值。

综上可得，点80，150，500，760被识别为散点型野值，数据组[20，35]，[255，285]被识别为斑点型野值，该判别结果与仿真数据中的野值类型及位置一致。

由于该组仿真数据为静态数据，所以这里用原始数据的均值代替野值，其他数据保持不变。野值修正结果如图4所示。

图4　原始数据与野值剔除结果比较图

图4中，实线代表原始数据，带“*”的曲线为使用一次本文提出算法的数据处理结果。从图中可以看出，[20，35]，[255，285]中的斑点型野值被完全修正，点80，150，500，760处的散点型野值也被完全修正。所以本文提出的算法能准确判别野值类型，并精确定位野值在原始数据中的位置。

2.2实测数据处理结果

为了验证本文提出的算法的可行性和有效性，将本文提出的算法应用于处理一组实际无线环境中的测距数据，并将经过该算法处理后的数据与原始数据进行比较。同时利用本文提出的算法与相位空间法分别对该组实测数据进行处理，并比较2种算法对于测距精度的影响。

1）基于一阶差分的野值类型判别及处理结果

图5为中国科学院国家授时中心2015年1月的某次无线综合试验中一组伪距测量原始数据。从图5可知，该段测量数据在点（250，410）之间明显包含数段斑点型野值，整段数据中也包含一些散点型野值。根据2.1节所述步骤对该组数据进行处理，取为一阶差分的标准方差；σ2为所分数据段的均值减去对应段拟合数据的均值的标准方差，即，野值用6阶最小二乘拟合值代替。

图6给出利用本文提出的算法对野值进行修正后的结果，实线代表原始数据，带“*”的曲线表示本文提出的算法的数据处理结果。从图中可以看出，原始数据中的点（250，410）内的野值被完全修正，处理结果达到了预期的目的。

图5　实测原始数据

图6　基于一阶差分的野值类型判别及处理方法

2）相位空间法野值修正结果

相位空间法[8]：以原始数据 u（i）的残差及原始数据的二阶导为轴画一个椭圆，其中，的一阶导。若数据点在椭圆外，则判为野值，用修正值代替；若数据点在椭圆内，则判为正常的测量数据，不处理。

为了与基于一阶差分的野值类型判别及处理方法比较，此方法中的野值也用6阶最小二乘拟合值代替。

图7为循环使用相位空间法4次修正后的数据，实线代表原始数据，带“o”的曲线代表循环使用相位空间法4次的野值剔除结果。对该组数据，循环使用相位空间法4次后，所有的数据都满足在椭圆内的条件，即该组数据最多只能循环使用相位空间法4次。从图中可以看出，原始数据中的点（250，410）内的斑点型野值只有部分被修正，处理结果并不是很理想，但数据中的部分散点型野值得到相应的修正。

图7　循环使用相位空间法4次修正后的数据

3）2种方法的比较

图8给出了采用2种方法处理后的数据与原始数据的比对结果，实线代表原始数据，带“o”的曲线代表循环使用相位空间法4次的野值剔除结果，带“*”的曲线代表本文提出的算法的数据处理结果。从图中可以看出，2种方法都能修正数据中的散点型野值，但是对（250，410）区间内的斑点型野值，相位空间法处理结果并不是很好，而采用本文提出的方法能判断出该部分的斑点型野值并能很好地修正该部分斑点型野值。

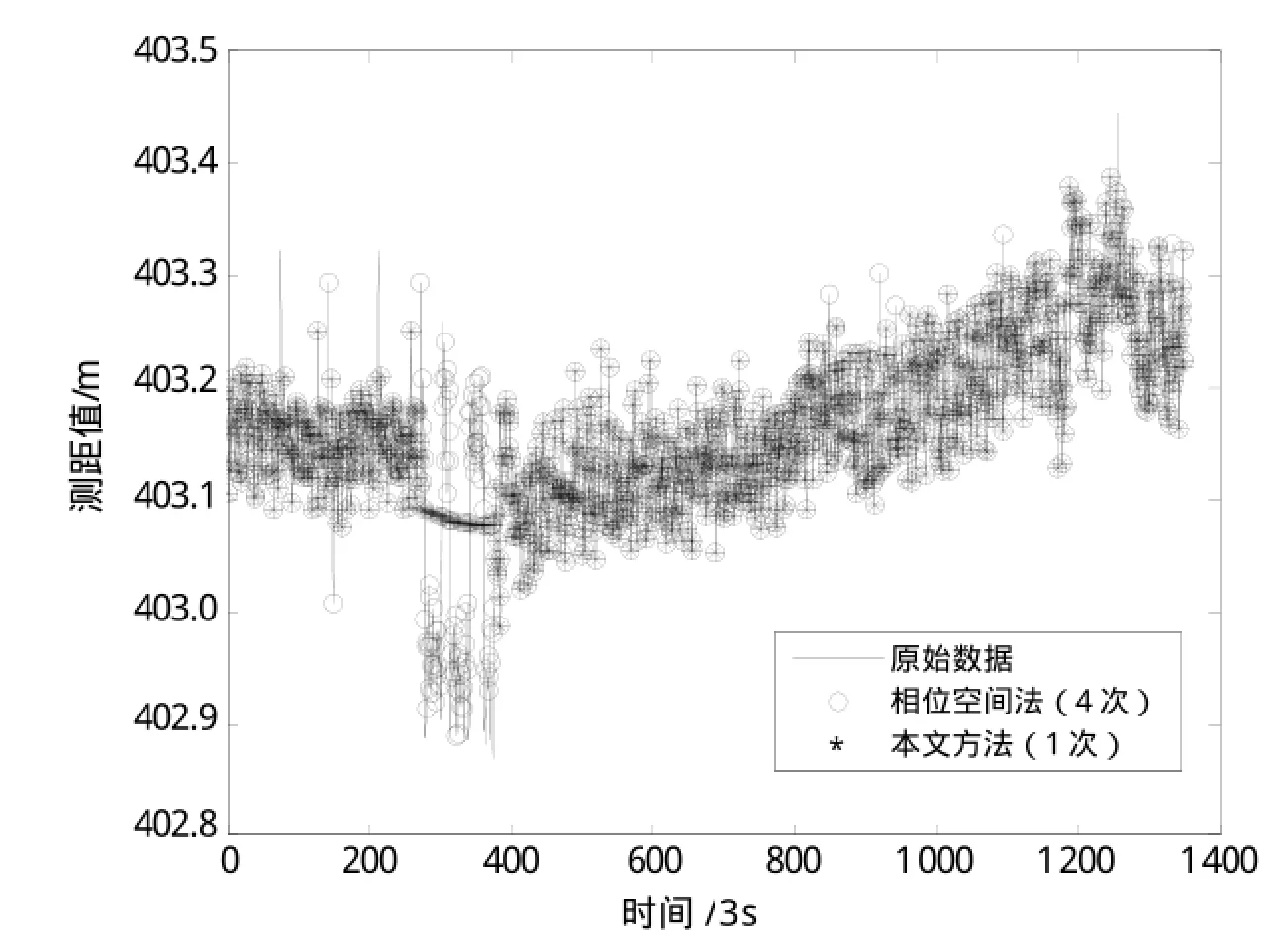
图8　2种方法处理结果与原始数据的比较

另外，不同的数据处理方法对测量数据的精度会产生不同的影响。对采用上述2种算法进行处理后的数据分别求取其均值和标准方差，结果如表1所示。从表中可看出，采用2种算法分别对该组数据进行预处理后再求其测距精度，相比对没有经过处理的原始数据直接求得的测距精度，均有明显提高；另外，当处理次数相同（1次）的情况下，经过本文提出的算法处理后求得的测距精度要比经过相位空间法处理后的测距精度高出0.0115；即使循环使用4次相位空间法，其野值修正后的测距精度也没有使用本文算法（1次）后得到的测距精度高。因此，本文提出的算法在处理速度上要快于相位空间法，且数据处理后的精度也明显优于相位空间法。

表 1　实测数据的处理结果

3　结论

野值的判别及剔除是测量数据处理过程中非常重要的一个环节，本文提出了一种基于一阶差分的野值类型判别及处理方法，该方法能准确判别数据中的野值类型及其在原数据中的位置，相比相位空间法，该算法具有更高的数据处理精度和数据处理速度，可为有关工程实践中的数据处理提供一定的参考。

[1]黄家贵,吕红宁,王安丽.斑点型野值的进一步识别与处理[J].装备指挥技术学院学报,2002,13(6):56-59.

[2]胡绍林,孙国基.靶场外测数据野值点的统计诊断技术[J].宇航学报,1999,20(2):68-73.

[3]祝转明,秋宏兴,李济生,等.动态测量数据野值的辨识与剔除[J].系统工程与电子技术,2004,26(2):147-149,190.

[4]胡峰,孙国基.Kalman滤波的抗野值修正[J].自动化学报,1999,25(5):694-695.

[5]王佳,王敏,徐晓辉.一种干涉仪数据斑点型野值修正方法[J].弹箭与制导学报,2013,33(2):106-108.

[6]卓宁.靶场外弹道数据处理中野值点剔除方法[J].测试技术学报,2008,22(4):313-317.

[7]杨筱.卫星导航系统数据与信号质量评估技术研究[D].长沙:国防科学技术大学,2009.

[8]GORING D G.NIKORA V I.Despiking acoustic doppler velocimeter data[J].Journal of Hydraulic Engineering,2002,128(1): 117-126.

[9]BAHAER.趋势项提取+莱特准则的野值剔除方法[EB/OL].(2010-10-10)[2015-01-13].http://blog.sina.com.cn/s/blog_5de f5a660100m3mr.html.

Amethod based on first-order difference for type-judging and processing of outliers

RAO Yun-feng1，2，BAI Yan1，2，3
（1.National Time Service Center，ChineseAcademy of Sciences，Xi′an 710600，China；2.University of ChineseAcademy of Sciences，Beijing 100049，China；3.Key Laboratory of Precision Navigation and Timing Technology，National Time Service Center，ChineseAcademy of Sciences，Xi′an 710600，China）

For eliminating the abnormal measured values，a method based on the first-order difference is adopted for judging the types of the outliers and processing them.The simulation results show that the type of outliers can be accurately differentiated and the location of outliers in the original data can be precisely pinpointed by using this algorithm，especially for the spotted outliers the processing result is rather good.At the same time，processing precision can be improved and the processing time can be reduced.

spotted outliers；isolated outliers；first-order difference；differentiation and correction

TP274

A

1674-0637（2015）04-0227-08

10.13875/j.issn.1674-0637.2015-04-0227-08

2015-06-25

国家自然科学基金资助项目（11203027）

饶云峰，女，硕士研究生，主要从事Ka频段星间链路信号质量性能评估方法的研究。