基于混合遗传算法的协同制造系统调度研究

任乃飞，于　璐

(江苏大学 机械工程学院，江苏 镇江 212000)

基于混合遗传算法的协同制造系统调度研究

任乃飞，于璐

(江苏大学 机械工程学院，江苏 镇江 212000)

摘要研究由多个加工站、一个集中物料存储区和一台自动引导小车(AGV)组成的协同制造系统调度问题。针对该调度问题，建立了工件和AGV调度集成的数学模型。提出一种改进的混合遗传算法，在标准遗传算法的基础上引入模拟退火算法的Boltzmann生存机制，加快了算法收敛速度，克服了遗传算法过早收敛的缺陷，同时对算法的变异、交叉算子和更新机制进行了改进。仿真实验表明，改进的混合遗传算法能有效优化作业顺序和AGV行走路径，为具有AGV约束的柔性生产调度提供一种有效的实践途径。

关键词混合遗传算法；自动引导小车；生产调度；协同制造系统；计算机仿真

随着人们对多品种小批量产品的需求急剧增加，而传统的大批量生产模式已不再满足此类需求。因此，适合多品种生产的协同制造系统(Collaborative Manufacturing System，CMS)逐渐成为制造业的重要生产模式。自动引导小车(Automatic Guided Vehicle，AGV)作为协同制造系统的一部分，其主要功能是搬运工件，按照不同顺序执行任务，对系统的运行效率会有较大影响。因此，在协同制造系统中需要采用高效的调度算法对AGV和工件进行综合调度，以此优化作业顺序和AGV任务执行顺序。这对节省制造成本、缩短生产周期和提高系统生产效率具有重要意义。

目前，国内外对AGV应用于实际生产的相关研究主要集中在算法对AGV全局路径的优化和多AGV调度等方面[1]。但建立起AGV调度与工件调度相集成的调度模型，并采用智能算法进行调度优化的研究较少。文献[2]对静态环境下的AGV行走路径进行建模，并采用遗传算法对该模型进行路径规划。文献[3]通过比较遗传算子的性能，最终得到了AGV路径规划的优化参数。文献[4]建立了复杂约束的AGV多参数问题数学模型，采用混合遗传算法优化了调度总时间。文献[5]针对多AGV系统，提出了一种基于阶段控制策略的分布式控制算法，有效提高了多AGV系统的工作稳定性。

本文对具有单AGV约束的协同制造系统调度问题进行分析，建立了该问题的优化模型，实现了工件与单AGV的集成化调度。针对标准遗传算法的不足，采用了将模拟退火算法中的Boltzmann生存机制引入遗传算法的遗传、交叉操作的结合方式，以此控制子代染色体的选择，并对标准遗传算法的交叉、变异算子进行改进。

1问题描述

协同制造系统的车间调度问题描述：n个工件在f台设备上完成加工，每个工件都有j道工序。各工序的加工时间和加工次序已知。加工过程中有一台AGV小车进行工件搬运任务。调度目标为：确定每台加工设备上的加工工件排序和每道工序的初始加工时间，使系统的最大完工时间(Makespan)最小。

该调度问题包含的约束条件如下：(1)在零时刻，各加工设备都可用，物料存储区的所有工件都可被加工；(2)开始加工之前，AGV小车停靠在物料存储区；当AGV完成当前搬运任务时，就停靠在刚执行完任务的加工站旁，等待下一个任务的开始；(3)同一时刻，每台设备仅能加工一个工件，且一旦开始就不可中断；(4)工件每道工序的加工时间已确定，且每道工序的开始和结束均会有安装和卸载时间；(5)AGV小车一次只能搬运一个工件；(6)AGV的行走速度为匀速，且在每台加工设备上的安装时间和卸载时间相同。

此外，假设AGV每一次搬运任务定义为如下4个步骤：从AGV当前位置移动到待装载位置；装载工件；AGV移动到待卸载位置；卸载工件。

2数学模型的建立

在数学模型中，符号定义如表1所示。

表1　符号说明

按照调度问题的描述，建立如下数学模型：

目标函数： min{max(Cij)}

s.t.Si0=0,∀i

(1)

(2)

(3)

(4)

Cij=Sij+Tij,∀i,j

(5)

Si(j+1)≥Cij,∀i,j

(6)

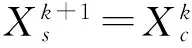
(7)

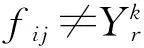
当工序O(i,j)的目标加工设备未被占用时，即

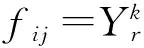
(10)

目标函数为最小化的最大完工时间；式(1)和式(2)表示设定系统的加工初始时刻为0；式(3)和式(4)分别表示AGV初始停靠位置和物料存储位置都在物料存储区；式(5)表示工序O(i,j)的完工时间；式(6)表示工件i的下一道工序必须在前一道工序完成之后进行，即工序一旦开始，不得中断；式(7)表示AGV的第K+1项搬运任务紧跟于AGV上一项搬运任务；式(8)和式(9)表示，当目标加工设备上存在未完工工件时，AGV的当前搬运任务的完成时间和O(i,j)的完工时间；式(10)表示，当目标加工设备未被占用时，AGV的当前搬运任务的完成时间和O(i,j)的完工时间。

3混合遗传算法的模型求解

遗传算法是在生物进化理论的基础上，通过自然选择和适者生存的进化机制来求解优化问题[6]。针对本文协同制造系统调度问题的求解，恰好可利用其良好的全局搜索能力，在较大规模的解空间中搜索最优解[7]。但遗传算法存在早熟、局部搜索能力差等不足[8]。而模拟退火算法可通过其概率突跳性的特点，在解空间中快速找到最优解，从而避免出现局部最优解[9]。模拟退火算法虽能较大程度地保证所得解为全局最优解，但算法的收敛速度较为缓慢。

综合遗传算法和模拟退火算法的优点和不足，本文将模拟退火算法中的Boltzmann生存机制引入标准遗传算法，并设计出两种算法的结合方式，使得改进的混合遗传算法克服了标准遗传算法易于早熟的缺点，从而提高了算法全局搜索的效率。

3.1改进的算法流程

混合遗传算法首先通过遗传算法进行种群进化，再通过模拟退火算法对产生的新解进行接受，算法基本步骤如下：(1)设置算法参数;(2)进行编码，随机产生初始种群;(3)设计易于实现的适应度函数，以评估每个个体的适应度值;(4)根据适应度值排列并选择个体，记录适应度值最高的个体;(5)根据交叉概率，进行交叉操作，并采用模拟退火算法的Boltzmann生存机制决定是否接受交叉后的新个体;(6)根据变异概率，进行变异操作，并采用模拟退火算法的Boltzmann生存机制决定是否接受交叉后的新个体;(7)进化次数k=k+1，进行降温操作tk+1=λtk;(8)判断是否达到终止条件，如果达到终止条件，转(9)；否则转(3);(9)输出最优解。

3.2编码和解码方式

基于工序的编码方法[10]可描述为：在染色体中，每个工件的工序都采用该工件的工件编号表示，某工件编号在染色体序列中第r次出现则代表该工件的第r道工序。例如：染色体为[323121321]，其中工件编号为3的基因在染色体中第2次出现，则表示这是3号工件的第2道工序。

染色体解码过程：根据染色体中每个基因位的信息，确定每台加工设备上的工件加工顺序和每道工序的加工起始时间、加工结束时间[11]。依据每道工序的加工起始时间，按照升序排列基因。AGV依据重新排列后的基因顺序进行运输服务，实现AGV调度的优化。

3.3适应度函数设计

适应度函数设计为

f=1/Makespan

(11)

式中Makespan为最大完工时间；由于目标函数是求解最小的最大完工时间。因此，要使得目标函数越小，适应度值应越大。适应度值越大，则该染色体被选择的几率越大。

3.4选择、交叉、变异算子

选择操作采用轮盘赌赋值法与精英策略相结合的选择算子。首先按照轮盘赌赋值法，计算所有个体的适应度值，个体适应度值越高，则被选入下一代种群的概率越大。找出当前群体中适应度值最高的个体Pmax和适应度值最低的个体Pmin，若迄今为止群体的最佳个体PBEST的适应度值高于Pmax，就用Pbest替代Pmin；若Pmax的适应度值高于Pbest，则用Pmax取代Pbest。

为保证算法产生染色体的多样性，这里采用线性交叉方式。交叉过程如图1描述如下：按照交叉概率随机选取待交叉染色体parent1和parent2，在两条染色体中随机选择两个对应交叉点，将两交叉点之间的基因段进行交叉；交叉完毕后，分别找出parent1和parent2中未交叉部分的基因段，依次记为a1和a2，将a1和a2分别按照其原来在parent2和parent1中的顺序，依次填入parent2和parent1中的未交换位置，就得到了子代染色体son2和son1。

变异操作能使搜索过程摆脱局部最优解，从而保证了算法的有效性。变异方式为：选取染色体上的一定长度基因段，对基因段上的基因进行逆序排列。该方式既增加了解的多样性，又不影响解的可行性。

3.5新解的接受机制

在标准遗传算法的交叉和变异算子中引入Boltzmann生存机制：设新产生的染色体的适应度值为f′，旧染色体的适应度值为f，二者的差值Δf=f′-f。根据概率

(12)

对新个体进行接受选择,其中，Tk为模拟退火温度冷却参数。

3.6终止条件

算法终止条件预设为最大进化代数N，当进化代数达到N时，迭代停止，输出最优解。

4仿真实验结果和分析

4.1实验条件

仿真实验是基于本校数字化设备研究所现有的协同制造系统进行的。该系统由4个加工站(编号为1～4，每个加工站各有一台加工设备)，一台AGV小车和一个立体仓库(编号为0)组成，布局如图2所示。整个系统有立体仓库一个公共缓冲区。实验采用4种不同类型的工件，每种工件都具有4道加工工序。这4种工件每道工序的加工时间矩阵Tx和加工设备矩阵Fx如下所示，T(i,j)表示第i种工件的第j道工序的加工时间，F(i,j)表示第i种工件的第j道工序的加工设备编号。AGV运输时间和动作集合如表2和表3所示。AGV卸载与装载时间均为5 s。

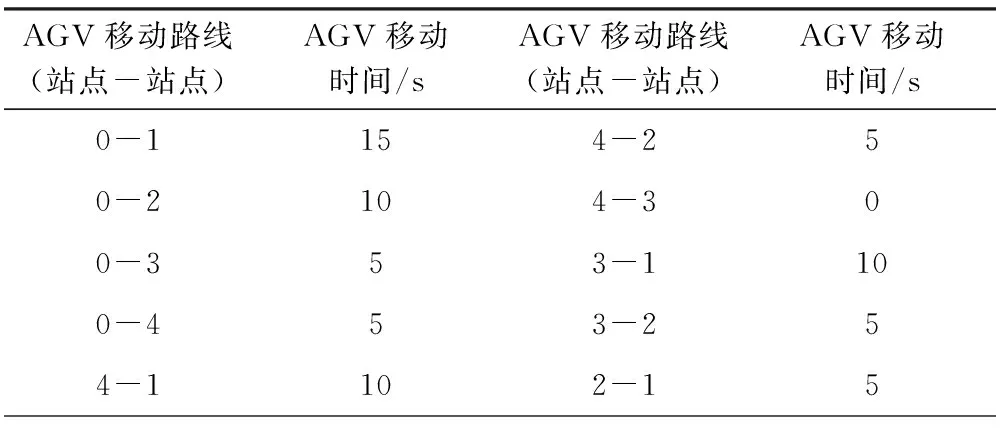
AGV移动路线(站点-站点)AGV移动时间/sAGV移动路线(站点-站点)AGV移动时间/s0-1154-250-2104-300-353-1100-453-254-1102-15

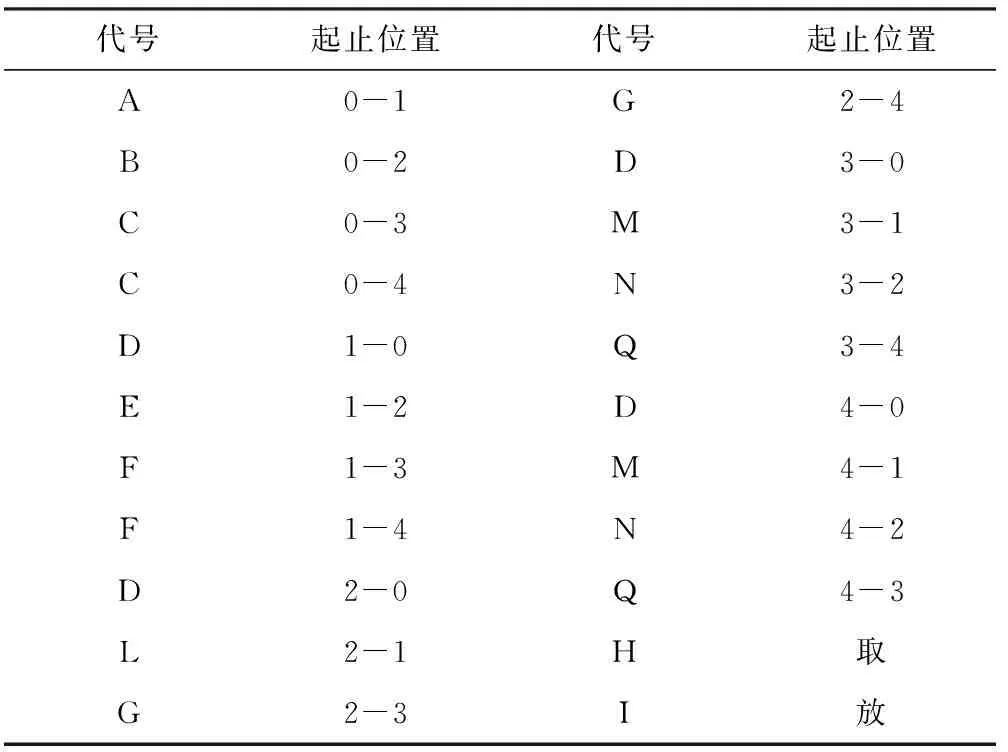
表3　AGV动作集合

4.2实验结果与分析

仿真实验中，分别采用前述改进的混合遗传算法和标准遗传算法来搜索最优解。算法参数取种群规模为100，交叉概率Pc为0.8，变异概率Pm为0.01，最大进化代数N为50。冷却系数λ=0.9，初始温度T0=1/2 000。

仿真实验获得8个工件进行加工的最佳调度甘特图如图3所示，甘特图中横坐标表示加工站，纵坐标表示加工时间。不同颜色的矩形代表不同工件的每道工序，矩形上的数字代表工件号。图中黑色曲线表示AGV工作时所处位置与动作持续时间的对应关系。

应用混合遗传算法时，最佳调度方案甘特图如图3(a)所示。系统的总加工时间为1 900 s，设备的总工作时间为1 310 s，AGV的行走序列为：H-B-I-D-H-C-I-D-H-A-I-D-H-C-I-N-H-D-I-C-H-D-I-H-C-I-D-H-B-I-G-H-D-I-H-C-I-M-H-D-I-H-A-I-F-H-D-I-B-H-D-I-H-B-I-D-H-C-I-Q-H-D-I-A-H-F-I-D-H-A-I-E-H-D-I-C-H-D-I-H-C-I-D-H-B-I-G-H-D-I-H-C-I-M-H-D-I-C-H-M-I-E-H-G-I-D-H-B-I-G-H-D-I-A-H-F-I-Q-H-M-I-D-H-C-I-N-H-D-I-H-B-I-L-H-D-I-H-A-I-F-H-D-I-H-C-I-Q-H-D-I-A-H-D-I-H-A-I-E-H-G-I-D-H-B-I-G-H-D-I-H-C-I-Q-H-D-I-H-C-I-M-H-D-I-H-A-I-E-H-D-I-C-H-D-I-H-C-I-D-H-B-I-L-H-D-I-C-H-D-I-B-H-D-I-C-H-D-I。染色体序列[68534278568123523123574167841764]。

在相同条件下，应用标准遗传算法得出的最佳调度甘特图如图3(b)所示，系统的总加工时间为2 280 s，设备总工作时间为1 310 s，AGV行走序列：H-C-I-D-H-A-I-D-H-C-I-D-H-B-I-G-H-D-I-C-H-D-I-H-C-I-N-H-D-I-H-B-I-D-H-C-I-M-H-D-I-H-A-I-F-H-D-I-A-H-D-I-H-A-I-E-H-D-I-H-B-I-D-H-C-I-Q-H-D-I-C-H-D-I-H-C-I-N-H-D-I-A-H-E-I-D-H-C-I-Q-H-M-I-E-H-D-I-H-B-I-G-H-D-I-H-C-I-M-H-D-I-H-A-I-E-H-G-I-Q-H-N-I-L-H-F-I-Q-H-D-I-H-C-I-D-H-A-I-E-H-D-I-C-H-D-I-H-C-I-D-H-B-I-L-H-D-I-H-A-I-F-H-D-I-B-H-D-I-H-B-I-D-H-C-I-Q-H-D-I-H-C-I-M-H-D-I-C-H-M-I-D-H-C-I-N-H-D-I-C-H-D-I-A-H-F-I-Q-H-D-I-C-H-D-I。染色体序列: [65433884376482552171482712765631]。

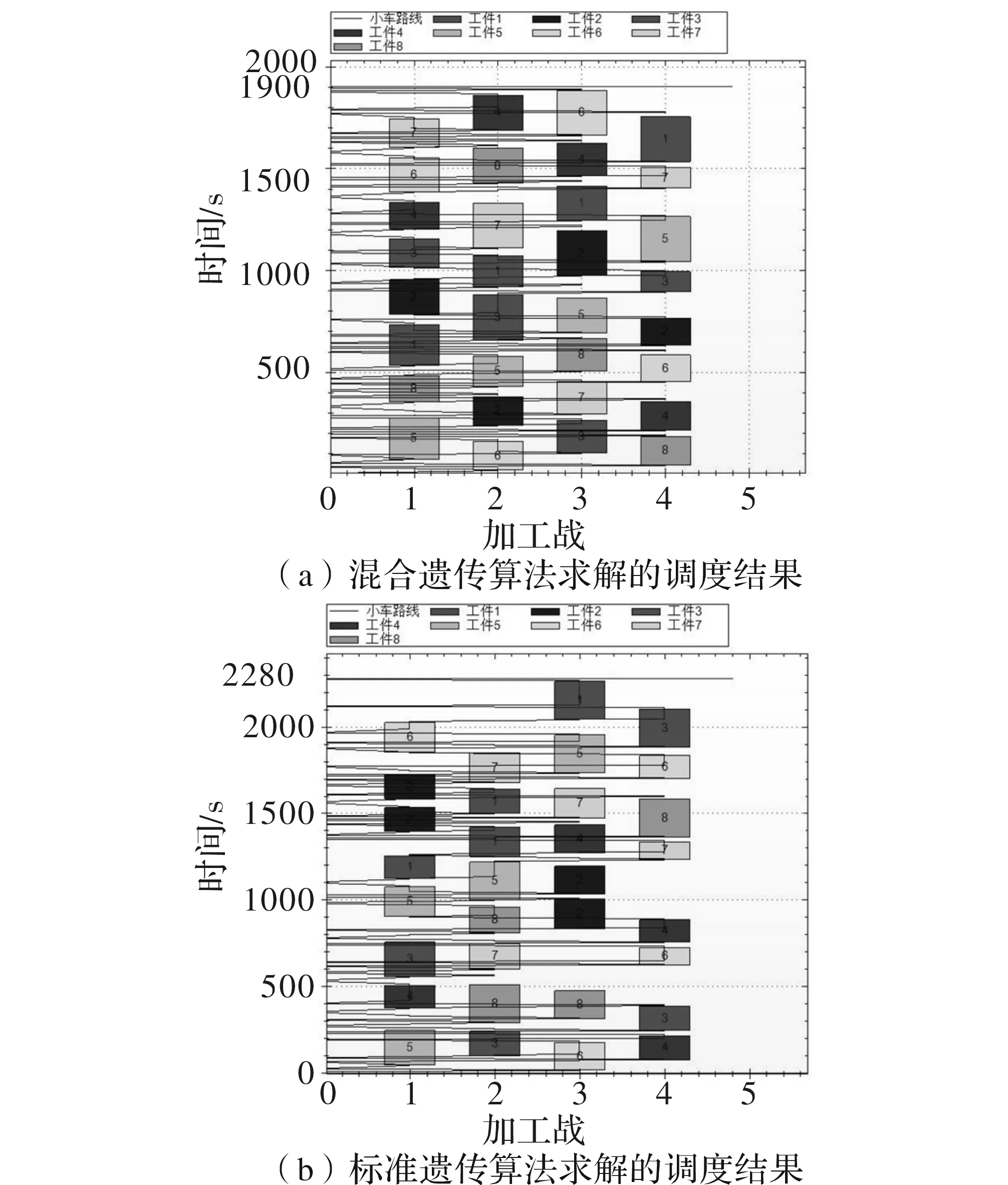
图3　分别应用混合遗传算法和标准遗传算法时8个工件的调度结果对比

在不同工件数目的情况下，分别采用标准遗传算法和改进的混合遗传算法对协同制造系统调度模型进行调度仿真，得到结果如表4所示。在相同的设备平均加工时间条件下，改进的混合遗传算法的设备平均利用率约为68%，而标准遗传算法的设备平均利用率约为57%。可见，较之标准遗传算法，改进的混合遗传算法能较大程度地减少系统的总加工时间、提高设备平均利用率。此外，随着加工工件数目的增多，相对于标准遗传算法，改进的混合遗传算法节省的系统总加工时间也逐步增加，设备的平均利用率也有增加趋势。

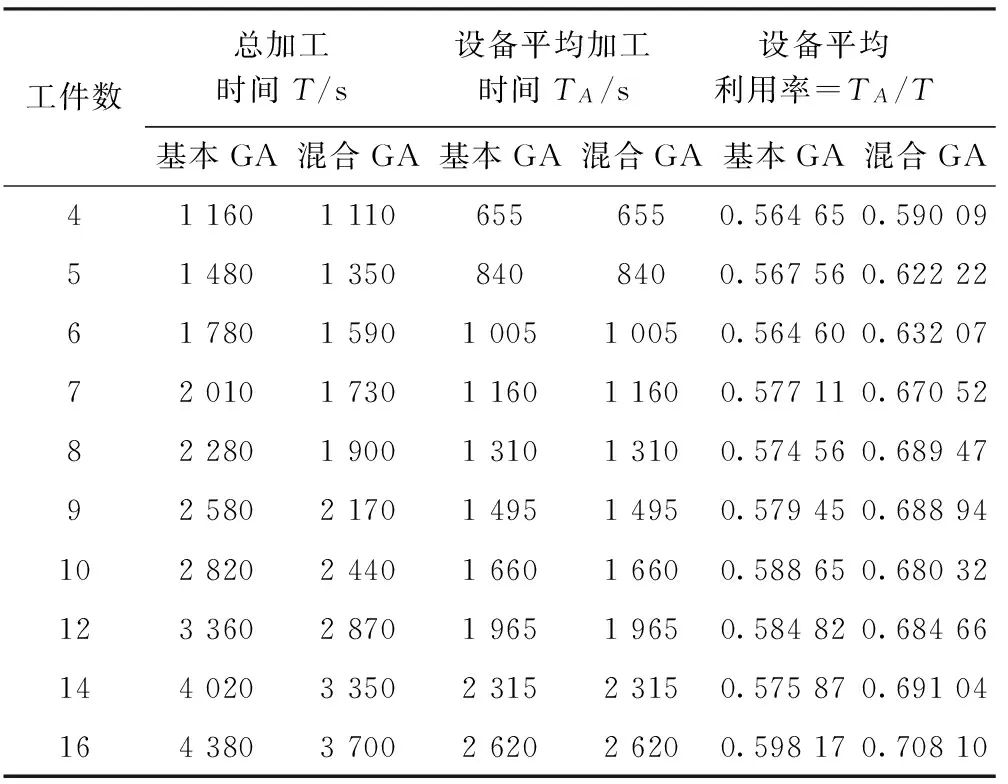
表4　不同工件数情况下两种算法的调度对比结果

5结束语

建立了具有单AGV约束的协同制造系统调度模型，该模型通过改进的混合遗传算法求解实现工件与单AGV的集成调度优化。仿真实验证明该算法是可行的，与标准遗传算法相比，能有效优化AGV运动路径、提高系统调度效率和设备利用率、降低系统总加工时间。为具有AGV约束的柔性生产调度系统提供一种有效的实践途径。针对该模型，还可进一步考虑实际生产中的一些动态因素，例如紧急任务的下达、设备故障以及工序延误等情况，这些突发状况的处理亟待深入研究。

参考文献

[1]周巧.面向缓存有限的柔性制造系统单AGV调度研究[D].广州:广东工业大学,2014.

[2]夏谦,雷勇,叶小勇.遗传算法在AGV全局路径优化中的应用[J].四川大学学报:自然科学版,2008,45(5):1129-1136.

[3]李莉,张立明,詹跃东.求解AGV路径优化问题的遗传算法参数优化[J].昆明理工大学学报,2006,31(4):26-29,38.

[4]杜亚江,郑向东,亢丽君.基于遗传禁忌搜索算法的AGV物料输送调度问题研究[J].物流科技,2013(7):1-4.

[5]李惠光,贾建成,冷春辉.基于分步控制算法的多AGV路径规划[J].控制工程,2010(S2):93-96.

[6]Goldberg D E.Genetic algorithms in search, optimization and machine learning[M]. MA,USA: Addison-Wesley, 1989.

[7]赵卫.模拟退火遗传算法在车间作业调度中的应用[J].计算机仿真,2011,28(7):361-364.

[8]王全.混合遗传算法及其改进[J].安徽建筑工业学院学报:自然科学版,1999,7(4):59-62.

[9]Abdelsalam H M E,Bao Han P.A simulation-based optimization framework for product development cycle time reduction[J].IEEE Transactions on Engineering Management,2006,53(1):69-85.

[10]Holsapple C W,Jacob V S,Pakath R,et al.A genetics-based hybrid scheduler for generating static schedules in flexible manufacturing contexts[J]. IEEE Transactions on Systems, Man and Cybernetics,1993,23(4):953-971.

[11]董义军,张功,张洁.单无人搬运车/单缓冲区约束的柔性生产系统调度研究[J].上海交通大学学报,2010,44(4):528-534.

Research on Scheduling for Collaborative Manufacturing System Based on Hybrid Genetic Algorithm

REN Naifei，YU Lu

(School of Mechanical Engineering, Jiangsu University, Zhenjiang 212013, China)

AbstractBased on the Collaborative Manufacturing System (CMS) consisting of multiple processing stations, a centralized storage area and an Automatic Guided Vehicle (AGV), a mathematical model was built on analysis of the resource constrained problem. The architecture of a dispatching approach with hybrid genetic algorithm was proposed to solve the scheduling problem under resource constraint of the single AGV. This modified hybrid genetic algorithm improved the method of coding, crossover and mutation, which can optimize the job’s machining sequence and the action sequences of AGV movement effectively. Finally, the simulation experiment results in CMS showed that the proposed method is feasible for the integrated scheduling for CMS with the AGV constraint.

Keywordshybrid genetic algorithm; automatic guided vehicle; production scheduling; collaborative manufacturing system; computer simulation

收稿日期:2015-10-25

作者简介:任乃飞(1964-)，男，博士，教授，博士生导师。研究方向：现代集成制造。于璐(1990-)，女，硕士研究生。研究方向：柔性制造系统关键技术。

doi:10.16180/j.cnki.issn1007-7820.2016.06.009

中图分类号TP306.1；TH165

文献标识码A

文章编号1007-7820(2016)06-029-05