基于剪切波的变分图像放大方法

王　鹏，吴玉莲

(1.中航工业西安航空计算技术研究所 13室，陕西 西安 710065；2.西安医学院 卫生管理系，陕西 西安 710021)

基于剪切波的变分图像放大方法

王鹏1，吴玉莲2

(1.中航工业西安航空计算技术研究所 13室，陕西 西安 710065；2.西安医学院 卫生管理系，陕西 西安 710021)

摘要针对图像放大的Chambolle 变分模型会出现阶梯效应的现象， 文中提出了一种基于Shearlet光滑分解空间的变分模型。利用有界变差空间和Shearlet分解空间的关系，特别是Shearlet分解空间的半范与加权Shearlet系数之间的等价关系,将所求的变分问题转化为基于Shearlet域的变分问题,其解归结于简单的Shearlet阈值。实验仿真表明，该方法放大后的图像有效地消除了阶梯块效应，保持了更多的细节，具有更高的峰值信噪比。

关键词图像放大；剪切波; 变分模型；分解空间

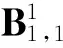
1基础知识

1.1Shearlet变换

剪切波可利用仿射系统理论将几何和多尺度分析结合起来的方法构造。当维数n=2时，具有合成膨胀的仿射系统为

SAB(ψ)={ψj,l,k(x)=|detA|j/2ψ(BlAj-k):

j,l∈Z,k∈Z2}

(1)

其中,ψ∈L2(R2),A和B是2×2可逆矩阵,|detB|=1。若SAB(ψ)具有紧框架,则SAB(ψ)的元素成为合成小波。其中Aj与尺度相关联,Bl与保持面积不变的几何相关联

1.2Chambolle图像放大模型

若讨论的图像是M×N的二维矩阵,X表示空间CM×N,Z是X的一个子空间,g∈Z表示一幅粗糙的低分辨图像。比如,当放大2倍数时,Z表示为

Z={g∈X|g2k,2l=g2k-1,2l=g2k,2l-1=g2k-1,2l-1,

k≤M/2,l≤N/2}

Chambolle[4]的图像放大模型为

(2)

其中，u是放大后的图像；A是在空间Z上的正交投影。显然有Ag=g且

(3)

因此，Chambolle图像放大模型变为

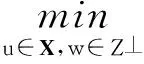
(4)

针对上述最小值问题，Chambolle给出了一种求解的迭代算法,该方法尽管能得到较好的图像放大效果；但由于此方法是基于TV的方法，所以最后处理结果有阶梯块效应，并不能保持更多的细节信息。为克服这些缺点本文提出基于变分Shearlet的图像放大模型。

2基于剪切波的变分图像放大算法

(5)

(6)

(7)

该问题等价于最小化下列泛函

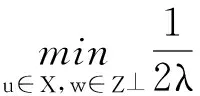
(8)

根据等价关系(6)，有

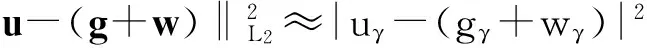
其中，uγ,gγ,wγ分别表示函数的Sheartlet系数，从而得到下列Sheartlet域的等价变分序列

(9)

式中，Λ表示全体的Sheartlet系数指标集。

求解最小化模型(9)相当于求解以下两个耦合问题：

(1)假设wγ固定 , 求泛函求(9)关于uγ的最小解相当于求解

(10)

的解为

uγ=T2-j/4λ(gγ+wγ)

(11)

其中，T1/λ(β)=sign(β)(|β|-1/λ)为软阈值算子;

(2)假设uγ固定 , 求泛函式(11)关于wγ的最小解相当于求解

(12)

的解为wγ=TL(uγ-gγ) ,其中TL表示把函数的Sheartlet系数的低频部分阈值为零。

综上可知泛函(9)最小化问题的解可用以下迭代方法得到，其算法为：

(1) 初始化(wγ)0=0；

(2)迭代 (uγ)n=T2-j/4λ(gγ+(wγ)n-1)，(wγ)n=TL((uγ)n-gγ);

假设ε是一个事先给定的小的正数，若满足条件max(|un+1-un|)≤ε就停止迭代。

3仿真实验

下面给出几种不同方法应用于不含噪声和带有噪声图像的放大比较。先将原图下采样缩小一定的倍数作为实际获取的图像，然后再放大。为比较方便，所有实验图都进行过5层Shearlet分解，第1层为低通，第2～3层为带通，最后一层为高通。经过多次实验可观察到，当λ在各层取统一的常数值时实验效果并不理想。而是当在带通图像层参数λ=kj,j=2,3,4,k=0.4,高通图像层参数λ=60, 低通图像层参数λ=0时，效果较好。λ当图像不含噪声时，文中新算法与Chambolle[2]放大模型和冯[3]小波放大以及仿真软件Matlab自带的双线性插值进行比较，图1是4种算法对Camera(128×128)图像进行放大两倍的结果。可看出Chambolle放大模型得到的图像边缘锯齿现象比较严重，而新模型不仅保持了边缘的锐度，且边缘轮廓清晰、光滑，同时放大视觉效果比双线性插值略好。当对含噪图像(高斯噪声方差为15)进行放大时，实验结果如图2所示。图2对Lena(128×128)噪声图像放大两倍的结果，Chambolle放大模型有明显阶梯块效应，图像的特征细节丢失较多，新方法得到的图像细节丰富，如图像中帽子上的皱褶及头发比较清晰。

下面对6幅图像进行实验，用峰值信噪比(PSNR)和均方误差(RMSE)来评价图像放大效果的优劣。实验数据如表1所示，由这两个指标来看，本文方法明显优于其他两种模型，尤其当放大倍数为2时，新方法比Chambolle模型的PSNR高1dB以上，且比冯象初[3]的中小波方法高0.5dB以上；因此得到质量更好的放大图像。

图1　Lena噪声图像放大两倍的结果比较

图2　Camera图像放大两倍的结果比较

图像噪声方差放大倍数Chambolle模型PSNRRMSE文献[3]算法PSNRRMSE本文算法PSNRRMSECamera128×128σ=0222.43619.26323.29917.44223.93316.214Lena256×256σ=0229.5968.44729.7188.32931.3766.882Lena128×128σ=0424.61514.75325.44213.61725.78313.103Plane128×128σ=0225.52313.50326.84411.59627.55510.685Lena128×128σ=15224.36415.49224.54215.11625.25113.929Peppers128×128σ=15222.74318.59522.79318.49223.86316.345

4结束语

与传统插值放大图像不同，本文从变分的角度提出一种新的图像放大算法。该算法用Shearlet空间半范刻画图像的正则性构造了一个变分泛函，然后通过最小化变分泛函得到放大图像。根据Shearlet空间半范与Shearlet加权系数之间的等价关系，可将该泛函的最小化问题转化到Shearlet域中用迭代(迭代次数最多2次)的方法求解。新方法的视觉效果比其他两种方法更好,有明显的优越性。

参考文献

[1]ZhuNing,WuJing，WangZhongqian.Imagezoomingbasedonpartialdifferentialequations[J].JournalofComputer-AidedDesignandComputerGraphics,2005,17(9):1941-1945.

[2]ChambolleA.Analgorithmfortotalvariationminimizationandapplications[J].JournalofMathematicalImagingandVision,2004(20):89-97.

[3]冯象初,姜东焕,徐光宝.基于变分和小波变换的图像放大算法[J].计算机学报,2008,31(2):340-345.

[4]Cand`esEJ,DemanetL,DonohoDL,etal.Fastdiscretecurvelettransforms[J].SIAMMultiscaleModelSimulation,2006,5(3):861-899.

[5]DoMN,VetterliM.Thecontourlettransform:anefficientdirectionalmultiresolutionimagerepresentation[J].IEEETransactionsonImageProcessing,2005,14(12):2091-2106.

[6]GuoK,LabateD.OptimallysparsemultidimensionalrepresentationusingShearlets[J].SIAMJournalonMathematicalAnalysis,2007,39(1):298-318.

[7]石程.基于Shearlet的图像融合方法研究[D].西安:西安电子科技大学,2012.

[8]刘成皓,刘文波,张弓.基于Shearlet变换的SAR图像自适应去噪算法[J].电子科技, 2012,25(6):83-86.

[9]LabateD,MantovaniL,NegiPS.Shearletsmoothnessspaces[J].JournalofFourierAnalysis&Applications, 2013, 19(3):577-611.

[10]EasleyG,LabateD,LimW.Sparsedirectionalimagerepresentationsusingthediscreteshearlettransform[J].Applied&ComputationalHarmonicAnalysis, 2008, 25(1):25-46.

Combining Variation and Shearlet Transform for Image Zooming

WANG Peng1，WU Yulian2

(1.No.13 Room, AVIC Xi'an Aeronautical Engineering Institute of Computing Technology, Xi'an 710065, China;2. Department of Health ,Xi’an Medical College, Xi’an 710021，China)

AbstractAs the Chambolle variational model of image magnification results in the staircase effect. a new algorithm for image zooming based on shearlet smoothness decomposition spaces is proposed. The new algorithm translates the variational problem that is solved into a sequence based shearlet field through the equivalent relationship between semi-norm of shearlet-type decomposition spaces and the weighted shearlet coefficients, solution of the proposed model approximately equals to different shearlet shrinkages. Experimental results have verified that the new algorithm can effectively eliminate the staircase effect of zoomed images and keep more details with a higher peak signal to noise ratio.

Keywordsimage zooming; Shearlet; variational model; decomposition spaces

收稿日期:2015-11-07

基金项目:陕西省教育厅基金资助项目(15JK1371)；西安医学院博士科研启动基金资助项目(2015DOC25)

作者简介:王鹏(1978-)，男，工程师。研究方向：图像处理。

doi:10.16180/j.cnki.issn1007-7820.2016.06.042

中图分类号TP391.41

文献标识码A

文章编号1007-7820(2016)06-146-04