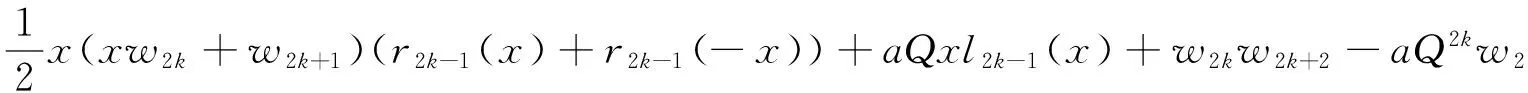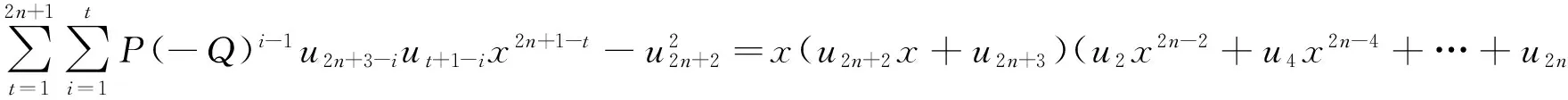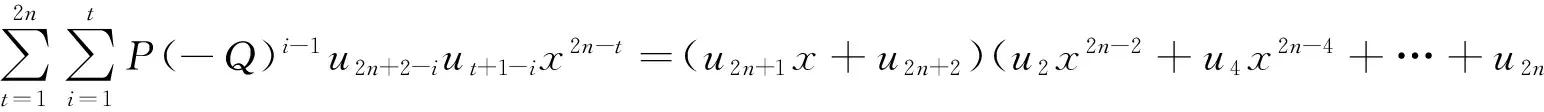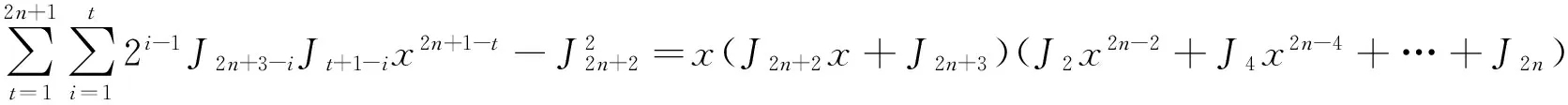涉及二阶线性递归序列的两类多项式的因式分解
2016-06-30孙苹,胡宏
孙 苹, 胡 宏
(1.宁夏大学 数学与计算机学院, 宁夏 银川 750021; 2.淮阴师范学院 数学科学学院, 江苏 淮安 223300)
涉及二阶线性递归序列的两类多项式的因式分解
孙苹1,2, 胡宏2
(1.宁夏大学 数学与计算机学院, 宁夏 银川750021; 2.淮阴师范学院 数学科学学院, 江苏 淮安223300)
摘要:定义了与二阶线性递归序列{wn}相关的序列{di,j}和{},及与序列{wn},{di,j}和{}相关的多项式 rn(x),ln(x),tn(x) 和,根据{wn}的递推关系和相关性质,研究了{di,j}和{}的相关性质,得到了一系列关于ln(x),tn(x)和的多项式的因式分解.
关键词:二阶线性递归序列; 多项式; 因式分解
0引言
二阶线性递归序列{wn(a,b;P,Q)}是指满足如下递推关系的序列:
wn+1=Pwn-Qwn-1,w0=a,w1=b,n=1,2,3,…
(1)
一般地,记wn(a,b;P,Q)=wn,当a=0,b=1时,记wn(0,1;P,Q)=un(P,Q),简记为un.当a=2,b=P时,记wn(2,P;P,Q)=vn(P,Q),简记为vn.当a=0,b=1,P=1,Q=-1时,记wn(0,1;1,-1)=Fn,Fn就是著名的Fibonacci数.当a=2,b=1,P=1,Q=-1时,记wn(2,1;1,-1)=Ln,Ln就是著名的Lucas数[1].当a=0,b=1,P=1,Q=-2时,记wn(0,1;1,-2)=Jn,Jn就是Jacobsthal数.当a=2,b=1,P=1,Q=-2时,记wn(2,1;1,-2)=jn,jn是Jacobsthal-Lucas数[2].当a=0,b=1,P=2,Q=-1时,记wn(0,1;2,-1)=Pn,Pn就是Pell数.当a=2,b=2,P=2,Q=-1时,wn(2,2;2,-1)=Qn,Qn是Pell-Lucas数[3].
文[4]中,令
(2)
(3)
vn(x)=m(n,1)xn+m(n,2)xn-1+…+m(n,n+1)
(4)
(5)
得到了多项式vn(x)和wn(x)的因式分解:
v2k+1(x)=(xF2k+1+F2k+2)(F2x2k+F4x2k-2+…+F2kx2+F2k+2)
(6)
v2k(x)-F2kF2k+2=x(xF2k+F2k+1)(F2x2k-2+F4x2k-4+…+F2k)
(7)
(8)
w2k(x)=(xF2k+1+F2k+2)(F2x2k-2+F4x2k-4+…+F2k)
(9)

(10)
(11)
rn(x)=w1xn+w2xn-1+…+wn+1,n=1,2,…
(12)
ln(x)=wn+1xn-Qwnxn-1+…+(-Q)nw1,n=1,2,…
(13)
tn(x)=dn,1xn+dn,2xn-1+…+dn,n+1,n=1,2,…
(14)
(15)
特别地, 当i,h为正整数且h≥2时,易得
di,i+h=Pdi,i+h-1-Qdi,i+h-2
(16)
(17)

1相关引理
由式(1)和(10)可得
引理1设n为任意的正整数,则
dn,n=wnwn+1-(-Q)nab
(18)
引理2设n为任意的正整数,则
(19)
引理3设i,j为任意的正整数,i≤j时,有
(20)
证由式(18)和(19)知j=i或i+1时,式(20)成立.
假设当i≤j 由归纳法知式(20)成立.由式(10)和(11) 可得 引理4设i,j为任意的正整数,则 (21) 2主要结果 定理1设k为任意正整数,则 (22) (23) 证令n维列向量Xn-1=(xn-1,xn-2,…,x,1)T, 当k≥1时有 t2k+1(x)=(d2k+1,1,d2k+1,2,…,d2k+1,2k+1,d2k+1,2k+2)X2k+1, 由式(10)和(20)可得 t2k+1(x)=(d1,2k+1,d2,2k+1,…,d2k+1,2k+1,d2k+1,2k+2)X2k+1= (w2w2k+1+aQw2k+1,w2w2k+2-aQ2w2k,w4w2k+1+aQ3w2k-1,…, w2k+2w2k+1+aQ2k+1w1,w2k+2w2k+2+aQ2k+1w2)X2k+1= w2x2k(xw2k+1+w2k+2)+w4x2k-2(xw2k+1+w2k+2)+…+ w2k+2(xw2k+1+w2k+2)+aQx(w2k+1x2k-Qw2kx2k-1+…+Q2kw1)+aQ2k+1w2= 类似地 t2k(x)=(d2k,1,d2k,2,…,d2k,2k,d2k,2k+1)X2k, 由式(10)和(20)可得 t2k(x)=(d1,2k,d2,2k,…,d2k,2k,d2k,2k+1)X2k= (w2w2k+aQw2k,w2w2k+1-aQ2w2k-1,w4w2k+aQ3w2k-2,…, w2kw2k+aQ2k-1w2,w2kw2k+1-aQ2kw1,w2kw2k+2-aQ2kw2)X2k= w2x2k-1(xw2k+w2k+1)+w4x2k-3(xw2k+w2k+1)+…+w2kx(xw2k+w2k+1) +w2kw2k+2-aQ2kw2+aQx(w2kx2k-1-Qw2k-1x2k-2+…-Q2k-1w1)= 综上,定理1得证. 注1文[4]中定理4.1就是在定理1中取a=0,b=1,P=1,Q=-1时的特殊情况. 定理2设k为任意正整数,则 (24) (25) 证令n维列向量 由式(10),(20)和(21)可得 (w2w2k+2+aQw2k+2,w2w2k+3-aQ2w2k+1,w4w2k+2+aQ3w2k,…, w2x2k(xw2k+2+w2k+3)+w4x2k-2(xw2k+2+w2k+3)+…+ aQ(w2k+2x2k+1-Qw2k+1x2k+…-Q2k-1w3x2+Q2kw2x-Q2k+1w1)+abQ2k+2= 类似地 由式(10),(20)和(21)可得 w2x2k-1(xw2k+1+w2k+2)+w4x2k-3(xw2k+1+w2k+2)+…+ w2kx(xw2k+1+w2k+2)+aQ(w2k+1x2k-Qw2kx2k-1+…-Q2k-1w2x)= aQ(w2k+1x2k-Qw2kx2k-1+…-Q2k-1w2x+Q2kw1)-abQ2k+1= 综上定理2得证. 注2文[4]中定理4.2就是在定理2中取a=0,b=1,P=1,Q=-1时的特殊情况. 3相关推论 在式(22)~(25)中,当a=0,b=1时,可得 推论1设n为正整数时,有 (u2n+1x+u2n+2)(u2x2n+u4x2n-2+…+u2nx2+u2n+2). x(u2nx+u2n+1)(u2x2n-2+u4x2n-4+…+u2n-2x2+u2n). 推论2设n为正整数时,有 在式(22)~(25)中,当a=2,b=P时,可得 推论3设n为正整数时,有 (v2n+1x+v2n+2)(v2x2n+v4x2n-2+…+v2nx2+v2n+2). 2Q2nv2-v2nv2n+2=x(v2nx+v2n+1)(v2x2n-2+v4x2n-4+…+v2n-2x2+v2n). 推论4设n为正整数时,有 x2(v2n+2x+v2n+3)(v2x2n-2+v4x2n-4+…+v2n-2x2+v2n). x(v2n+1x+v2n+2)(v2x2n-2+v4x2n-4+…+v2n-2x2+v2n). 在式(22)~(25)中,当a=0,b=1,P=1,Q=-2时,可得 推论5设n为正整数时,有 (J2n+1x+J2n+2)(J2x2n+J4x2n-2+…+J2nx2+J2n+2). x(J2nx+J2n+1)(J2x2n-2+J4x2n-4+…+J2n-2x2+J2n). 推论6设n为正整数时,有 在式(22)~(25)中,当a=0,b=1,P=2,Q=-1时,可得 推论7设n为正整数时,有 (P2n+1x+P2n+2)(P2x2n+P4x2n-2+…+P2nx2+P2n+2). x(P2nx+P2n+1)(P2x2n-2+P4x2n-4+…+P2n-2x2+P2n). 推论8设n为正整数时,有 在式(22)~(25)中,当a=2,b=1,P=1,Q=-1时,可得 推论9设n为正整数时,有 (L2n+1x+L2n+2)(L2x2n+L4x2n-2+…+L2nx2+L2n+2). x(L2nx+L2n+1)(L2x2n-2+L4x2n-4+…+L2n-2x2+L2n). 推论10设n为正整数时,有 x2(L2n+2x+L2n+3)(L2x2n-2+L4x2n-4+…+L2n-2x2+L2n). x(L2n+1x+L2n+2)(L2x2n-2+L4x2n-4+…+L2n-2x2+L2n). 在式(22)~(25)中,当a=2,b=1,P=1,Q=-2时,可得 推论11设n为正整数时,有 (j2n+1x+j2n+2)(j2x2n+j4x2n-2+…+j2nx2+j2n+2). x(j2nx+j2n+1)(j2x2n-2+j4x2n-4+…+j2n-2x2+j2n). 推论12设n为正整数时,有 x2(j2n+2x+j2n+3)(j2x2n-2+j4x2n-4+…+j2n-2x2+j2n). x(j2n+1x+j2n+2)(j2x2n-2+j4x2n-4+…+j2n-2x2+j2n). 在式(22)~(25)中,当a=2,b=2,P=2,Q=-1时,可得 推论13设n为正整数时,有 (Q2n+1x+Q2n+2)(Q2x2n+Q4x2n-2+…+Q2nx2+Q2n+2). x(Q2nx+Q2n+1)(Q2x2n-2+Q4x2n-4+…+Q2n-2x2+Q2n). 推论14设n为正整数时,有 x2(Q2n+2x+Q2n+3)(Q2x2n-2+Q4x2n-4+…+Q2n-2x2+Q2n) x(Q2n+1x+Q2n+2)(Q2x2n-2+Q4x2n-4+…+Q2n-2x2+Q2n). 参考文献: [1]Zhao F Z,Wang T M.Some identities involving the Fibonacci and Lucas numbers[J].Ars Combinatoria,2004(72):311-318. [2]张慧婷,王军霞.有关Bell多项式与Jacobsthal数的恒等式[J].甘肃科学院学报,2010,22(1):39-42. [3]贾彦益,杨胜良.Pell-Lucas矩阵及其应用[J].甘肃科学院学报,2010,22(4):13-17. [4]Clare Kimberling.Fusion,Fission and Factors[J].The Fibonacci Quarterly,2014,52(3):195-202. [责任编辑:李春红] The Decomposition of two Kinds of Polynomials Involving 2-order Linear Recursive Sequence SUN Ping1,2, HU Hong2 (1.School of Mathematics and Computer Science, Ningxia University, Yinchuan Ningxia 75000, China)(2.School of Mathematical Science, Huaiyin Normal University, Huaian Jiangsu 223300, China) Abstract:In this paper,new sequences{di,j}and{i,j},and their related 2-order linear recursive sequence{wn}were defined,and some polynomials rn(x),ln(x),tn(x)andn(x)associated with {wn},{di,j}and{i,j}were defined.According to the recurrence relation and related properties of sequence{wn} and we studied the properties of{di,j}and{i,j},a series of ln(x),tn(x) andn(x) polynomial factorization were obtained. Key words:2-order linear recursive sequences; polynomial; decomposition 收稿日期:2016-02-12 通讯作者:胡宏(1967-), 女, 江苏金湖人, 教授, 研究方向为数论与组合数学. E-mail: hysyhh@163.com 中图分类号:O157 文献标识码:A 文章编号:1671-6876(2016)02-0104-06