基于对数灰关联度的IGOWLA算子最优组合预测模型

吴　齐, 杨桂元, 储　震

(安徽财经大学 数量经济研究所, 安徽 蚌埠　233030)

基于对数灰关联度的IGOWLA算子最优组合预测模型

吴齐, 杨桂元, 储震

(安徽财经大学 数量经济研究所, 安徽 蚌埠233030)

摘要:在对数灰关联度和诱导广义有序加权对数平均算子(IGOWLA)等概念的基础上,构建了基于对数灰关联度的IGOWLA算子的最优组合预测模型,并引入组合预测模型的优性及非劣性定义．实例计算结果表明,提出的方法确为一种优性组合预测,能够有效地提高预测精度．

关键词:对数灰色关联度; IGOWLA算子; 优性组合预测

0引言

自1969年Bates和Granger[1]提出组合预测模型以来,组合预测方法被广泛应用于各个领域的预测分析．单项预测方法往往从某个角度对事物现象进行预测,不可避免地造成预测结果的片面性,因此,组合预测思想的提出引发国内外学者对该理论的拓展研究和应用研究．

1988年,Yager[2]学者提出有序加权平均算子(OWA)之后,OWA[3]算子及其拓展后的集成信息算子和应用受到很多学者关注．通过增加诱导值,建立基于诱导有序加权平均算子[4](IOWA)的组合预测模型,该模型的特点是:组合预测的赋权系数与单项预测方法无关,而是与单项预测方法在各时刻上预测精度的大小密切相关．广义有序加权平均算子[5](GOWA)将OWA算子推广到λ次幂的形式．GOWA算子中单项预测数值取对数得到广义有序加权对数平均算子[6](GOWLA)．引入诱导值到GOWA算子中,将GOWA算子推广为诱导广义有序加权平均算子[7](IGOWA),该算子为变权系数算子．若先把单项预测数值取对数后再进行IGOWA算子运算,则该算子推广为诱导广义有序加权对数平均算子[8](IGOWLA)．陈华友等[9]将灰色关联度与算子结合,建立基于灰关联度的组合预测模型,通过给出新的优性组合预测、非劣性组合预测、冗余度等概念,探讨其性质,从而在理论上证明了基于灰色关联度的组合预测模型的有效性．之后,程玲华等[10]、袁宏俊等[11],周礼刚等[12]分别将灰色关联度与加权几何平均算子、IOWA算子、IOWGA算子相结合建立组合预测模型并运用实例说明新建立的组合预测模型的有效性和合理性．

本文试图将灰色关联度和IGOWLA算子相结合,以预测精度作为诱导变量进行有序加权平均集成,通过预测值对数的λ次幂序列与实际值对数的λ次幂序列之间的灰色关联度作为目标函数,提出一种基于灰色关联度的IGOWLA算子最优组合预测模型,并通过实例分析说明该模型的有效性．

1几个基本概念

令

(1)

式(1)中,对(a1,a2,…,an)按从大到小的顺序进行排列,并令bi为其第i大的数值,称OWAW为n维有序加权平均算子,简称OWA算子．

令

(2)

式(2)中,对v1,v2,…,vn按从大到小的顺序进行排列,并令v-index(i)为其第i大的数所对应的a的下标,其中v1,v2,…,vn为诱导变量,称IOWAW为n维诱导有序加权平均算子,简称IOWA算子．定义2表明,IOWA算子中的权系数wi与ai的大小和位置无关,而与诱导值vi所在的位置有关,也就是说a1,a2,…,an是按照诱导值v1,v2,…,vn从大到小的排序结果所进行的一种有序加权算术平均．

(3)

式(3)中,对(a1,a2,…,an)按从大到小的顺序进行排列,并令bi为其第i大的数值,λ∈(-∞,0)∪(0,+∞),称GOWLAW为n维广义有序加权对数平均算子,简称GOWLA算子．

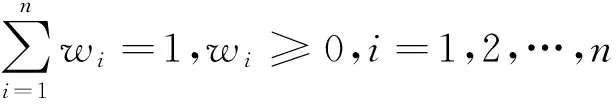
(4)

式(4)中,对v1,v2,…,vn按从大到小的顺序进行排列,并令v-index(i)为其第i大的数所对应的a的下标,其中v1,v2,…,vn为诱导变量,λ∈(-∞,0)∪(0,+∞)．称IGOWLAW为n维广义诱导有序加权对数平均算子,简称IGOWLA算子．

2基于对数灰关联度的IGOWLA算子最优组合模型

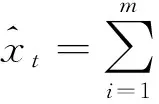
定义5设vit为第i种预测方法在t时刻的预测精度,令

(5)

式(5)中,显然vit∈[0,1]．若将预测精度vit看成预测值xit的诱导值,则各单项预测方法在第t时刻的预测精度vit与其对应在样本区间的预测值xit便构成了一个二维数组序列(〈v1t,x1t〉,〈v2t,x2t〉,…,〈vmt,xmt〉)．由IGOWLA算子定义得到如下定义：

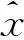
(6)

式(6)中,对v1t,v2t,…,vmt按从大到小的顺序进行排列,并令v-index(it)为其第i大的数所对应的x的下标,其中,t=1,2,…,N．也就是说,基于IGOWLA算子的组合预测系数是根据各单项预测方法在不同时刻上预测精度的相对高低排序结果来进行赋权的．由式(6)可得

(7)

令

ev-index(it)=(lnxt)λ-(lnxv-index(it))λ

(8)

由式(6)～(8)可以得到组合预测在t时刻的对数的λ次幂的预测误差如下

(9)

定义7称γi为第i种单项预测方法预测值对数λ次幂序列与实际观测值对数λ次幂序列的灰色关联度,简称第i种单项预测方法的对数灰关联度;称γ为基于IGOWLA算子组合预测值的对数λ次幂序列与实际观测值对数λ次幂序列的灰色关联度,简称组合预测方法的对数灰关联度．

(10)

(11)

式(10)和(11)中,ρ为分辨系数,ρ∈(0,1),通常取ρ=0.5．不难看出,组合预测方法的对数灰关联度是关于各单项预测方法的权重向量W=(w1,w2,…,wm)T的一个函数,故可记为γ(W)．由灰色关联度原理可知,组合预测方法的有效性与其对数灰关联度呈正比,因此基于对数灰关联度的IGOWLA算子组合预测模型可由式(12)表示:

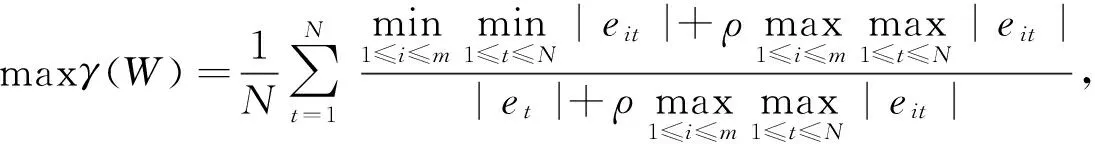
(12)

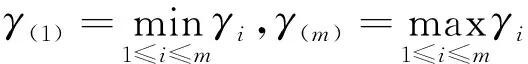
3实例分析

本文选用文[8]的数据对基于灰色关联度的IGOWLA算子组合预测模型的有效性加以实例分析,数据见表1．

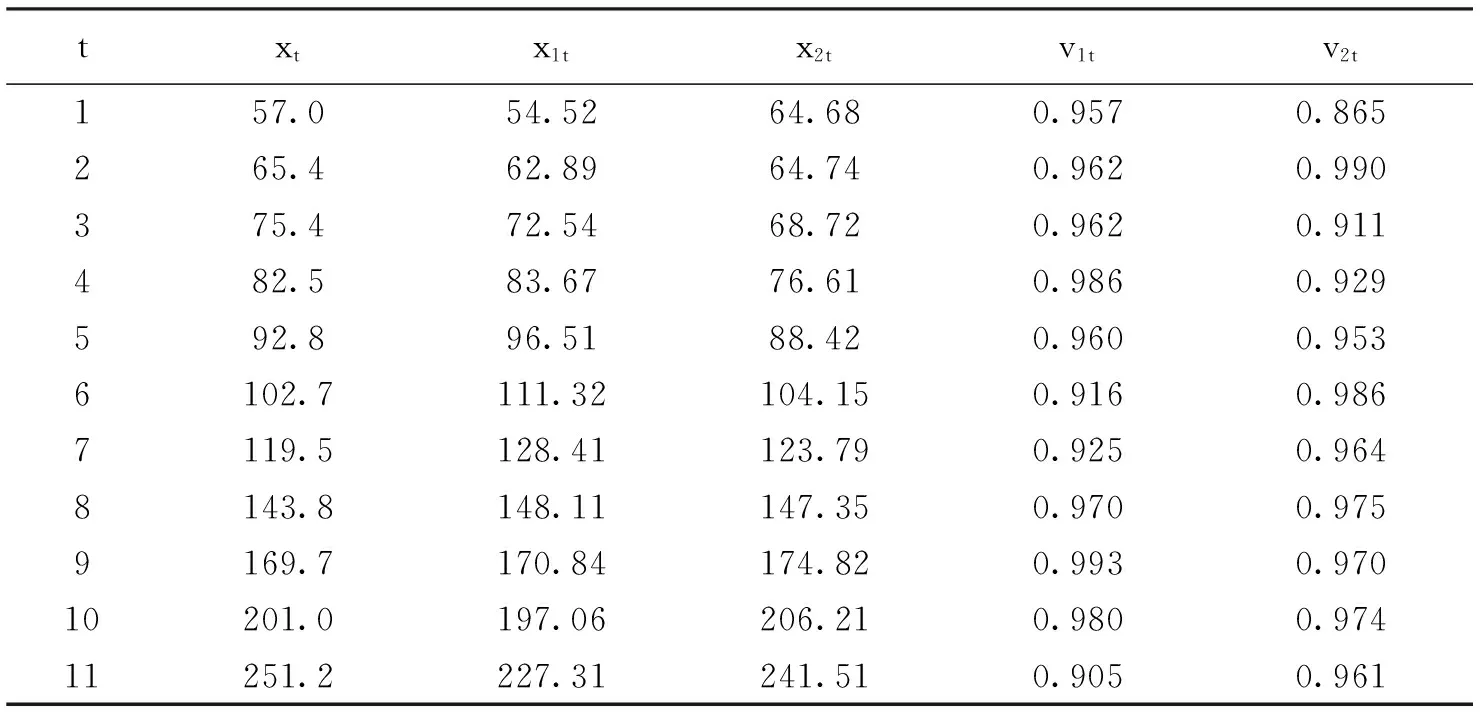
表1　指标实际观测值、单项预测值及其预测精度

表1中,xt为原始序列,x1t和x2t分别为两个单项预测序列,v1t和v2t分别为相应单项预测的预测精度,也为诱导变量．根据表1和式(6),可得到t时刻IGOWLA算子的组合预测值:

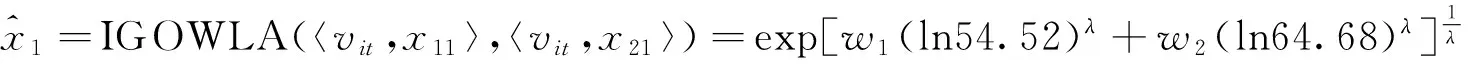
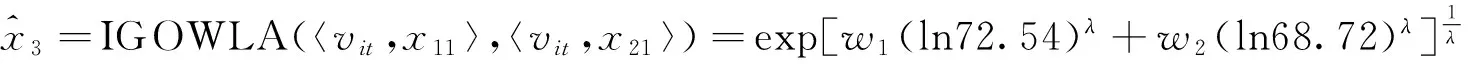
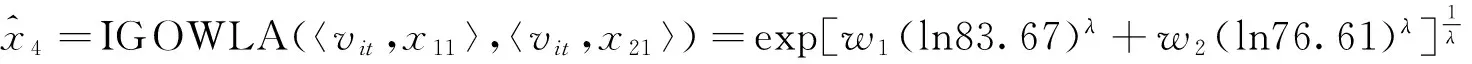
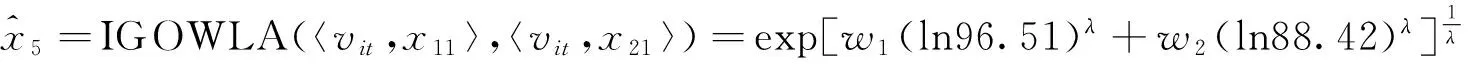
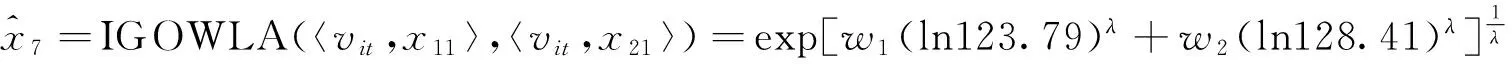
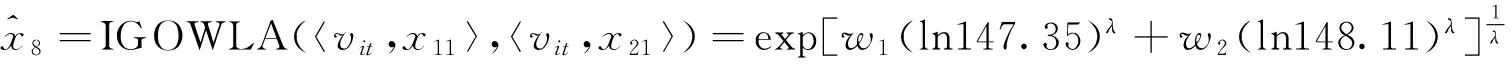
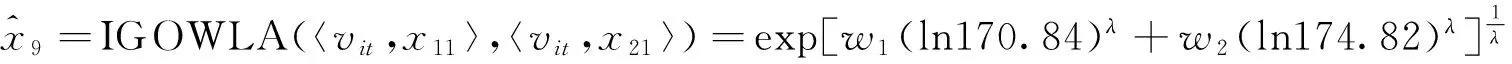
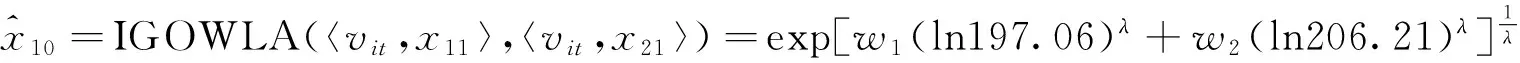
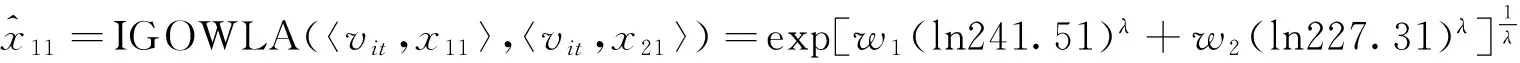
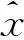
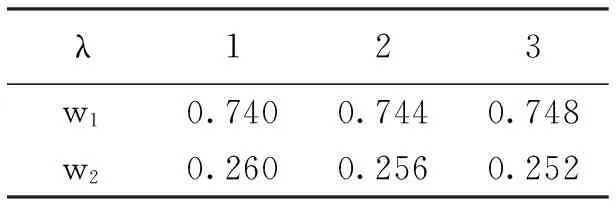
表2　组合预测的最优权系数

关联度的IGOWLA算子组合预测值模型,对式(12)中λ取不同的值进行验证,运用MATLABR2014a软件计算得到最优权系数(表2)．

根据表2,可以到不同参数λ的组合预测值(表3)．选择如下几个误差指标作为基于对数灰关联度的IGOWLA算子组合预测模型的评价指标体系:

具体评价指标值见表4．

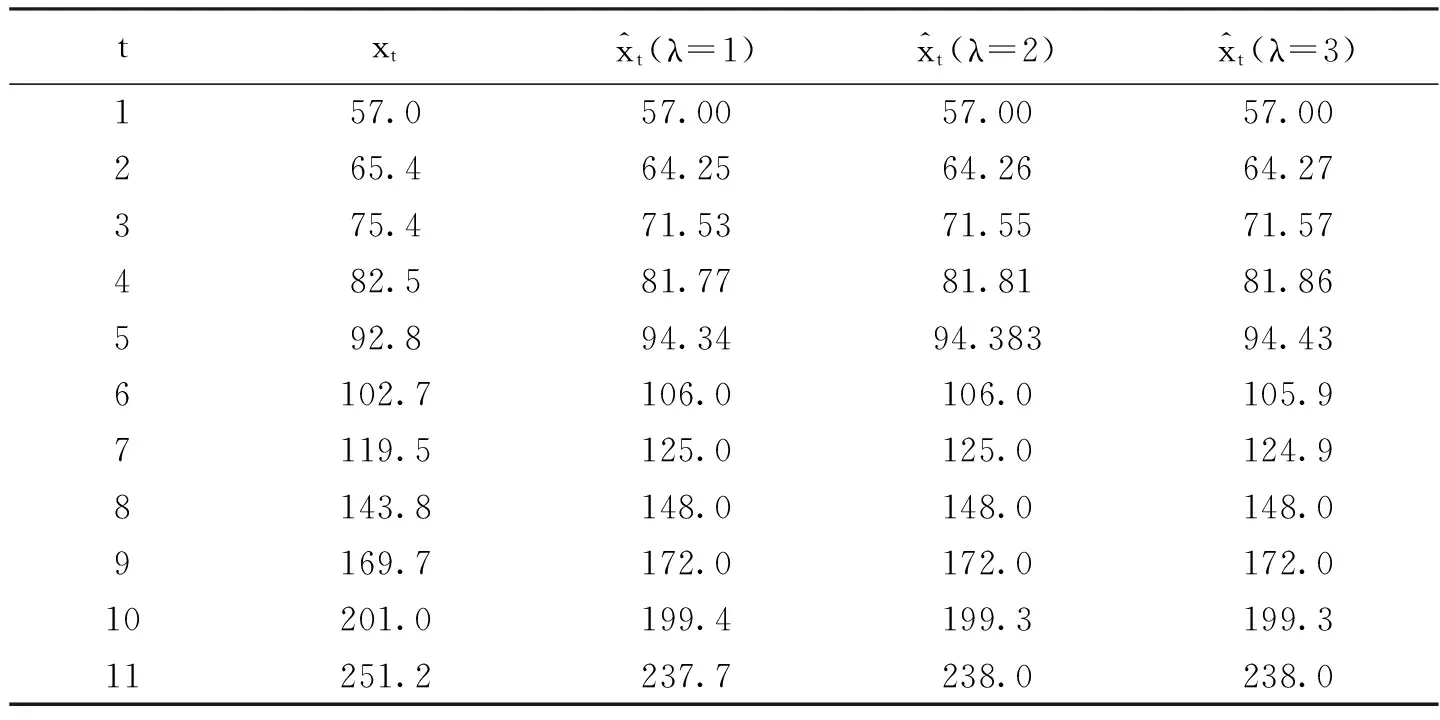
表3　实际值和不同参数的组合预测值

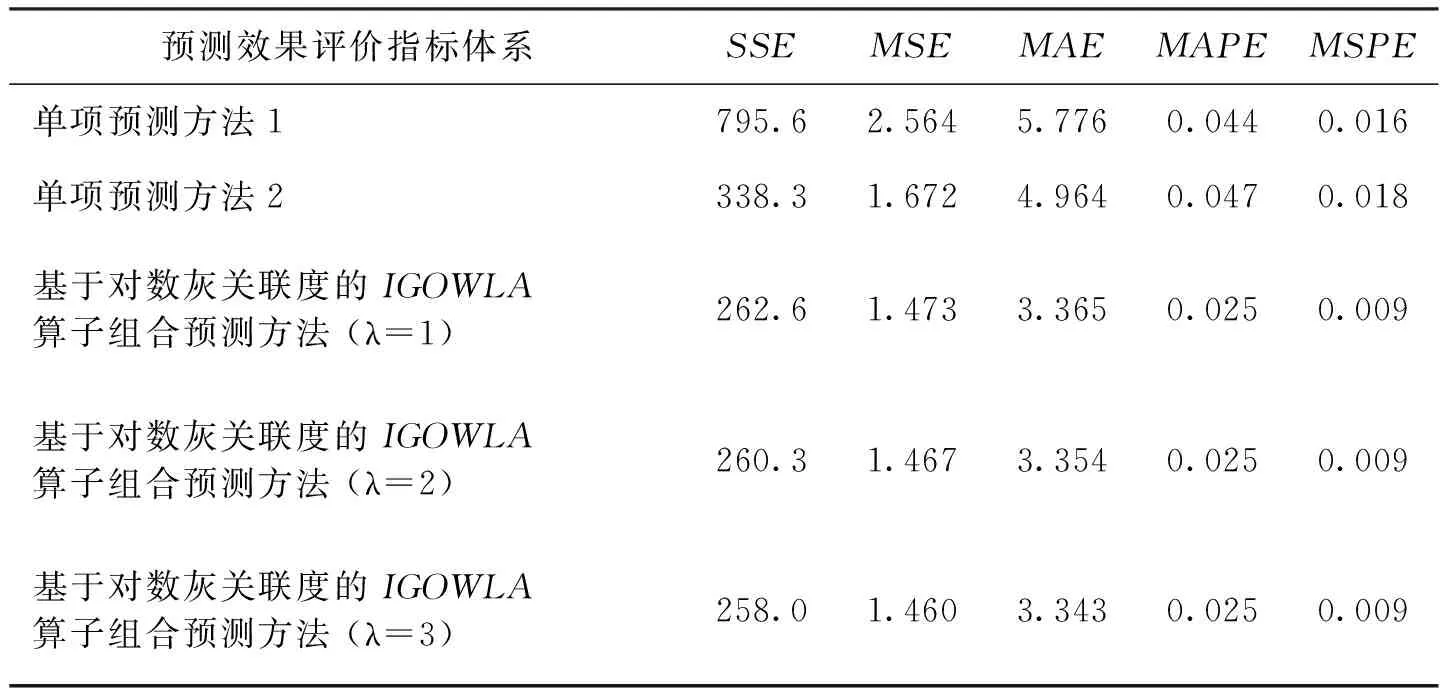
表4　单项预测和组合预测效果评价指标体系表

由表4,相比其他两种单项预测,基于对数灰关联度的IGOWLA算子组合预测模型的各项误差指标值要小得很多．此外还可计算他们的对数灰关联度:当λ=1时,γ1=0.005,γ2=0.005,γ=0.826,此时γ=0.826>max(γ1,γ2)=0.005;当λ=2时,γ1=0.005,γ2=0.005,γ=0.823,此时γ=0.823>max(γ1,γ2)=0.005;当λ=3时,γ1=0.006,γ2=0.005,γ=0.844,γ=0.843>max(γ1,γ2)=0.006．由定义8可知,基于对数灰关联度的IGOWLA算子组合预测模型结果可视为优性组合预测,能够显著提高预测的精度．

4结束语

本文在回顾n维诱导广义有序加权对数平均算子(IGOWLA)基础之上,结合灰色关联度,提出基于对数灰关联度的IGOWLA算子的最优组合预测模型,并借助实例计算表明该组合预测方法的可行性．此外,关于该组合预测模型的一些理论性问题,诸如组合预测的优性、非劣性的存在性以及冗余预测方法的判定等问题,还有待于进一步探讨．

参考文献：

[1]Bates J M,Granger C W J.Combination of forecasts[J].Operation Research Quarterly,1969,20(4):451-468.

[2]Yager R R.On ordered weighted averaging aggregation operators in multicriteria decision making[J].IEEE Transactions on Systems,Man and Cybernetics,1988, 18(1):183-190.

[3]Filev D,Yager R R.On the issue of obtaining OWA operator weights[J].Fuzzy Sets and Systems,1998,94(2):157-169.

[4]陈华友,刘春林.基于IOWA 算子组合预测方法[J].预测,2003,22(6):61-65.

[5]Yager R R.Generalized OWA aggregation operators[J].Fuzzy Optimization and Decision Making,2004,3(1):93-107.

[6]Zhou L G,Chen H Y.Generalized Ordered Weighted Logarithm Aggregation Operators and Their Applications to Group Decision Making[J].International Journal of Intelligent Systems,2010,25(7):683-707.

[7]Merigo J M, Gil-Lafuente A M.The Induced Generalized OWA operator[J].Information Sciences,2009,179(6):729-741.

[8]江立辉,陈华友,丁芳清,等.基于IGOWLA 算子的最优组合预测模型及其应用[J].统计与决策,2015(4):82-85.

[9]陈华友,赵佳宝,刘春林.基于灰色关联度的组合预测模型的性质[J].东南大学学报:自然科学版,2004,31(1):130-134.

[10]程玲华,程华友.基于对数灰关联的加权几何平均组合预测模型的有效性[J].运筹与管理,2007,16(6):69-73.

[11]袁宏俊,陈华友.基于改进灰色关联度的 IOWA 算子最优组合预测模型[J].数学实践与认识,2010,40(11):145-151.

[12]周礼刚,陈华友,韩冰,等.基于对数灰关联度的 IOWGA 算子最优组合预测模型[J].运筹与管理,2010,19(6):33-38.

[责任编辑：李春红]

The Combination Forecasting Model Based on Degree of Logarithm Grey Incidence and Induced Geometric Ordered Weighted Logarithm Averaging(IGOWLA) Operator

WU Qi, YANG Gui-yuang, CHU Zheng

(Institute of Quantitative & Economic Research, Anhui University of Finance and Economic, Bengbu Anhui 233030, China)

Abstract:In this paper, a new combination forecasting model was proposed based on degree of logarithm grey incidence and induced geometric ordered weighted logarithm averaging (IGOWLA) operator by combining the induced ordered geometric ordered weighted logarithm averaging operator and the degree of grey incidence.At the same time, the conception of superior combination forecasting and noninferior combination forecasting was given.Finally, an example is illustrated by using the model.The example showed that the combination forecasting model was effective and reasonable,and it was superior combination forecasting.

Key words:degree of logarithm grey incidence; IGOWLA operator; superior combination forecasting

收稿日期:2016-03-01

基金项目:国家社科基金资助项目“组合预测模型与方法创新及其优化理论研究”(12BTJ008); 安徽财经大学研究生科研创新基金资助项目(ACYC2015081)

通讯作者:杨桂元(1957-), 男, 安徽萧县人, 教授, 主要从事数量经济学研究. E-mail: yangguiyuan57@163.com

中图分类号:O224

文献标识码:A

文章编号:1671-6876(2016)02-0114-06