“增强学生发现和提出问题能力”的实践研究

◇张 丹

“增强学生发现和提出问题能力”的实践研究

◇张 丹

《义务教育数学课程标准（2011年版）》（以下简称《标准》）在课程总目标中规定：“通过义务教育阶段的数学学习，学生能：体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力。”这突显了增强学生发现和提出问题能力的重要性。从“分析和解决问题能力”到“发现和提出问题、分析和解决问题能力”，也被看成了《标准》关于课程目标的重大进展之一。发现和提出问题的能力不仅仅有利于学生理解相应的概念和方法，提高解决问题的能力，而且可以提高学生的学习兴趣和学习主动性。特别是发现和提出问题将促进学生创新意识的培养，正如《标准》提出的“学生自己发现和提出问题是创新的基础”。

而在实际教学中，学生发现和提出问题的机会是非常少的。据笔者对某次“公开研讨课”的课堂观察，在12节数学课中竟没有一个鼓励学生提出问题的活动，当然学生在课堂中也没有提出一个自己的真实的问题（也许他们的心中是有的）。如何在给学生相应的时间和空间的基础上，更好地提高学生发现和提出问题能力，是实践研究的重点课题，本文也尝试给出几条教学途径。

一 鼓励学生围绕情境自由地提出问题

有研究表明，学生根据自己的知识建构和自由发挥提出问题是提高问题提出能力的重要策略。在荷兰的“现实数学教育”课程设计与教学中，特别强调学生根据自己的知识建构和自由发挥提出问题。甘扎尔斯[1]（Gonzales，1996）在培养学生问题提出能力的教学设计方面，将“产生一个数学任务”作为一个阶段：为学生提供一个缺少明确的数学任务或数学问题的“数学情境”（如统计图表），要求学生根据其中的信息提示，创造或提出一个问题。

因此，学习活动中要为学生提供丰富的、开放的情境，鼓励学生从中发现和提出问题。笔者曾经在北京市海淀区温泉小学鼓励二至六年级的学生，面对如下甲、乙两个水果店的情境，尽可能多地发现和提出问题。实践表明，各个年级都从多个角度提出了富有现实意义的问题（具体描述见本文的第三部分）。

[案例 1]下面是甲、乙两个商店卖水果的柜台。仔细观察和思考，你能提出哪些数学问题？

回想我们平时的课堂教学，虽然也有鼓励学生从情境中发现和提出问题的活动，但这些活动大多数是为了引出所要学习的知识，所以给出的信息往往是比较少的，而且鼓励学生通过这些信息提出加、减、乘、除的问题，以便引入接下来的加、减、乘、除知识的学习。这样的活动是不利于学生发现和提出问题能力的提高的。

史宁中教授曾指出[2]：“发现问题更多地是指发现了书本上不曾教过的新方法、新观点、新途径以及知道了以前不曾知道的新东西。”发现和提出问题的过程不是一件简单的事情。如果我们的教学限制了学生的思考，不仅仅会妨碍学生发现和提出问题水平的提高，时间久了还可能减弱学生发现和提出问题的兴趣和意识。

二 鼓励学生针对所学习的内容自主地发现和提出问题

在义务教育阶段，首先需要培养学生的是发现和提出问题的意识和习惯。所以，最好的途径是给学生自主提出问题的机会。实际上，当学生面临将要学习的内容时，如果给予充分的思考时间，他们是可以提出不少有价值的问题的。

例如，在对于北京市房山区六年级166名学生的抽样调查中，当学生面对将要学习的“圆柱”这一学习对象，鼓励他们提出自己感兴趣的研究问题时，他们能够提出的有意义的数学问题的数量平均为3.46个[3]，提问涉及的方面排名前三的是：圆柱的测量、圆柱的特征、圆柱与其他图形的关系。特别地，学生还提出了不少新颖性的问题，比如：圆柱有几类？圆柱是由什么图形变化而来的？可以怎么制作圆柱？圆柱有周长吗？如果有，什么是圆柱的周长？为什么它叫作圆柱？如果在圆柱中间刻（截）一个面积最大的图形，会是什么图形？如果一个长方体的表面积和圆柱表面积一样，它们的容积相等吗？

在学习完所学内容后，同样可以鼓励学生提出进一步想要研究的问题。比如，在“质数与合数”内容学习后，教师鼓励学生提出自己想要继续研究的问题。下面就是部分同学提出的“有趣”问题[4]：

（1）学习质数和合数有什么用？

（2）有没有一个办法，能快速地找到质数？

（3）寻找质数有没有公式？

（4）有没有最大的质数？

（5）合数的因数是不是有无限多个？

（6）2与 3差 1，3与 5差 2，5与 7差 2，7与11差4……质数是否有一定的规律？

（7）哥德巴赫猜想研究的是什么？

进一步，为了鼓励学生在学习过程中不断积累和交流提出的问题，不少学校还为学生设计了提问本，在班级中开设了“提问角”。在“提问角”中，学生不仅可以展示自己的问题，还可以阅读并尝试解答他人的问题。有的学校还将学生提出的问题汇总筛选后，设计了“可爱作业”鼓励学生进一步开展研究。

[案例2][5]在六年级“圆”单元后，教师鼓励学生提出想要继续研究的问题。在交流各自问题的基础上，学生确定了如下两个研究问题。

问题1：研究其他推导圆面积公式的方法。

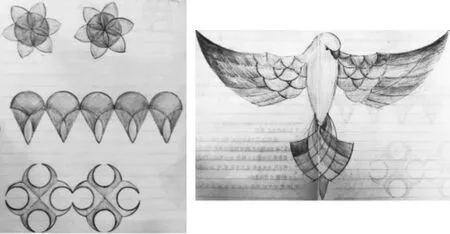
问题2：圆到底有多美？继续用圆设计美丽的图案[6]。

围绕上面的两个问题，学生完成了自己的“可爱作业”。下面是部分学生的作品，虽然有的还需要进一步改进，但无不体现了学生的智慧。

“问题1”的学生作品——推导圆面积公式

“问题2”的学生作品——用圆设计的美丽图案

三 鼓励学生展开联想，联想以前生活经验和学习经验发现和提出问题

在为学生提供了发现和提出问题的活动后，教师往往会遇到这样的困惑：学生提不出问题怎么办？为此，需要采取有效的教学策略，促进他们发现和提出问题能力的提高。

“联想”是促进学生发现和提出更多问题的有效策略。比如，在上面提到的根据甲、乙两个水果店情境提问的案例1中，温泉小学二至六年级所有的班级中，学生都有联想以前的经验来发现和提出问题的意愿。在课堂教学中，学生纷纷提出了自己的“联想”。

生1：把自己想成一个买水果的阿姨。

生2：自己去买水果，你不知道要去哪个商店买，就有疑问了。

师：除了把自己想成买水果的人，还可以把自己想成什么人？

生3：卖水果的人。

生4：还可以把自己想象成一个大水果。（多么宝贵的“童趣”）

带着这些不同角度的联想，经过再次思考，学生纷纷提出了自己的新问题。

生1：一个西瓜10元钱，30元钱能买几个西瓜？

（这个问题看起来是一个简单的计算问题。但实际上这是一个二年级学生提出的问题，此时他还没有学习除法，这是他在教材和平时学习中没有遇到过的问题，但在生活中又是那么常见）

生2：甲商店和乙商店全部的水果一共多少元？

师：为什么要提出这个问题？

生2：我想知道把这两个商店里的水果全卖了，一共能挣多少钱。

生3：甲商店和乙商店各有多少人？我想知道哪个商店更受欢迎。

生4：哪个商店的水果便宜？

生5：综合考虑价钱、质量、路程，妈妈购物要去哪家商店？

生6：1千克苹果进价6元，再考虑租金，售价是多少元才能赚钱？

……

“联想”有效拓展了学生提出问题的角度，“经验”有效提高了学生提出问题的深度和实际意义。联想可以根据以前的生活经验，也可以根据以前学习活动中带来的经验。与此同时，还可以鼓励学生开展反思，不断交流发现和提出问题的其他经验。

四 在解决完一个问题后，鼓励学生利用“what-if-not”方法提出新的问题

布朗和怀特（BrownandWalter，1983）得到提出问题的一个很有用的方法——“否定假设法”（即what-if-not，如果它不是这样的，那又可能是什么样呢）。“这是从原问题出发，产生新问题的非常有效的方法。运用这种策略提出问题有两个关键步骤：首先，列出情境信息的特征；而后是‘what-ifnot’，即学生选择一些特征加以改变来提出问题。”[7]

比如，一位老师首先鼓励学生解决如下问题。

亮亮家、芳芳家和学校的位置如下图。星期天要到学校参加实践活动，他们7时同时从家里出发，7时5分同时到达学校。亮亮从家到学校每分钟走50米，芳芳从家到学校每分钟走40米，亮亮家到芳芳家的距离是多少米？

然后，通过独立思考、合作交流，师生共同整理了上面问题中所包含的信息：同时出发、相对而行、在一条直线上行走、行走的速度、行走的时间、关于相遇的情境等。接着老师提出问题：“你能把其中一个信息进行改变，再提出一个问题吗？”于是学生改变信息，思考“如果不是在一条直线上行走，会怎么样呢”“如果不是相对而行，会怎么样呢”“如果不是同时到达，会怎么样呢”，从而产生了一个又一个新问题。

五 适时鼓励学生对大家提出的问题进行评价，选择自己喜欢的问题

当学生能够发现和提出一定数量的问题后，自然要考虑如何能提出更有价值的问题。考虑到对于小学生，首要的是能打开思路，树立问题意识，不断地发现和提出问题，所以建议教学中不要过于关注问题的价值性，而是在大家自由提出问题的基础上，鼓励学生互相对同伴的问题进行评价，在评价和选择中制定问题是否有价值的“标准”。比如，针对上面提到的案例1，下面是六年级某小组交流的片段。

师:下面开始交流。我们都交流一些什么呢？

生1：我想知道别人提出的问题和我的有什么不同。

师:我们还可以互相讨论，看看哪个问题我们最想研究。

（生2提出的问题是：苹果占梨的百分之几）

生1：是问价格吗？

生2：不是，问的是数量。

生3：是价格还是数量，应提得再明确一些。

生4：可是我们没有必要知道这个问题呀！

师:他提了一个“标准”：关心这个问题有什么用处呀？生2，你能说说吗？

生2：我没想这件事情。

师:生4建议我们提出的问题要有实际意义，生3建议我们提问要尽可能明确。（4个人都表示认同）

按照是否符合实际意义，这个小组的4位同学一共提出了如下几个问题。（按照发言顺序）

①如果西瓜4元1千克，我要买一个3千克的西瓜，要花多少元？

②买2千克苹果的价钱可以买几千克梨？（实际意义是：我就带了这么多钱，要计划一下）

③苹果打八折后，每千克多少元？

④要购买水果，去甲、乙哪个商店更便宜？

⑤考虑价钱、路程、质量等，去哪个商店买更合算呢？

⑥哪家商店的水果质量好一些？

⑦只买苹果，哪个商店的价格比较便宜？

师:现在有7个问题，我们讨论一下最喜欢的问题和理由。

生4：我不喜欢问题①，太简单了。

生1：没有挑战性。

师:我们现在有了衡量好问题的三个标准：第一，要有实际意义；第二，要尽量明确；第三，要具有挑战性。

按照这三个标准，学生共同喜欢的问题是④和⑤。

生1：我喜欢问题⑤，解决这个问题有点紧张和兴奋。

生4：我觉得⑤更难。

通过小组交流，学生已经初步形成了衡量好问题的三个标准。

六 设计专门的活动，鼓励学生发现和提出问题

《标准》中指出：“综合与实践是一类以问题为载体、以学生自主参与为主的学习活动。”发现、选择可以研究的问题并清晰地加以表述无疑是其中重要的一环。因此，教师可以鼓励学生通过自主发现、小组甄选、讨论分析、清晰表述等过程，从生活中、从学习中发现和提出具有挑战性的问题。当然，开始时学生发现的问题往往是模糊的、不完整的，这就需要经历一个“形成问题”的过程。在后面的文章《鼓励学生经历“形成问题”的过程——“反弹高度”的教学实践》中，将展示一位老师引领学生共同经历完善问题、问题分类、推荐问题的过程。

教师还可以安排一些专门的活动，鼓励学生思考并讨论：自己提出的问题是什么意思？什么是一个合理的问题？什么是一个数学问题？一个问题的基本结构是什么？大家所提的问题有几类？你是怎样想到这个问题的？是什么启发了你？鼓励学生积累发现和提出问题的经验。

总之，关于如何增强学生发现和提出问题的能力，还有许多问题需要我们深入思考和实践。尽管我们已经寻找出了部分教学途径和策略，但还需要设计整体的方案，并开展教学实验研究，以检验方案实施的效果。

和注释：

[1]Nancy A.Gonzales．A Blueprint for Problem Posing[J].School Science and Mathematics，1998（8）：448－456.

[2]史宁中，柳海民.素质教育的根本目的与实施路径[J].教育研究，2007（8）：10－14.

[3]有关结论摘自2012年北京市市级学科带头人与骨干教师培训项目成果：房山区小学生在数学学习中提出问题的现状与对策研究。作者:武维民、高冬梅、姚颖、张艳、刘金玲，指导教师：张丹。

[4]这些问题来源于北京大学附属小学李宁老师的研究课“质数与合数”。

[5]该案例来源于中国人民大学附属小学的“可爱作业”。

[6]虽然问题2还不完全具有问题的形态，但作为学生感兴趣的研究活动还是有价值的。

[7]李祥兆.数学问题提出的实证研究述评[J].数学教育学报，2005（11）.

【本文为北京市教育科学“十二五”规划2014年度重点课题“儿童数学教育思想理论内涵与实践创新的研究”（课题编号：3002-0016）的研究成果】

（作者单位：北京教育科学研究院儿童数学教育研究所）