暗物质晕和重子物质的自旋、速度剪切场及涡量的相关性分析∗
2016-06-27刘利利1
刘利利1,2†
(1中国科学院紫金山天文台南京210008)
(2中国科学院大学北京100049)
暗物质晕和重子物质的自旋、速度剪切场及涡量的相关性分析∗
刘利利1,2†
(1中国科学院紫金山天文台南京210008)
(2中国科学院大学北京100049)
在宇宙学流体力学模拟的基础上,通过对速度剪切场、涡量与暗物质晕自旋方向的相关性,以及重子与暗物质之间关系的研究,发现:(1)在小于0.2h−1Mpc的尺度上,重子物质涡量与暗物质涡量的差异比较明显;(2)重子物质的涡量与速度剪切张量的相关性比暗物质要强;(3)小质量暗物质晕的自旋方向平行于其所在的纤维结构的方向,而大质量暗物质晕的自旋方向垂直于纤维结构的方向,并且这种相关性的强弱依赖于模拟盒子大小以及模拟精度.这些因素会使暗物质晕自旋与星系自旋之间的关系复杂化,也会对星系自旋方向与大尺度环境的相关性产生影响.
宇宙学:暗物质,宇宙大尺度结构,方法:数值,统计
1 引言
宇宙学数值模拟和星系红移巡天都显示宇宙在大尺度物质分布上呈网状结构,它由团状(cluster)、纤维(filament)、薄片(sheet)和空洞(void)4种几何构型组成[1].大尺度环境对暗物质晕和星系的演化起着重要的作用[2−3].在过去的20 yr,星系性质与周围环境的关系已被广泛地研究,其中星系自旋方向与纤维和薄片结构的相关性就是一个重要的研究内容.
在星系角动量起源的研究中,最为广泛接受的是潮汐力矩理论(tidal torque theory, TTT),它有一个重要的推论[4−5]:星系的自旋方向与潮汐张量之间存在相关性.并且现在已经有很多观测证据证实了这种相关性的存在[6−7].
有一些宇宙学N体模拟的结果显示暗物质晕的自旋方向与其所在纤维结构的方向是垂直的[8−9];另外一些数值模拟则发现小质量暗物质晕的自旋方向与其所在纤维结构的方向是平行的,而大质量暗物质晕的自旋方向与其所在纤维结构的方向则是垂直的[10−11],并且他们认为,暗物质晕的自旋方向在非线性时期的演化分为两个阶段:(1)小质量的暗物质晕主要通过吸积周围物质形成,所以自旋方向平行于其所在纤维结构的方向;(2)大质量的暗物质晕主要是由小质量的晕沿着纤维结构的方向并合形成,所以大质量暗物质晕的自旋方向垂直于纤维结构的方向.Libeskind等[12]利用宇宙学N体模拟研究发现这种平行和垂直关系的转折质量Mtr是与暗物质晕所处环境有关的, Aragon-Calvo等[10]的研究结果显示在主纤维结构中,Mtr∼1.5×1012M⊙,而在次纤维结构中,Mtr∼4×1011M⊙.另外,Zhang等[9]发现暗物质晕的自旋方向与薄片结构的法向量方向是垂直的.Libeskind等[12]在研究了暗物质晕的自旋方向与涡量的相关性后,发现暗物质晕的自旋方向与涡量方向有很强的平行关系.
近年有一些研究通过宇宙学流体模拟分析了星系特征与周围环境的相关性[13−15]. Dubois等[15]的研究发现小质量星系的自旋方向倾向于平行纤维结构的方向,而大质量星系的自旋方向倾向于垂直纤维结构的方向,他们的结果与N体模拟中得出的暗物质晕的结果一致,都符合自旋方向演化分为两个阶段的假设.Laigle等[14]的数值模拟结果也显示,在大于0.39h−1Mpc的尺度上,涡量与纤维结构的方向是趋于平行的,且暗物质晕的自旋方向与涡量的方向也是趋于平行的.
同时,有很多观测方面的工作也探讨了星系的自旋方向与周围大尺度环境的相关性[6,16−22],在这些研究中都发现了一些平行和垂直的关系.Tempel等[23]基于SDSS(Sloan Digital Sky Survey)观测样本研究了星系自旋与周围环境的相关性,他们发现椭圆星系的自旋(短轴)方向与纤维结构的方向是垂直的,而漩涡星系的自旋方向与纤维结构的方向有很弱的平行关系(在他们的工作中,由于确定椭圆星系的自旋方向非常困难,所以用短轴方向代替椭圆星系的自旋方向).他们还发现星系的自旋方向与薄片结构平面法向量的方向没有相关性,这与数值模拟得到的结果有些许出入.Lee等[24]利用2MASS(The Two Micron All-Sky Survey)红外巡天以及SDSS DR7的数据,研究了星系自旋方向与涡量的相关性,他们计算发现星系自旋方向与涡量有相关性的置信水平为99.9999%.
对于无碰撞的暗物质粒子,涡量的产生是壳交叉(shell crossing)的结果;重子物质的涡量是由气体的可压缩性和斜压性共同决定的[25].气体的可压缩性与速度的剪切张量和速度的散度有关,而气体的斜压性可以快速地放大涡量,尤其是物质在流向薄片、纤维和团状结构时产生的激波周围.这篇文章的主要目的是为了更好地理解暗物质晕、星系与周围环境的关系,为了达到这一目的,我们研究了暗物质晕的自旋方向、潮汐张量、速度剪切场以及涡量之间的相互关系.在第2节,我们介绍了所使用的数值模拟数据及研究方法,第3节中展示了我们得到的结果,总结和讨论在第4节.
2 模拟样本及计算方法
2.1 模拟样本
本文中我们采用了两组暗物质-重子流体混合型的数值模拟样本,模拟盒子尺寸为25h−1Mpc和100h−1Mpc,分别标记为L025和L100样本.数值模拟使用WENO (weighted essentially non-oscillatory)算法进行理想流体力学计算,引力计算则使用标准的PM(particle mesh)方法[26].宇宙学参数采用WMAP5(Wilkinson Microwave Anisotropy Probe 5)的结果:Ωm=0.274,ΩΛ=0.726,h=0.705,σ8=0.812,Ωb=0.0456,ns=0.96.两组模拟都包含10243个暗物质粒子,格点分辨率L100样本为97.7h−1kpc、L025样本为24.4h−1kpc;对暗物质的质量分辨率,L100样本为8.3×107M⊙、L025样本为1.3×106M⊙;数值模拟由初始红移为z=99演化到现在时刻z=0.为考虑宇宙中的再电离过程,我们在红移z=11.0时引入一个均匀的UV背景,但模拟中未引入恒星形成及其反馈.
我们采用FOF(friends-of-friends)方法[27]识别暗物质晕,链接长度取为粒子间平均距离的0.2倍,识别出的暗物质晕平均密度约为宇宙平均密度的180倍.
2.2 计算方法
潮汐张量由下式给出:

其中ϕgrav是引力势,通过泊松方程给出:

速度剪切场的计算公式如下:
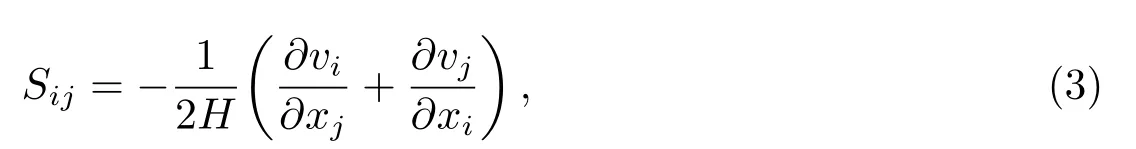
式中的H是哈勃常数,负号使得正的特征值对应于压缩流.速度剪切场的3个特征值标记为λ1>λ2>λ3,对应的特征向量分别为e1,e2,e3.
涡量为速度场的旋度:

我们将暗物质和重子物质的密度和速度用CIC(cloud in cell)方法分配到5123个格点上,取平滑尺度Rf=0.2h−1Mpc进行平滑,在每一个格点上计算潮汐张量、速度剪切张量和涡量,并且计算潮汐张量、速度剪切张量的特征值和特征向量.
2.3 宇宙网状结构的分类方法
为了对宇宙网状结构进行分类,我们计算了速度剪切张量.速度剪切张量的3个特征值记为:λ1>λ2>λ3,对应的特征向量分别为:e1,e2,e3.沿用Ho ff man等[28]给出的优化结果,取特征值的阈值λth=0.6,通过判断大于给定阈值的特征值个数可以将宇宙网状结构按以下判据划分:团状结构:λ1>λ2>λ3>λth,纤维结构:λ1>λ2>λth>λ3,薄片结构:λ1>λth>λ2>λ3,空洞结构:λth>λ1>λ2>λ3.
3 结果分析
为了研究潮汐张量、速度剪切张量与涡量之间的相关性,我们计算了概率分布函数p(|cosµ|),其中µ是两个方向之间的夹角,|cosµ|的取值范围为[0,1].当|cosµ|=1时,两个方向相互平行,|cosµ|=0则相互垂直;p(|cosµ|)代表夹角余弦绝对值的分布函数.
3.1 重子物质与暗物质的对比
为了比较重子物质与暗物质的性质,我们计算了暗物质和重子物质的涡量,分别记为ωd,ωb;暗物质的剪切张量的3个特征向量记为e1d,e2d,e3d,重子物质的剪切张量的3个特征向量记为e1b,e2b,e3b;暗物质的潮汐张量的3个特征向量记为t1d,t2d,t3d,重子物质的潮汐张量的3个特征向量记为t1b,t2b,t3b.
我们分别计算了暗物质涡量与重子物质涡量的夹角,即ωd与ωb的夹角;暗物质剪切张量与重子物质剪切张量的夹角,即e1d与e1b,e2d与e2b,e3d与e3b的夹角;暗物质潮汐张量与重子物质潮汐张量的夹角,即t1d与t1b,t2d与t2b,t3d与t3b的夹角.
图1给出了重子物质与暗物质相关性的概率分布函数,分别对应重子物质与暗物质潮汐张量的特征向量的相关性、速度剪切场之间的相关性,以及涡量的相关性.从图上我们可以看出,对于潮汐力场和速度剪切场,重子物质与暗物质的方向几乎完全一致.这是由于重子物质的密度增长主要是由暗物质主导的,因为宇宙中暗物质的质量比重更大,潮汐力场正是反映了密度场的性质,所以重子物质与暗物质的潮汐力场几乎完全一致.对于速度剪切场,在线性和非线性演化阶段,速度场都主要是由密度场主导的,所以也出现了重子物质与暗物质的速度剪切场几乎一致的情况.另一方面,重子物质与暗物质中涡量的一致性相对较弱,夹角余弦值的平均值为0.83.
图2所示的是平滑尺度对重子物质涡量和暗物质涡量相关性的影响.显然,重子物质涡量与暗物质涡量的差异随平滑尺度的增加而减小,当平滑尺度Rf=0.2h−1Mpc时,角余弦的平均值为cosµ≃0.83,当平滑尺度增加到Rf=1.6h−1Mpc,余弦的平均值为cosµ≃0.93.
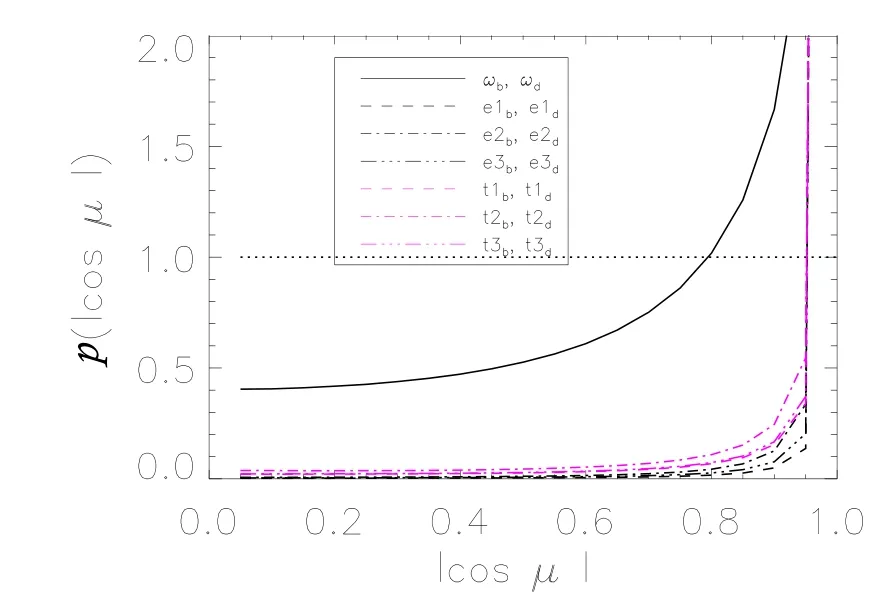
图1 重子物质与暗物质的潮汐张量、速度剪切场以及涡量之间夹角余弦绝对值|cosµ|的概率分布函数Fig.1 The probability distribution as a function of|cosµ|with the angels determined by the tidal tensor,velocity shear,and vorticity of baryonic and dark matter
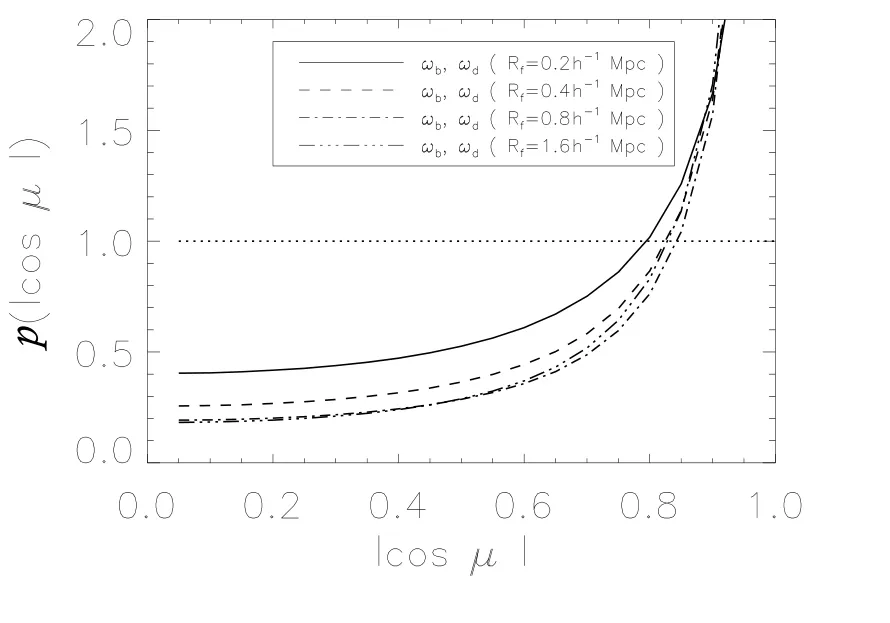
图2 平滑尺度对重子物质涡量和暗物质涡量夹角余弦绝对值|cosµ|的概率分布函数的影响Fig.2 The effect of smooth length on the probability distribution of|cosµ|with the angels determined by the vorticity of baryonic and dark matter
图3所示的是在宇宙网络的不同结构中重子物质涡量与暗物质涡量的相关性.当红移z=0时,在团状结构、纤维结构和薄片结构中的相关性都很接近,比在空洞结构中的相关性更强一些.这是因为在空洞结构中,暗物质粒子的数目非常少,给计算暗物质速度场带来偏差,可能在计算中引入额外的误差.同时由于团状结构所占的体积比很小,也可能会给统计带来很大的弥散,造成计算结果的误差.在红移z=0,1,2时,余弦的平均值都在0.9左右,随着红移的演化,相关性减弱得非常慢.
图4给出了模拟盒子大小和模拟精度对暗物质涡量与重子物质涡量相关性的影响.从图中我们可以看出,L025模拟中相关性比L100更弱.对L025样本,取平滑尺度Rf=0.05h−1Mpc时,⟨cosµ⟩≃0.62;而当Rf=0.20h−1Mpc时,⟨cosµ⟩≃0.75.由于重子物质的涡量由可压缩性和斜压性共同决定,因此在演化过程中,当压力相对于引力不可被忽略时,斜压将会驱动重子物质的涡量,并偏离暗物质的涡量分布,使得出现图中所示的结果.另一方面,更高分辨率的模拟可能会抑制数值粘滞,从而引起重子物质涡量的增长,也使得重子物质的涡量更显著偏离暗物质,所以在L025样本中,涡量的相关性会更弱一些.
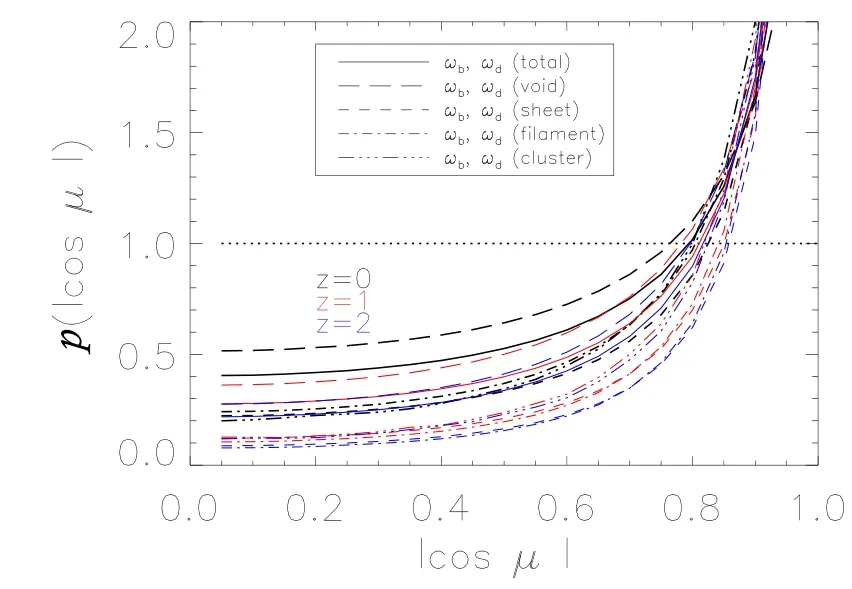
图3 重子物质的涡量与暗物质涡量夹角余弦绝对值|cosµ|的概率分布函数在不同的宇宙网络结构中的分布.黑色、红色、蓝色线分别对应红移z=0,1,2.Fig.3 The probability distribution as a function of|cosµ|with the angle determined by the vorticity of baryonic and dark matter in di ff erent large-scale structures at z=0(black line),1(red line),and 2(blue line)
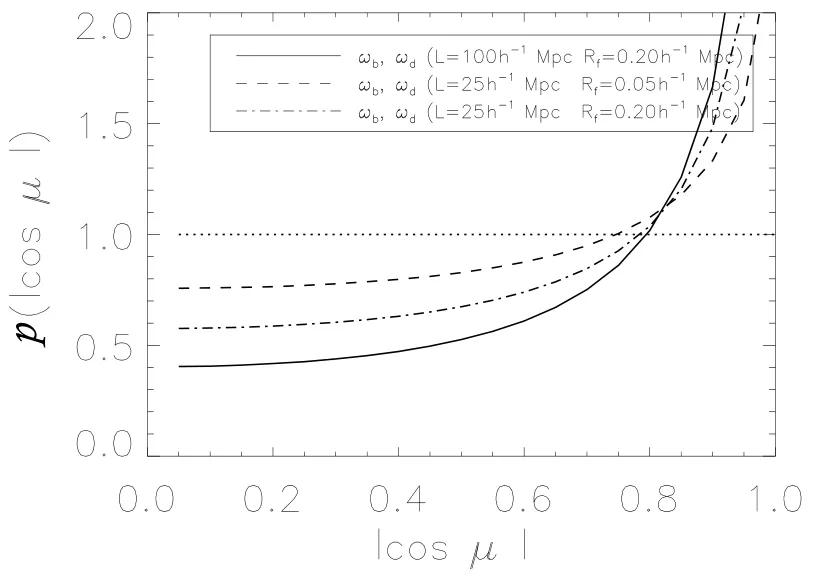
图4 模拟盒子大小以及模拟精度对重子物质的涡量与暗物质涡量夹角余弦绝对值|cosµ|的概率分布函数的影响Fig.4 The effect of box size and simulation resolution on the probability distribution of |cosµ|with the angle determined by the vorticity of baryonic and dark matter
3.2 涡量与速度剪切场的相关性
图5中所示的是涡量的方向分别与速度剪切张量的3个特征向量的相关性.图中水平点线代表均匀分布.如我们在图中所看到的那样,暗物质的速度剪切张量的特征向量e1d与暗物质的涡量ωd的方向是趋于垂直的,而e2d与ωd的方向是趋于平行的, e3d与ωd的方向也是趋于平行的.根据定义,速度剪切张量大于0的特征值对应的特征向量的方向是物质聚集的方向,所以,暗物质涡量的方向与暗物质最聚集的方向是趋于垂直的,这与Libeskind等人2013年的结果[29]相一致.同时从图中我们可知,重子物质的情况与暗物质的情形是相似的,也就是e1b与ωb的方向是趋于垂直的,而e2b与ωb的方向则是趋于平行的,e3b与ωd的方向也是趋于平行的.此外,如果在计算涡量和速度剪切场时,当平滑尺度选择Rf=0.8h−1Mpc时,相关性会比Rf=0.2h−1Mpc时有所减弱;同时在L025的样本中,暗物质与重子物质的差别会更大一些.
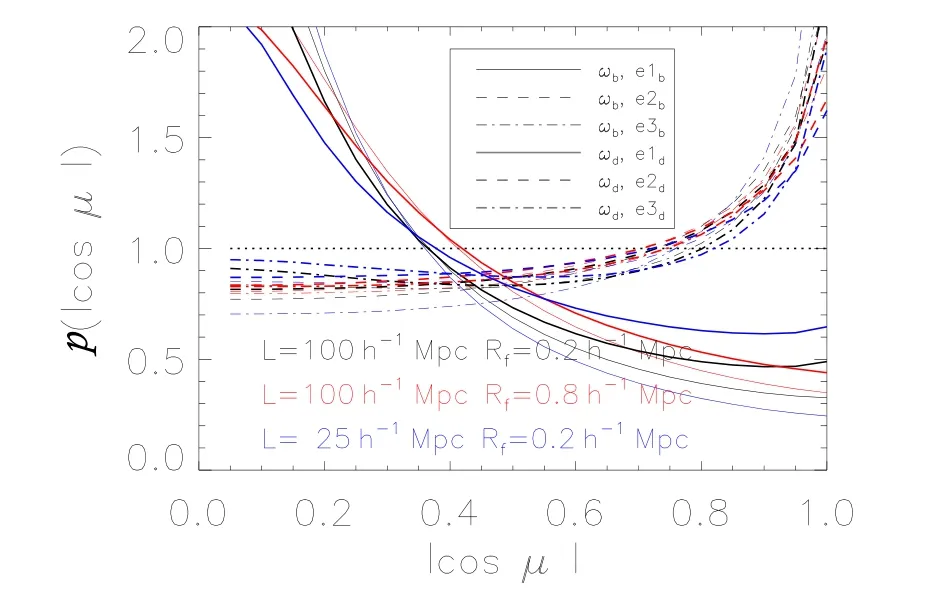
图5 重子物质、暗物质的涡量与速度剪切张量夹角余弦绝对值|cosµ|的概率分布函数.黑色的线对应样本L100,平滑尺度Rf=0.2h−1Mpc;红色的线对应样本L100,Rf=0.8h−1Mpc;蓝色的线对应样本L025,Rf=0.8h−1Mpc. Fig.5 The probability distribution as a function of|cosµ|with the angles determined by the vorticity and the eigenvectors of the shear tensor in baryonic and dark matter.Black lines correspond to L100 with smooth length Rf=0.2h−1Mpc,red lines correspond to L100 with Rf=0.8h−1Mpc,and blue lines correspond to L025 with Rf=0.8h−1Mpc.
图6给出了L100样本分别在团状、纤维、薄片和空洞结构中,暗物质的涡量方向与暗物质的速度剪切张量的特征向量的相关性.从图中我们可以看出,当物质从薄片结构向纤维结构和团状结构中聚集的过程中,相关性在逐渐变弱.与图6类似,图7中所示的是L100样本分别在不同结构中,重子物质的涡量方向与重子物质的速度剪切场的特征向量的相关性.容易看出,重子物质的相关性与暗物质的相关性是相似的.
3.3 暗物质晕的自旋与速度剪切场的相关性
暗物质晕自旋的计算方法是:
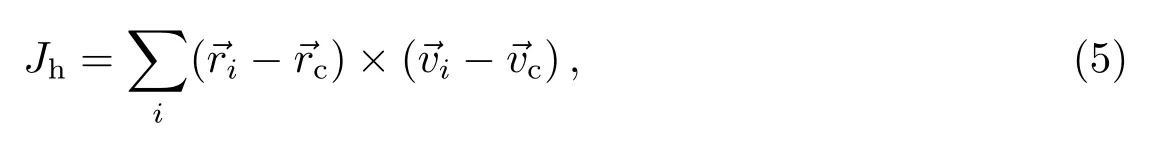
式中的下标i表示暗物质晕中的第i个粒子,rc表示暗物质晕的中心位置,vc是暗物质晕的整体速度,也就是暗物质晕中所有粒子的平均速度.
在L100样本中,我们把暗物质晕分成3个质量区间,分别为(1010−1011)M⊙,(1011−1012)M⊙,(1012−1013)M⊙.在每一个质量区间里面,相关性的强弱我们用偏离均匀分布的平均偏差来表示.
Libeskind等[29]和Lee等[24]通过数值模拟研究得出了一致的结论,即暗物质晕的角动量J与速度剪切张量的特征向量e3d的方向,对小质量暗物质晕是趋于平行的,而在大质量端则趋于垂直.在宇宙大尺度环境中,速度剪切张量的特征向量e3的方向与纤维结构的方向是一致的,即小质量的暗物质晕的自旋方向是趋于平行于其所在的纤维结构方向的,而大质量的暗物质晕的自旋方向是趋于垂直于其所在纤维结构方向的.
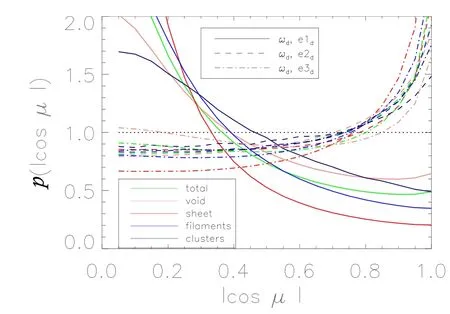
图6 暗物质的涡量与速度剪切场夹角余弦绝对值|cosµ|的概率分布函数在不同结构中的分布.黑色、蓝色、红色及粉红色线分别对应团状、纤维、薄片及空洞结构.Fig.6 The probability distribution as a function of|cosµ|with the angles determined by the dark matter vorticity and the eigenvectors of the shear tensor in di ff erent structures.Black,blue,red,and pink lines correspond to cluster, filament,sheet, and void structures,respectively.
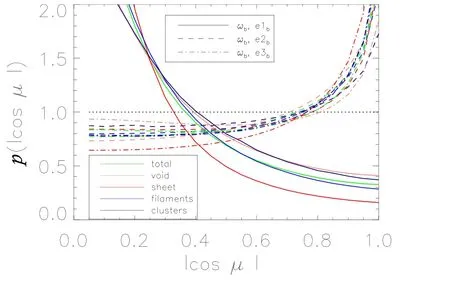
图7 同图6.不同的是图6是暗物质中概率分布函数,而图7是重子物质中的概率分布函数.Fig.7 Same as Fig.6.The di ff erence is that the probability distribution in dark matter is shown in Fig.6,while the probability distribution function in baryonic matter is shown in Fig.7.
图8中所示的是暗物质晕的角动量J与速度剪切张量的3个特征向量的方向e1d、e2d、e3d的相关性,黑色线对应暗物质晕的质量区间为(1010−1011)M⊙,绿色线对应暗物质晕的质量区间为(1011−1012)M⊙,红色线对应暗物质晕的质量区间为(1012−1013)M⊙.两个方向平行的程度由偏离均匀分布的平均偏差<σ>给出,以泊松误差为单位.从图中我们可以看出,我们的结果与前人的结果是一致的,也就是,小质量暗物质晕的自旋方向平行于其所在纤维结构的方向,而大质量暗物质晕的自旋方向垂直于其所在纤维结构的方向.
图9和图8所示的内容相近,它展示了暗物质晕角动量J与速度剪切张量的3个特征向量的方向e1d、e2d、e3d的相关性,黑色线对应暗物质晕的质量区间为(1010−1011)M⊙,绿色线对应的质量区间为(1011−1012)M⊙,红色线为(1012−1013)M⊙.区别是图8中的平滑尺度Rf=0.2h−1Mpc,而在图9中平滑尺度则取Rf=0.8h−1Mpc,从图中我们可以看出,平滑尺度Rf=0.8h−1Mpc时,相关性相对要弱,尤其在(1011−1012)M⊙和(1012−1013)M⊙质量区间这种减弱较为明显.
图10绘出了L025样本的统计结果,黑色线对应暗物质晕的质量区间为(109−1010)M⊙,绿色线对应的质量区间为(1010−1011)M⊙.在这个样本中,由于模拟盒子小,大质量的暗物质晕的数量相对较少,我们把暗物质晕的质量区间分为: (109−1010)M⊙和(1010−1011)M⊙.显然,对于L025样本,相关性不是很明显.
通过图8、图9和图10的比较可以看出,暗物质晕的自旋与暗物质速度剪切张量的相关性,对平滑尺度和模拟的盒子大小很敏感.
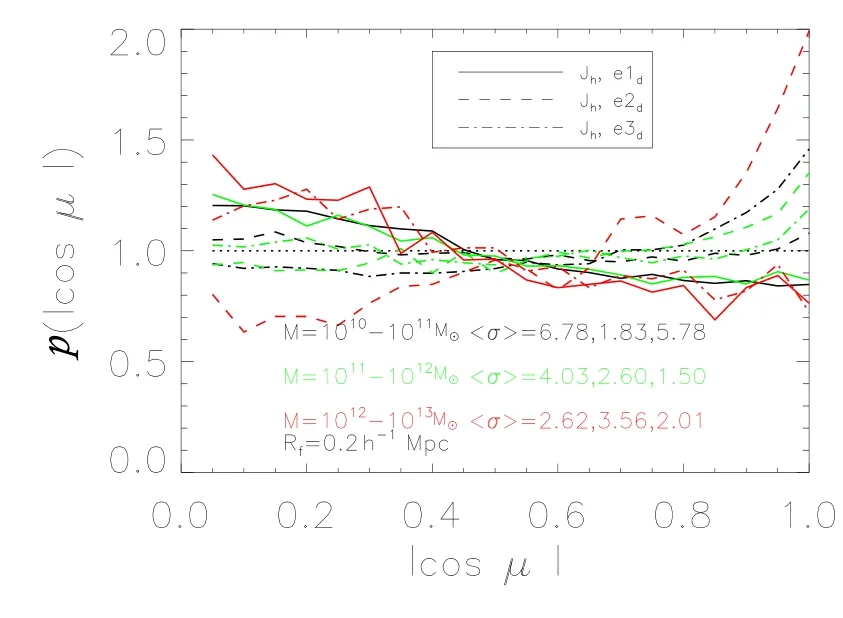
图8 暗物质晕的自旋与速度剪切张量夹角余弦绝对值|cosµ|的概率分布函数.在L100样本中,取平滑尺度Rf=0.2h−1Mpc.Fig.8 The probability distribution as a function of|cosµ|with the angels determined by the spin of dark matter halos and eigenvectors of shear tensor in the simulation L100,with smooth length Rf=0.2h−1Mpc
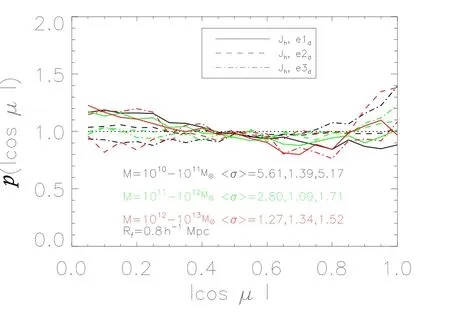
图9 同图8,取平滑尺度Rf=0.8h−1MpcFig.9Same as Fig.8,but with smooth length Rf=0.8h−1Mpc
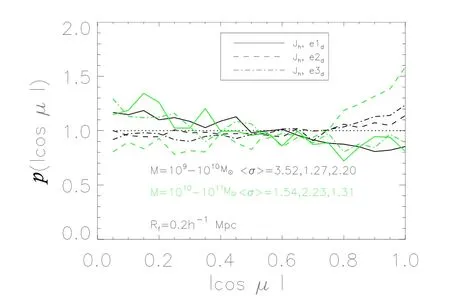
图10 暗物质晕的自旋与速度剪切张量的特征向量夹角余弦绝对值|cosµ|的相关性概率分布函数.在L025样本中,取平滑尺度Rf=0.2h−1Mpc.Fig.10 The probability distribution as a function of|cosµ|determined by the spin of dark matter halos and eigenvectors of shear tensor in the simulation L025,with smooth length Rf=0.2h−1Mpc
3.4 暗物质晕的自旋与涡量的相关性
此外,我们还研究了暗物质晕的自旋与涡量的相关性.我们同样把L100样本中的暗物质晕的质量区间分为:(1010−1011)M⊙,(1011−1012)M⊙和(1012−1013)M⊙,L025样本的暗物质晕的质量区间分为:(109−1010)M⊙和(1010−1011)M⊙.
图11和图12比较了不同暗物质晕质量区间自旋与涡量的相关性,图11是L100样本的结果,绿色线对应暗物质晕的质量区间为(1010−1011)M⊙,红色线代表(1011−1012)M⊙,蓝色线代表(1012−1013)M⊙;图12是L025样本的结果,绿色线对应暗物质晕的质量区间为(109−1010)M⊙,红色线为(1010−1011)M⊙.在这两个模拟样本中,平滑尺度约为暗物质晕维里半径的4倍.这个结果也与Libeskind等[29]得到的结果一致,即暗物质晕的自旋与涡量的方向是趋于平行的.
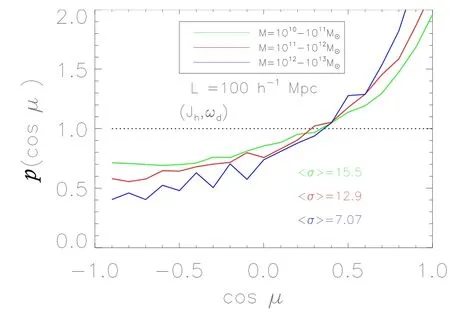
图11 L100样本中暗物质晕的自旋与涡量夹角余弦绝对值|cosµ|的概率分布函数Fig.11 The probability distribution as a function of|cosµ|with the angle determined by the spin and vorticity of dark matter halos in the simulation L100
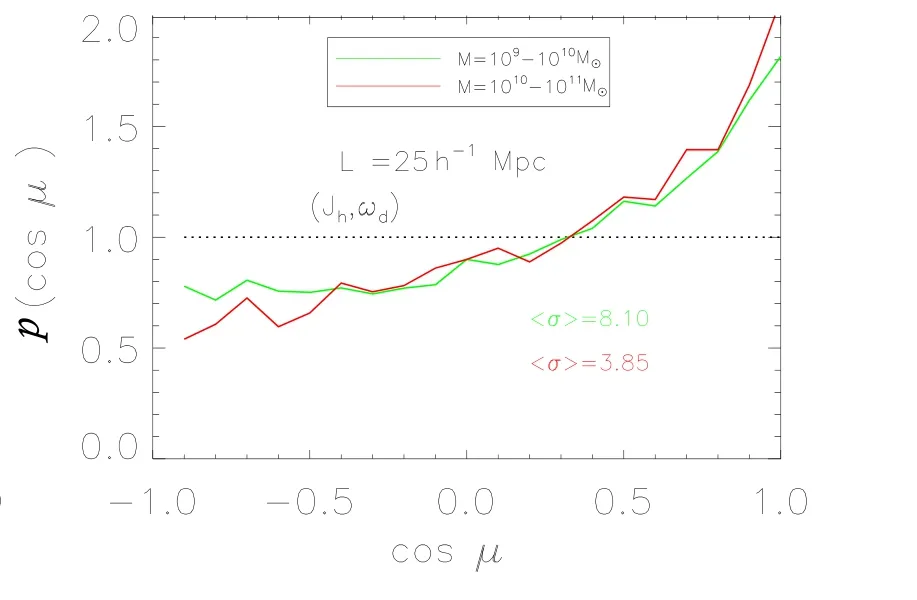
图12 同图11,不同的是在样本L025中Fig.12Same as Fig.11,but in the simulation L025
3.5 暗物质晕的自旋与晕内重子物质角动量的相关性
由于通常宇宙学数值模拟给出的结果都是暗物质晕的自旋,而实际观测中得到的是星系的自旋,因此我们希望可以得到暗物质晕的自旋方向与星系的自旋方向的关系.但是我们的模拟不包含恒星形成及其反馈,无法描述星系的性质.不过我们仍然可以简单地对比暗物质晕的自旋与暗物质晕里面的重子物质的角动量的关系.
我们选取半径大于2倍模拟网格大小的暗物质晕,在L100样本中有1330个暗物质晕;在L025样本中,有1031个暗物质晕.图13和图14展示的是在这两个模拟样本中,暗物质晕的自旋与所包含重子物质的角动量的关系.两个不同模拟精度的样本结果是相似的,暗物质晕的自旋与晕内重子物质的角动量的方向是趋于平行的.
4 小结
运用宇宙学数值模拟的方法,我们研究了潮汐张量、速度剪切张量、涡量、暗物质晕自旋方向之间的相关性,并且对重子物质和暗物质的性质做了对比.我们得到的主要结果有:
(1)重子物质的潮汐张量和速度剪切张量的特征向量是分别与暗物质平行的,而重子物质的涡量方向与暗物质的涡量方向在小于等于0.2h−1Mpc尺度上存在较大的差异.对于L100样本,重子物质涡量与暗物质涡量的夹角余弦绝对值的平均值约为0.83;对于L025样本,重子物质涡量与暗物质涡量的夹角余弦绝对值的平均值约为0.75.
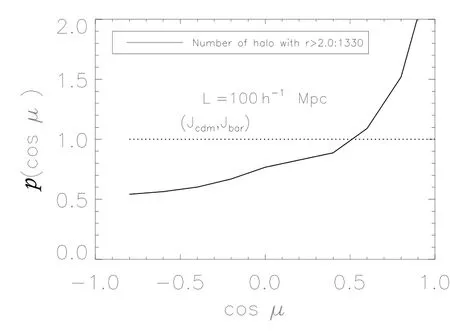
图13 样本L100中,暗物质晕的自旋与晕里面重子物质角动量夹角余弦绝对值|cosµ|的概率分布函数.为了计算的精确度,我们取暗物质晕的半径>0.2h−1Mpc,即大于两个格子大小.Fig.13 The probability distribution as afunction of the angle determined by the spin of dark and baryonic matter halos with a radius larger than 0.2h−1Mpc in the simulation L100
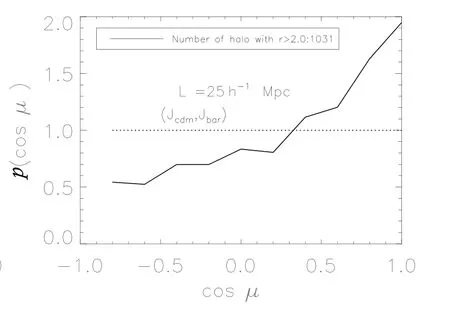
图14 同图13,不同的是在样本L025中Fig.14Same as Fig.13,but in the simulation L025
(2)涡量的方向ω与速度剪切张量的特征向量e1的方向趋于垂直,而ω与e2和e3都是趋于平行的,并且重子物质的相关性比暗物质要稍微强一些.平滑尺度对相关性的强弱也有影响,当取更大的平滑尺度时,相关性变弱.涡量与速度剪切场的相关性与大尺度环境也有关系,在高密度的团状结构中,探测到的信号更弱一些,而在纤维和薄片结构中信号则表现得更强一些.
(3)小质量的暗物质晕自旋方向更趋于平行于晕所在的纤维结构的方向,而大质量的暗物质晕的自旋方向更趋于垂直于所在纤维结构的方向,并且这种相关性的强弱依赖于平滑尺度和模拟精度,当取更大的平滑尺度和提高模拟精度时,相关性变弱.
(4)暗物质晕的自旋方向与晕内重子物质的角动量的方向总是趋于平行的.
从整体来看,重子物质与暗物质的涡量方向在小于等于0.2h−1Mpc尺度上存在的差异可能会使得暗物质晕的角动量方向与气体的旋涡运动的关系更为复杂.另一方面,小质量的暗物质晕的自旋与周围环境的关系更密切,而大质量晕的自旋更依赖于晕和晕之间的相互作用.同时,宇宙网络结构的分类方法、模拟精度等因素都会给相关信号带来影响,加上我们的模拟不包含恒星形成及其反馈,这些都使所获得的相关信号具有一定的不确定性.
[1]Bond Nicholas A,Strauss M A,Cen R.BAAS,2006,38:966
[2]White S D M.ApJ,1984,286:38
[3]Aragon-Calvo M A,van de Weygaert R,Jones B J T,et al.ApJ,2007,655:L5
[4]Porciani C,Dekel A,Ho ff man Y.MNRAS,2002,332:325
[5]Porciani C,Dekel A,Ho ff man Y.MNRAS,2002,332:339
[6]Lee J,Erdogdu P.ApJ,2007,671:1248
[7]Sch¨afer B M.IJMPD,2009,18:173
[8]Hahn O,Porciani C,Carollo C M,et al.MNRAS,2007,375:489
[9]Zhang Y,Yang X,Faltenbacher A,et al.ApJ,2009,706:747
[10]Aragon-Calvo M A,Yang L F.MNRAS,2014,440:L46
[11]Codis S,Pichon C,Devriendt J,et al.MNRAS,2012,427:3320
[12]Libeskind N I,Ho ff man Y,Knebe A,et al.MNRAS,2012,421:L137
[13]Hahn O,Teyssier R,Carollo C M.MNRAS,2010,405:274
[14]Laigle C,Pichon C,Codis S,et al.MNRAS,2015,446:2744
[15]Dubois Y,Pichon C,Welker C,et al.MNRAS,2014,444:1453
[16]Trujillo I,Carretero C,Patiri S G.ApJL,2006,640:L111
[17]Paz D J,Stasyszyn F,Padilla N D.MNRAS,2008,389:1127
[18]Jones B J T,van de Weygaert R,Aragon-Calvo M A.MNRAS,2010,408:897
[19]Cervantes-Sodi B,Hernandez X,Park C.MNRAS,2010,402:1807
[20]Andrae R,Jahnke K.MNRAS,2011,418:2014
[21]Varela J,Betancort-Rijo J,Trujillo I,et al.ApJ,2012,744:82
[22]Zhang Y,Yang X,Wang H,et al.ApJ,2013,779:160
[23]Tempel E,Libeskind N I.ApJL,2013,775:L42
[24]Lee J H,Rey S C,Kim S.ApJ,2014,791:15
[25]Zhu W S,Feng L L,Fang L Z.ApJ,2010,712:1
[26]Feng L L,Shu C W,Zhang M P.ApJ,2004,612:1
[27]Davis M,Efstathiou F,Frenk C S,et al.ApJ,1985,292:371
[28]Ho ff man Y,Metuki O,Yepes G,et al.MNRAS,2012,425:2049
[29]Libeskind N I,Ho ff man Y,Steinmetz M,et al.ApJL,2013,766:L15
Correlation Analysis between Spin,Velocity Shear, and Vorticity of Baryonic and Dark Matter Halos
LIU Li-li1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
(2 University of Chinese Academy of Sciences,Beijing 100049)
Using cosmological hydrodynamic simulations,we investigate the alignments between velocity shear,vorticity,and the spin of dark matter halos,and study the correlation between baryonic and dark matter.We find that(1)mis-alignment between vorticity of baryonic and dark matter would develop on scales<0.2h−1Mpc; (2)the vorticity of baryonic matter exhibits stronger alignment/anti-alignment with the eigenvectors of velocity shear than that of dark matter;(3)small/massive halos spinning parallel/perpendicular to the host filaments are sensitive to the identi fication of cosmic web,simulation box size,and resolution.These factors might complicate the connection between the spins of dark matter halos and galaxies,and a ff ect the correlation signal of the alignments of galaxy spin with nearby large-scale structures.
cosmology:dark matter,large-scale structure of Universe,methods:numerical,statistical
P159;
:A
10.15940/j.cnki.0001-5245.2016.03.002
2015-11-13收到原稿,2016-01-05收到修改稿
∗国家自然科学基金项目(Y3GJ161110)资助
†stellvia@hotmail.com
