天体测量方法解算惯导漂移的原理及其模拟∗

齐朝祥郭素芬 于 涌 唐正宏

(1中国科学院上海天文台上海200030)

(2中国科学院大学北京100049)

天体测量方法解算惯导漂移的原理及其模拟∗

齐朝祥1†郭素芬1,2于 涌1唐正宏1

(1中国科学院上海天文台上海200030)

(2中国科学院大学北京100049)

惯性导航系统绕其坐标轴的角度漂移极大地制约着飞行器基于惯导(惯性导航)进行导航的效果.提出了基于天体测量原理纠正惯性导航角度漂移的方法,详述了其实现过程.利用设计的方案及编制的软件进行了模拟实验,模拟数据结果表明:提出的方法能有效地求解并纠正惯性导航系统的角度漂移.

天体测量,参考系,方法:观测

1 引言

惯性导航系统是一种利用加速度计和陀螺仪等惯性元件测量物体的加速度和转动角速度,再经过积分运算求得任意时刻物体的位置、速度和姿态信息的导航设备.惯性导航在设备启动前需要预先注入飞行轨迹及其周围引力场模型的信息,但飞行过程中不再需要外来无线电信息,也不会向外辐射信息,因此是一种完全自主的导航系统.惯性导航系统相比无线电导航、卫星导航等导航系统具有全天候、自主性、隐蔽性、抗辐射、无辐射、可连续工作等特点,已成为最经典的自主导航技术之一.目前在航空、航天、航海等领域均具有广泛应用,尤其在国防建设中具有重要意义,在战时,其在自主性上具有无线电导航所无法比拟的优越性[1−2].

惯性导航系统的最终精度主要取决于加速度计和陀螺仪等惯性元件随时间积累的漂移误差.本文的工作主要涉及与陀螺仪绕轴角度漂移的问题,并不涉及加速度计问题.目前提高惯性导航系统精度的方法主要有两种:一是提高惯性元件的精度;二是检测出漂移量并对其进行纠正.前者需要高精度工艺技术,如目前精度最高的静电陀螺的绕轴漂移率为10−6–10−5degree·h−1[3],但其制作工艺非常难、研发经费高昂且周期长.这种高精度的测量器件国外对我国禁运,目前国内多数惯导陀螺均由自主研发,精度上还难以达到国际领先水平,我国较高精度惯导设备的绕轴角度漂移率多在10−3–10−2degree·h−1的水平.经多方面考虑,采用其他辅助技术来纠偏是更为易行的解决途径.对陀螺漂移直接纠偏又可分为两种情况:一是用惯导系统自身的信息来预报并纠正漂移,如卡尔曼滤波、小波分析等数据分析方法,也可以通过转动调制来补偿陀螺漂移[3],但此类方法均属外推,具有一定的局限性;二是通过引入误差不随时间积累的外部信息对漂移进行纠正,如天文导航.通过天文观测能够得到飞行器在天文惯性坐标系中的姿态参数,结合惯导系统输出的信息,经过一定的标校处理后即可计算出惯导系统的漂移量,两者扬长避短、优势互补,从而最终实现高精度的导航任务要求.并且借助天文手段直接观测恒星不需人为介入也不会向外辐射信息,这与惯导系统对隐蔽性好和自主性强的要求非常吻合,除此之外,天文方法还具有易于实现、精度高且无姿态累积误差、成本低等优点.本文的天体测量方法就属于这类方法.

20世纪60年代以来,在军工领域,将望远镜安装在巡航导弹、洲际导弹、高空飞机等装有惯导系统的运载体上,同时使用光学天文和陀螺仪导航技术进行联合制导已经得到了较为广泛的应用.长久以来,这方面的技术主要被美国和俄罗斯等欧美国家掌握,我国在天文和惯导联合制导方面起步较晚,但目前已取得较大进步,如在某型号空中加油机上已使用自主研发的产品[4],但总体上处于逐步追赶的阶段.

目前,用于惯导的光学天文导航设备多为星敏感器[4–6],这是一种常规的空间飞行器(如人造卫星)姿态测量的光电设备,它视场非常大,可通过单次成像观测到多颗恒星.基于CCD照相相对测量的原理,即可给出每个星敏感器的光轴姿态,安装3个星敏感器即可自主地获得并提供空间飞行器在天文(惯性)参照系下的全部姿态信息.除此之外,也有一些飞行器采用了单个光学望远镜,分多次观测不同恒星或一直监视某颗恒星的方式进行天文导航.光学望远镜较星敏感器的主要优势是焦距比较长,CCD角分辨率高,单次观测的恒星方向定位精度更高,并且观测恒星时更加主动,可以事先设计好航迹上需要检测的恒星,且基本不会遇到星敏感器上容易出现的视场无星或有星但匹配不成功的问题.本文在利用光学望远镜机动指向不同恒星观测方式的基础上,提出了一种基于天体测量方法解算惯导漂移的原理并对实现过程进行了阐述.

2 基本原理

光学天文观测能得到天体相对观测设备本体坐标系的量度坐标,天体在某一时刻某个特定天文(惯性)参考系中的观测方向的高精度坐标可以通过恒星参考星表并经严格的天体测量理论计算得到,由此可以反推观测设备乃至其所在飞行器在天文(惯性)参考系的姿态及其变化信息.飞行器的惯导系统可以输出位置、姿态和速度信息.比较天文观测和惯导系统输出的数据即可解算惯导系统的角度漂移量,进而对其进行纠正.

2.1 基本坐标转换矩阵

设坐标系[P]是由坐标系[S]绕第1轴逆时针旋转θ1而成的,则坐标系[P]中的坐标p= (XP,YP,ZP)T和坐标系[S]中的坐标s=(XS,YS,ZS)T有以下关系:p=R1(θ1)s,其中R1(θ1)为坐标转换矩阵

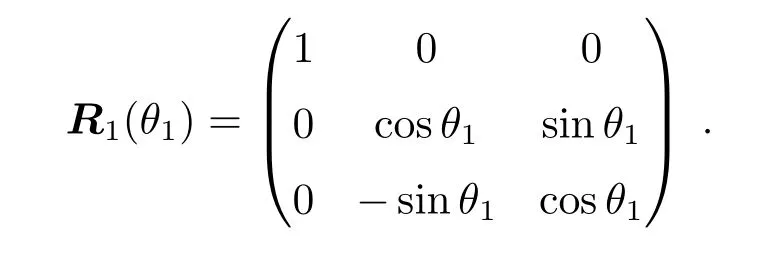
若坐标系[P]是由坐标系[S]绕第2轴逆时针旋转θ2而成的,则转换矩阵为

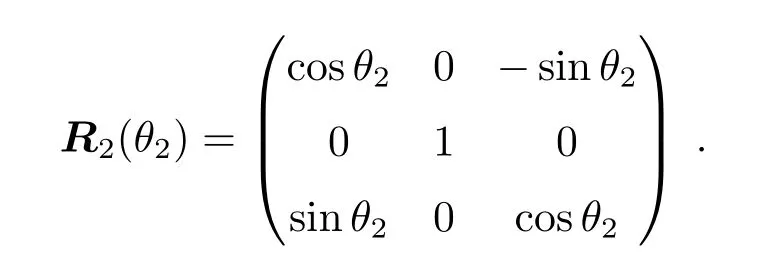
若坐标系[P]是由坐标系[S]绕第3轴逆时针旋转θ3而成的,则转换矩阵为

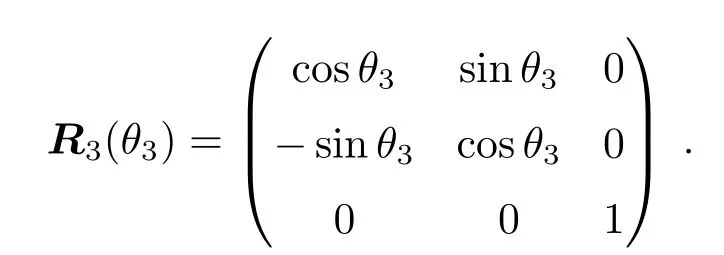
对于任意两个原点相同的直角坐标系,只要将其转换关系分解成几次有序的绕轴旋转,就可以用R1、R2、R3的相应组合来实现坐标转换.

2.2 由惯导系统输出的数据计算坐标转换矩阵

本文涉及的坐标系及其表征符号主要有:运载体本体坐标系[F]、地平参考系[Z]、国际地球参考系[E]和地心天球参考系[G],其中,本文定义的运载体本体坐标系

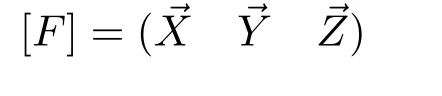
是一种与运载体刚性固连的坐标系.该坐标系的原点与运载体质心重合,第1轴(X轴)沿运载体纵轴指向前,第2轴(Y轴)沿横轴指向左,第3轴(Z轴)沿着竖轴并与第1、2轴构成右手系,如图1所示.当运载体在水平面内沿着子午方向向北飞行时,此坐标系与(本文定义的)当地的地平参考系重合.

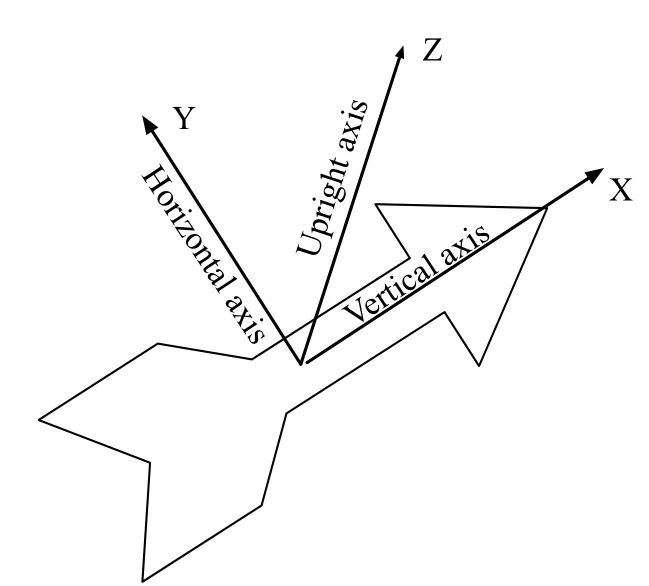
图1 运载体本体坐标系示意图Fig.1 The diagram of the air vehicle body- fixed coordinate system

本文的地平系(地平参考系)定义与常规定义略有不同.具体如下:[Z]表示地平系,其第1和第2轴所在的基本面为当地的水平面,第3轴指向天顶(与铅垂线方向相反).此坐标系中方向矢量的经纬度用(A,H)表示,分别称作方位和高度.这里定义方位的起始点为天文北方,向西为正,按照逆时针方向(北→西→南→东)0◦→360◦度量.这里定义高度向天顶方向为正,按照0◦→±90◦计量,参见图2.国际地球参考系(本文有时简称为地固系,其中XE、YE坐标轴在地球赤道面内,XE坐标轴指向地球零经度起点,ZE指向地球自转轴方向,(λ,φ)为地理经纬度)和地心天球惯性系的定义与国际规范一致[7],在此不做赘述.

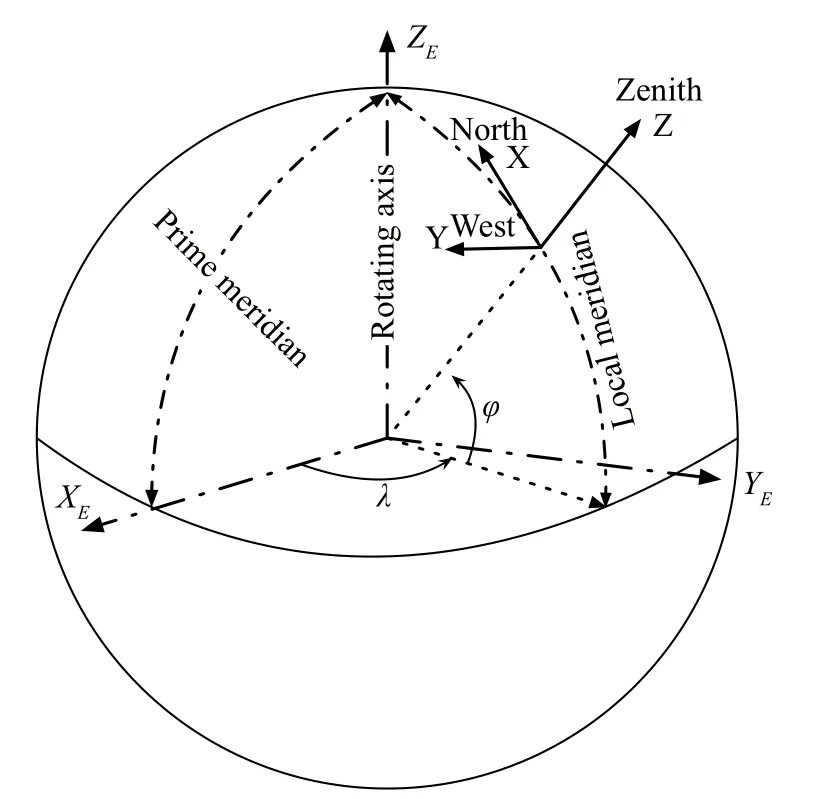
图2 国际地球参考系、地平参考系及其之间关系的示意图Fig.2 The diagram of international terrestrial reference system and horizontal reference system

随着载体的运动,[F]系的位置和姿态是变化的,由惯导系统可得到Ti时刻星下点的地理经纬度(λi,φi)、航向、俯仰和滚动角(ψi,θi,ϕi),据此可得到某T0时刻到T1时刻[F]系的姿态转换矩阵△FG:

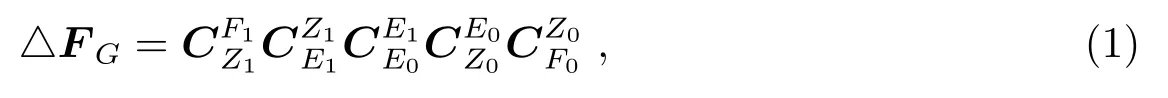
2.3 由天文观测数据计算坐标转换矩阵

在飞机等运载体上安装天文望远镜,使其与运载体固连,且联系参数不随时间变化.由照相天体测量理论可知,利用该机载望远镜进行对天观测可以直接获得所观测天体在望远镜本体坐标系中的方向参数.由于望远镜与运载体固连且其联系参数可事先获知,观测到恒星天体后将可以直接得到该时刻所观测天体在[F]系中的方向参数[8].若在某时刻同时观测角距离跨度比较大的不同方向上的3颗天体,可得到这3颗天体在[F]系中的坐标,天体在[G]系中的坐标可从其星表数据出发经过一套严格的天体测量理论计算得到,联立所观测天体在[G]系和[F]系中的坐标参数,可解算出该时刻[F]系到[G]系的转换矩阵.

设T0时刻3颗天体在[F]系的3维坐标分别为:A=(a1a2a3)T、B=(b1b2b3)T、C=(c1c2c3)T,由星表计算得到的3颗天体在[G]系的坐标分别为:R=(r1r2r3)T、S=(s1s2s3)T、T=(t1t2t3)T.

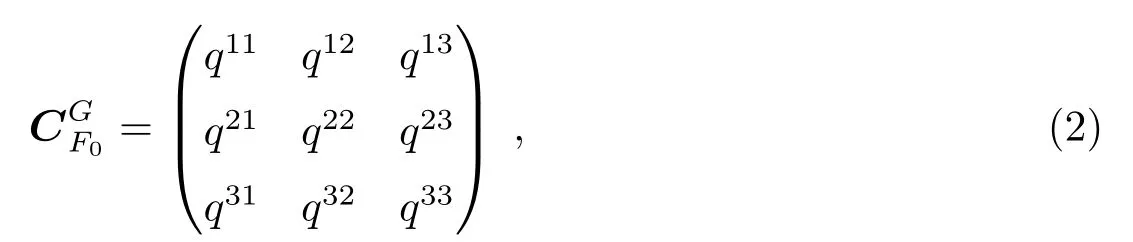
其中qij(i=1,2,3,j=1,2,3)为该矩阵第i行第j列的值.则由

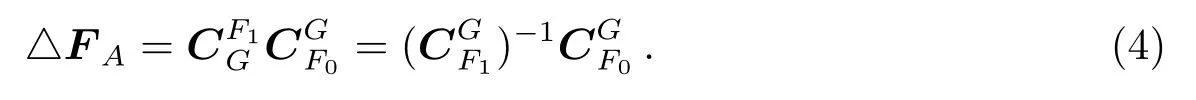
实际操作中,在某一时刻同时观测到3颗角距跨度较大的恒星一般难以实现.这里我们提出了一种新的观测方式用以克服这一困难,即从给定时刻开始在较短时间(如1–2 min)内连续观测3颗天体,将后两次观测量基于天文算法统一归算到第1次观测时刻的[F]系下.下面以第2次观测向第1次归算为例加以说明(第3次向第1次的归算与第2次向第1次归算方法一致).

设在间隔极短的t0、t1、t2时刻分别观测了3颗天体,对于第2次观测时刻(t1时刻) [F]系到第1次拍摄时刻(t0时刻)[F]系的转换,在这极短的时间内,转换过程将对起点和终点的姿态参数误差不敏感,而只与起点和终点的较差量有关,可以认为这3次观测时刻内[F]系的惯导漂移变化平稳,即可认为这短暂时段内惯导系统给出的姿态参数的较差值是准确的.则第2次(t1时刻)向第1次(t0时刻)的[F]系的转换矩阵可利用(1)式得出(此时(1)式中的T0时刻和T1时刻分别表示t0时刻、t1时刻).

2.4 基于坐标转换矩阵差异求解惯导漂移

以天文系统给出的转换矩阵△FA为参考矩阵,联合惯导系统给出的转换矩阵△FG,假设在T0时刻到T1时刻的时间段内惯导系统的坐标系存在绕其3个坐标轴有慢速微小旋转(即漂移),且绕第1、第2和第3轴的旋转量分别为△Y、△X、△θ,则可通过下面的式子解算出惯导系统的漂移量△Y、△X、△θ:

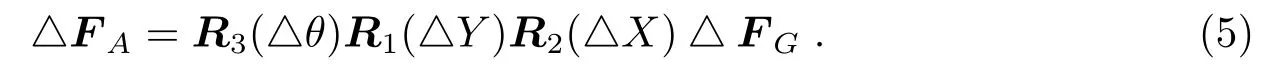
由于偏移量是小量,上式可进一步化简为:

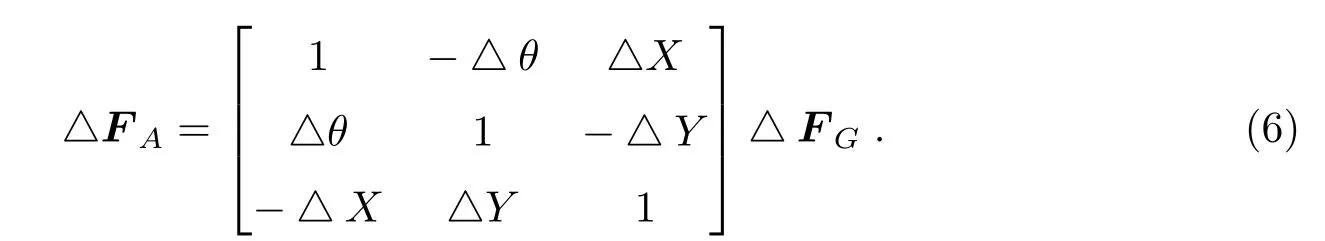
有了惯导系统给出的参数和天文观测的数据,通过以上各式基于最小二乘原理便可解算出给定时间段内惯导系统的漂移量,而偏移量对时间的求导就可给出漂移速率,基于这些参数可对惯导系统进行纠偏改正.

3 模拟软件介绍

基于上述理论和方案编写了相关软件.软件的配置文件中存有CCD相机成像模型参数和望远镜在飞行器上的安装参数.CCD相机成像模型可人为选定,其中1阶模型为6参数,2阶为12参数,3阶为20参数.实际工程应用时,需要基于对密集标准天区标定后再确定具体模型及其参数个数.正常情况下,这些参数一经确定不会变化,如有变化可再次对天标定.望远镜本体坐标系与运载体本体系间的联系参数可以用3个卡尔丹角(Yaw,Pitch,Roll),也可以用对应的转换矩阵的9个元素表示.目前程序配置文件中默认使用3个卡尔丹角.

除了配置文件外,软件还有一个存有观测数据的输入文件,其中存有望远镜拍摄目标天体时的天文和惯导数据信息.数据至少要有两组,每组3个数据点,每个数据点的内容为:望远镜露光开始时刻所观测天体的星表坐标和对应的CCD量度坐标,此时望远镜的轴系指向参数,此时惯导系统给出的运载体的星下点地理经纬度和运载体相对于地平的姿态参数(航向、俯仰和滚动角).软件将基于此数据计算惯导系统在这期间的漂移量.对每一组观测量,要求尽量在较短的时间内收集完成(如1–2 min之内),但对于不同组之间的观测量,则要求适当加长时间跨度(如3–5 min).

软件的输出结果文件中存有惯导系统绕其自身3个坐标轴的漂移量和漂移速率,这里以天文定义的惯性坐标系为基准.软件还输出了运载体坐标系转换到当地地平坐标系的转换矩阵的9个参数.这几个参数可以从望远镜的地平姿态参数直接计算得到,也可以从天文观测数据归算得到,软件给出的是天文数据归算得到的结果.

4 数据模拟和结果分析

依据该方案和软件并考虑试验用的地面样机的相关参数进行了非常接近真实情况的模拟,模拟中所涉及的主要参数有:望远镜焦距f,CCD像素大小p,CCD相机成像采用一阶模型,不同时刻视场中央的指向在地心天球坐标系中的天球坐标;运载体初始姿态角度,望远镜安置角,即望远镜本体的轴系与运载体轴系的关系(默认它们指向一致);惯导系统给出的运载体在不同时刻星下点地固坐标参数、姿态数据(即航向、俯仰和滚动角);地固坐标系X方向的极移,Y方向的极移;地球自转角变化UT1–UTC,UTC跳秒, TAI–UTC.模拟时,对可观测天体做了一定的限制,所观测天体的星等限制在V=−2.0 mag到V=4.0 mag,地平高度限制在30◦到50◦.

首先,假设观测数据没有误差,对单轴漂移进行模拟的情况如下.这里将导航陀螺的理论漂移率设为0.001–0.01 degree·h−1的范围之内,数据点的间隔为0.001 degree·h−1,模拟结果的相对误差大小如图3所示.从图可知,对模拟结果的误差而言,随着漂移率的增大,相对误差逐渐变小.在漂移率为0.01 degree·h−1的情况下(非常接近目前我国惯导可达的最好水平),本方法的相对误差可好于1%,基本可以认为计算结果可靠.

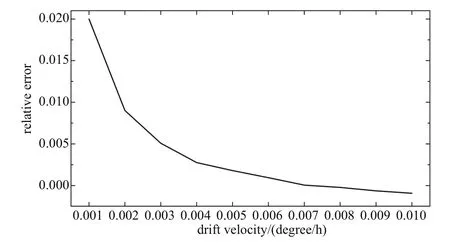
图3 相对误差随漂移率的增大而变小Fig.3 The decrease of relative error with the drift velocity

进而,假设运载体静止不动,其本体系与惯性系重合,天文照相观测时中央指向CCD定位误差为0.1′′,分别模拟没有漂移和单轴有漂移以及3轴均有0.01 degree·h−1漂移率的情况.在1 193 s内,得到的数据如表1–3所示.

表1 理论无漂移时的模拟结果Table 1 The simulation results without drift

表2 第1轴有漂移时的模拟结果Table 2 The simulation results with a drift around the first axis

表3 3轴均有漂移时的模拟结果Table 3 The simulation results with a drift around all the three axes

考虑到软件所使用一些数据和算法的误差,该套方案在可接受的范围(1%)内能够有效地求解惯导的漂移量.

5 结论

本文提出了一种基于天体测量方法解算惯导系统角度漂移的方案,详述了其基本原理和实现过程.该方案对光学望远镜观测恒星的方式和不同时间观测数据联合解算漂移量的处理方法进行了一定的创新.本方案计算精度高、不依赖额外信息,实时性好且操作难度较低.仿真模拟的结果显示,利用本文设计的方案及相关软件能够较好地解算惯导系统的角度漂移量,进而可有效提高惯性导航系统的导航效果.该方法计算漂移过程中忽略了地球公转的影响,以后的工作可考虑加入该项以进一步提高精度.

致谢感谢上海天文台赵铭研究员的帮助,感谢中国兵器工业集团公司第五五九厂对本工作的大力支持并提供相关仪器参数,感谢审稿老师为完善本论文所提出的宝贵修改意见和建议.

[1]秦永元.惯性导航.北京:科学出版社,2005

[2]全伟,刘百奇,宫晓琳,等.北京:国防工业出版社,2011:215-218

[3]徐瑞,朱筱虹,赵金贤.测绘科学,2013,38:40

[4]魏伟,武云云.现代导航,2014,1:62

[5]陈海明,熊智,乔黎,等.传感器与微系统,2008,27:4

[6]谭汉清,刘垒.飞航导弹,2008,5:44

[7]Petit G,Luzum B.IERS Conventions(2010),2010,IERS Technical Note No.36

[8]赵铭.天体测量学导论.北京:中国科学技术出版社,2012

The Principal of a New Method for Estimating the Rotation Drift of Inertial Navigation System with Astrometric Techniques and Its Simulation

QI Zhao-xiang1GUO Su-fen1,2YU Yong1TANG Zheng-hong1

(1 Shanghai Astronomical Observatory,Chinese Academy of Sciences,Shanghai 200030) (2 University of Chinese Academy of Sciences,Beijing 100049)

The precision of Inertial Navigation System(INS)on the air vehicle is strongly a ff ected by the accumulation errors of the rotation drift around its three axes. A new method is proposed in detail for estimating the drift via astrometric techniques. A simulation software is developed according to the algorithm used for this method.It can produce the observational data,estimate unknowns of the drifts of three axes,and also evaluate the result of the proposed method.The feasibility of proposed method is shown with the experiments done with the simulation software.

astrometry,reference systems,methods:observational

P128;

:A

10.15940/j.cnki.0001-5245.2016.03.005

2015-09-22收到原稿,2015-12-03收到修改稿

∗国家自然科学基金项目(11273003,11573054)资助

†kevin@shao.ac.cn