灰色系统模型在UT1–UTC超短期预报中的应用∗
2016-06-27赵丹宁蔡宏兵
雷 雨 赵丹宁 蔡宏兵
(1中国科学院国家授时中心西安710600)
(2中国科学院时间频率基准重点实验室西安710600)
(3中国科学院大学北京100049)
灰色系统模型在UT1–UTC超短期预报中的应用∗
雷 雨1,2,3†赵丹宁1,3蔡宏兵1,2
(1中国科学院国家授时中心西安710600)
(2中国科学院时间频率基准重点实验室西安710600)
(3中国科学院大学北京100049)
依据灰色系统理论和UT1–UTC的变化规律,以较少的观测样本建立了预报UT1–UTC的灰色系统模型,并将其与人工神经网络(arti ficial neural network,ANN)、最小二乘(least squares,LS)与自回归(autoregressive,AR)模型的组合(LS+AR)方法以及地球定向参数预报比较竞赛(Earth Orientation Parameters Prediction Comparison Campaign,EOP PCC)的预报结果进行对比.结果表明:灰色系统模型用于UT1–UTC预报是高效可行的,尤其是在1–10 d跨度的超短期预报中预报效果显著.
天体测量,时间,方法:其他诸多方面
1 引言
地球自转运动表征了地球整体的转动运动状态,可以用地球定向参数(Earth orientation parameter,EOP)来描述,包括岁差、章动、极移和UT1–UTC几个分量. EOP是实现地球参考系与天球参考系相互转换的必需参数,在现代空间导航、深空探测以及天文地球动力学研究等领域都有重要应用.现代空间测地技术如全球卫星导航系统(Global Navigation Satellite System,GNSS)、卫星激光测距(Satellite Laser Ranging, SLR)和甚长干涉基线测量(Very Long Baseline Interferometry,VLBI)等是获取EOP的主要手段,但复杂的资料处理过程使得EOP的获取存在一定的延迟,所以对EOP进行高精度预报是一项非常重要的工作.
在EOP的几个分量中,UT1–UTC是变化最快、最难预报的一个分量,因此,UT1–UTC的高精度预报是EOP预报的难点也是当前的研究热点.目前预报UT1–UTC的方法有多种,如最小二乘外推[1−2]、LS外推和自回归模型的组合[2−5]、人工神经网络[6−8]、高斯过程(Gaussian processes,GP)[9−10]以及小波分解(wavelet decomposition,WD)和自协方差(autocovariance,AC)模型的组合(WD+AC)[11]等.为了比较不同方法的预报效果,维也纳理工大学大地测量与地球物理研究所从2005年10月1日至2008年2月28日组织了全球性的EOP预报比较竞赛,竞赛结果表明,没有一种方法既适合EOP所有分量的预报又适合所有跨度的预报[12].
灰色系统是我国邓聚龙教授于1982年提出的一种研究少数据、贫信息不确定性问题的新方法,它是既含已知信息又含未知信息或非确知信息的系统,已知的信息为“白色”,未知的信息为“黑色”,不充分、不完全的信息为“灰色”[13].灰色系统通过对原始数据实行累加或累减使之成为具有较强规律的新数列,然后对生成的新数列进行建模.它不需要较大的数据量,只要原始序列有4个以上数据就可以建立灰色系统模型,提供了贫信息情况下解决系统问题的新途径.
目前UT1–UTC预报大多是采用国际地球自转与参考系服务(International Earth Rotation and Reference Systems Service,IERS)发布的EOP C04序列作为基础序列,在常规情况下数据量是充足的,但在非常时期一旦IERS暂停其EOP服务,就存在数据量不足的情形,传统LS等模型就不再适用,而灰色模型却为小样本情况下的UT1–UTC预报提供了一种可行方法;另一方面,近年来国内相关单位致力于提供自主的EOP服务,正在建设以数字天顶筒为主要观测设备的EOP自主测量与服务系统,然而受限于光学测量技术的限制,获得的EOP测量数据是不连续的,在这种条件下开展EOP预报服务,必须寻求适合于贫信息情况下的时间序列预报方法,而灰色模型为贫信息情况下的UT1–UTC预报提供了一种可行途径.
由于受众多激发源的影响,UT1–UTC的变化极为复杂,不仅包括年际变化、季节性变化以及几十天的短周期变化,同时还包括不规则的高频变化,从而很难掌握其复杂细致的变化规律,但这符合灰色系统理论的特点.因此,本文尝试将UT1–UTC的变化过程视为灰色系统,将灰色系统模型引入UT1–UTC超短期预报研究中,研究表明:灰色系统模型用于UT1–UTC超短期预报是可行的,且预报精度和预报效率较高.
2 灰色系统模型
在灰色系统理论中,GM(1,1)模型是外推法的一种新的开拓,是最常用的一种灰色系统模型,是由一个仅包含单变量的1阶微分方程构成的模型,适合对本身数据的预报.
设有变量X(0)的原始数据序列:
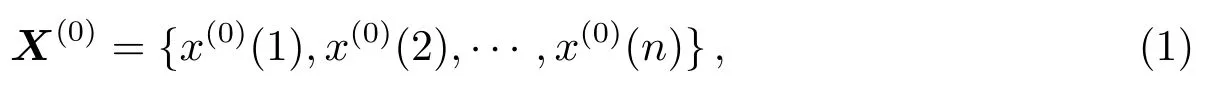
其中,n为原始数据个数,与之对应的时间为t(t=1,2,···,n).对原始序列进行累加生成1阶累加模块X(1)
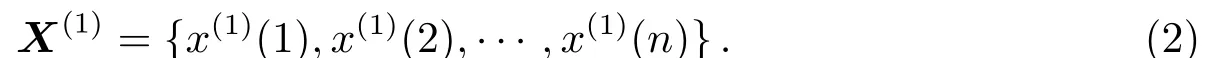
由模块X(1)构成的微分方程为

其中,a为发展系数,b为灰色作用量.根据导数离散化形式,(3)式可以写成矩阵形式:

利用最小二乘原理,可求得参数估值:
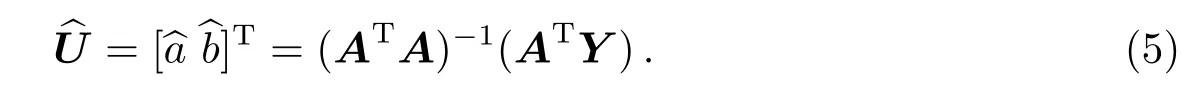
求得参数估值后,可得到微分方程的解:

离散形式为
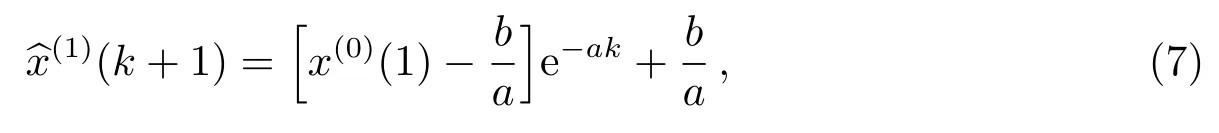
其中,k为参与预报的原始数据个数.
一般形式为
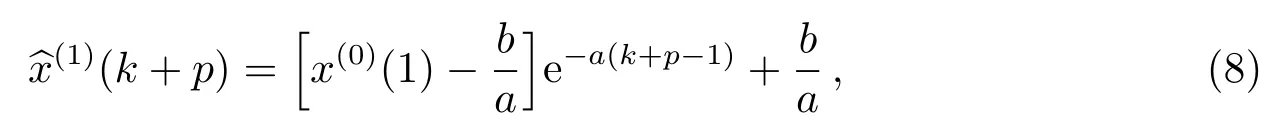
其中,p为预报点数,则预报后的原始观测序列为
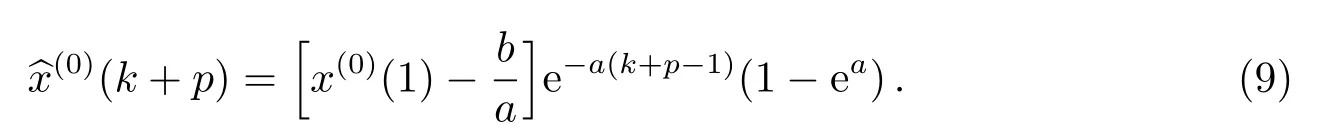
在建模前,必须检查原始数据序列符号是否一致,若不一致,则给每个元素均加上一个常数,使序列的符号一致,然后在此基础上建立GM(1,1)模型并进行预报,最后再从预报值中减去所加常数即可获得所需的预报值.所加常数的取值原则是,符号与原始序列中绝对值最大的数的符号一致,且其绝对值大于原始序列中绝对值最大数的绝对值.
3 实验分析
本文实验数据来自IERS发布的EOP C04序列,数据采样间隔为1 d.在对UT1–UTC建模之前,首先去掉UT1–UTC序列中的闰秒得到UT1–TAI(International Atomic Time,国际原子时)序列,然后根据IERS协议扣除UT1–TAI序列中周期为5 d–18.6 yr的固体地球带谐潮汐项获得UT1R–TAI序列,其中UT1R表示经过固体地球带谐潮修正后的UT1,最后再利用GM(1,1)模型对UT1R–TAI序列建模预报.图1(a)–1(d)分别绘出了1990年1月1日至1997年12月31日期间的UT1–UTC原始序列、UT1–TAI序列、UT1R–TAI序列及其累加序列.
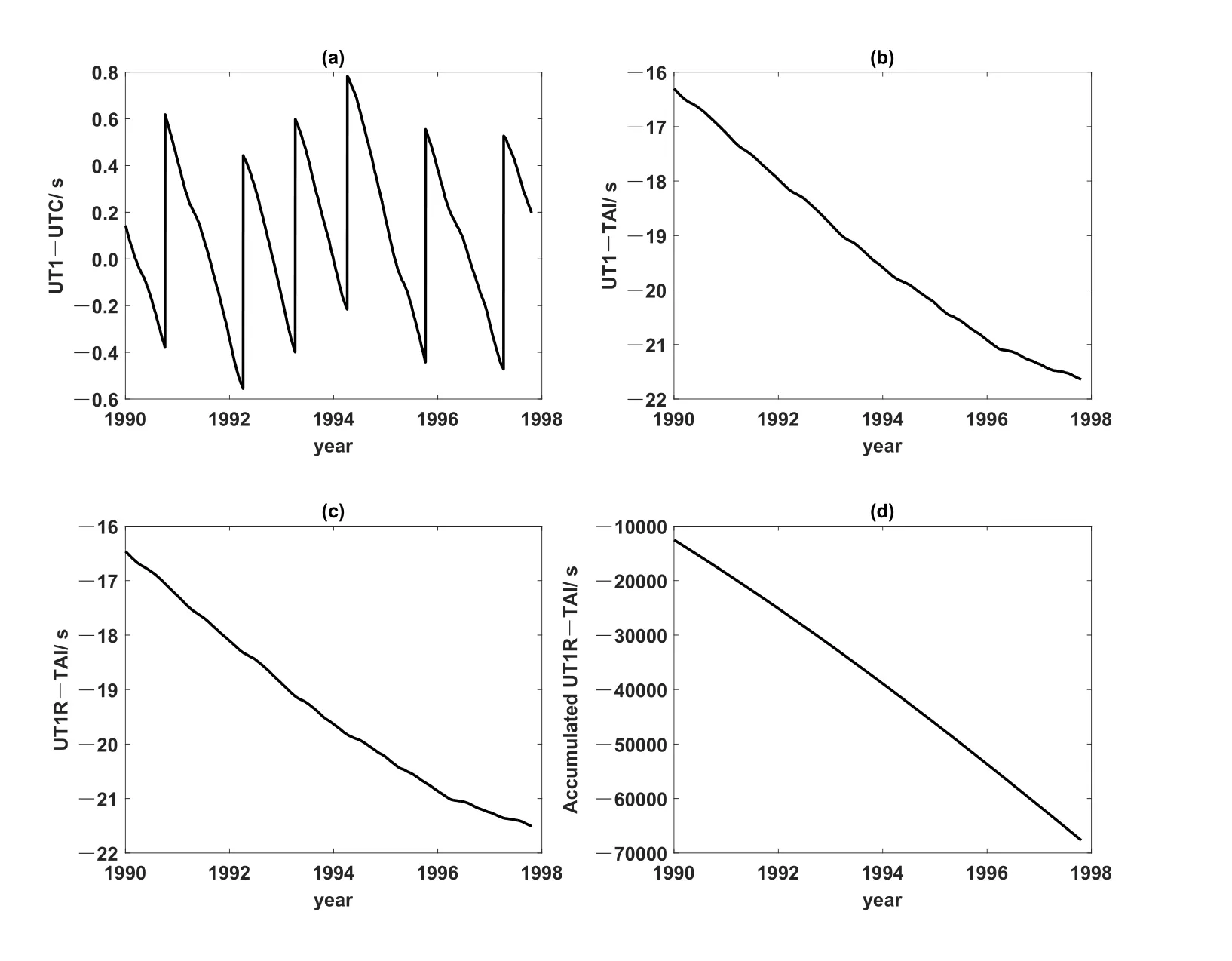
图1 (a)UT1–UTC原始序列;(b)UT1–TAI原始序列;(c)UT1R–TAI原始序列;(d)UT1R–TAI的累加序列Fig.1 (a)The original series of UT1–UTC;(b)the original series of UT1–TAI;(c)the original series of UT1R–TAI;(d)the accumulated series of UT1R–TAI
由图1可以看出,扣除闰秒和潮汐项后的UT1–UTC序列呈不规则变化,其变化规律不明显,但一次累加后的新序列比较光滑,比较符合指数变化规律,所以从理论上讲,应用GM(1,1)模型对UT1–UTC进行预报是完全可行的.我们首先分析了基础序列长度对GM(1,1)模型预报效果的影响,结果发现基础序列长度越短,预报效果越好,限于篇幅,图2仅绘出了基础序列长度为4、8、12和16时GM(1,1)模型的预报均方根误差(root mean square error,RMSE),其计算公式为
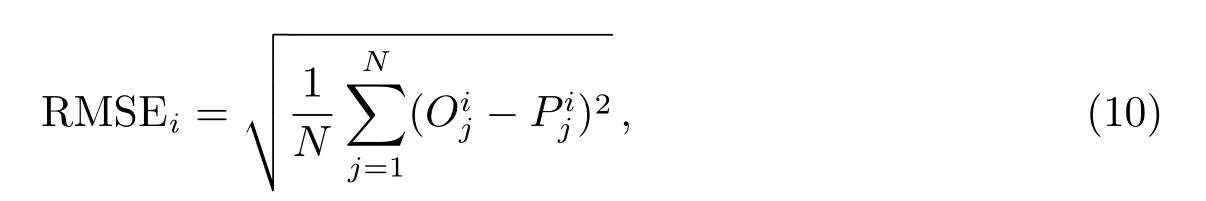
图2中,圆形实线表示基础序列长度n=4时,GM(1,1)模型的预报RMSE,三角形实线表示基础序列长度n=8时,GM(1,1)模型的预报RMSE,圆形虚线表示基础序列长度n=12时,GM(1,1)模型的预报RMSE,三角形虚线表示基础序列长度n=16时,GM(1,1)模型的预报RMSE.对于每一种建模方案,我们均进行了700期的1–30 d跨度的预报(N=700),预报时间段为1998年1月1日至1999年12月31日,每隔1 d预报1次.从图2可以看到,基础数据序列长度为4时预报效果最佳,所以在接下来的预报实验中我们仅采用4个历元的数据建立GM(1,1)模型.
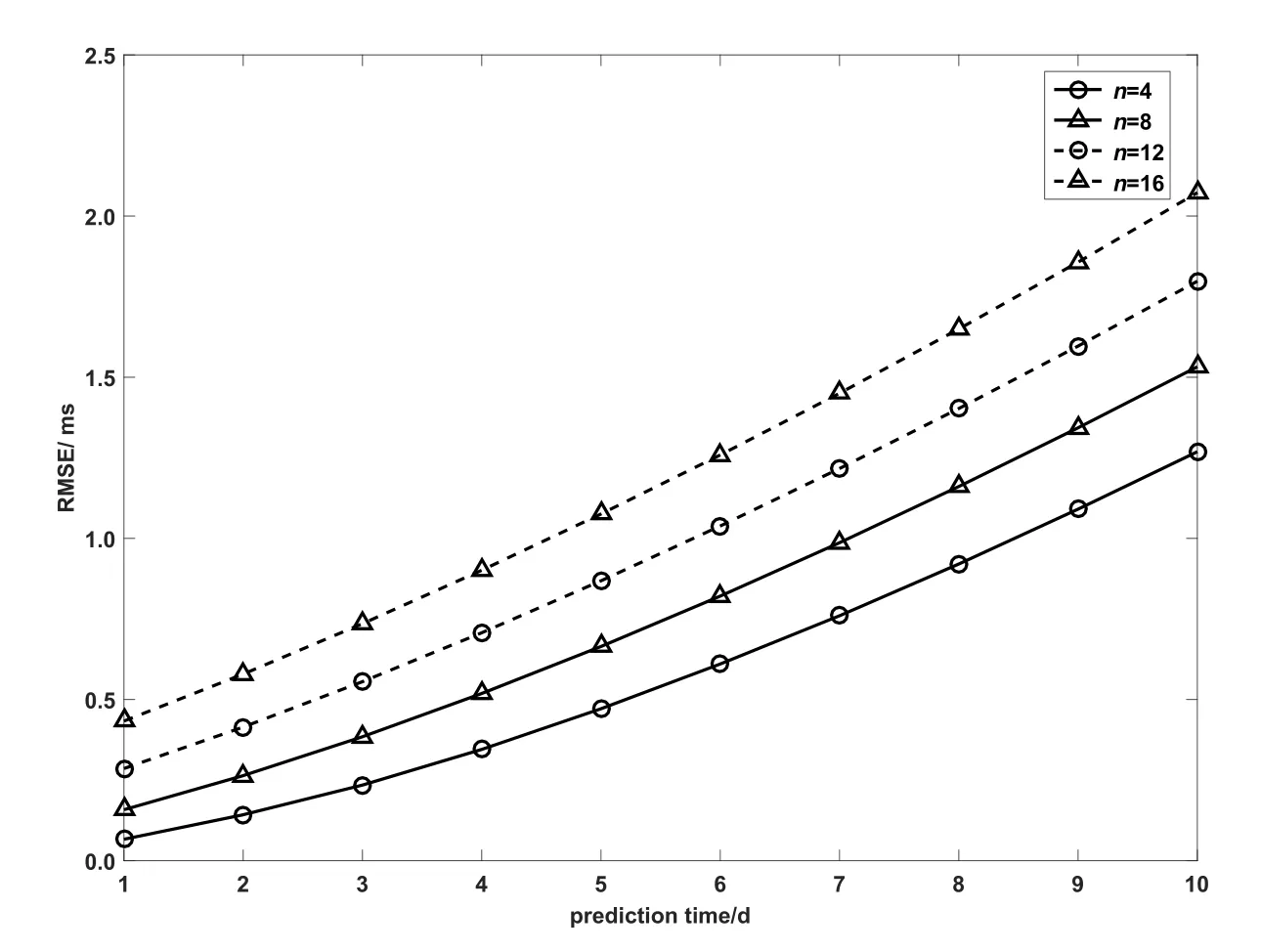
图2 UT1-UTC不同基础序列长度预报精度Fig.2 The comparison of the prediction accuracies for di ff erent data intervals
由于ANN和LS+AR模型是预报UT1–UTC精度较高的两种方法,所以为了验证GM(1,1)模型的预报效果,我们将GM(1,1)模型的预报结果分别与Schuh等[6]所使用的ANN模型与Xu和Zhou[3]所使用的LS+AR模型的预报结果进行比较,RMSE比较结果见图3–4和表1–2.图3–4中,圆形实线表示GM(1,1)模型的预报结果,三角形实线和方形实线分别表示Schuh等[6]与Xu和Zhou[3]的预报结果.由表1–2可以看出,GM(1,1)模型用于UT1–UTC预报是比较成功的,随着预报跨度的增大,预报精度有所降低.从表1和图3的对比中可以看到,对于1–6 d的超短期预报,GM(1,1)模型的预报精度与Schuh等[6]的预报精度大致相当,从第7 d开始,GM(1,1)模型的预报精度低于Schuh等[6]的预报精度并逐渐拉开差距,特别是从第10天开始,前者的预报精度明显低于后者.从表2和图4可以看到,对于提前1 d预报,GM(1,1)模型的预报精度明显优于LS+AR模型,对于10 d跨度预报,两者的预报精度相当,而对于20 d和30 d跨度预报,前者的预报精度则不及后者.
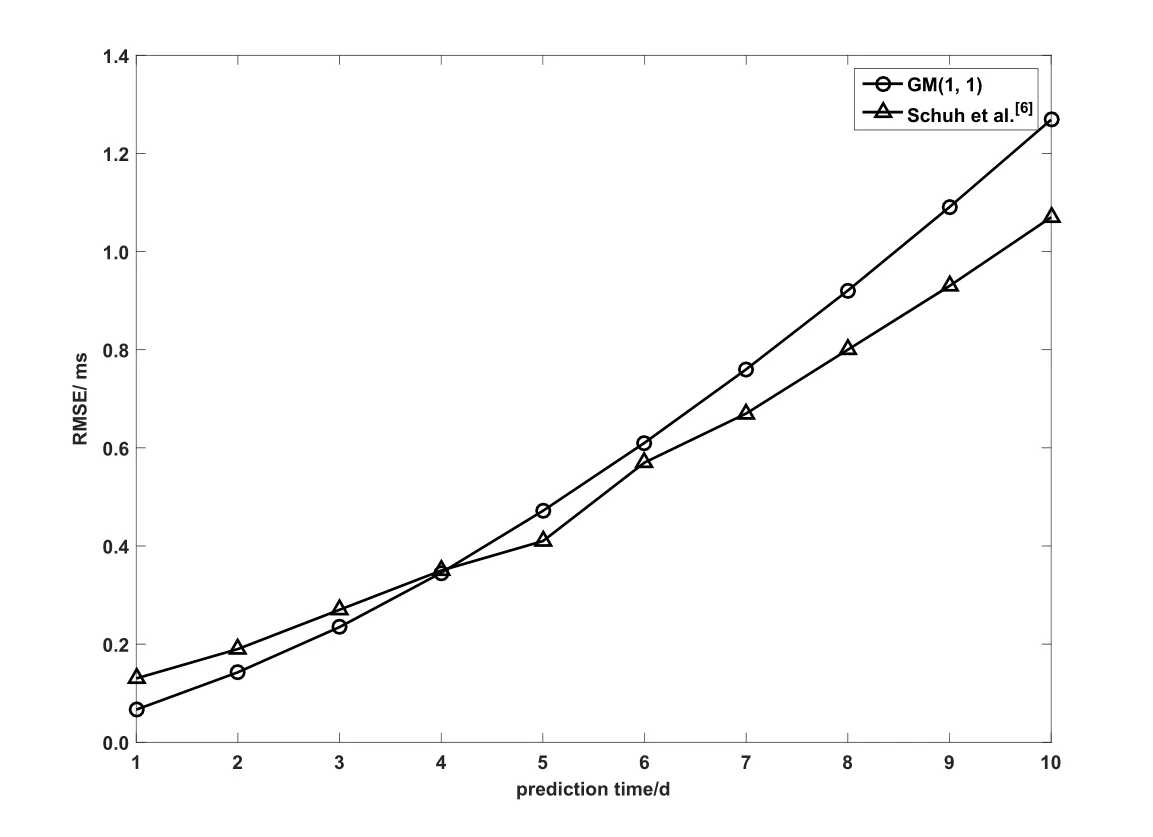
图3 GM(1,1)模型预报精度与Schuh等[6]预报精度比较Fig.3 The comparison of the prediction accuracies of GM(1,1)and Schuh et al.[6]

图4 GM(1,1)模型预报精度与Xu和Zhou[3]预报精度比较Fig.4 The comparison of the prediction accuracies of GM(1,1)and Xu and Zhou[3]
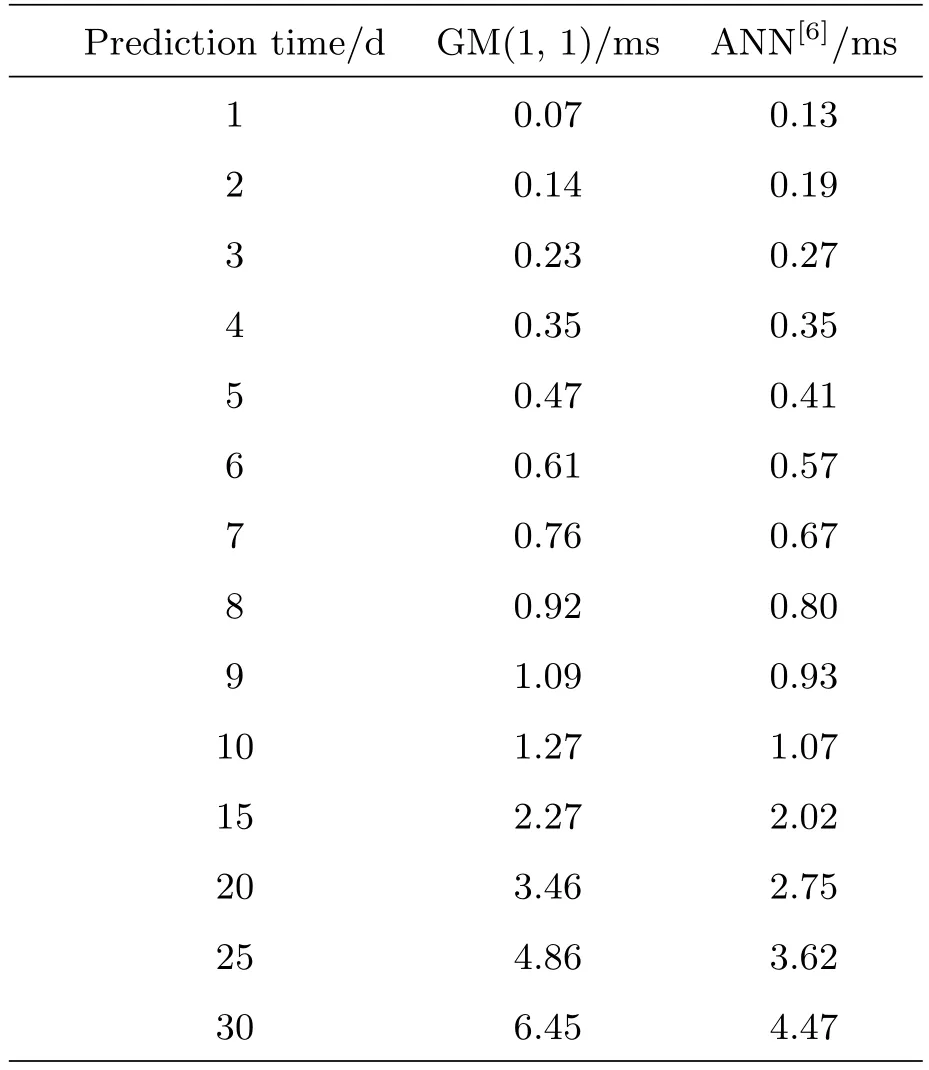
表1 GM(1,1)模型预报精度与ANN预报精度(Schuh等[6]的预报结果)的比较Table 1 The comparison of the prediction accuracies of GM(1,1)and ANN(Schuh et al.[6])
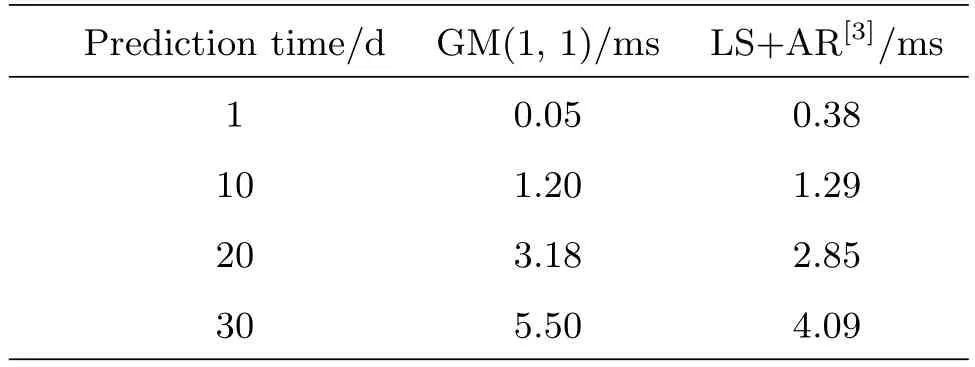
表2 GM(1,1)模型预报精度与LS+AR预报精度(Xu和Zhou[3]的预报结果)的比较Table 2 The comparison of the prediction accuracies of GM(1,1)and LS+AR(Xu and Zhou[3])
为了进一步探讨GM(1,1)模型用于UT1–UTC预报的性能,本文也预报了2005年10月1日至2008年2月28日(与EOP PCC时间段相同)不同跨度的UT1–UTC值,统计了预报结果的平均绝对误差(mean absolute error,MAE),并同EOP PCC结果进行了对比,对比结果见图5–6,其中MAE的计算公式为
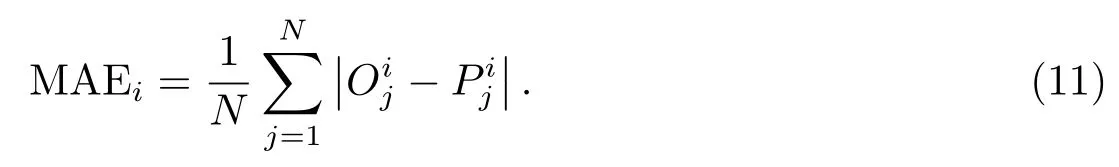
图5–6中不同形状曲线分别为参与EOP PCC不同小组所获得的预报结果,其中3位数字代表各小组编号,EOP PCC中UT1–UTC预报精度较高的两个小组分别是Gross小组和Gambis小组,这两个小组均联合大气角动量数据进行UT1–UTC预报.图5–6中圆形点线、方形点线和菱形点线(编号091–093)表示Zotov小组的预报结果,三角形实线(编号071)表示EOP产品中心的预报结果,三角形虚线(编号031)表示Gross小组的预报结果,圆形虚线表示本文预报结果.图5中五角星实线、方形实线、菱形实线和圆形实线(编号072–075)表示Gambis小组的预报结果.图6中五角星实线(编号053)表示Kosek小组的预报结果.
从图5的比较可以看到,对于1–5 d的超短期预报,GM(1,1)模型的预报精度仅次于排在第1位Gross小组的精度,与排在第2位的Gambis小组的精度相当,从第6天开始, GM(1,1)模型的预报精度低于Gross小组、Gambis小组的精度并逐渐拉开差距,但仍优于其他小组的预报精度或与之相当.从图6可以看出,对于1–30 d的短期预报,当预报跨度在10 d以内时,除Gross小组的预报精度超过GM(1,1)模型外,其他小组的预报精度与GM(1,1)模型精度大致相当,当预报跨度超过10 d时,GM(1,1)模型的预报精度则开始变差,不如大部分小组的预报精度.
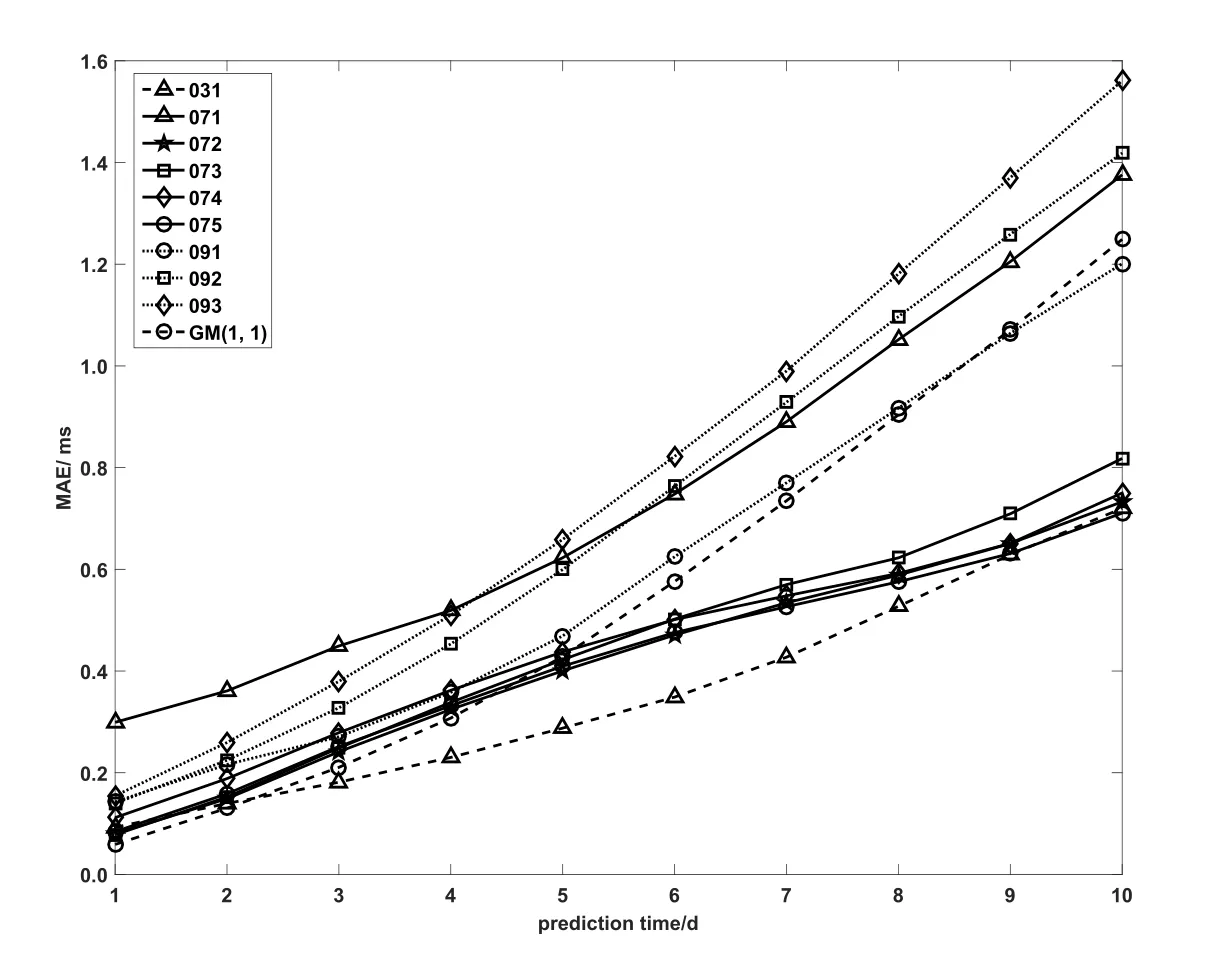
图5 GM(1,1)模型超短期(1–10 d)预报精度与EOP PCC结果的对比Fig.5The comparison of the prediction accuracies of GM(1,1)and EOP PCC for the ultra short-term (1–10 d)
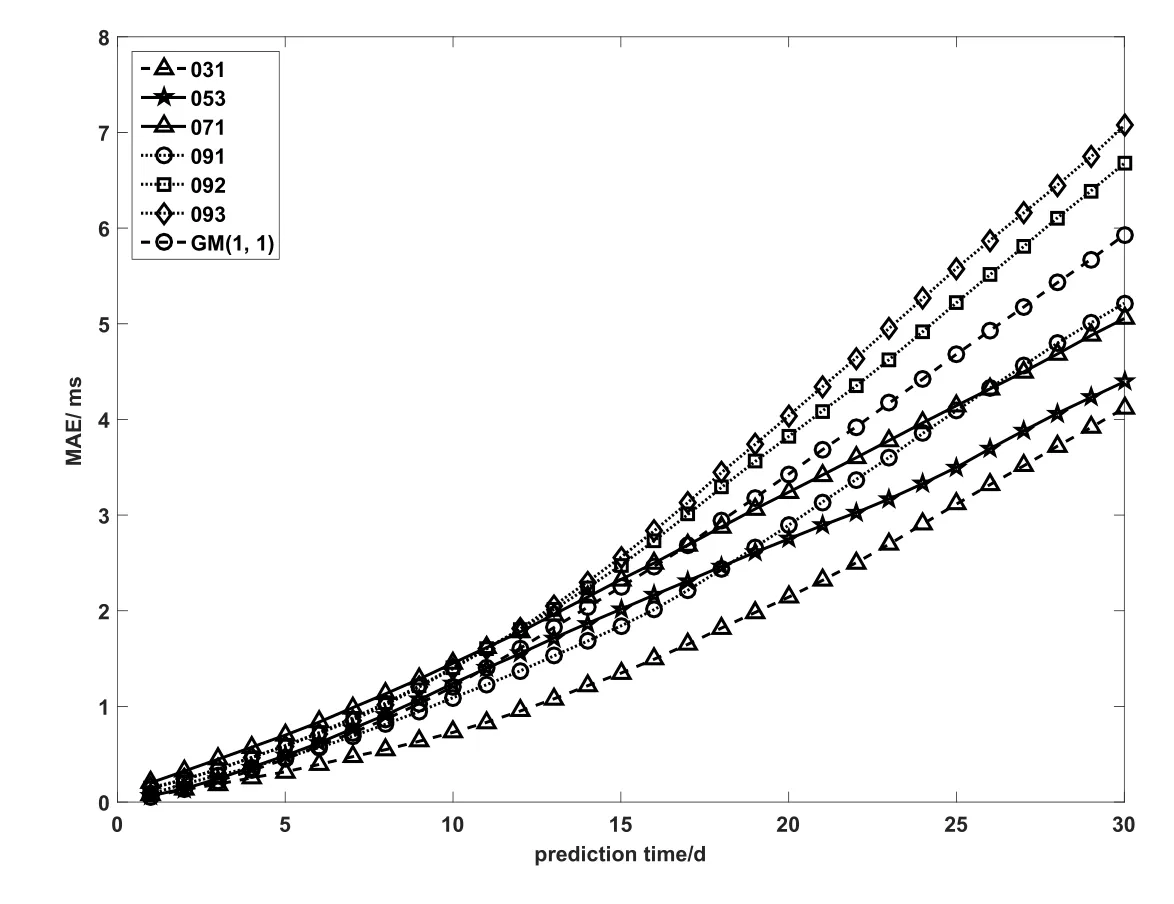
图6 GM(1,1)模型短期(1–30 d)预报精度与EOP PCC结果的对比Fig.6 The comparison of the prediction accuracies of GM(1,1)and EOP PCC for the short-term (1–30 d)
4 总结与展望
本文通过实例验证了GM(1,1)模型用于UT1–UTC预报的可行性和有效性.通过与Schuh等[6]所使用的ANN模型以及与Xu和Zhou[3]所使用的LS+AR模型的预报结果的比较可以发现,虽然在20–30 d跨度的预报中GM(1,1)模型的预报效果远不及ANN和LS+AR模型,但对于1–10 d跨度预报GM(1,1)模型的预报精度却与之相当或稍逊.通过与EOP PCC预报结果的进一步比较,我们同样发现,GM(1,1)模型在1–10 d超短期跨度预报中效果良好,但当预报跨度超过10 d时效果不甚理想.上述分析表明, UT1–UTC累加序列的短期变化比较符合指数变化规律,但长期变化与指数变化规律不符,所以利用GM(1,1)模型来描述UT1–UTC的短期变化特性是比较合适的.
算例表明,GM(1,1)模型的预报精度并非最优,但与其他方法相比具有可比性,尤其是在1–10 d的超短期预报中效果显著,这为UT1–UTC超短期预报提供了一种备选方法.此外,对比现有的UT1–UTC预报方法,GM(1,1)模型有2个优点:一是它仅仅使用已知的少数几个历元的数据便可以建模,减少了要使用的数据量,为小样本情况下的UT1–UTC预报提供了一种有效途径,这对于恢复我国自主的UT1–UTC服务能力有着重要的现实意义;二是GM(1,1)模型简单、易于实现,无需复杂的调整参数就能获得满意的预报效果,极大提高了建模效率,这对于UT1–UTC的实时快速预报有着重要的现实意义.由于UT1–UTC与大气角动量轴向分量有着密切的关系[1−2],下一步的研究我们将会联合大气角动量轴向分量和UT1–UTC序列建立多变量灰色系统模型进行UT1–UTC预报.
[1]Guo J Y,Li Y B,Dai C L,et al.JGeo,2013,70:36
[2]Niedzielski T,Kosek W.JGeod,2008,82:83
[3]Xu X Q,Zhou Y H.AdSpR,2015,56:2248
[4]Sun Z Z,Xu T H.Geodesy&Geodynamics,2012,3:57
[5]许雪晴,周永宏.飞行器测控学报,2010,29:70
[6]Schuh H,Ulrich M,Egger D,et al.JGeod,2002,76:247
[7]Liao D C,Wang Q J,Zhou Y H,et al.JGeo,2012,62:87
[8]Lei Y,Zhao D N,Cai H B.Geodesy&Geodynamics,2015,6:151
[9]雷雨,赵丹宁,高玉平,等.天文学报,2015,56:53
[10]Lei Y,Zhao D N,Gao Y P,et al.ChA&A,2015,39:368
[11]Kosek W,Kalarus M,Johnson T J,et al.ArtSa,2005,40:119
[12]Kalarus M,Schuh H,Kosek W,et al.JGeod,2010,84:587
[13]邓聚龙.灰理论基础.武汉:华中科技大学出版社,2002
An Application in the Ultra Short-term Prediction of UT1–UTC Based on Grey System Model
LEI Yu1,2,3ZHAO Dan-ning1,3CAI Hong-bing1,2
(1 National Time Service Center,Chinese Academy of Sciences,Xi’an 710600)
(2 Key Laboratory for Time and Frequency Primary Standards,Chinese Academy of Sciences,Xi’an
710600)
(3 University of Chinese Academy of Sciences,Beijing 100049)
This work presents an application of the grey system model in the prediction of UT1–UTC.The short-term prediction of UT1–UTC is studied up to 30 days by means of the grey system model.The EOP(Earth orientation parameter)C04 time series with daily values from the International Earth Rotation and Reference Systems Service(IERS)serve as the data base.The results of the prediction are analyzed and compared with those obtained by the arti ficial neural network(ANN),the combination of least squares(LS)and autoregressive(AR)model(LS+AR),and the Earth Orientation Parameters Prediction Comparison Campaign(EOP PCC).The accuracies of the ultra short-term(1–10 d)prediction are comparable to those obtained by the other prediction methods.The presented method is easy to use.
astrometry,time,methods:miscellaneous
P127;
:A
10.15940/j.cnki.0001-5245.2016.03.006
2015-09-28收到原稿,2015-12-02收到修改稿
∗国家自然科学基金项目(11503031)资助
†leiyu@ntsc.ac.cn
