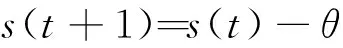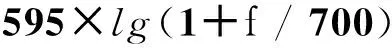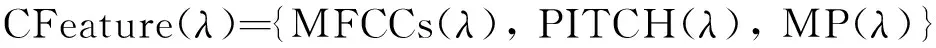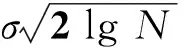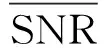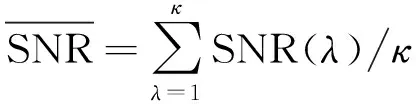一种混合优化的匹配追踪生态声音识别方法
2016-06-23李碧玉
李碧玉, 李 应
(福州大学数学与计算机科学学院,福建 福州 350116)
一种混合优化的匹配追踪生态声音识别方法
李碧玉, 李 应
(福州大学数学与计算机科学学院,福建 福州350116)
摘要:针对生态自然环境中噪声对声音识别产生干扰的问题,提出利用混合优化的匹配追踪(MP)进行生态声音识别的方法. 首先,使用萤火虫算法(GSO)和粒子群算法(PSO)对匹配追踪算法进行混合优化,加快匹配追踪有限次稀疏分解的速度并重构声音信号,保留高相关成分,滤除低相关噪声; 其次,根据所选最优原子的时频信息结合MFCCs提取复合抗噪特征; 最后,结合支持向量机(SVM)对40种生态声音在不同背景噪声与信噪比的情境下进行分类与识别. 实验表明,优化后的匹配追踪算法去噪性能优于谱减法和小波去噪法. 与常用的MFCCs方法相比,本方法对生态声音在不同信噪比下的识别性能有不同程度的改善, 并且具有较好抗噪性.
关键词:生态声音识别; 匹配追踪; 信号重构; 萤火虫优化算法; 粒子群优化算法
0引言
生态环境中有着丰富的音频信息,通过对不同的音频信息进行收集、 分析, 可以为物种勘察和物种入侵检测等研究提供科学有效的数据支持[1]. 文[2]提出频域特征多级平均谱(multi-stage average spectrum, MSAS),结合音节长度对18种蛙类声音进行两次识别分类; 文[3]利用高斯混合模型(GMM)对时频谱形状特征进行建模,利用角度径向变换实现对连续型鸟叫的分类识别. 文[4-5]提取基音、 共振峰和短时能量作为特征集,结合支持向量机(SVM)对19种动物的声音进行识别.
实际生态环境中存在大量的非平稳噪声,对声音信号产生不同程度的干扰,噪声环境下的生态声音识别具有重要的实际意义. 常见去噪方法有维纳(Weiner)滤波、 卡尔曼(Kalman)滤波、 带通滤波、 小波去噪[6]、 谱减法[7]等. 这些去噪算法依赖信号或噪声信号的统计特性作为先验知识,应用范围较为有限. 基于匹配追踪(matching pursuit,MP)的去噪方法利用声音信号稀疏特性,将信号分解重构进行自适应表示,无需先验获得待检测信号和噪声的统计特性,更适用于不同场景的多种信号[8]. 文[9]利用MP与Gabor小波提取显著的音频信号特征,实现机器人试听系统对噪声环境下不同音效的识别. 文[10]通过分析信号子带能量构造信号相关原子字典,利用匹配追踪算法得到稀疏矢量并计算加权特征,用于对14类环境声音进行分类. 然而,计算复杂度高一直是匹配追踪算法在实际应用中存在的最大瓶颈,也是使用该算法亟需解决的关键问题. 匹配追踪算法搜索自适应原子是一个典型的最优化问题,萤火虫群优化算法(glowworm swarm optimization,GSO)[11]和粒子群算法(particle swarm optimization,PSO)[12]都是仿生智能随机优化算法,该类算法利用小规模的种群在大空间进行搜索,能够快速逼近极值域,具备通用性和效率高的特点,可以有效提高全局搜索效率. 尽管使用GSO算法可以快速逼近最优原子的位置,但算法在搜索过程中容易陷入局部最优而影响最终结果. 本研究利用GSO和PSO的混合优化算法来搜索最优原子,在保证求解精度的前提下,提高搜索效率,快速实现声音信号的稀疏分解与重构. 对重构声音信号提取复合特征,最后使用SVM进行识别与分类. 具体过程如图1.

图1 基于混合优化匹配追踪算法的生态声音分类流程图Fig.1 Overview of ecological sounds classification based on hybrid optimized MP approach
1基于GSO+PSO搜索策略的匹配追踪稀疏分解
1.1匹配追踪信号分解
假设待分解信号f,长度N. 稀疏分解前,首先构造过完备原子字典D=(gγ)γ∈Γ,选取的时频原子gγ是Gabor原子.
(1)
式(1)由一个经调制的高斯窗函数g(t)=e-πr2构成,参数组γ=(s, u, v, w)定义Gabor原子,平移因子u定义原子gγ的中心位置,伸缩因子s,频率因子v和相位因子w定义波形,其离散化时频参数为:
(2)
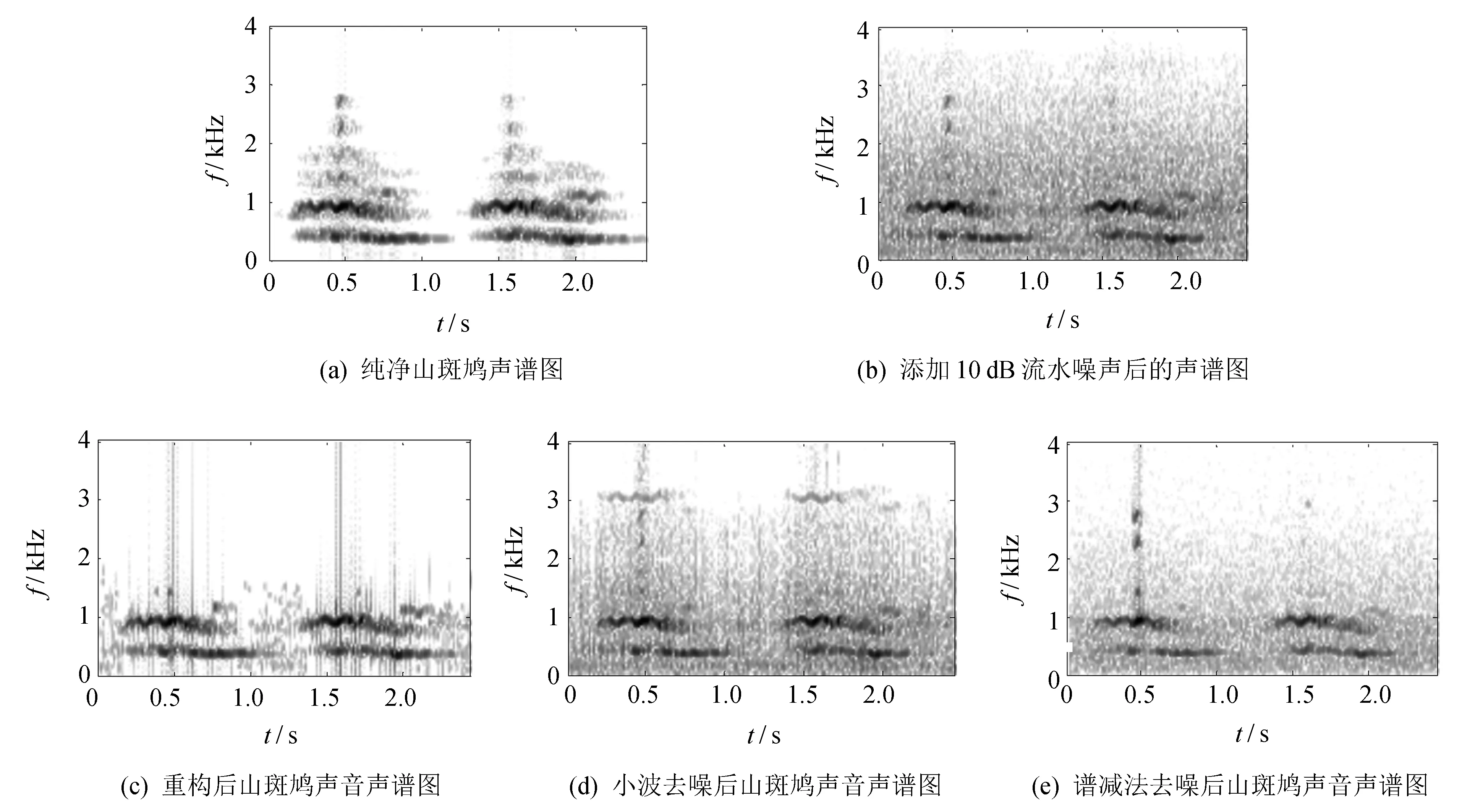
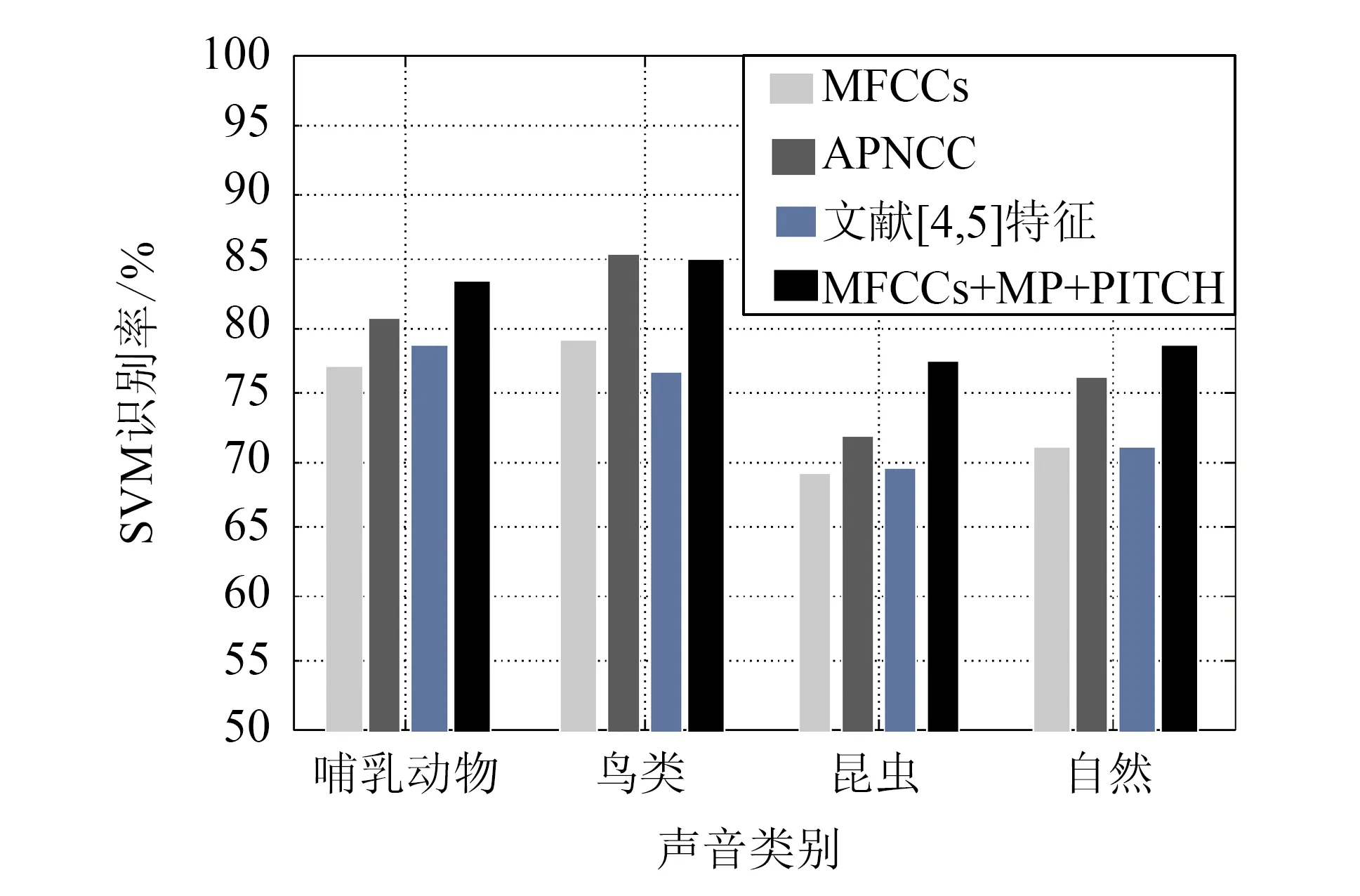
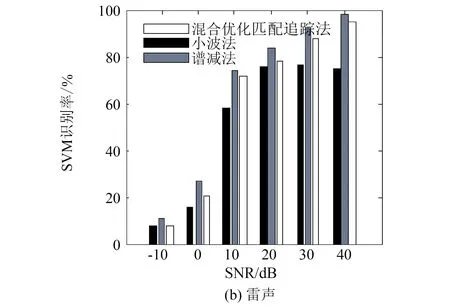
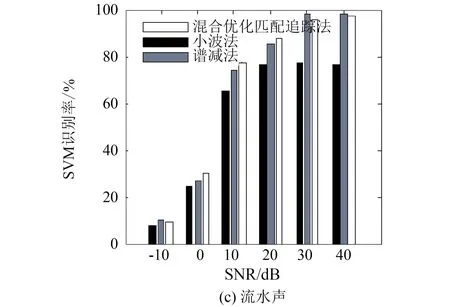
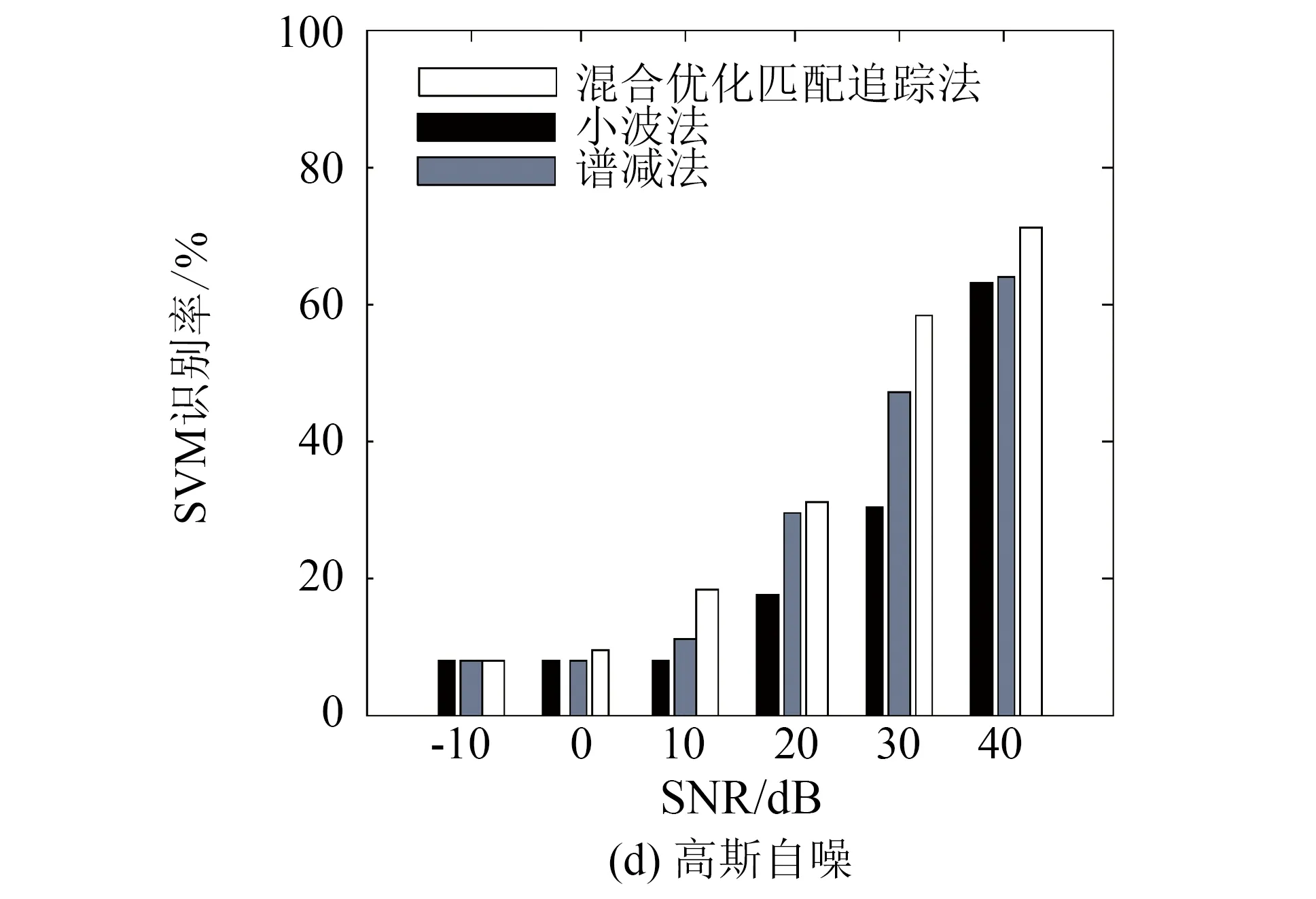
其中: 0 算法具体流程如下: 步骤1初始化信号残差R0=f,迭代次数k=1,最大迭代次数kmax. 步骤2从过完备原子字典D中选出第k次迭代与信号残差最相关的原子gγk. (3) 步骤3将: (4) 进行归一化得到uk,通过将残差投影到uk上得到新的残差: Rk=Rk-1-〈Rk-1, uk〉uk. (5) 若不成立, 且k 1.2GSO+PSO最优原子搜索策略 利用GSO优化搜索最优原子,通过萤火虫的移动和聚集快速得到一个能取得最大荧光素的位置,即最优原子,但GSO容易陷入局部最优影响结果. 为了克服该缺陷,引入精度高的PSO算法对萤火虫优化结果进行进一步的优化,具体步骤如下: 步骤1初始化萤火虫种群规模n,荧光素li,决策域半径r0,最大迭代次数tmax并随机生成萤火虫. 步骤2根据: (6) (7) 计算萤火虫 i 在第 t 次迭代的所处位置xi(t)的目标值 f [xi(t)],并根据: (8) 转化为荧光素值li(t). 其中: ρ∈(0, 1)为荧光素消失率; η∈(0, 1)为荧光素更新率,文中分别取为0.4和0.6. (9) 其中:rs为萤火虫决策域的最大值. 步骤4选取邻域集Ni(t)内荧光素最高的个体j作为移动对象进行移动,并根据: (10) 更新位置xi(t). 其中:s为移动步长,固定步长不利于空间搜索,步长太大,可能导致跳过最优解而降低求解精度,步长太小,则又降低搜索速度. 选取递减式步长作为移动步长. 第t+1次迭代的步长变化式为: (11) 其中:θ为步长调整因子. 步骤5根据 (12) 步骤 6若达到GSO最大迭代次数tmax,保存搜索结果,否则返回步骤 2. 步骤 7在GSO搜索结果中搜索目标值最大的前y只萤火虫. 若y只萤火虫参数标准差小于设定的阈值,直接输出最优原子,否则分别对y只萤火虫进行PSO搜索初始化. 取y=3,设定粒子群规模N、 搜索迭代次数tmax,确定粒子搜索范围[xmin, xmax]、 速度范围[vmin, vmax],在搜索范围内随机生成粒子并设置粒子初始位置和速度,计算每个粒子目标值f [xi(0)]. 每个粒子位置初始值为局部最优解pbest(i),目标函数值最大的pbest(i)为全局最优解gbest. 步骤8根据: (13) (14) 更新粒子速度和位置. 其中: a为收敛因子,值越大则收敛速度越快,取固定值0.729; c1和c2为学习因子,取c1=c2=2; rand为[0, 1]内的随机数; w为惯性权重因子,值越大则粒子速度越大,采用线性递减方式决定w取值,变化如下: (15) 其中:wmax为w的最大值,取值为0.95;wmin为w的最小值,取值为0.4. 步骤9重新计算粒子的目标函数值f [xi(t)],若优于当前pbest(i)则用新位置替换pbest(i),若优于当前gbest则用新位置替换gbest. 若t 步骤10比较y只萤火虫原时频参数组与进行PSO搜索后各自的gbest对应时频参数的目标函数值,输出最优原子时频参数组. 2抗噪复合特征的提取 利用MP对生态声音去噪是利用信号稀疏性的特征,将待提取的有用信息作为稀疏成分,而将噪声作为去除稀疏成分后的残差成分. 噪声具有一定随机性,由于字典中不包含随机原子,故其相关性较低. 根据压缩感知理论,对带噪信号进行低维投影,当观测维数足够包含有用信息时,噪声不具有稀疏性. 残差部分的噪声成分在重构时难以恢复,进而实现去噪目的. 匹配追踪算法分解信号得到的Gabor原子由一个调制的高斯窗函数构成,其局部特性保证了原子时频参数能够较好地刻画信号的非平稳时变特性. 利用匹配追踪算法分解每一帧声音信号,可获得表示该帧信号的支撑集前L个原子时频参数组中伸缩因子s和频率因子v的均值和标准差,构成4维MP特征: (16) 其中:l为信号的帧索引;i表示该帧信号的原子索引;L为原子数. 对于带噪声音信号,随着支撑集原子数目增加,重构精度将不断提升,拥有稀疏特性且高相关的声音信号主体逐渐成型,后期重构时,低相关噪声的重构比例也会提升. 在保证重构精度的前提下,经过实验确定稀疏分解的前10个原子进行重构效果为佳. 因不同声音和噪声的稀疏度并不相同,固定的稀疏度对所有声音进行重构存在一定弊端,且特征维数偏少,单独使用MP时频特征的识别效果并不理想. Mel频率倒谱参数(MFCCs)经常应用于语音信号处理,考虑了人耳的听觉特征,将线性频谱映射到基于听觉感知的Mel非线性频谱中再转换到倒谱上. Mel频率尺度与普通频率的对应转换关系为: (17) 式中:f表示普通频率,由于不同种类的动物叫声在Mel频域上也有着不同的特性,故可将其应用于生态声音识别技术中. 但MFCCs极易为外来噪声所破坏,而生态环境中随机噪声是非常普遍的,本研究采用MP时频特征与MFCCs相结合加上一维PITCH特征组成复合抗噪特征共同刻画生态声音. 抗噪复合特征的获取步骤如下: 步骤1对声音信号进行预处理、 分帧,利用Hamming窗进行信号加窗,帧长取32 ms(256个样本点),帧移取16 ms(128个样本点). 步骤2使用混合优化的匹配追踪算法对每帧声音信号进行重构,提取4维MP特征; 步骤3利用快速傅里叶变换(FFT)将重构后的时域信号转换成信号功率谱; 步骤4采用24阶Mel三角带通滤波器组对信号功率谱进行滤波,对每个滤波器的输出求取对数能量得到24个能量对数; 步骤5对所得能量对数其进行离散余弦变换(DCT),将信号映射到低维空间,得到12维MFCCs静态特征; 步骤6采用循环平均幅度差函数(CAMDF)法获得每帧对应的1维PITCH特征; 步骤7将12维的MFCCs特征、 1维PITCH特征与4维MP特征结合,构成抗噪复合特征: (18) 3实验 3.1实验参数配置 实验所用声音样本集来自录音笔实地所录以及Freesound[13]声音数据库,分为陆地动物叫声、 鸟叫声、 昆虫叫声、 自然声音4大类,共40种声音,具体如表1所示. 每种声音均分割为30段时长为2 s的声音段,共1 200个有效纯净声音段. 每一类选取10段纯净声音作为训练数据,剩余20段混合不同背景噪声组成多组测试数据. 所有声音样本采样频率为8 kHz,采样精度为16位. 表1 生态声音样本集 为了验证本方法对生态声音识别的有效性,并与目前已有的生态声音识别方法做比较,设计以下4组对比实验,以均方误差值MSE和正确识别率为衡量信号重构性能的评估标准,MSE可由下式计算得到. (19) 其中:N为信号长度;n为采样点索引值;f′(n)为重构后的信号;f(n)为原始信号. 实验设置具体如下: 1) 对比传统和现有的匹配追踪优化算法,验证基于GSO+PSO算法混合优化的匹配追踪算法能够在保证重构精度的前提下减小计算复杂度; 2) 与现有经典的去噪算法对比,验证匹配追踪稀疏分解对生态声音去噪的性能及其优越性; 3) 与现有生态声音识别算法对比,验证所选取特征适用于刻画生态声音; 4) 选取真实环境下采集的大自然声音作为背景噪声加入实验,验证本方法在生态场景下对声音的识别能力. 3.2实验结果与分析 3.2.1匹配追踪信号快速分解有效性检验 对不同匹配追踪分解方法进行对比,搜索最优原子的策略分别为标准的全局搜索,单纯基于GSO优化搜索和基于遗传算法(GA)[14]优化搜索. 经过实验确定GSO+PSO混合优化算法中萤火虫种群大小为20,最大迭代次数30, 粒子群种群大小10,最大迭代次数30. 单纯基于GSO的优化算法中萤火虫种群大小为30,最大迭代次数50. 文[14]中遗传算法种群大小为31,最大迭代次数为50次. 选取Freesound声音数据库中的纯净山斑鸠声音用于有效性检验,对单帧长度为256的山斑鸠声音信号进行分解重构10次的计算量如表2所示. 表2 匹配追踪稀疏分解计算量 从表中可以看出,GSO+PSO算法大大减少了匹配追踪重构的计算量,相比单纯的GSO搜索在内积计算次数相近的情况下,其重构质量要优于单纯GSO的重构质量. 文[14]的基于遗传算法的搜索策略由于选择算子时需要权衡种群的收敛性和多样性,在保证收敛性的同时会降低多样性,导致容易陷入局部最优,降低最优原子的搜索速度. 表中对应的MSE为30次实验平均值. 3.2.2匹配追踪稀疏去噪性能 图2 山斑鸠声音信号与去噪后声音信号Fig.2 The original signal and the denoised signal of Rufous Turtle Dove (20) (21) 其中:λ为帧索引;Psignal(λ)为原信号功率谱;Pdenosied(λ)为加噪声音信号进行去噪操作后的信号功率谱;κ为帧数. 实验结果如表3所示. 分析表3,当背景噪声为高斯白噪声时,匹配追踪法去噪效果优于谱减法和小波法; 当背景噪声为雷声时,匹配追踪法去噪效果介于谱减法和小波法之间; 而在风声和流水声情况下,匹配追踪法相比谱减法和小波法去噪效果更显著. 这些去噪性能上的差异是由于匹配追踪法去噪利用待检测信号与背景噪声稀疏度的差异,当背景噪声与前景声有较多频域重叠时,稀疏度差异不大,部分噪声也完成重构,去噪性能有所降低. 综合来看,基于稀疏性的匹配追踪法去噪不需要相关统计特性作为先验知识,能够自适应去除多种类型噪声. 表3 使用不同算法的降噪性能对比 3.2.3复合特征有效性检验 图3 四种声音类别的4个特征集识别精度Fig.3 Recognition accuracy comparison of 4 feature sets of 4 sound categories 为验证本研究特征对生态声音识别的适用性,选取研究方向相近的文[4-5]和文[7],利用使用径向基核函数(RBF)的支持向量机作为分类器进行实验对比. 支持向量机(support vector machine,SVM)是Vapnik等人在多年研究统计学习理论的基础上,根据统计学习理论中结构风险最小化原则提出的一种可训练的线性分类器,通过寻找最优分类超平面对应的判别函数,实现样本识别与分类,在解决小样本、 非线性及高维模式识别中表现出许多特有优势. 在进行SVM模型训练前,将所有用于训练的声音所提取的特征进行均方归一化后生成特征训练矩阵以及对应的分类标签. 利用Libsvm工具箱对所有训练声音段选取前50帧采用交叉验证方式确定最佳的惩罚因子c和核函数参数g,对整个训练矩阵进行训练获取SVM判别模型. 实验结果如图3所示. 从种类间对比和特征对比两个角度出发,4种声音类别中,鸟叫声识别率相对最高,平均81.38%,昆虫叫声识别率较低,平均71.73%. 综合4种特征对所有类别声音的识别性能看,本方法特征识别率优于其他三种特征达到81.06%. 由于单独使用本文所提取的MP特征, 特征维数过少, 整体识别率偏低,平均仅16.82%,单独使用一维PITCH特征,效果微乎其微,不具备实际意义,与其他组特征没有可比性. 在 MFCCs特征基础上单独结合MP时频特征,相比单独使用MFCCs特征,识别率平均增加6.08%,再结合PITCH特征识别率平均增加0.94%. 实验结果表明, MP特征和PITCH特征对MFCCs特征的识别能力有增益作用,其中前者贡献最大. APNCCs特征在鸟类声音识别方面表现不俗,但对其他三种声音类别的识别率平均低于本文特征5.55%. 3.2.4模拟自然环境下的生态声音识别有效性检验 选取风声、 流水声、 雷声3种自然噪声以及高斯白噪声作为背景噪声,利用小波法和谱减法分别对带噪声音信号去噪后提取的MFCCs和PITCH特征参数用于和本方法进行对比验证. 图4给出了在不同背景噪声情境下,对应于40~10 dB信噪比范围内,3种不同去噪方法分别使用SVM分类器模型获得的识别率均值对比. 不同背景噪声对不同方法的识别率造成不同程度的影响,总体上,随着信噪比的降低,识别率呈下降趋势,三种自然噪声在40~10 dB范围内,下降趋势相对平缓,而信噪比低于10 dB时,识别率大幅下降. 风声与流水声情况下,当信噪比在0~30 dB范围时,本研究方法识别率高于另外两种方法,信噪比大于30 dB时,谱减法性能更好一些; 雷声情况下,噪声对匹配追踪法的影响较为显著,谱减法总体识别率更高. 而高斯白噪情况下对应的三种方法总体识别率都偏低,匹配追踪法复合特征的识别率优于另外两种. 在信噪比降低至-10 dB时,由于噪声信号对原始信号干扰过大,三种方法的识别率均达到谷底. 综合分析,基于混合优化的匹配追踪法在低信噪比情况下抗噪性更好. 图4 四种噪声下不同信噪比SVM的识别率均值对比 4结语 采用GSO+PSO的混合优化算法搜索最优原子的策略能够有效地减少匹配追踪算法的计算复杂度. 基于稀疏性的匹配追踪算法去噪提高了生态声音识别的抗噪性能,较之谱减法和小波法去噪,在多种场景下也具有一定优越性. 实验表明,复合特征在低信噪比的自然生态场景中,对识别系统抗噪性和鲁棒性的提高更为显著. 下一步工作着重于将该方法推广应用到微弱信号,或信噪比更低的复杂条件下,其他自然生态声音的识别与分类. 参考文献: [1] CHU S, NARAYANAN S, KUO C C J. Environmental sound recognition with time-frequency audio features[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2009, 17(6): 1 142-1 158. [2] CHEN W P, CHEN S S, LIN C C,etal. Automatic recognition of frog calls using a multi-stage average spectrum[J]. Computers & Mathematics with Applications, 2012, 64(5): 1 270-1 281. [3] LEE C H, HSU S B, SHIH J L,etal. Continuous birdsong recognition using gaussian mixture modeling of image shape features[J]. IEEE Transactions on Multimedia, 2013, 15(2): 454-464. [4] RAJU N, MATHINI S, PRIYA T L,etal. Identifying the population of animals through pitch, formant, short time energy-A sound analysis[C]//Proceedings of International Conference on Computing, Electronics and Electrical Technologies. N J: IEEE Piscataway, 2012: 704-709. [5] MATHINI S, RAAJAN N R, RAJU N,etal. Distance analysis and population calculation from sound produced by animals[J]. Procedia Engineering, 2012, 38: 994-1 000. [6] VERMA N, VERMA A K. Real time adaptive denoising of musical signals in wavelet domain[C]// Nirma University International Conference on Engineering. N J: IEEE Piscataway, 2012: 1-5. [7] YAN Xin, LI Ying. Anti-noise power normalized cepstral coefficients in bird sounds recognition[J]. Acta Electronic Sinica, 2013, 41(2): 295-300. [8] LI S, FANG L. Signal denoising with random refined orthogonal matching pursuit[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(1): 26-34. [9] YAMAKAWA N, TAKAHASHI T, KITAHARA T,etal. Environmental sound recognition for robot audition using matching-pursuit[M]. Heidelberg: Springer, 2011: 1-10. [10] SIVASANKARAN S, PRABHU K M M. Robust features for environmental sound classification[C]// IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT). N J: IEEE Piscataway, 2013: 1-6. [11] KRISHNANAND K N, GHOSE D. Glowworm swarm optimization for multimodal search spaces[J]. Handbook of Swarm Intelligence: Concepts, Principles and Applications, 2011(8): 451-467. [12] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. N J: IEEE Piscataway, 1995: 1 942-1 948. [13] Universitat Pom peu Fabra. Repository of sound under the creativecom m ons license[DB/OL]. (2012-5-14)[2013-10-20]. http://www.freesound.org. [14] LI M, LI Y. Ecological environmental sounds classification based on genetic algorithm and matching pursuit sparse decomposition[C]// Proceedings of 5th International Congress on Image and Signal Processing. N J: IEEE Piscataway, 2012: 1 439-1 443. (责任编辑: 沈芸) Ecological sounds recognition based on hybrid optimized matching pursuit LI Biyu,LI Ying (College of Mathematics and Computer Science, Fuzhou University, Fuzhou,Fujian 350116, China) Abstract:The paper proposes an anti-noise ecological sounds identification system by using hybrid optimized matching pursuit (MP) method. Firstly, using the MP to decompose the sound signal sparsely, reconstruct its high correlation structure and reduce the low correlation noise. Hereinto, glowworm swarm optimization(GSO) and particle swarm optimization (PSO) are employed to speed up the process of MP decomposition. Then, anti-noise composite feature sets are extracted according to the time-frequency information of optimal atoms and the MFCCs. Finally, through the support vector machine (SVM) classifier, 40 classes of ecological sounds are tested for the comparison experiments in different environments under different SNRs. Compared with spectral subtraction and wavelet de-noising, the MP owns the best performance for de-noising. The experimental results show that this approach outperforms traditional method of MFCCs, as the average identification accuracy and robustness for ecological sounds are improved to a different degree. Keywords:ecological sounds recognition; matching pursuit; signal reconstruct; glowworm swarm optimization; particle swarm optimization DOI:10.7631/issn.1000-2243.2016.03.0405 文章编号:1000-2243(2016)03-0405-09 收稿日期:2014-08-30 通讯作者:李应(1964-),教授,主要从事声音识别研究,fj_liying@fzu.edu.cn 基金项目:国家自然科学基金资助项目(61075022) 中图分类号:TP391.42 文献标识码:A