基于二维最小二乘回归的子空间分割

刘展杰，陈晓云

(福州大学数学与计算机科学学院, 福建 福州　350116)

基于二维最小二乘回归的子空间分割

刘展杰，陈晓云

(福州大学数学与计算机科学学院, 福建 福州350116)

摘要：现实中有很多样本数据是二维的，且多数聚类方法需将二维样本数据向量化，从而导致二维数据的内部几何信息丢失. 针对这一问题，提出二维最小二乘回归子空间分割方法直接对二维数据进行聚类, 将一维最小二乘回归子空间分割方法推广到二维，使得原始数据的结构信息得以保留. 在人脸数据集和哥伦比亚大学图像数据集上进行实验，结果表明该方法是有效的.

关键词：聚类； 最小二乘回归； 子空间分割； 二维样本

0引言

随着计算机及网络应用的不断发展，越来越多的多维样本数据被产生，如图像、 视频. 现有的许多方法在处理数据之前，需要将一幅图像或一段视频表示成一维向量，即用32×32二维矩阵表示的图像按行(或列)连接成1×1 024的一维向量. 若这类样本具有特殊的空间结构，对其做向量化处理难以避免地会导致数据信息的损失. 针对这类不足，近年来许多学者开始研究如何将样本向量的输入形式转化成原二维矩阵的输入形式，甚至是更高维的形式. 比如经典的子空间学习方法LDA[1]和PCA[2]等都有上述不足，因此2D-PCA[3]、 2D-LDA[4]、 MPCA[5]等方法被提出，且都取得较好的实验结果.

子空间分割又称子空间聚类，被广泛应用到运动分割[6-7]、 图像聚类[6-9]等. 子空间分割方法已经在图像研究领域取得了巨大成功[6-9]. 将同类图像视为一个子空间，利用子空间分割方法对图像数据进行聚类，其中典型的子空间分割方法有稀疏表示子空间分割(SSC)[6]、 低秩表示子空间分割(LRR)[7]、 最小二乘回归子空间分割(LSR)[8]等. 除此之外，层次聚类(HC)[10]、 自组织映射(SOM)[11-12]和非负矩阵分解(NMF)[13]及其扩展模型[14-16]等也成功应用于图像数据聚类，但非负矩阵分解要求所处理的矩阵对象非负，这无疑限制了NMF的应用.

无论是子空间分割方法还是非负矩阵分解法，共同的缺陷就是需要将二维矩阵样本或更高维样本向量化. 针对这一问题，推广了最小二乘回归子空间分割方法(LSR)[15]，提出二维最小二乘回归子空间分割方法(two-dimensional least square regression, 2D-LSR).

1子空间分割

子空间分割是聚类问题研究的热点，已经成功应用在机器学习和机器视觉等领域[6-8].

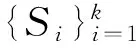
许多子空间分割方法已经被提出，根据不同的算法可粗略分为四类[8]： 代数方法、 迭代方法、 统计方法和谱聚类方法. 更多的子空间分割方法参见综述[9]. 本文重点研究基于谱聚类的子空间分割方法.

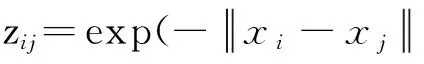
(1)

LSR的目标函数是最小化Z的Frobenius范数：

(2)

对于有噪声的模型，可以扩展为：

(3)

去掉限制条件diag(Z)=0，还可以扩展为：

(4)

文献[8]的实验结果显示，SSC，LRR和LSR三者中，LSR运行的时间最少，且LSR是鲁棒的，有较好的聚集性能并且可以得到解析解，可以快速得到表示系数[8]. 但是针对样本为矩阵数据的聚类问题，便要将其向量化，为此提出二维最小二乘回归子空间分割方法(2D-LSR).

2二维最小二乘回归子空间分割

由n个二维矩阵样本Xi(i=1, 2, …,n)组成的原始数据集为XM=[X1, …, Xn]∈d1×(d2n)，将所有图像按一行排过去. 向量化后变成XV=[x1, …,xn]∈d×n，其中d1×d2=d，n为样本数. 对于矩阵向量化后的数据，容易失去样本内部结构的几何信息，影响聚类效果.

2.12D-LSR目标函数

由式(1)推广：

(5)

将原来一维的模型推广到二维的. Zij是一个矩阵，其现实意义是对矩阵的每个点都赋予一个权重.

且根据线性LSR模型(4)可知：

(6)

其中： Zi=[zi1, …,zin]T∈n；xi∈d(i=1, …,n).

由于模型(6)中的xi是一行向量，若以二维矩阵样本Xi作为输入，则模型(6)需推广如下：

(7)

由(7)式得出2D-LSR目标函数为：

(8)

(9)

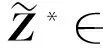
(10)

(11)

模型(8)与模型(6)对比，模型(6)的解析解为：

(12)

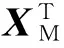
2.22D-LSR算法

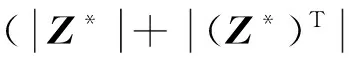
算法： 二维最小二乘回归子空间分割算法.

Input： 数据矩阵X∈d1×d2n，正则参数λ，类数k.

Output：k个类簇.

Step1： 利用公式(9)和(11)解2D-LSR问题，求得Z*；

Step3： 应用标准分割方法将数据分成k个子空间.

值得注意的是，算法输入的类别数k都是事先已知的，即实验的数据集都带有类标签，因此实验也不讨论k的选择.

3实验

实验在Win7系统，2G内存环境下完成，所有方法都用Matlab2010b编程实现. 为验证 2D-LSR方法的有效性，将2D-LSR和LSR[8]、LRR[7]两种线性子空间分割方法以及传统的K均值(K-means)[18]和层次聚类(HC)[6]算法的聚类准确率进行对比. 聚类准确率采用文献[18-19]的计算方法，2D-LSR、LSR和LRR的正则参数为{0.000 1, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 5, 10}. 为避免随机性，每种方法运行50次，取平均值作为最终聚类准确率.

3.1数据集

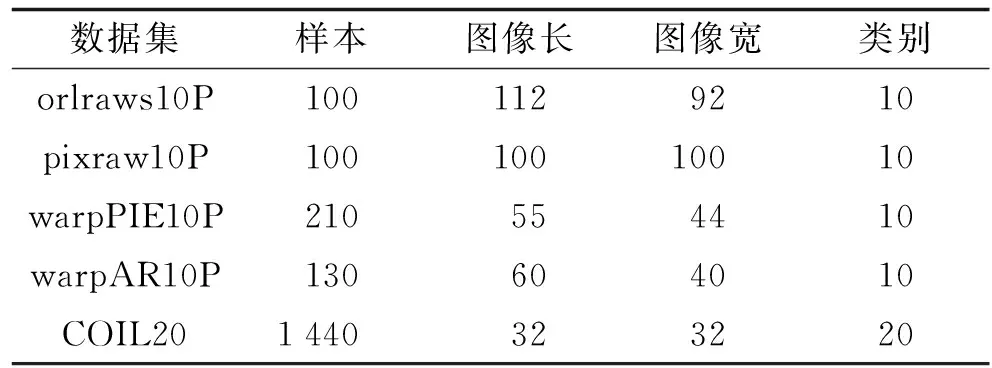
表1　数据集描述

选用4个人脸图像数据集和哥伦比亚图像数据集. 4个人脸图像数据集分别是orlraws10P、 pixraw10P、 warpPIE10P和warpAR10P, 这些数据集来自http://featureselection.asu.edu/datasets.php； 哥伦比亚大学图像数据(COIL20)[20]包含20个对象(类)，每个对象在水平上旋转360°，每隔5°拍摄一张照片，因此每个对象共72幅图，每个图像的大小是32×32像素, 像素灰度值为256. 这5个数据集的共同点是每张图片都由向量表示，每条向量的长度是图像长与宽的乘积. 将5个数据集整理归纳在表1. 实验将向量恢复成矩阵的形式，并且对数据进行标准化，即

(13)

受到实验环境的限制，对每个数据集只取每类的前5个样本数据作为实验样本.

3.2实验结果与分析

实验结果如表2所示，为避免随机性，每种方法运行50次取聚类准确率的均值±方差(正则参数λ). 值得注意的是，LSR、 LRR和2D-LSR的准确率是取所有参数中最好的结果.

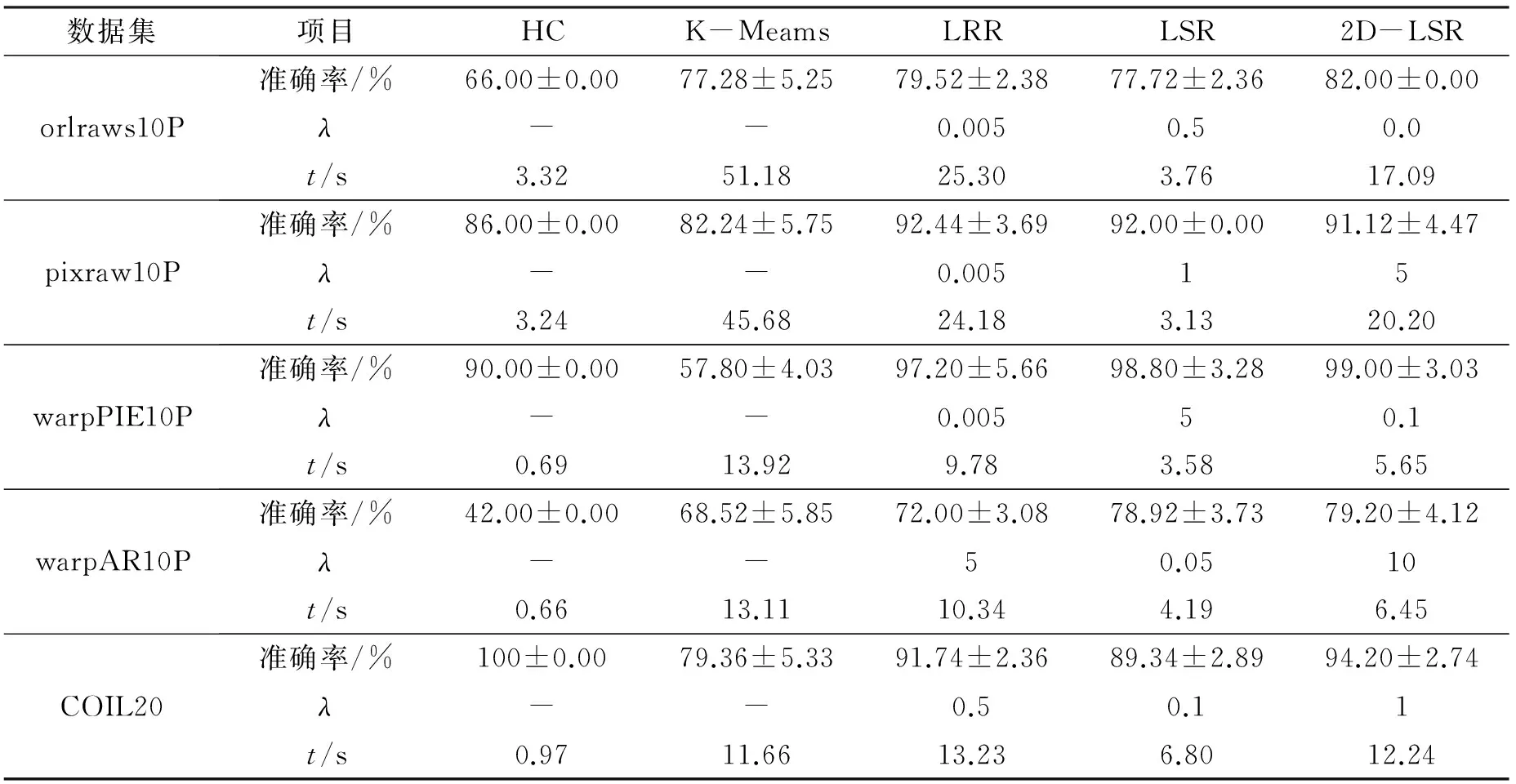
表2　聚类准确率和运行时间的对比

由表2的实验结果发现： 在算法聚类质量方面，2D-LSR在所有测试数据集上都取得了较好的聚类效果. 在5个数据集中的3个2D-LSR的聚类准确率最高，在pixraw10P上比LRR和LSR略低，在COIL20则仅低于HC算法. 对比2D-LSR和LSR，2D-LSR在orlraws10P、 pixraw10P、 warpPIE10P和warpAR10P 上的准确率均高于LSR，特别在orlraws10P和COIL20上2D-LSR准确率比LSR高出5%. 在时间方面，大部分情况下HC是最快的，K-means是最慢的. 2D-LSR与LSR相比，后者更快，这是由于二者计算复杂度不一样所致； 但是2D-LSR与LRR相比，前者更快. 且随着数据集图像大小的变化，5种算法都会受到一定程度的影响，且LSR受的影响较小. 说明在维数高的图像上，各个算法会更耗时； 而对于维数小的图像上，算法需要识别处理的数据少，从而提升算法的运行时间.

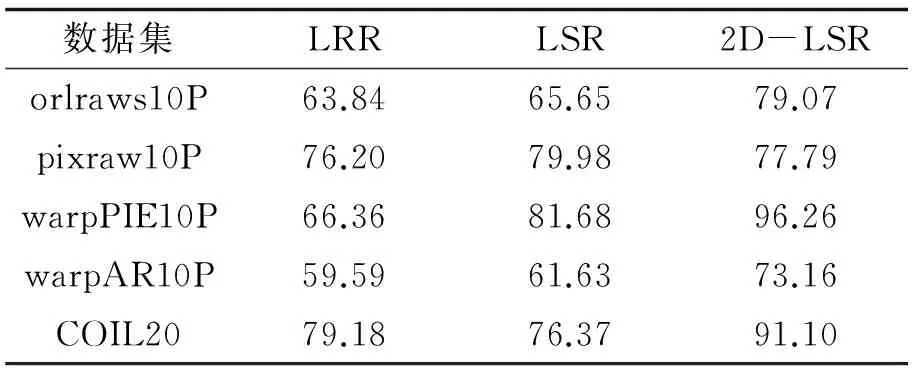
表3　比较不同参数下的平均聚类准确率

由上可知，2D-LSR算法不能同时保证算法准确率高和运行时间快. 为了权衡算法的准确率与效率，比较实验方法的稳定性，10个不同参数下的整体稳定性，表3列出不同参数下所获得的聚类准确率的均值.

可以看出，在pixraw10P数据，2D-LSR的聚类准确率略低于LRR和LSR的准确率； 而在另外4个数据里，2D-LSR的聚类准确率明显高于LRR和LSR. 这说明2D-LSR比LRR和LSR更稳定，整体效果更好.

3.3参数选择

2D-LSR算法与LSR、 LRR算法一样，都仅有一个正则参数λ. 对于2D-LSR与LSR，正则参数起到能够降低样本相关性的作用. 图1描述了3种算法在人脸数据集下，参数λ的变化对聚类准确率的影响. 可以从整体观察聚类准确率受参数不同取值的影响. 参数λ为0.005和1附近，LRR的聚类效果较为理想； 参数λ为0.1～1之间时，2D-LSR和LSR的聚类效果较为理想； 当参数λ<0.1时，LSR的准确率较低，甚至比LRR低，这与文献[8]的结论是一致的. 在所有除pixraw10P外其它数据集上，2D-LSR在不同参数下的准确率最稳定，受λ取值影响最小.

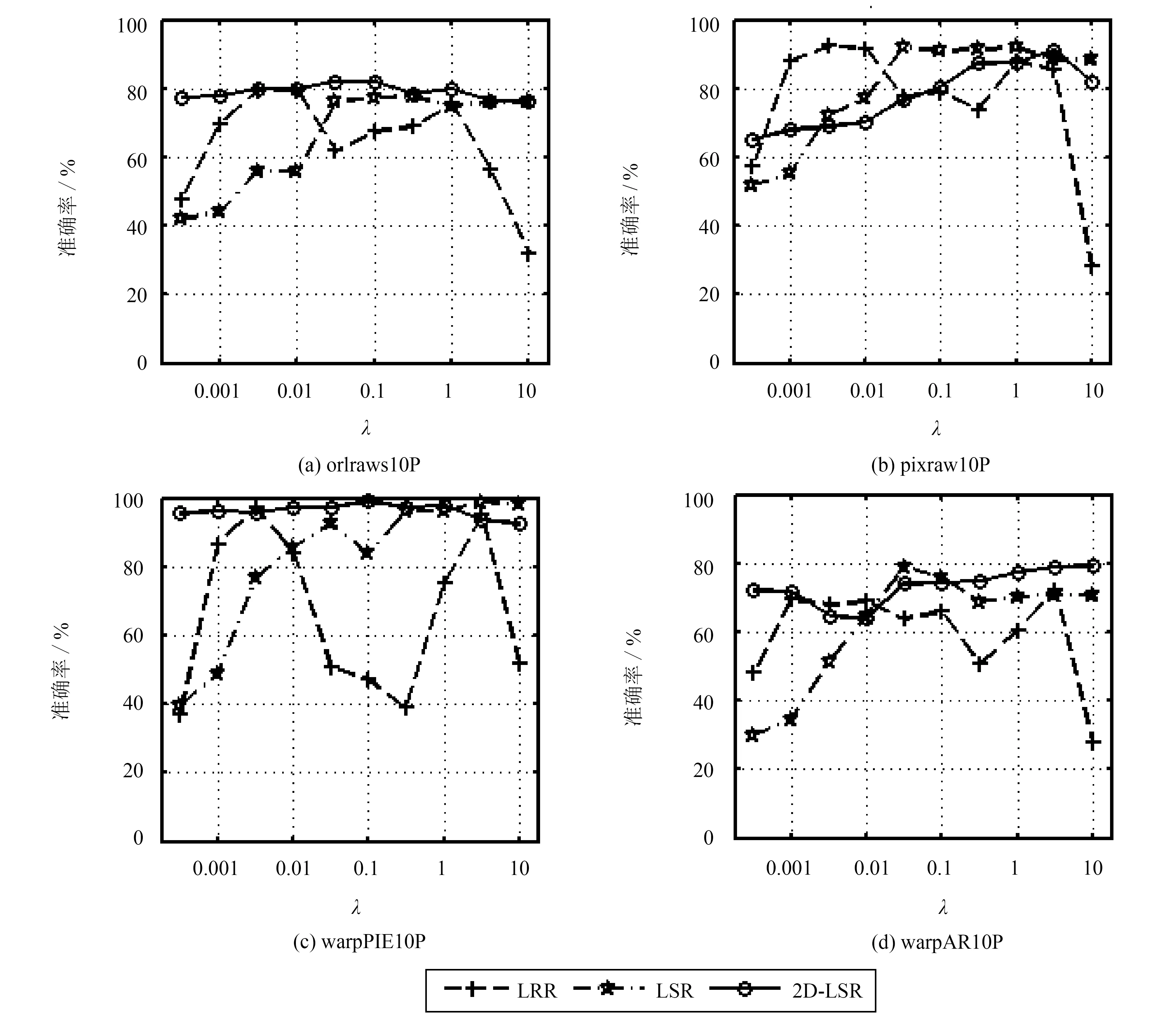
图1　人脸数据集中不同参数下的聚类结果Fig.1　The results of accuracy with different parameters setting on face databases

4结论

提出二维最小二乘回归子空间分割方法(2D-LSR)，并将其成功应用于二维图像样本数据的聚类. 实验结果表明, 2D-LSR可以很好地刻画二维数据的结构信息且具有良好的聚合能力. 虽然在运行时间上处于劣势，但是与现有的LSR、 LRR子空间分割模型相比，2D-LSR更稳定、 更精确，是一种有效的二维矩阵样本集聚类算法. 当然, 2D-LSR也存在如何高效选取正则参数的问题，将在以后的研究中给出.

参考文献：

[1] WOLD S, ESBENSEN K, GELADI P. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2(1): 37-52.

[2] FISHER R A. The use of multiple measurements in taxonomic problems[J]. Annals of Eugenics, 1936, 7(2): 179-188.

[3] YANG J, ZHANG D, FRANGI A F,etal. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2004, 26(1): 131-137.

[4] LI M, YUAN B. 2D-LDA: a statistical linear discriminant analysis for image matrix[J]. Pattern Recognition Letters, 2005, 26(5): 527-532.

[5] LU H, PLATANIOTIS K N, VENETSANOPOULOS A N. Multilinear principal component analysis of tensor objects for recognition[C]//Proceedings of the 18th International Conference on Pattern Recognition. Hong Kong: [s.n.], 2006: 776-779.

[6] ELHAMIFAR E, VIDAL R. Sparse subspace clustering[C]//Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Miami: IEEE，2009: 2 790-2 797.

[7] LIU G, LIN Z, YU Y. Robust subspace segmentation by low-rank representation[C]//Proceedings of the 27th International Conference on Machine Learning (ICML). Haifa: [s.n.], 2010: 663-670.

[8] LU C Y, MIN H, ZHAO Z Q,etal. Robust and efficient subspace segmentation via least squares regression[C]//12th European Conference on Computer Vision-ECCV. Florence： Springer, 2012: 347-360.

[9] VIDAL R. A tutorial on subspace clustering[J]. IEEE Signal Processing Magazine, 2010, 28(2): 52-68.

[10] JOHNSON S C. Hierarchical clustering schemes[J]. Psychometrika, 1967, 32(3): 241-254.

[11] KOHONEN T. The self-organizing map[J]. Proceedings of the IEEE, 1990, 78(9): 1 464-1 480.

[12] TAMAYO P, SLONIM D, MESIROV J,etal. Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation[J]. Proceedings of the National Academy of Sciences, 1999, 96(6): 2 907-2 912

[13] LEE D D, SEUNG H S. Algorithms for non-negative matrix factorization[C]//Proceedings of Neural Information Processing Systems. Denver: [s.n.], 2001: 556-562.

[14] GAO Y, CHURCH G. Improving molecular cancer class discovery through sparse non-negative matrix factorization[J]. Bioinformatics, 2005, 21(21): 3 970-3 975

[15] WANG Y, JIA Y. Fisher non-negative matrix factorization for learning local features[C]//Proceedings of the Sixth Asian Conference on Computer Vision. Jeju: [s.n.], 2004: 27-30.

[16] BRUNET J P, TAMAYO P, GOLUB T R,etal. Metagenes and molecular pattern discovery using matrix factorization[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(12): 4 164-4 169

[17] SHI J, MALIK J. Normalized cuts and image segmentation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2000, 22(8): 888-905.

[18] CAI D, HE X, WU X,etal. Non-negative matrix factorization on manifold[C]//Proceedings of the 8th IEEE International Conference on Data Mining. Pisa: [s.n.], 2008: 63-72.

[19] MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]//Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Los Angeles: [s.n.],1967, 1: 281-297.

[20] CAI D, HE X, HAN J,etal. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1 548-1 560.

(责任编辑： 洪江星)

Two-dimensional least square regression based subspace segmentation

LIU Zhanjie, CHEN Xiaoyun

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

Abstract:In reality, most of data is two-dimensional, and most of clustering methods process the data with vectorization first. This practice leads to loss internal geometry information of data. To solve this problem, a two-dimensional least square regression method based subspace segmentation is put forward for clustering on 2-dimensional data. 1-dimensional space is extended to 2-dimensional space, and it keeps the structure information of original data. Experimental results show that this method is effective on face databases and the Columbia University Image Library.

Keywords:clustering; least square regression; subspace segmentation; 2-dimensional space

DOI:10.7631/issn.1000-2243.2016.03.0431

文章编号：1000-2243(2016)03-0431-06

收稿日期:2014-12-18

通讯作者:陈晓云(1970-)，教授，主要从事数据挖掘、 模式识别等方面的研究，c_xiaoyun@21cn.com

基金项目：国家自然科学基金资助项目(71273053)； 福建省自然科学基金资助项目(2014J01009)

中图分类号：TP311； TP371

文献标识码：A