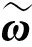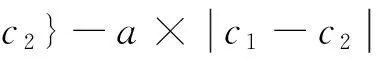常值初始化的自适应活动轮廓模型

郭雅彬，王美清

(福州大学数学与计算机科学学院，福建 福州　350116)

常值初始化的自适应活动轮廓模型

郭雅彬，王美清

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：李纯明提出的水平集方法(LI模型)很好地解决了测地活动轮廓模型(GAC)的重新初始化问题，但该模型对边缘信息较弱或者灰度不均匀的图像分割结果仍然不理想. 针对这些问题，提出常值初始化的自适应活动轮廓模型，该模型中自适应力的系数包含了图像的灰度信息，从而提高了活动轮廓在演化过程中对模糊边界的识别能力； 同时，重新定义的外部能量，避免过分割现象. 实验结果验证了模型的有效性.

关键词：图像分割； 活动轮廓； 自适应； 权重系数

0引言

基于偏微分方程的几何活动轮廓模型方法可以获得具有连续闭合性、 精确度高的目标边界, 因此得到了广泛的研究[1]. 该类方法在演化曲线上定义一个能量泛函，通过最小化该能量泛函来驱动曲线朝目标边界进行演化. 基于偏微分方程活动轮廓模型可分为基于边界的模型[2-4]和基于区域的模型[5-9].

测地活动轮廓模型(geodesic active contour, GAC)是基于曲线演化和水平集理论的，其最大的特点是不依赖于曲线参数，可以灵活处理曲线的拓扑结构变化. 通常初始水平集取为符号距离函数, 但是其在演化过程中不能保持, 违背了水平集方法的理论，需要周期性重新初始化，导致效率低下. 李纯明等[10-11]提出了无需重新初始化的改进方案，并在GAC模型上进行验证. 将无需重新初始化的GAC模型称为LI模型. 具体是在能量泛函中添加了一项内部能量项用来纠正水平集函数与符号距离函数的偏差，替代了周期性的初始化过程，这是传统方法的重大突破. 此外，该方法可以采用简单的有限差分法和较大的时间步长求解相应的偏微分方程，极大地提高了水平集演化的速度. 然而，这种方法并没有改变GAC模型演化曲线单向运动对初始轮廓敏感的缺点，对边缘信息较弱的灰度不均匀图像不能得到准确分割. 主要原因是由GAC作为外部能量泛函的权系数为常数，不能根据图像自适应地调整符号和大小，只利用边缘信息使得对于边缘信息较弱的灰度不均匀的图像难以得到准确的分割结果.

针对这个原因提出了可变权系数和新的外部能量泛函，其具有自适应力的双向性、 抗噪性和提高处理灰度不均匀图像的能力，随着迭代次数的增加均能稳定在边界上. 模型主要提取皮肤病变区的边界和乳腺造影图的外部轮廓.

1相关背景

1.1测地活动轮廓模型(GAC)

GAC模型是通过最小化以下能量泛函来确定活动轮廓：

(1)

(2)

式中：K是用于控制函数g(·)的下降速度的选定参数.

使用变分法最小化式(1)得到其对应的梯度下降流. 即曲线演化方程为：

(3)

式中： k为曲线曲率； N为指向曲线内部的单位法向量.

定义水平集φ为符号距离函数，利用变分水平集方法，得到GAC模型的曲线演化方程对应水平集函数φ的PDE方程为：

(4)

该模型存在一个缺陷，当图像中有较深的凹形边界时，可能使曲线停在某一能量局部极小值状态，而无法向真实边界逼近. 因此Caselles等[3]提出了推广的GAC模型，其梯度下降流为

(5)

式中c为一个常数，根据具体的图像来进行设置. 对应水平集函数φ的PDE方程为

(6)

与式(4)比较，改进的模型中引进了一个收缩力gcN，收缩力受到g的控制，方向总是指向曲线内部. 推广的GAC模型能正确检测凹陷边界但易出现过分割. 数值计算过程中需要周期性地重新初始化水平集函数，导致计算效率低.

1.2LI模型

传统水平集函数在演化过程中需要周期性地初始化演化曲线，这样违背了水平集方法的理论而且效率低. 为了克服周期性重新初始化水平集函数的缺点，李纯明等[10-11]提出了一种新的无需重新初始化的水平集方法. 该模型的能量泛函定义为：

(7)

其中：λ>0;ν为参数；g为边缘停止函数，通常取为g(s)=(1+s2)-1；H为Heaviside函数； δ为Dirac函数.

该模型的第一项用来纠正水平集函数与符号距离函数的偏差，从而实现了水平集保持在距离函数的附近，使得演化过程无需重新初始化； 第二项和第三项组成了外部能量项，其中第二项是加权长度项，保证演化曲线的光滑； 第三项为加权面积项，使得曲线收缩到目标边界.

通过变分法极小化能量泛函E(φ)，可以得到相应的水平集演化方程：

(8)

该方法有效地避免了重新初始化问题，但曲线演化方向主要通过参数ν的选取控制. 当ν<0，曲线向外扩张； 当ν>0，曲线向内收缩. 所以初始曲线只能设置在目标内部或者目标外部，无法自适应地调节曲线演化的方向，且对噪声敏感.

1.3LI模型的相关改进

为克服LI模型的单向运动，文献[12-13]提出了改进模型，主要思路为修改外部能量项中面积项的系数ν，使之能根据图像信息来驱动曲线演化.

2常值初始化的自适应水平集演化

2.1常值初始化的自适应活动轮廓模型

文献[12-13]所提的方法，在一定程度上克服了LI模型演化的单向性和对噪声的敏感性，但其仍存在对灰度不均匀的图像分割不准确，易产生边缘泄露的缺点. 为解决这些问题，提出一个新的包含图像信息的可变权系数：

(9)

其中：c1,c2分别为曲面内外部的灰度均值；a∈(0, 1)为权衡分割弱边缘权衡系数. 下面用定理来说明所提出的可变权系数ν(I)具有双向性.

(10)

(11)

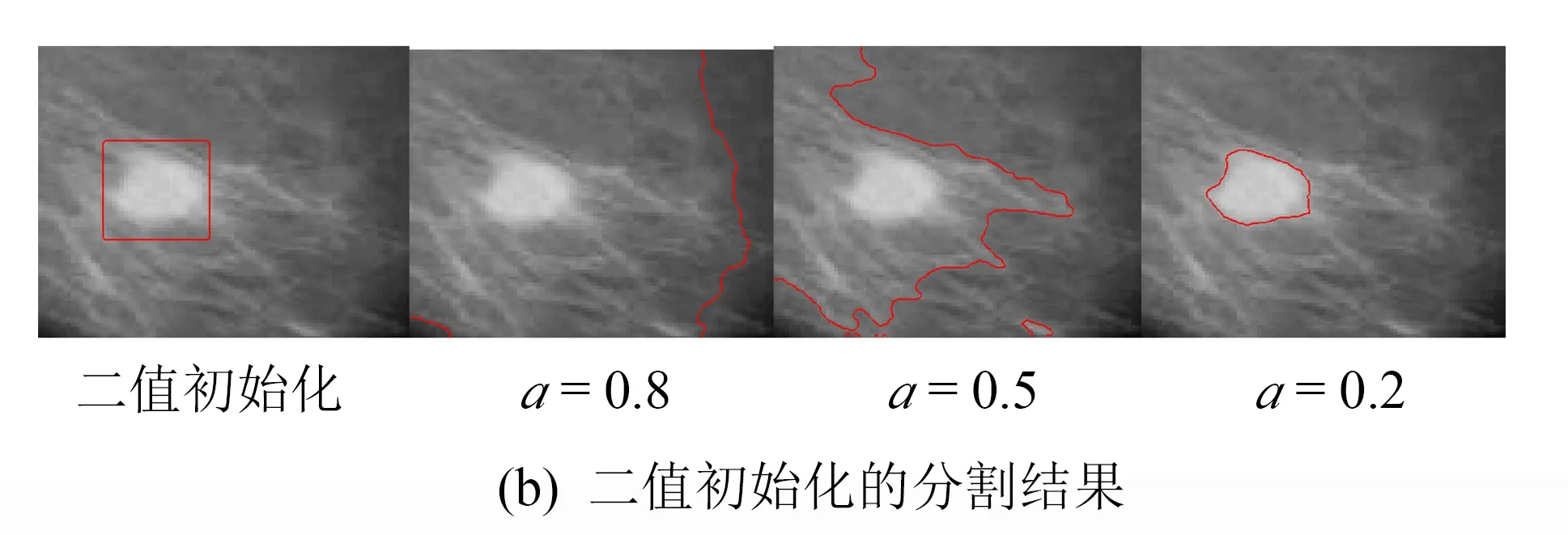
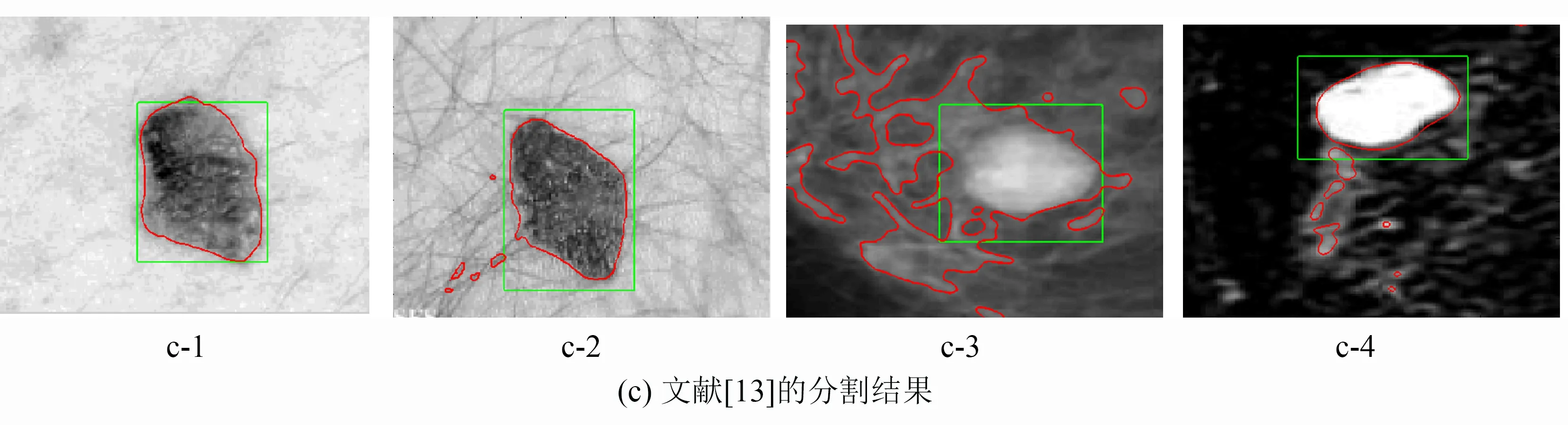
当c1

(12)

又因为

所以

(13)

(14)

(15)

定理得证.

表达式(14)和(15)说明了包含图像灰度信息的可变权系数ν(I)可根据演化曲线的位置自动改变符号. 当演化曲线位于目标内部时ν(I)<0，向外扩张； 当演化曲线位于目标外部时ν(I)>0，向内收缩. 因此ν(I)具有双向性，克服了LI模型演化曲线的单向性.ν(I)的方法简单，不含导数，无需特殊的离散化方法，数值计算稳定.

2.2权重系数a的确定与常值初始化

由于a可指示出分割目标的边界，所以当轮廓远离边界时，模型的演化外力仍然可以捕获到正确的边界，那么模型的初始轮廓就可以取为整幅图像，即初始的水平集函数取为常值函数.

2.3外部能量泛函

图1　模型分割结果Fig.1　Segmentation result of the proposed model

在LI模型中，边缘停止函数g起到的作用是让演化曲线稳定在边界上. 本文提出的ν(I)同样具有稳定边界的效果，那么g仅相当于是加权函数，由g的性质易知0

(16)

因此，总能量泛函为：

(17)

通过变分法极小化能量泛函E(φ)，得到相应的水平集演化方程：

(18)

3实验结果与分析

以下实验中偏微分演化方程的离散化方法采用中心差分格式，参数分别设置为ε=1.5，λ=8.2，Δt=5，μ=0.04，权重系数a，根据对目标物体的轮廓或者细节需求的不一样进行设置. 在没有特别说明的情况，初始轮廓均常值初始化为φ=2.

3.1权重系数a的影响和常值初始化

图2显示了一幅真实图像在a取不同值时的分割结果. 从图2中可以看出，不管是在常值初始化还是二值初始化，只在a=0.2的时候得到正确的结果. 所以正是由于a的选取，才使得模型可以将初始轮廓简单的设为常值函数. 同时可以看出当a取值越小时，分割出的目标区域包含的黑色区域越少，而白色区域越多. 可知，当目标像素值较大时，a应取小于0.5的数； 反之，取大于0.5.

图2　a对模糊边界分割位置的影响

3.2初始演化曲线位置的敏感性

图3中第一列(图3a)为初始轮廓，第二列(图3b)、 三列(图3c)分别为ν=-2，ν=2时LI模型的分割结果，第四列(图3d)为文献[14]的分割结果，第五列(图3e)为本文模型a=0.3的分割结果. 结果显示，采用LI模型，只有当曲线完全包围目标时，才得到了正确分割，除此之外无论ν>0或ν<0，都不能得到正确的分割结果； 文献[14]在初始轮廓曲线在目标内能够得到准确的分割结果，当初始轮廓曲线包含目标或与目标交叉时，实验结果均出现过分割现象； 而采用本文模型，初始轮廓无论设置在何处，均能从不同方向自适应地收敛目标边界.

图3　常值初始化的自适应活动轮廓模型对任意轮廓的自适应性Fig.3　The adaptability of the proposed model of arbitrary profile

3.3分割效果比较

图4显示了LBF模型、 文献[4]、 文献[13]、 本文模型对两幅真实的皮肤病变图像和两幅乳腺造影图像的分割结果，其中绿色曲线为初始轮廓，红色曲线为分割结果. 由图中可以看出，LBF模型(见图4a)对于所给的图像都不能正确分割，易陷入局部极小值； 文献[4]的模型(见图4b)除对图4(b-4)能正确分割外，其他图像均未的得到正确结果，且其分割的次数均为几千次； 文献[13]的模型(见图4c)除对图4(c-1)能正确分割外，其他图像均未的得到正确结果； 而本文模型(见图4d)在所给的图像均得到理想的分割效果. 实验中参数a分别为0.6、 0.7、 0.25、 0.1，迭代次数分别为15、 100、 130、 30.

图4　LBF模型、 文献[4]、 文献[13]与本文模型的对比

3.4分割结果的稳定性

图5分别为文献[13]和本文算法的分割结果，取同样的初始轮廓线，可以看出文献[13]所提的模型随着迭代次数的增加，轮廓越来越向内收缩. 而本文模型经过迭代5 000次后依然能很好地保持边界.

图5　本文模型分割结果稳定性的验证Fig.5　Verify the stability of the segmentation results of the proposed method

4结论

自适应常值初始化水平集演化方法实现了对高噪声、 弱边缘图像的分割. 实验结果表明了该方法演化具有双向性，也可将初始轮廓曲线简单初始化为常值函数； 模型中的权重系数a可控制模糊边界的分割位置，提高了处理非同质图像的能力； 重新定义了外部能量泛函，可以得到稳定分割的实验结果. 但是权重系数a是根据不同分割位置的需求人为设置的，因此下一步将在这方面做进一步的研究.

参考文献：

[1] 王大凯, 侯榆青, 彭进业. 图像处理的偏微分方程方法[M]. 北京: 科学出版社, 2008: 80-108.

[2] KASS M, WITKIN A, TERZOPOULOS D. Snakes: active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331.

[3] CASELLES V, KIMMEL R, SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61-79.

[4] 林震梅. 测地轮廓模型的改进模型及数值算法的加速[D]. 福州: 福州大学, 2012.

[5] MUMFORD D, SHAH J. Optimal approximations by piecewise smooth functions and associated variational problems[J]. Communications on Pure and Applied Mathematics, 1989, 42(5): 577-685.

[6] VESE L A, CHAN T F. A multiphase level set framework for image segmentation using the mumford and shah model[J]. International Journal of Computer Vision, 2002, 50(3): 271-293.

[7] CHAN T F, VESE L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266-277.

[8] LI C, KAO C Y, Gore J C,etal. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Transactions on Image Processing, 2008, 17(10): 1 940-1 949.

[9] ZHANG K, SONG H, ZHANG L. Active contours driven by local image fitting energy[J]. Pattern Recognition, 2010, 43(4): 1 199-1 206.

[10] LI C, XU C, GUI C,etal. Level set evolution without re-initialization: a new variational formulation[C]//IEEE Computer Society Conference on Computer Vision & Pattern Recognition. San Diego: [s.n.], 2005, 430-436.

[11] LI C, XU C, GUI C,etal. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3 243-3 254.

[12] 何传江, 李梦, 詹毅. 用于图像分割的自适应距离保持水平集演化[J]. 软件学报, 2008, 19(12): 3 161-3 169.

[13] 戚世乐, 王美清. 自适应分割弱边缘的活动轮廓模型[J]. 山东大学学报 (工学版), 2013(6): 17-20.

[14] ZHANG K H, ZHANG L, SONG H H,etal. Active contours with selective local or global segmentation: a new formulation and level set method[J].Image and Vision Computing, 2010(28): 668-676.

(责任编辑： 洪江星)

Adaptive active contour starting with a constant initialization

GUO Yabin，WANG Meiqing

(College of Mathematics and Computer Science，Fuzhou University，Fuzhou，Fujian 350116，China)

Abstract:Level set method, proposed by Li Chunming (LI model), solve the problem of the geodesic active contour model (GAC) which need to reinitialize, but the result of this model with weak edge or uneven gray-level image segmentation is still not ideal. To overcome these problems, a new adaptive active contour model with constant initialization is proposed in the paper. The coefficient of the proposed model contains the mean gray value of the image, so that improve the active contour in the process of evolution of fuzzy boundary identification ability. At the same time, to redefine the external energy to avoid over-segmentation phenomenon. The experimental results show that the effectiveness of the proposed model.

Keywords:image segmentation; active contour; adaptive; weight coefficient

DOI:10.7631/issn.1000-2243.2016.03.0424

文章编号：1000-2243(2016)03-0424-07

收稿日期:2014-05-15

通讯作者:王美清(1967-), 教授，主要从事图像处理方面的研究，mqwang@fzu.edu.cn

基金项目:国家自然科学基金资助项目(11071270)

中图分类号：TP391

文献标识码：A