加权极限学习机的多变量时间序列预测方法

叶秋生, 陈晓云

(福州大学数学与计算机科学学院，福建 福州　350116)

加权极限学习机的多变量时间序列预测方法

叶秋生, 陈晓云

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：提出一种基于样本分布的极限学习机预测模型WELMSD. 该模型先用kN近邻密度估计方法估计出样本的密度值，再用估计出的密度值给传统ELM的经验风险项加权，克服传统ELM在对时间序列进行预测时忽略样本分布的缺点. 基于Rossler混沌时间序列和上证、 深证股票数据的实验仿真结果证明了所提算法的有效性，且当近邻参数kN取值较小时，所提模型对参数不敏感，是一种更优的多变量时间序列预测模型.

关键词：加权极限学习机； 多变量时间序列； 预测； kN近邻密度估计

0引言

时间序列预测技术被广泛应用于金融、 交通、 电力等领域，例如股票涨跌、 交通流量、 电力负荷的预测等. 但是，许多实际时间序列都是非平稳和非线性的，使得传统时间序列预测模型(如AR, ARMA, ARIMA等线性模型)的应用受到极大的限制. 非线性时间序列预测方法能够较好地处理非线性问题，从而得到更深入的研究和更广泛的应用[1].

极限学习机(extreme learning machine, ELM)是Huang等[2]根据广义逆矩阵理论和传统神经网络提出的一种新算法，该算法既保留传统神经网络能够较好地处理非线性问题的优点，又克服传统神经网络需要繁琐迭代的缺点，仅通过一步计算就能求出隐节点的输出权值. 同传统神经网络相比，ELM极大地提高了网络的学习速度和泛化能力，近年来被广泛应用于时间序列的预测并取得良好的预测效果[3]. 但多数ELM时间序列预测方法在训练ELM模型时同等地看待滑动窗口内的样本[4-5]，这显然是不合理的. 实际情况下, 滑动窗口内的样本对预测点的影响是有差异的[6]. 文献[6]认为与预测点时间上较近的样本对预测点的影响较大，赋予较大的权重，而时间上较远的样本对预测点的影响较小，赋予较小的权重. 但是，该思想凭经验而来，缺乏一定的理论支持，预测精度可能会因数据的不同而有较大的差异.

基于以上不足，将传统ELM算法和kN近邻密度估计方法结合起来，提出基于样本分布的加权极限学习机算法(weighted extreme learning machine based on sample distribution, WELMSD). WELMSD算法先通过kN近邻密度估计方法估计出样本的密度值，再用估计出的密度值给传统ELM的经验风险项加权，从而考虑样本点的分布情况，提高了模型的预测性能.

1极限学习机分析

1.1极限学习机(ELM)预测模型[4]

(1)

其中： h(xi)=(g(w1, b1, xi), …, g(wL, bL, xi))为隐含层关于xi的输出向量； L为隐节点的个数； wj为第j个隐节点的输入权值； bj为第j个隐节点的偏差； β为隐含层的输出权值； g(wj, bj, xj)为第j个隐节点的激励函数，可在“Sigmoid”，“Sine”，“RBF”中选择.

根据拉格朗日乘子法和KKT最优条件，得[4]：

(2)

其中

(3)

从而可求得预测模型

(4)

1.2样本分布对传统ELM模型的影响

在机器学习中，通常用期望风险R[f]来评价一个决策函数f(x)的优劣性，期望风险R[f]表达式[7]为：

(5)

其中：P(x,y)为分布函数；c(x,y,f(x))为损失函数.

通常情况下，P(x,y)是未知的，期望风险无法直接计算. 常用下式去逼近期望风险：

(6)

式(6)称为经验风险.

在传统ELM模型中，决策函数为：

(7)

损失函数为：

(8)

经验风险为：

(9)

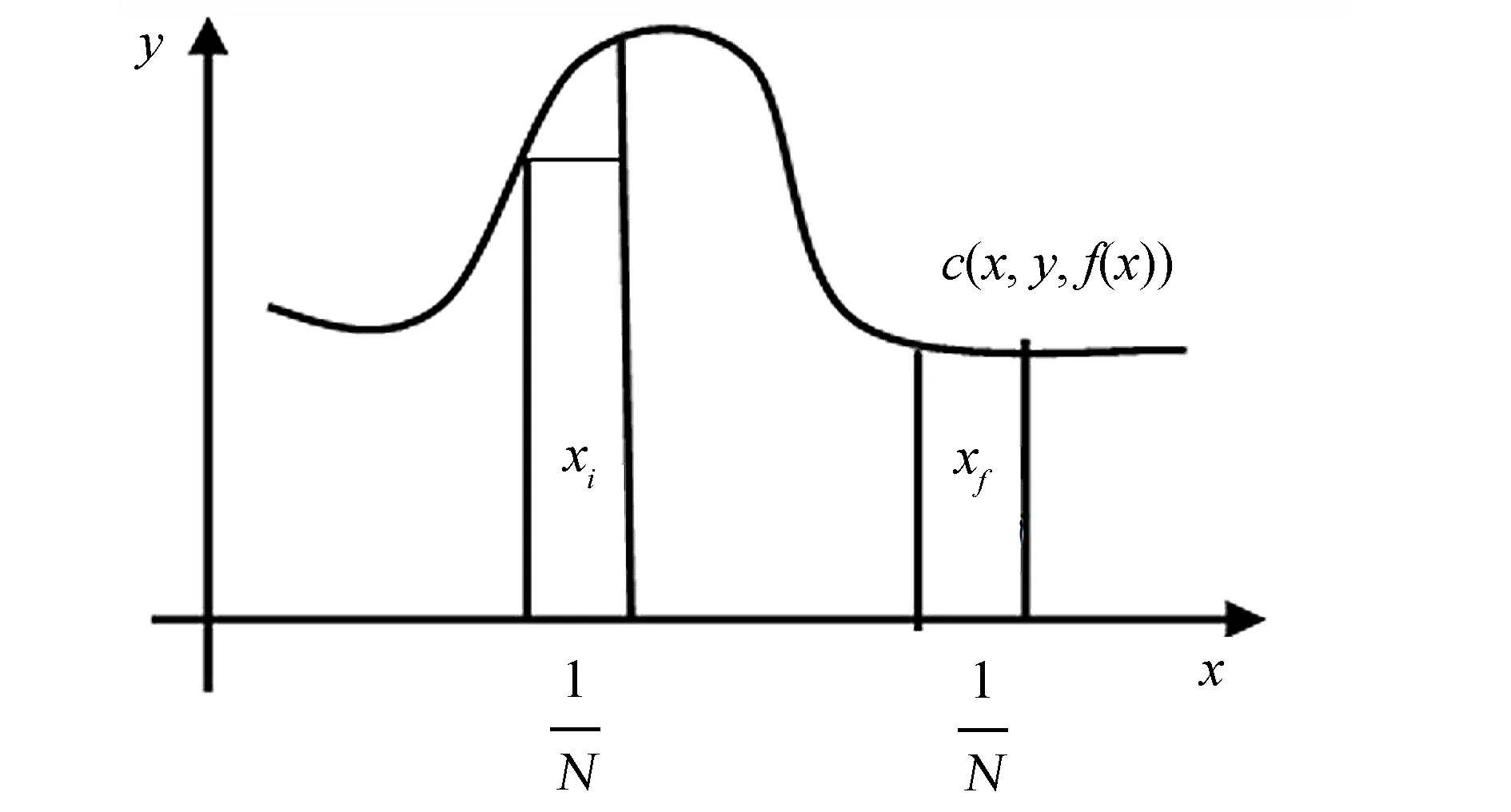
图1　样本分布对ELM的影响Fig.1　The effect of sample distribution on ELM

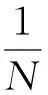
2加权极限学习机的多变量时间序列预测方法

2.1kN近邻密度估计方法[8]

要估计数据集X={x1, …,xN}的概率密度，应先给定近邻样本数kN，再根据要估计密度的样本xi的第kN个近邻与该样本的距离计算出小舱的体积Vi, 则样本xi的概率密度估计值为:

(10)

2.2加权极限学习机的多变量时间序列预测模型

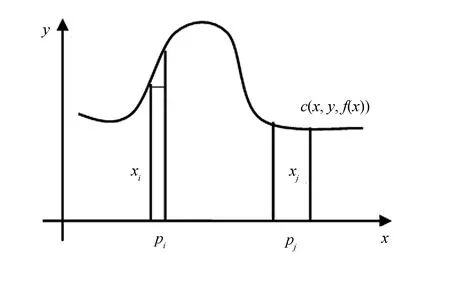
图2　样本概率密度对ELM的影响Fig.2　The effect of Sample probability density on ELM

传统的ELM算法忽略样本概率密度对经验风险项的影响，直接用经验风险去逼近期望风险，这样会使得密度较小的样本的预测值与实际值偏差较大. 为减小小密度样本的预测误差，提出基于样本分布的加权极限学习机算法.

如图2所示，当N<<∞时，在y值分布较为密集(密度值较大)的xj处，小矩形的宽能够适当地放大而不影响小矩形面积对曲线c(x, y, f(x))和坐标轴所围的几何图形面积的逼近. 而在密度较小(密度值较小)的xi处，宽应适当地变小. 基于此，将图1所示的小矩形的宽由1/N修改为pi, 其中，pi(i=1, …, N)为训练样本的密度估计值. 则传统ELM的经验风险项Remp[f]变为

(11)

因此，基于样本分布的加权极限学习机算法的目标函数为：

(12)

式(12)同样可采用拉格朗日乘子法求解：

(13)

其中，αi(i=1, …,N)为拉格朗日乘子. 根据KKT最优条件可解得:

(14)

(15)

(16)

由式(14)、 (15)、 (16)可得

(17)

从而可得预测模型

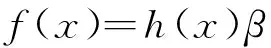
(18)

3实验与结果分析

3.1实验数据

为验证方法的有效性，将其应用到Rossler混沌系统、 上证指数(代码000001)和深证指数(代码399001)时间序列预测中. Rossler映射产生的混沌时间序列方程为：

(19)

其中，a, b和c都是常数. 实验时取a=0.15, b=0.20, c=10.0, x(0)=0.1, y(0)=0.1, z(0)=0.1，步长h=0.01，生成1 000个时间序列数据.

上证指数(代码000001)和深证指数(代码399001)时间序列数据从Yahoo Finance获得. 其中，上证指数的时间跨度为2009年1月5日到2014年2月28日； 深证指数的时间跨度为2010年1月4日到2014年2月28日. 实验时，每个数据集的前2/3作为训练集，后1/3作为测试集. 并将本文WELMSD算法与ELM[4]、 加权极限学习机(weighted extreme learning machine，WELM)(WELM的加权方法同文献[6])以及加权最小二乘支持向量机[6](weighted least squares support vector machines，WLSSVM)进行比较. 为定量比较不同预测方法的预测性能，采用均方根误差(root mean square error，RMSE)作为评价指标：

(20)

实验所用硬件平台：CPU为Pentium(R)Dual-CoreE5300，主频2.60GHz，2GB内存. 软件平台：Matlab7.11.0(R2010b).

3.2实验结果分析

3.2.1各预测方法在不同数据上的RMSE值对比

实验过程中，ELM、WELM以及WELMSD的参数C=1，隐节点个数L=20或L=30[9]，WELMSD的kN近邻数为3； 激励函数g(wj,bj,xi)为“Sigmoid”； WLSSVM的参数C和σ由粒子群优化算法搜索取得. 由于ELM、 WELM和WELMSD隐节点的输入权值w和偏差b都是随机给出，而w和b对实验结果有一定的影响； 粒子群算法有时会陷入局部最优，而局部最优解往往有多个，从而对WLSSVM的预测结果产生影响. 为了更有效地比较各方法的性能，每个方法的RMSE取10次实验结果的平均. 实验采用滑动窗口法去获取训练集的输入、 输出以及测试集的输入、 输出.

滑动窗口具体做法为： 先将滑动窗口置于数据集X的始端，然后逐步向后滑动，每次滑动的时间跨度为1，处于窗口内的数据即为训练集或测试集的输入，而窗口外的后一个数据即为训练集或测试集的输出. 当滑动窗口从数据集X的始端滑到末端时，就会产生N-n个输入和N-n个输出，其中，N为数据集X的样本个数，n为滑动窗口的大小，实验取n=10[10]. 在Rossler混沌时间序列上用变量x,y,z对变量z进行预测，在上证、 深证股票数据上，用开盘指数、 最高指数、 最低指数和收盘指数对收盘指数进行预测. 表1给出了ELM、 WELM、 LSSVM以及WELMSD算法在各数据集上预测的RMSE值的对比.

从表1可以看出，在RMSE指标下，ELM、 WELM以及WELMSD算法在三组数据中的预测精度都随着隐节点个数L的增大而提高，这是因为L变大时，ELM、 WELM以及WELMSD能够更好地拟合时间序列的轨迹. 当然，L并不是越大越好，L过大时，ELM、 WELM以及WELMSD算法将会出现过拟合现象. 在Rossler数据集中，L=20或L=30时，WELM的预测精度都高于ELM的预测精度. 而在深证数据集中，WELM的预测精度却低于ELM算法，这是因为WELM算法认为时间上离预测点较近的点对预测点的影响较大，然而这只是直观上的猜测，并没有理论依据，与预测点时间上较远的点对预测点有大的影响这种情况在实际上也是可能出现的.

表1　各预测方法在Rossler、 上证、 深证时间序列的预测结果对比

图3　Rossler预测结果对比Fig.3　Comparison of prediction results on Rossler

从总体上看，WELMSD算法的预测精度是最高的，并且相对于WELM算法更为稳健，证明在预测时将样本的分布情况考虑进去是合理的.

图3～5直观地展现了各方法的预测值与实际值的对比效果，相对于其他算法，WELMSD在测试数据上的预测曲线能够更好地拟合实际曲线，特别是在z值(Rossler时间序列)或收盘指数(股票时间序列)分布较为稀疏的地方，WELMSD算法的预测曲线与真实曲线拟合得更好，充分说明考虑样本的分布情况能够减小稀疏样本的拟合误差.

图4　上证股票预测结果对比Fig.4　　　　Comparison of prediction results on Shanghai 　　　Component Index

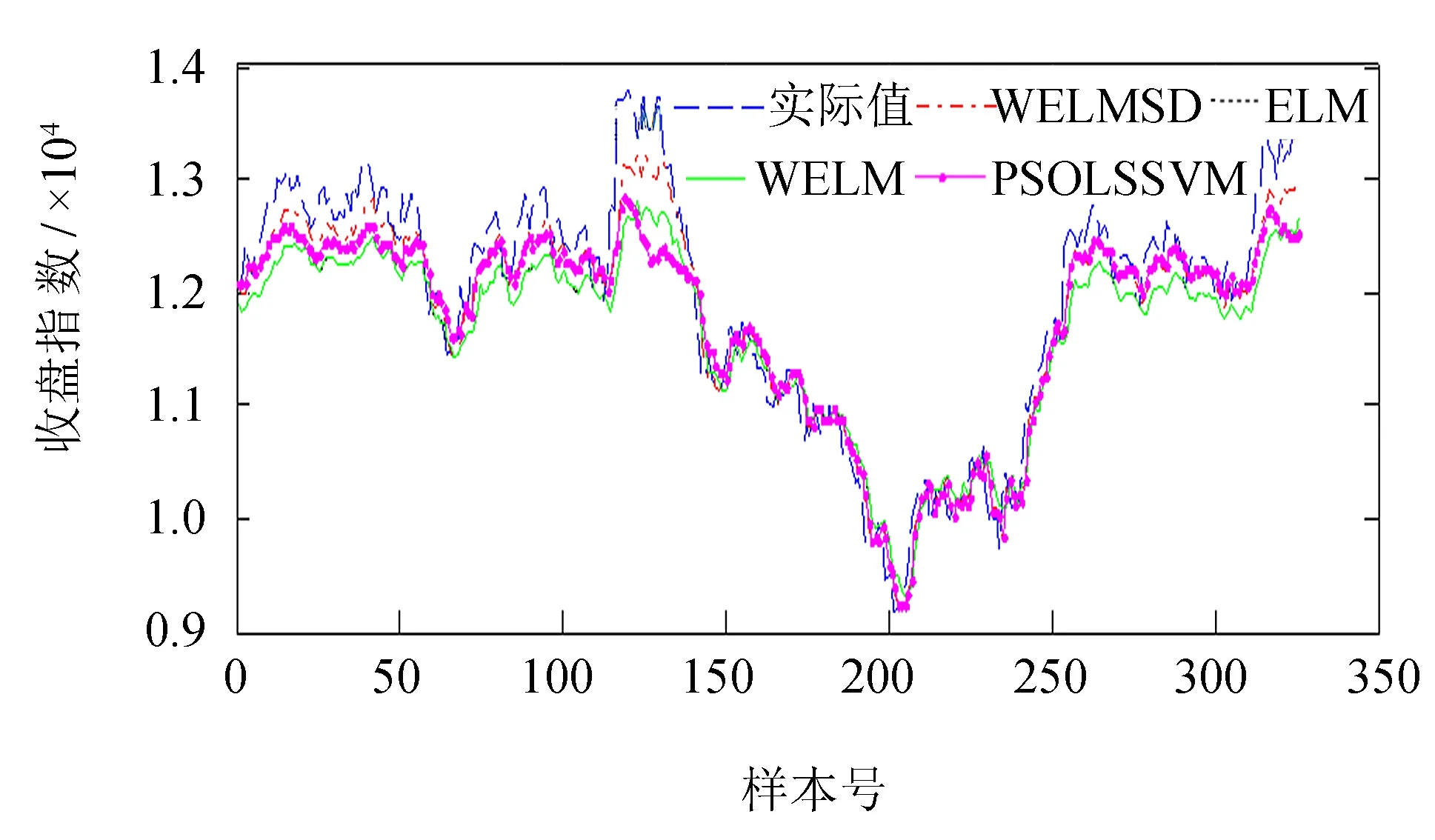
图5　深证股票预测结果对比Fig.5　　　　Comparison of prediction results on Shenzhen　　　 Component Index

3.2.2kN近邻法的参数对预测结果的影响

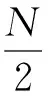
表2　kN对预测结果的影响

4结论

针对多变量时间序列预测问题提出一种基于样本分布的极限学习机预测模型WELMSD，该模型克服了传统ELM忽略样本分布从而导致预测误差较大的缺点. 基于Rossler混沌时间序列和上证、 深证股票数据的实验仿真结果证明了所提算法的有效性，且当kN的取值不超过20时，方法的预测结果对近邻参数kN不敏感，是一种更优的多变量时间序列预测模型.

参考文献：

[1] 江田汉，束炯. 基于LSSVM的混沌时间序列的多步预测[J]. 控制与决策, 2006, 21(1): 77-80.

[2] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1): 489-501.

[3] SINGH R, BALASUNDARAM S. Application of extreme learning machine method for time series analysis[J]. International Journal of Intelligent Technology, 2007, 2(4): 361-367.

[4] HUANG G B, ZHOU H, DING X,etal. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics Part B: Cybernetics, 2012, 42(2): 513-529.

[5] 毛力，王运涛，刘兴阳，等. 基于改进极限学习机的短期电力负荷预测方法[J]. 电力系统保护与控制, 2012, 40(20): 140-144.

[6] GUO Y M, RAN C B, LI X L,etal. Weighted prediction method with multiple time series using multi-kernel least squares support vector regression[J]. Eksploatacja I Niezawodno, 2013, 15(2): 188-194.

[7] 邓乃扬, 田英杰. 数据挖掘中的新方法: 支持向量机[M]. 北京： 科学出版社, 2004.

[8] 张学工. 模式识别 [M]. 3版. 北京： 清华大学出版社, 2010.

[9] ZOMG W, HUANG G B, CHEN Y. Weighted extreme learning machine for imbalance learning[J]. Neurocomputing, 2013, 101(3): 229-242.

[10] GUO Z Q, WANG H Q, LIU Q. Financial time series forecasting using LPP and SVM optimized by PSO[J]. Soft Computing, 2013, 17(5): 805-818.

(责任编辑： 洪江星)

Multivariate time series prediction based on weighted extreme learning machine

YE Qiusheng, CHEN Xiaoyun

(College of Mathematics and Computer Science，Fuzhou University，Fuzhou，Fujian 350116，China)

Abstract:Put forward a kind of extreme learning machine prediction model based on sample distribution which is called WELMSD. WELMSD estimates the density of the sample set by the kN nearest neighbor density estimation firstly, and then weighted for the traditional extreme learning machine by the estimated density. WELMSD overcome the shortcoming of traditional extreme learning machine ignore the sample distribution when it is used for time series prediction. The effectiveness of WELMSD is demonstrated by simulation results on Rossler chaotic time series, Shanghai Composite Index and Shenzhen Component Index. In addition, the prediction results are not sensitive to the parameters of kN nearest neighbor density estimation method when kN is small. It proves that the new model is a better prediction model for multivariate time series.

Keywords:weighted extreme learning machine； multivariate time series； prediction； kN nearest neighbor density estimation

DOI:10.7631/issn.1000-2243.2016.03.0437

文章编号：1000-2243(2016)03-0437-06

收稿日期:2014-03-31

通讯作者:陈晓云(1970-)，教授，主要从事数据挖掘、 模式识别、 机器学习等方面的研究，c_xiaoyun@21cn.com

基金项目：国家自然科学基金资助项目(71273053)； 福建省自然科学基金资助项目(2014J01009)

中图分类号：TP311

文献标识码：A