大型风机的独立变桨控制方法

韩 兵，周腊吾，陈 浩，田 猛，邓宁峰

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南世优电气股份有限公司，湖南 湘潭 411100)

大型风机的独立变桨控制方法

韩 兵1，周腊吾1，陈 浩2，田 猛1，邓宁峰1

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南世优电气股份有限公司，湖南 湘潭 411100)

为了缓解风力发电机组由于风速扰动所造成的疲劳载荷，给出了一种基于 RBF神经网络滑模独立变桨控制策略。通过分析风力机的基本特性，提出将 RBF神经网络滑模功率控制单元和独立变桨控制单元相结合的控制方式。RBF神经网络滑模功率控制单元通过对发电机电磁转矩及桨叶桨距角的控制来平衡风力机的气动转矩，使风轮保持额度转速，实现稳定风电机组的输出功率的目的。而RBF神经网络独立变桨滑模控制单元通过实时微调风机桨距角，来优化功率控制单元的统一桨距角信号，实现缓解风机结构疲劳载荷的目的。最后，通过建立基于 RBF神经网络滑模独立变桨控制的风力发电机组进行相应的仿真与实验，证明基于RBF神经网络功率控制和独立变桨滑模控制相结合的方法具有良好的控制效果，稳定风机输出功率的同时，极大地缓解风机的结构载荷，降低风力发电机组的维护成本。

大型风机；独立变桨控制；径向基向量；俯仰力矩

0 引言

近年来，由于世界能源短缺的矛盾日益尖锐，寻找新的可再生能源资源成为当务之急。风力发电是目前各种再生能源中最成熟的技术，也被广泛的利用的绿色能源之一[1-2]。为满足商用市场的日益发展需求，提高风电机组的单位能源生产成本，风力发电机组的单机容量越来越大。对于大型风机来说，机组捕获更多风能实现最优功率跟踪的同时，必须尽量减小结构的疲劳载荷，优化风电机组的运行方式，这样就对风机的控制策略提出了更高的要求[3]。目前，大型风力发电机组的主要形式为变桨变速风力发电机组，这样可以通过对桨叶的桨距角进行相应的控制，使得风轮转速恒定在额度转速，稳定发电机的输出功率[4-6]。因此，大型风电机组的变桨控制策略的研究已经成为当前研究热点。变桨控制方式按桨距角的类型可以分为统一变桨控制(Collective Pitch Control)和独立变桨控制(Individual Pitch Control)[7-9]。统一变桨控制方式给风机桨叶相同的桨距角信号，而独立变桨距控制方式的桨叶桨距角信号则不相同，以此来平衡风机桨叶的受力不均，实现减小疲劳载荷的目的。

风机变桨控制系统的控制品质受结构或参数的变化影响，使得传统的控制方式在变桨控制系统中存在许多的缺陷。文献[10]通过给出一种寻求风机的最大功率点，以此优化风机变桨控制算法，减少最大功率点附近的桨距角的波动，提高风机输出功率的稳定性。文献[11]利用神经网络控制实时修正风机的Cp-λ特性曲线，建立风机自适应控制模型，根据测量的风速信号调节风轮转速，实现减小风机的疲劳载荷及稳定输出功率。文献[12]引入微分几何的线性化优化方法，设计风机变桨反馈控制系统，但是对于变桨控制系统本身是时变非线性系统，很难精确确定风机变桨系统的模型，当出现风速扰动时，该方法很难保证变桨控制系统的稳定性。文献[13]通过分析风机基本的转矩与桨距角的控制方法，推导出传统PID风机控制结构与相关参数，利用线性二次高斯控制理论来优化风机控制的相关参数，实现风机的最大功率跟踪。文献[14]通过分析风电机组的风速动态相关特性与湍流影响，在风速预测的基础上给出了变桨距风电机组的非线性自适应控制方式，实现了风机的稳定性控制。文献[15]依据风轮旋转过程中的位置进行桨叶方位角的载荷分析，这样风机周期性力矩能很好的通过设计相应的控制策略来抑制不平衡，但这种独立变桨控制策略属于滞后控制，当风速出现大扰动过程，风机无法进行实时控制，出现滞后性的随机载荷，影响风机的运行寿命。

本文为缓解风力发电机组由于风速扰动所造成的疲劳载荷，给出了一种基于RBF神经网络滑模独立变桨控制策略。通过分析风力机的基本特性，提出将RBF神经网络滑模功率控制单元和独立变桨控制单元相结合的控制方式。RBF神经网络滑模功率控制单元通过对发电机电磁转矩及桨叶桨距角的控制来平衡风力机的气动转矩，使风轮保持额度转速，实现稳定风电机组的输出功率的目的；而RBF神经网络独立变桨滑模控制单元通过实时微调风机桨距角，来优化功率控制单元的统一桨距角信号，实现缓解风机结构疲劳载荷的目的。最后，通过建立基于RBF神经网络滑模独立变桨控制的风力发电机组进行相应的仿真与实验，证明基于RBF神经网络滑模功率控制和独立变桨滑模控制相结合的方法具有良好的控制效果，稳定风机输出功率的同时，极大的缓解风机的结构载荷，降低风力发电机组的维护成本。

1 风力机特性

风能的基本转换过程即动能(通过风轮)转换为电能(通过发电机)，其风机的输出功率与有效风速的之间关系为[16]

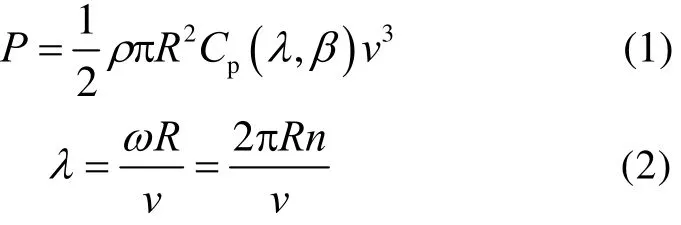
式中：ρ为空气密度；R为风轮半径；ω为风轮角速度；v为风速；β为桨距角；λ为叶尖速比；Cp为风能利用系数。

风能利用系数 Cp是表征风力发电机组吸收转换风能程度的重要参数。在风机实际运行过程中，通过改变 Cp大小以提高或限制风能的能量转换率，达到期望功率的输出。风能利用系数 Cp可以用下面公式近似表示[17]。

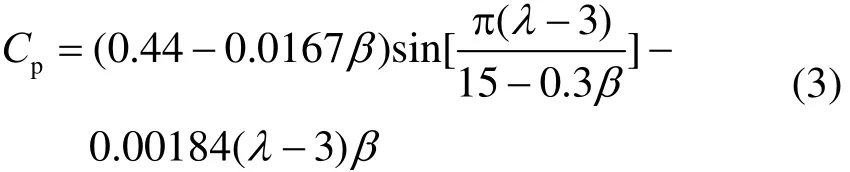
由此可以得到的 Cp-λ特性曲线，如图1 所示。

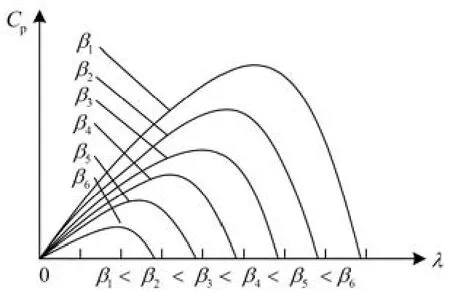
图1 风能利用率 Cp-λ的关系图Fig. 1 Wind energy utilization Cp-λ of diagram

目前大型变速恒频风电机组根据各阶段的参数变化分为三种运行状态，即起动状态、欠功率状态和额定功率状态，如图2所示。

风速达到切入风速后，风机桨叶向0°旋转，气流对叶片产生一定的升力，风轮开始转动，风机进入起动状态。在发电机并网之前，风机桨叶的桨距角给定值由发电机转速信号进行控制，根据给定速度值来调整桨距角的大小，以寻求最佳的并网时机，确保稳定的并网；发电机并网后，风速未达到额定风速，发电机的输出功率在额定值以下，风机进入欠功率状态，目前在此运行状态下风机一直保持最佳桨距角，而欠功率状态根据发电机转速又可分为两个区域：变速运行区和恒速运行区。当发电机转速小于额度转速时，为使风能利用系数Cp始终为最大值，发电机转速的变化随着风速的大小进行相应的改变，实现最大功率追踪控制。

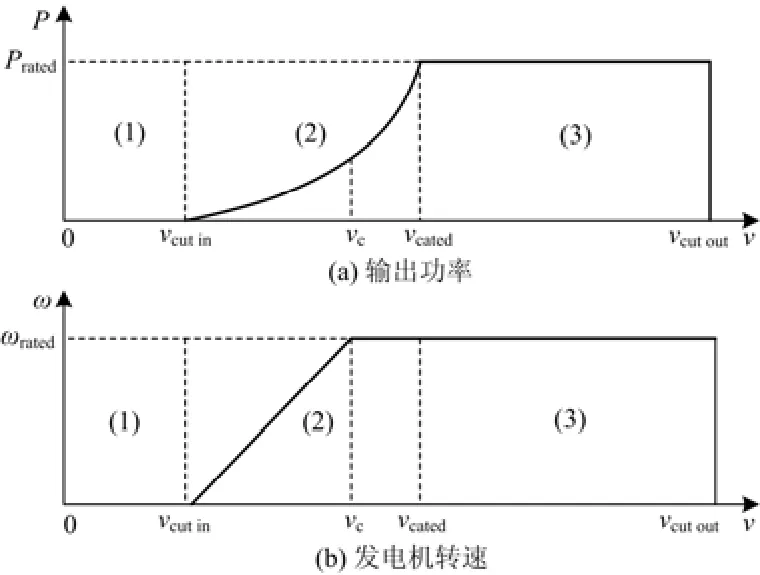
图2 风力发电机组三种运行状态的参数变化图Fig. 2 Parameters of three wind turbines operating status

当发电机转速超过额度转速时，风机进入恒速运行区，在这个运行区域内，为了保护风电机组的安全，通过控制发电机电磁转矩去平衡风机的气动转矩，将发电机转速保持到额度转速上；当风速达到或者超过额定风速后，气动转矩已经无法通过发电机电磁转矩去平衡，所以在发电机电磁转矩的输出能力和风轮转速的双重限制下，必须通过变桨控制系统改变桨距角来限制风轮捕获的能量，使风电机组的输出功率维持在额定功率附近，风机进入额定功率状态，而在此状态下进行风电机组的独立变桨控制是本文研究重点。

2 基于 RBF 神经网络滑模控制

RBF 神经网络滑模控制是依据风力发电机组控制系统的运行状态来调节功率控制与独立变桨控制器的参数，最终实现风机控制系统的最优化。就大型风机来说，当风电机组进入额度功率状态，风机的控制系统采用功率控制与独立变桨控制相结合的方式，协调桨距角的同时稳定风轮转速，考虑风力发电机组的控制系统为高度的时变非线性系统[18]，假设如下。

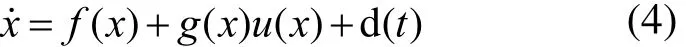
式中：x=[x1, x2, …, xn]为风机控制系统的可测状态变量； )(xu 为控制系统输入变量； )(xf 和 )(xg 为控制系统有界未知的连续函数；d(t)为风速干扰。

本文的控制目标一是稳定风机的输出功率，所以将风轮转速设为恒定值；二是缓解风机疲劳载荷，所有的将桨叶桨距角的反馈误差作为输入变量。故本文采用的 RBF 神经网络滑模控制将风轮转速作为跟踪对象，取风轮转速反馈得出状态误差及其导数，这样选取的控制系统滑模平面为[19]

为了实现对风电机组RBF神经网络滑模独立变桨控制，本文建立简化风机线性化模型的状态方程如下所示[20]。

式中：rW为风轮转速；J为风机的转动惯量； Mr为风轮的转矩；H为风机中心的高度；S为风机塔基刚度；M 为风轮总质量；ψi为风轮方位角；snay为机舱左右扰度；snod为机舱俯仰扰度；D 为风机的阻尼系数；vi为风轮平面的测量风速；θi为风机的桨距角；Myaw为风机偏航力矩；Mpitch为风机俯仰力矩；Fax为机舱的轴向力；Fsd为机舱的侧向力；hFx为桨叶俯仰力与风速的导数；hMz为桨叶俯仰力矩与风速的导数；kMx为气动力矩与桨距角的导数；hMx为气动力矩与风速的导数；kFx为桨叶拍打力与桨距角的导数；kMz为桨叶拍打力矩对桨距角的导数。

本文建立的基于 RBF 神经网络的滑模变结构控制的独立变桨距控制系统原理图如图3所示。其中 RBF 神经网络滑模功率控制单元，通过采集风轮转速信号，风力机功率控制系统根据风轮转速rW和额度风轮转速ratW 的比较，计算得到风机桨叶的统一桨距角 θ 和风轮转矩 Tgset。而 RBF 神经网络的滑模独立变桨距控制则采集叶根弯矩信号 Mz1、Mz2、Mz3，之后通过科勒曼(Coleman)坐标轴变换，将旋转平面坐标轴转化为固定平面坐标轴，得到桨叶的俯仰力矩 Mpitch和偏航力矩 Myaw，将俯仰力矩和偏航力矩进行 Coleman 逆变换转换成旋转平面上的三个微调桨距角 θicm，最后将微调桨距角 θicm和功率单元计算得来的统一桨距角θ相加，得到风机三个桨叶的各自桨距角 θi，变桨伺服器再根据相应的信号进行独立变桨控制。

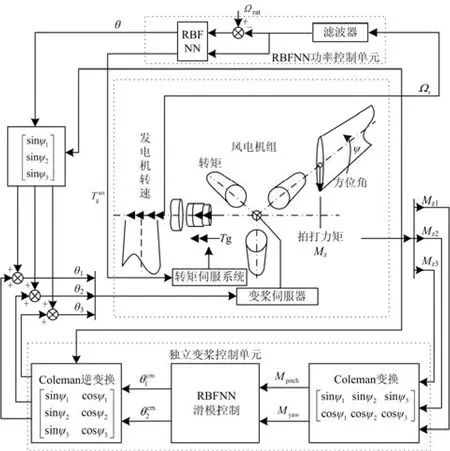
图3 基于 RBFNN 滑模独立变桨控制系统原理图Fig. 3 Schematic diagram of system based on RBFNN sliding individual pitch control

独立变桨控制单元中风电机组的叶根弯矩信号Mz1、Mz2、Mz3，通过科勒曼坐标变化为固定坐标轴下的俯仰力矩和偏航力矩，具体如式(6)所示。

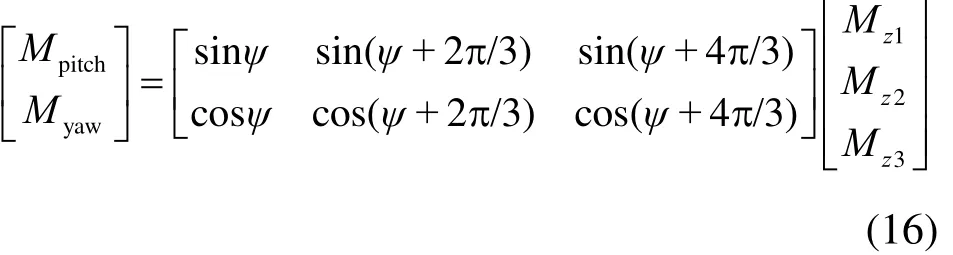
Coleman 逆变换转换成旋转平面上的三个微调桨距角 θi，如式(7)所示。

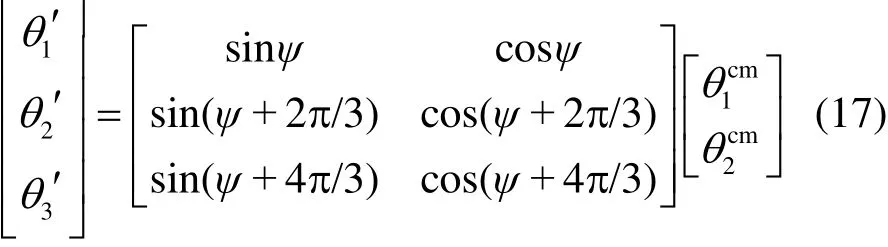
文中的独立变桨控制单元通过在 RBFNN 中引入等效滑模控制的作用来优化系统控制结构，使系统按照预定的轨迹运行，最终将会收敛于本文设计的滑模面[21]，改善由于风速扰动造成的桨叶拍打振动，缓解风机疲劳载荷。控制系统存在正负常数使系统稳定在相应区间，如下：

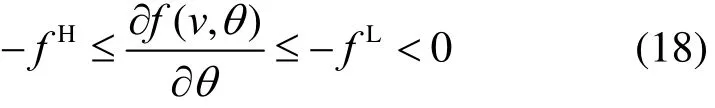
式中，fH、fL分别为独立变桨控制系统的连续函数的上界和下界。

RBF神经网络滑模控制系统结构如图4所示，设 RNFNN 的径向基向量 h=[h1,h2,…,hm]T，则控制系统高斯函数 hj，如式(19)[22]。

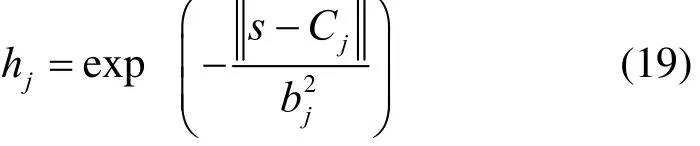
式中：cj=[c11,c12,…, c1m]；b=[b1,b2,…, bm]。

图4 基于 RBFNN 滑模控制结构图Fig. 4 Structure chart of RBFNN sliding-mode control

而 RBFNN 滑模控制系统的输出变量为

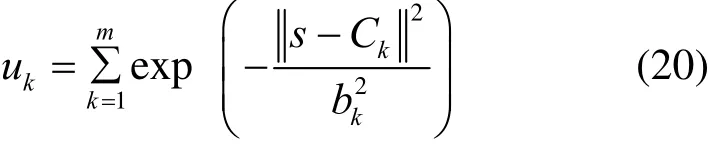
式中，m为神经网络隐含层的节点数目。根据式(18)，计算得到：

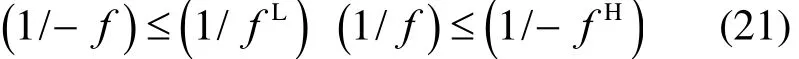
根据 Lyapunov 的稳定性原理，如下：

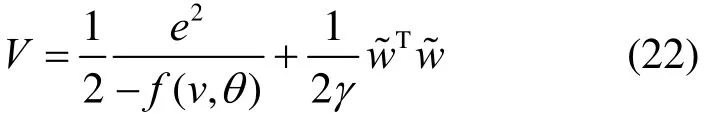
式中，γ为 RBFNN 的自适应参数。

对式(22)的 Lyapunov 方程进行求导计算，得到：

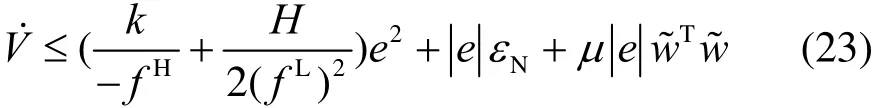
这样 RBFNN 滑模独立变桨控制系统沿着滑模面向着系统减小的方向调整，最终使系统趋于稳定。

3 仿真分析

本研究利用 2 MW 风电机组为仿真测试机组，风力发电机组的主要参数如表1所示。

表1 2 MW 风力发电机组主要参数表Table 1 2 MW wind turbine parameter list

湍流平均风速为 14 m/s，风剪切系数为 0.2，湍流强度为 3.7%的情况下，利用 MATLAB 和 GH Bladed 联合建立风机模型，图5 为在风剪切、塔影效应和湍流影响下，风机桨叶叶尖处的风速情况，可见桨叶1的叶尖处的风速在该叶片旋转到风轮平面在 5º左右时达到风速波动的最大点，旋转到 180º左右时达到最低点，桨叶2和3达到极值风速的位置分别延后 120º，如图5 所示。

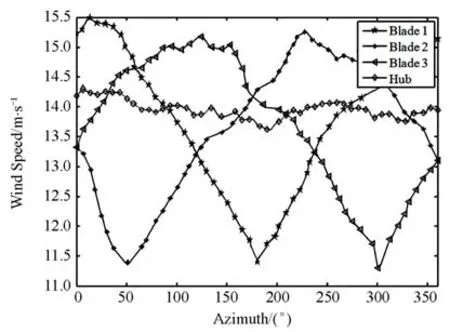
图5 风剪切、塔影和湍流影响下叶尖处风速模型Fig. 5 Wind speed at the tip affected by wind shear, tower shadow and turbulence

在不考虑任何影响因素情况下，风机桨叶1在旋转平面内受力平衡，其摆振力矩和挥舞力矩是稳定值，从图6(a)和图6(b)可见，当风机受风剪切影响时，桨叶1的挥舞力矩和摆振力矩在风轮旋转到平面的 180º位置时最小，在叶片旋转到达 0º时达到最大值 4.1×105N·m。当受到塔影影响时，桨叶 1 进入风机的塔影区域 120º~180º的位置，风速将会减小，这样桨叶1的挥舞力矩和摆振力矩也会降低。当风剪切和塔影效应共同影响风机时，桨叶1挥舞力矩和摆振力矩的波动引起的风机波动是这两者之和。当风剪切、塔影效应和湍流共同影响风机时，桨叶1的力矩波动与湍流风速的波动相关，桨叶1挥舞力矩和摆振力矩的变化跟风剪切和塔影效应影响下的风速变化相关，其桨叶1力矩波动的极小值出现在风轮平面的 190°附近。

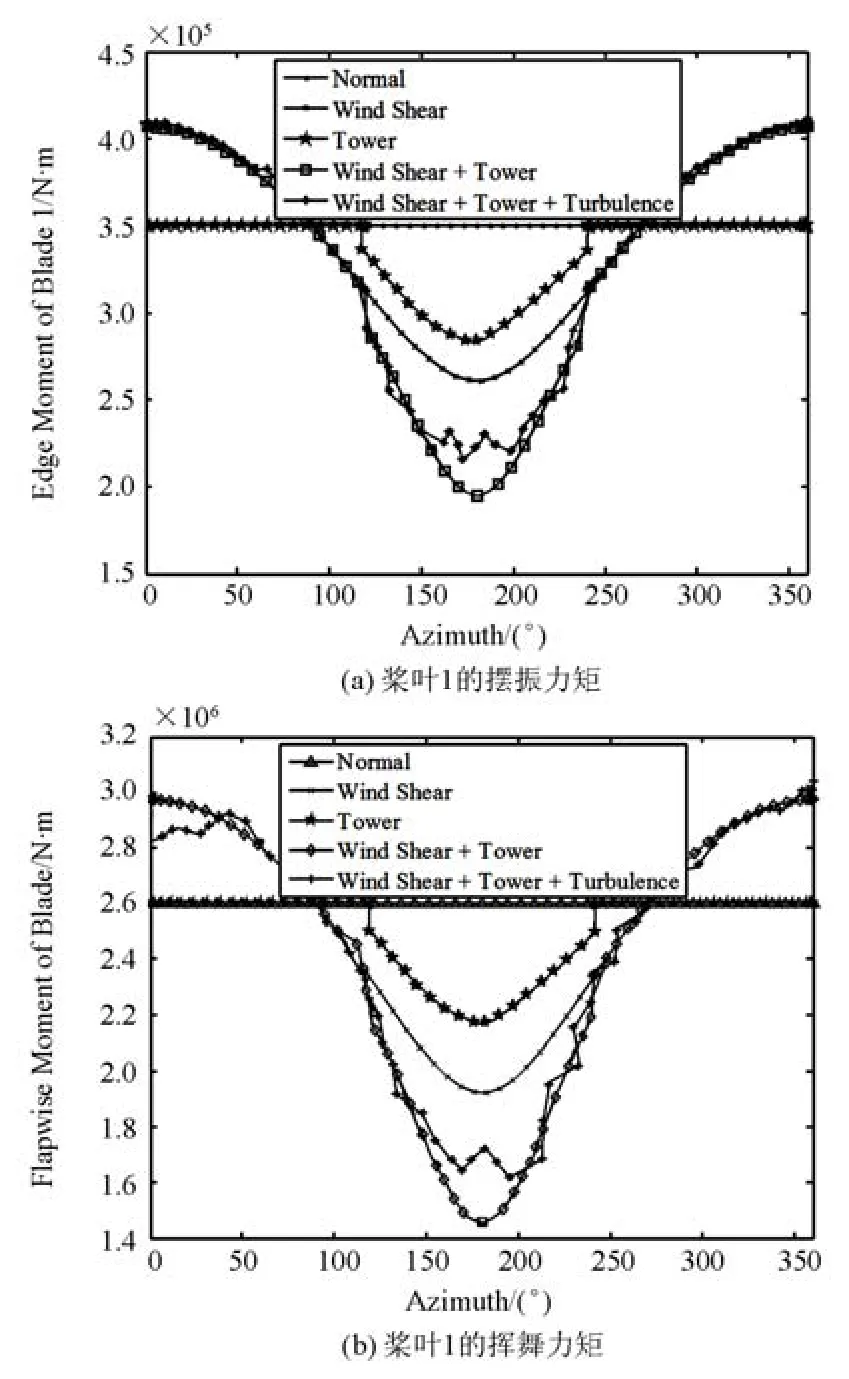
图6 风剪切、塔影和湍流影响下桨叶的力矩波动Fig. 6 Torque ripple blade affected by wind shear, tower shadow and turbulence tower shadow and turbulence

4 实验研究

本研究的风电机组控制系统实验平台，主要由PC上位机模拟风机模型、变桨控制系统和模拟风速对风轮载荷模拟系统等单元构成。基于RBFNN滑模独立变桨控制参数如下所示：c=5，η=0.1，其中高斯函数参数ci=[-2.0 -1.0 0 1.0 2.0]和bi=[-2.0 -1.0 0 1.0 2.0]，RBFNN的起始权值为0.10。本研究采用的湍流平均风速为16 m/s，如图7所示。

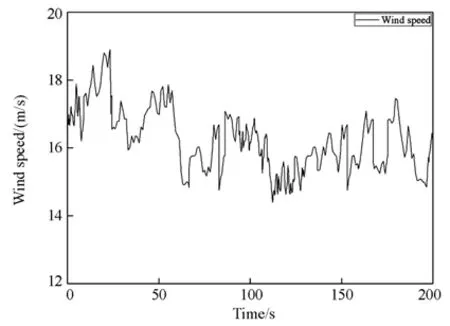
图7 实验的湍流风速Fig. 7 Experimental turbulence wind speed

实验结果如图8中，可以发现采用RBFNN滑模独立变桨的控制方式与传统的统一变桨控制(CPC)比较，可以显著减小由于风速扰动造成的桨叶根部弯矩。基于RBFNN滑模独立变桨后桨叶挥舞力矩峰值较统一变桨控制减少了85.1 kN·m，平均挥舞力矩较统一变桨控制降低约9.3%，这就导致风电机组机舱顶部的俯仰力矩及偏航力矩明显降低，提高风机的可靠性和延长使用寿命。

对桨叶的挥舞力矩进行快速傅里叶(FFT)变换，结果如图9(a)、图9(b)所示，可以从图中发现，采用RBFNN滑模独立变桨控制方式后，风机振动频率的频谱出现明显降低，如风轮旋转频率(即1P)0.28 Hz处，频率频谱峰值较CPC减小了37.9%，这样就是通过独立变桨控制，可以降低风电机组的波动载荷激励力矩，从而实现减小风机振动的效果，降低风力发电机组的维护成本。

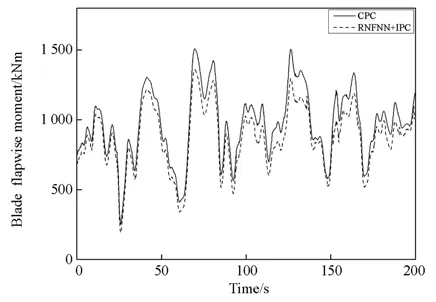
图8 桨叶挥舞力矩对比图Fig. 8 Blade flapwise moment contrast figure

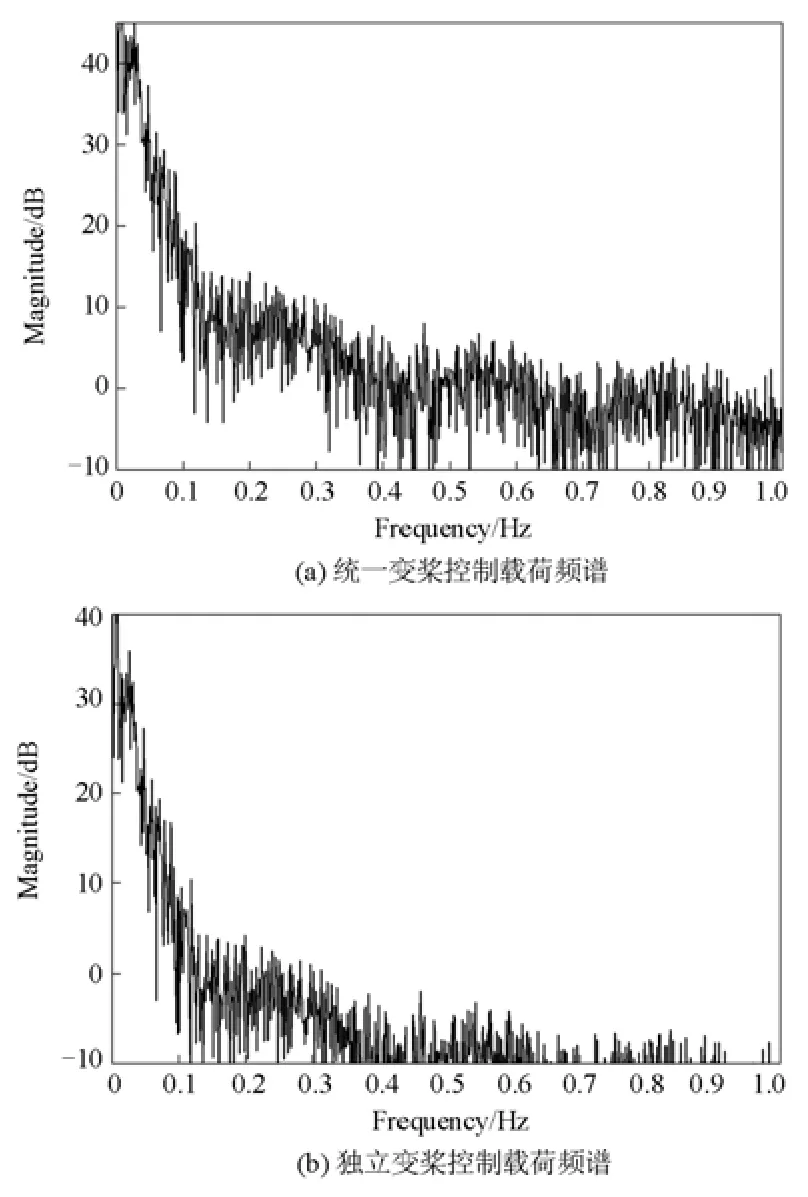
图9 桨叶挥舞力矩载荷频谱对比图Fig. 9 Blade flapwise moment of spectrum

图10 (a)、图10(b)为两种控制方式下风机桨距角的变化曲线，基于 RBFNN 滑模独立变桨控制方式后风机塔基的俯仰力矩波动得到了显著降低，这样对大型风机的基础结构强度要求更低，也就是说，基于RBFNN滑模独立变桨相比传统风机的CPC控制更加适合在大型风电机组上应用。但是桨距角曲线中显示变桨电机会出现周期性的变化，这样会频繁启动变桨电机，对变桨电机的参数要求更加严格。

5 结论

本文为缓解风力发电机组由于风速扰动所造成的疲劳载荷，给出了一种基于 RBF神经网络滑模独立变桨控制策略。通过分析风力机的动态运行特性，提出将 RBF 神经网络滑模功率控制单元和独立变桨控制单元相结合的控制方式。首先RBF神经网络滑模功率控制单元通过对发电机电磁转矩及桨叶桨距角的控制来平衡风力机的气动转矩，使风轮保持额度转速，实现稳定风电机组的输出功率的目的；而 RBF 神经网络独立变桨滑模控制单元通过在线实时微调桨叶桨距角，来优化功率控制单元的统一桨距角信号，实现缓解风机结构疲劳载荷的目的。最后，通过建立了基于RBF神经网络滑模独立变桨控制的风力发电机组进行相应的仿真与实验，证明基于 RBF 神经网络功率控制和独立变桨滑模控制相结合的方法具有良好的控制效果，稳定风机输出功率的同时，极大的缓解风机的结构载荷，降低风力发电机组的维护成本。

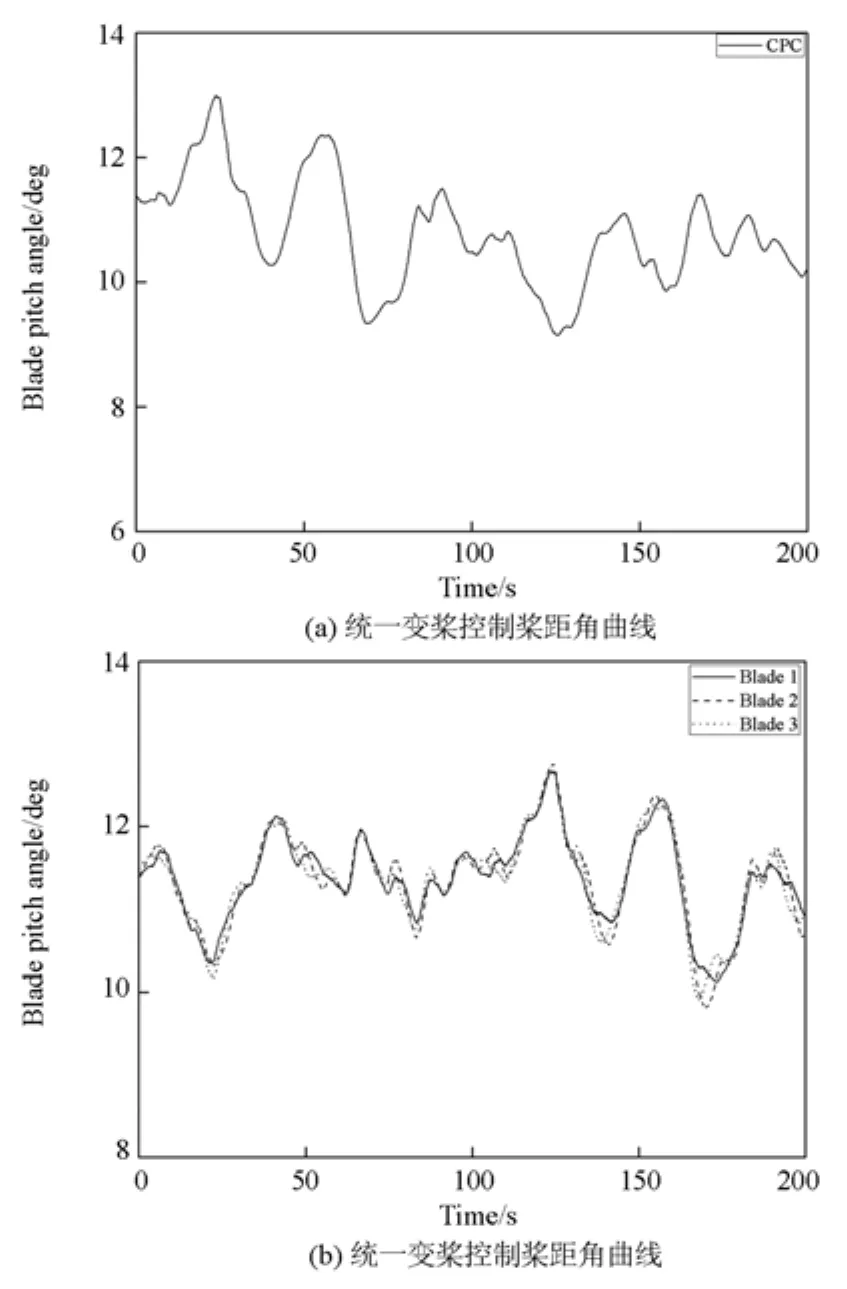
图10 变桨控制桨距角变化对比曲线图Fig. 10 Blade pitch angle change curve

[1]刘波, 金昊. 永磁直驱风电系统双 PWM 变换器前馈补 偿 控 制 [J]. 电 力 系 统 保 护 与 控 制 , 2014, 42(15): 52-57. LIU Bo, JIN Hao. Feed forward compensation control of dual PWM converter for permanent magnet direct driven wind turbine[J]. Power System Protection and Control, 2014, 42(15): 52-57.

[2]张祥宇, 付媛, 王毅, 等. 含虚拟惯性与阻尼控制的变速风电机组综合 PSS 控制器[J]. 电工技术学报, 2015, 30(1): 159-169. ZHANG Xiangyu, FU Yuan, WANG Yi, et al. Control strategy research of low voltage ride through based on the improved wind turbine generator system[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 159-169.

[3]崔双喜, 王维庆, 张强. 风力发电机组独立变桨鲁棒自 适 应 桨 距 角 跟 踪 控 制 [J]. 电 力 系 统 保 护 与 控 制 , 2015, 43(6): 52-57. CUI Shuangxi, WANG Weiqing, ZHANG Qiang. Robust adaptive blade pitch angle tracking control for wind turbines[J]. Power System Protection and Control, 2015, 43(6): 52-57.

[4]周志超, 王成山, 郭力, 等. 变速变桨距风电机组的全风速限功率优化控制[J]. 中国电机工程学报, 2015, 35(8): 1837-1844. ZHOU Zhichao, WANG Chengshan, GUO Li, et al. Output power curtailment control of variable-speed variable-pitch wind turbine generator at all wind speed regions[J]. Proceedings of the CSEE, 2015, 35(8): 1837-1844.

[5]MILLER A, MULJADI E, ZINGER D S. A variable speed wind turbine power control[J]. IEEE Transactions on Energy Conversion, 1997, 12(2): 181-186.

[6]MASIALA M, VAFAKHAH B, SALMON J, et al. Fuzzy selftuning speed control of an indirect field-oriented control induction motor drive[J]. IEEE Transactions on Industry Applications, 2008, 44(6): 1732-1740.

[7]邢作霞, 陈雷, 孙宏利, 等. 独立变桨距控制策略研究[J]. 中国电机工程学报, 2011, 31(26): 131-138. XING Zuoxia, CHEN Lei, SUN Hongli, et al. Strategy study of individual pitch control[J]. Proceedings of the CSEE, 2011, 31(26): 131-138.

[8]米增强, 刘力卿, 余洋, 等. 限电弃风工况下双馈风电机组有功及调频控制 策 略[J]. 电 工 技 术 学 报, 2015, 30(15): 81-88. MI Zengqiang, LIU Liqing, YU Yang, et al. The control strategy of active power and frequency regulation of dfig under wind abandon condition[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 81-88.

[9]GOMIS B O, JUNYENT F A, SUMPER A, et al. Control of a wind farm based on synchronous generators with a central HVDC-VSC converter[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1632-1640.

[10]HOMAIFAR A, MCCORMICK E. Simultaneous design of membership functions and rule sets for fuzzy controllers using genetic algorithms[J]. IEEE Transactions on Fuzzy Systems, 1995, 3(2): 129-139.

[11]TELEKE S, BARAN M E, HUANG A Q, et al. Control strategies for battery energy storage for wind farm dispatching[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 725-732.

[12]HISKENS I. Dynamics of type-3 wind turbine generator models[J]. IEEE Transactions on Power Systems, 2012, 27(1): 465-474.

[13]SELVAM K, KANEV S, WINGERDEN J W, et al. Feedback feedforward individual pitch control for wind turbine load reduction[J]. International Journal of Robust and Nonlinear Control, 2009, 196(12): 72-91.

[14]STEFFEN R, DAVID S, FRANK S. Nonlinear model predictive control of floating wind turbines with individual pitch control[C]// American Control Conference, 2014, 6: 4434-4439.

[15]BOSSANYI E. Further load reductions with individual pitch control[J]. Wind Energy, 2005, 8(4): 481-485.

[16]WANG Q, CHANG L. An intelligent maximum power extraction algorithm for inverter-based variable speed wind turbine systems[J]. IEEE Transactions on Power Electronics, 2004, 19(5): 1242-1249.

[17]DAHAN J A, MORGANS A S, LARDEAU S. Feedback control for form-drag reduction on a bluff body with a blunt trailing edge[J]. Journal of Fluid Mechanics, 2012, 704: 360-387.

[18]窦真兰, 施刚, 曹云峰, 等. 减少风力机转矩波动的异步变桨控制[J]. 电工技术学报, 2014, 29(1): 236-245. DOU Zhenlan, SHI Gang, CAO Yunfeng, et al. Research on individual pitch control for reducing wind turbine torque fluctuation[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 236-245.

[19]JAUCH C, CRONIN T, SORENSEN P, et al. A fuzzy logic pitch angle controller for power system stabilization[J]. Wind Energy, 2007, 10(1): 10-39.

[20]HAMIDREZA J, JEFF P, JULIAN E. Adaptive control of a variable-speed variable-pitch wind turbine using radialbasis function neural network[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2264-2272.

[21]秦斌, 周浩, 杜康, 等. 基于 RBF 网络的风电机组变桨距滑模控制[J]. 电工技术学报, 2013, 28(5): 37-41. QIN Bin, ZHOU Hao, DU Kang, et al. Sliding mode control of pitch angle based on RBF neural-network[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 37-41.

[22]马斌, 张丽艳. 一种基于径向基神经网络的短期风电功率直接预测方法[J]. 电力系统保护与控制, 2015, 43(19): 78-82. MA Bin, ZHANG Liyan. Short-term wind power direct forecasting based on RBF neural network[J]. Power System Protection and Control, 2015, 43(19): 78-82.

(编辑 张爱琴)

Methods of individual pitch control for large wind turbine

HAN Bing1, ZHOU Lawu1, CHEN Hao2, TIAN Meng1, DENG Ningfeng1
(1. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China; 2. Hunan Shiyou Electric Co., Ltd., Xiangtan 411100, China)

In order to alleviate fatigue loads for wind turbines due to wind speed disturbances, this paper presents a sliding individual pitch control strategy based on RBF neural network. By analyzing the basic characteristics of the wind turbine, it proposes a control mode combining with RBF neural network sliding mode power control unit and individual pitch control unit. RBF neural network sliding mode power control unit balances the wind rotor via a pneumatic torque control of the generator electromagnetic torque and blade pitch angle, and keeps the amount of speed to achieve the purpose of stable output power wind turbines. RBF neural sliding network individual pitch control unit optimizes unified unit angle signal of power control through fine-tune real pitch angle, and achieves the purpose of relieving structure fatigue loads for wind turbine. Finally, corresponding simulation and experiments based on RBF neural network independent sliding pitch controlled wind turbines are established, it verifies that the proposed method has good control effect, achieves stability output power for large wind turbine, greatly eases structural loads , and reduces the maintenance costs of wind turbines.

large wind turbine; individual pitch control; radial basis vector; pitch moment

TM614

1674-3415(2016)02-0001-08

2015-03-20；

2015-05-05

韩 兵(1986-)，男，博士研究生，研究方向为大型风力发电系统及其控制与新能源发电技术；E-mail: hanbing 9107@qq.com

周腊吾(1965-)，男，教授，博士生导师，主要研究方向为新能源发电技术、电力电子技术在电力系统中的应用与现代交流调速技术；E-mail: 120116559@qq.com

陈 浩(1976-)，男，硕士，高级工程师，研究方向为风力发电系统及其控制。E-mail: 8646792515@qq.com

国家国际科技合作专项(2011DFA62890)