含分布式电源的配电网双层扩展规划

张彼德，何 頔，张 强，邓 钧，龙 杰

(西华大学电气信息学院，四川 成都 610039)

含分布式电源的配电网双层扩展规划

张彼德，何 頔，张 强，邓 钧，龙 杰

(西华大学电气信息学院，四川 成都 610039)

考虑分布式电源对配电网网架结构的影响，在分布式电源容量和位置均未定的情况下，采用内外层双层规划的方法对配电网线路结构、分布式电源位置和容量进行综合优化。将政府补贴政策引入目标函数，鼓励清洁能源的使用，建立节省综合经济成本最多的目标函数模型。内层在引进分布式电源位置和容量的情况下，在遗传算法中引进组织膜计算中的交流规则来增强全局寻优能力和计算能力，从而实现对网架结构的扩展规划；外层采用新型混合粒子群算法对分布式电源的位置和容量进行确定。算例表明，该算法应用于含分布式电源的配电网扩展规划中，节约了经济成本，提高了用电可靠性，验证了算法的有效性。

分布式电源；配电网；扩展规划；遗传组织膜；新型混合粒子群

0 引言

配电扩展规划是指在满足负荷增长和网络现状的情况下，对线路、变电站等进行优化，满足用户供 电 质 量 和 可 靠 性 的 要 求[1]。 随 着 分 布 式 电 源(Distribute Generation，简称 DG)渗透率的提高，在进行配电网扩展规划时，不得不考虑分布式电源的位置和容量对网架结构的影响[2-3]。

近年来，含DG的配电网规划研究成为热点。文献[4]采用多岛遗传算法对 DG 位置和容量进行规划，建立多目标函数模型，但没有考虑DG对线路扩展的影响。文献[5]模拟分布式风电源出力，采用单亲遗传算法对含风电源的配网网架进行规划，没有考虑 DG 与网架间的相互影响。文献[6]对含 DG配电网进行多目标扩展优化，考虑了三级负荷水平，加入额外的约束条件进行优化，但没有考虑政府的影响。文献[7]建立了含分布式电源与充电站的配电网协调规划模型，但没有对分布式电源的位置进行优化。文献[8]提出在主动配电网模式下，分布式电源接入的优化规划方案，但没有考虑网架结构的扩展规划。因此考虑线路、DG 的位置与容量之间的相互影响，规划出一个合理综合的优化方案很有必要。

针对以上情况，本文以节省最多经济成本为目标，对含DG的配电网进行双层扩展规划。内层运用遗传组织膜算法对含DG配电网的网架进行扩展优化；外层则用新型混合粒子群算法对DG的位置和容量进行调整，调整后的DG再反馈给内层影响网架优化。通过内外两种算法规划出电网线路、DG位置和容量的综合优化方案。

1 含分布式电源的配电网扩展规划数学模型

1.1 目标函数

建立以节省线路新建费用、网损费用、购电成本、停电损失费用、DG 安装费用和发电成本综合成本最多的经济目标函数模型，其数学表达式为

式中：F为总共节省的经济成本；1F为减少的线路新建费用；2F为减少的网损费用；3F为节约的购电成本；4F 为DG折算的年安装成本；5F 为DG的发电成本；6F为减少的停电损失费用。

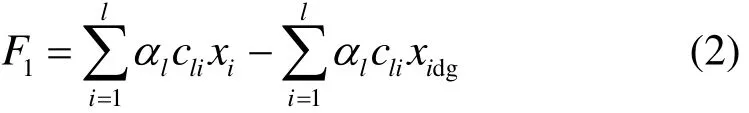
式中：l为可选支路数；la为线路固定投资年平均费用系数；lic 为该支路的新建费用；ix 为不含 DG规划时线路的决策变量；dgix 为含 DG 规划时线路的决策变量。

式中： DPloss为不含 DG 与含 DG 规划的网损之差；Tmax为系统最大负荷年利用小时数； Ce为系统单位电价(kWh)。

式中：lP 为不含 DG 时的网损；dglP 为含 DG 时的网损。

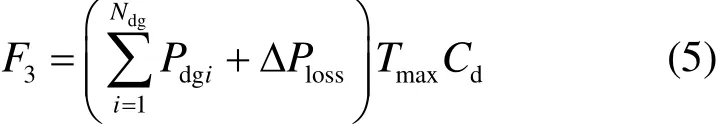
式中：dgN 为 DG 的个数；dgiP 为第 i 个分布式电源的容量；dC 为发电公司单位电价(kWh)。

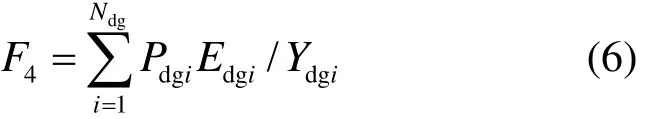
式中：dgiE 为 DG 单位容量安装成本；dgiY 为 DG 的寿命。

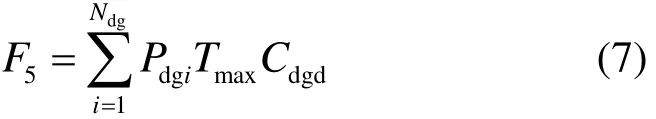
式中，dgdC 为 DG 单位容量发电成本。

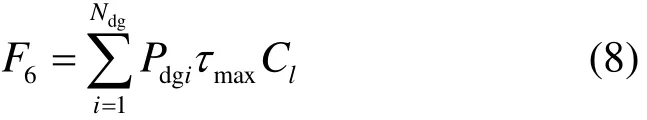
1.2 约束条件

(1) 电压约束

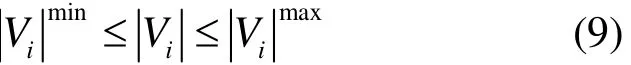
分别为电压的上、下限。(2) 电流约束

(3) 连通性约束

连通性约束是为了保证每个负荷均能被供电。

(4) 辐射性约束

(5) 容量约束

式中：På新增为系统新增负荷总功率；h为 DG 的渗透率，不超过 10%。

2 基于遗传组织膜和动态惯性粒子群算法的含分布式电源的配电网网架扩展规划

本文以获取最多经济效益为目标函数，采用两种算法对含DG的配电网进行双层规划。内层将组织膜计算中的交流规则引入遗传算法中，使所有遗传算子都在膜区域中进行，通过单细胞中膜与膜、单细胞与单细胞、单细胞与中心细胞之间的交流来选择最优的个体，运用此方法来规划含DG的配电网的新建线路。外层对基本粒子群算法进行一定的改进，使其惯性权重和学习因子动态变化，采用交叉策略增加种群多样性，利用变异或混沌扰动操作帮助粒子跳出局部最优[9]，以此来更新优化 DG 位置和容量。将外层优化后的DG再反馈到内层规划中进行网架结构的优化，如此循环直到满足外层终止条件，得到线路结构、DG 位置和容量的综合优化方案。

2.1 遗传组织膜算法的实现

膜计算是模拟生物细胞的机理[10]。组织膜算法属于膜计算中的一种，与细胞膜算法不同的是组织膜计算中的交流规则更加复杂，而且计算能力更强。遗传算法[11-12]具有较强的全局搜索能力，减少陷入局部最优的可能性。结合二者的优点，将遗传算子操作在细胞膜的区域中进行，通过膜间复杂的交流规则形成中心细胞中较好的种群，最后在中心细胞中寻找到最优解。

(1) 遗传算子

所有的遗传算子均是在细胞膜区间中进行的。选择操作采用轮盘赌注法，适应度值好的个体被选择的概率越高，交叉操作采用两点区间交叉，变异操作为单点变异，而且变异概率值很小。

(2) 交流规则

a.单细胞中膜与膜的交流

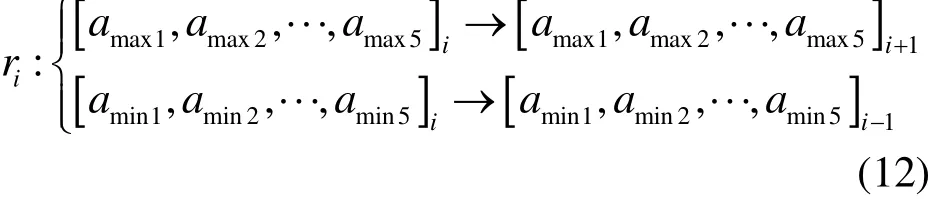
式中：maxa 为单细胞第 i层膜中较好的个体；mina 为第i层膜中较差的个体；本文选取 5个较好、较差的个体进行交流，将较好的个体交换到单细胞的最外层膜中。

b.单细胞与单细胞的交流

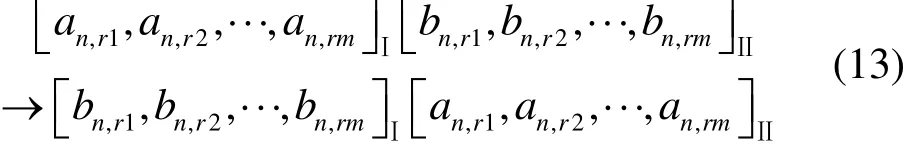
式中：n为每个单细胞的最外层膜，即最好个体层；an,r为单细胞Ⅰ中第n层膜随机选取个体与单细 胞Ⅱ第n层膜中随机选取的个体 bn,r进行交换。

c.单细胞与中心细胞的交流

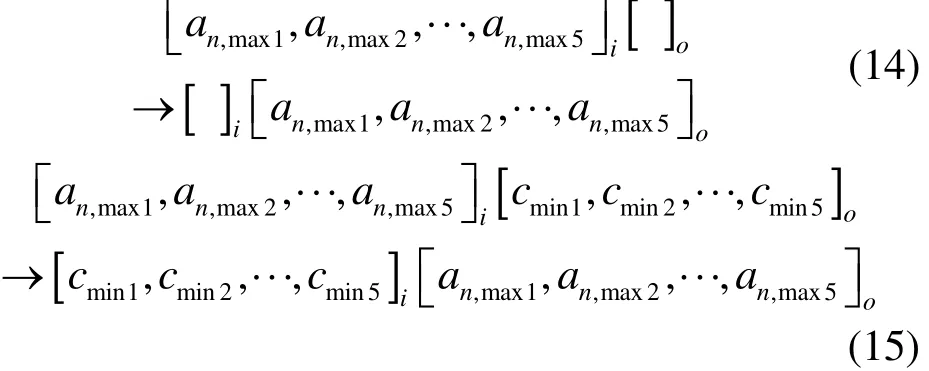
式中：o 为中心细胞；i为单细胞；cmin为中心细胞中最差的个体；式(14)为形成中心细胞初始种群的交流准则；式(15)为第二次迭代时的交流规则；这样的交流准则让每个单细胞中最好的个体都汇聚到中心细胞中。

2.2 新型混合粒子群算法的实现

基本粒子群算法[13-14]是模仿鸟类捕食的原理，目前用于规划DG在配电网中的位置和容量已十分成熟[15-16]。粒子群算法结构简单、易于实现。单个粒子通过跟踪个体极值pp和群体极值gp更新速度；再根据速度确定粒子位置；最后找到最优的粒子。粒子的位置和速度更新公式表示为

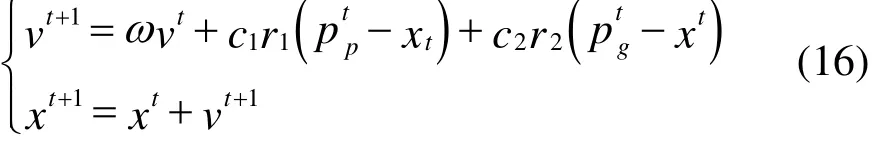
式中：w为惯性权重；c1和 c2为学习因子；r1和 r2为分布于 [0,1]区间的随机数；t为当前迭代次数； pt， 为当前个体极值和全体极值； vt、 xt为当前代粒子速度和位置。粒子群算法收敛速度快，但为平衡局部收敛和全局收敛，对惯性权重和学习因子按式(17)、式(18)进行动态调整。

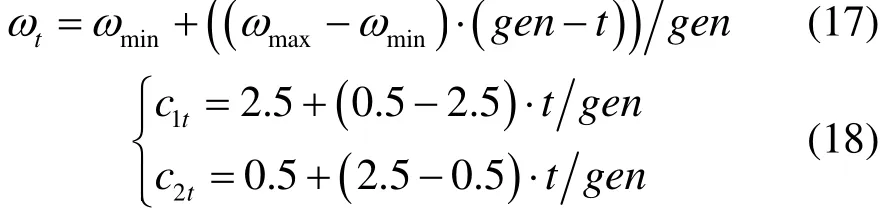
式中：tw为第 t代时的惯性权重；maxw 为最大惯性权重；minw 为初始惯性权重；t为当前迭代次数；gen为迭代次数；1tc 和2tc 为当前代的学习因子。粒子位置和速度更新公式变更为

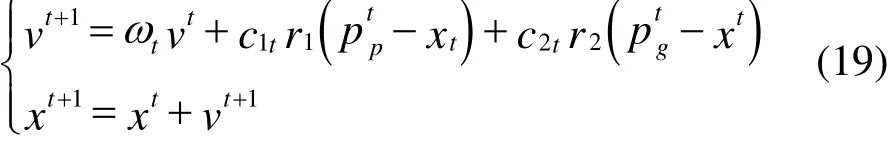
新型混合粒子群算法中的交叉操作和变异及混沌扰动操作过程的实现详见参考文献[9]。

2.3 遗传组织膜和新型混合粒子群算法在扩展规划中的实现步骤

遗传组织膜算法中新建线路为变量，采用实数编码，0表示该线路不新建，1表示新建。为了保证线路初始解的可行性，采用根节点融合法产生初始网架结构[17]，通过遗传选择、交叉、变异、交流规则操作来确定在含DG时最好的配电网线路网架结构。同时考虑到DG的位置和容量的不同对网架结构规划的影响也不同，故外层循环以DG的位置和容量为变量，DG 的初始解根据新增负荷的总容量和节点负荷容量来确定，采用新型混合粒子群算法对DG进行优化更新，再反馈到内层循环更新网架结构。如此循环直到满足终止条件位置。

具体的实现步骤如下：

(1) 输入配电网网络和算法中的相关参数；内层迭代次数初始值 k=0，外层迭代次数为 gen；

(2) 生成 DG 位置和容量的初始解，本文是根据DG 接入的总容量限制和每个负荷节点允许接入的容量来确定的；

(3) 采用根节点融合法[16]产生配网初始线路结构的可行解；

(4) 含 DG 的潮流计算，计算每个单细胞每层膜中个体适应度值并将适应度值排序；

(5) 判定内层遗传组织膜算法是否达到最大迭代次数，若是则跳至步骤(6)，否则依次执行步骤(8)、(9)、(10)、(11)；

(6) 跳至外层 DG 位置与容量的优化程序，并判定算法是否达到最大迭代次数，若是则输出结果，否则跳至步骤(7)；

(7) 调用新型混合粒子群算法对 DG 的位置和容量进行优化，优化后跳转至步骤(4)；

(8) 将每个单细胞的每层膜区域里面的所有个体进行选择、交叉、变异遗传算子操作；

(9) 进行单细胞中膜与膜、单细胞与单细胞间的交流操作；

(10) 判定是否为内层算法第一次迭代，若是则选择每个单细胞中最外层膜中最好的几个个体形成中心细胞的初始种群，否则转至步骤(11)；

(11) 每个单细胞最外层的优秀个体与中心细胞里的个体进行交流，更新中心细胞中的群体，然后跳转至步骤(4)。

基于遗传组织膜算法和新型混合粒子群算法的含DG的配电网双层扩展规划流程图如1所示。

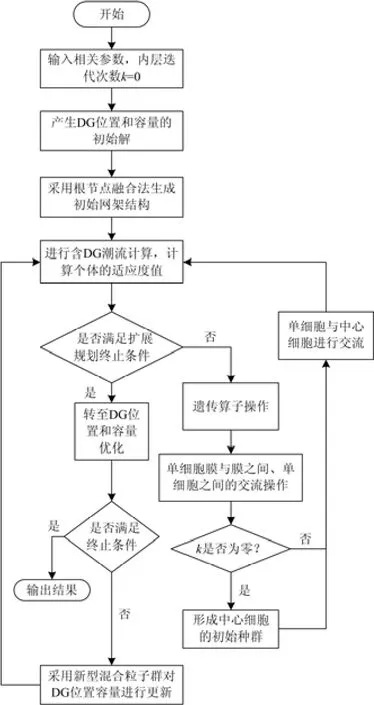
图1 基于遗传组织膜和新型混合粒子群算法的含 DG的配电网双层扩展规划流程图Fig. 1 Flow chart of DG in distribution network double expansion planning based on the genetic organization membrane and the new hybrid particle swarm optimization algorithm

3 算例分析

采用某 10 kV 的中压配电网络为测试系统。配电网初始网架结构如图2所示：实线为已有支路，虚线为可建支路；已有3个节点2条支路，要扩建成 10 个节点的辐射网络，可扩建的支路数为 14 条。其中 2-10 节点为负荷节点，均可接入 DG，每个 DG的功率因素为 0.9，最大 DG 接入总量不超过新增负荷总量的 10%。配电网测试系统的负荷、支路参数来自文献[18]。

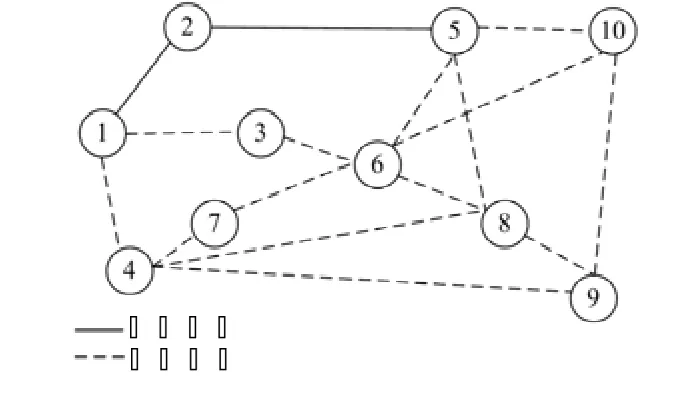
图2 初始配电网络结构Fig. 2 Distribution network before expansion planning

遗传组织膜算法的参数设置如下：单细胞个数为 6，每个单细胞的度为 3；只有一个中心细胞；区域种群数为 30，交叉率 Pc 为 0.8。新型混合粒子群算法的参数设置：粒子种群数为 30，最大迭代次数为 60。

根据遗传组织膜和新型混合粒子群算法在扩展规划中的实现步骤，在 Matlab 上运行 30 次，不含 DG 和含 DG 的扩展规划结果见图3 和图4，分布式电源的安装位置与容量见表1。

未考虑DG时，扩展规划出的网架结构的系统网损为 141.285 9 kW，将 DG 与网架结构综合规划后系统网损为 97.844 7 kW，网损降低了 30.747%。由表2可知DG的引入导致规划的网架结构也有所变化，改变了规划路径，使得规划更加合理，节约了线路新建费用和网损费用。DG 接入后，年综合经济效益为 11.843 6 万元，验证该规划方案的有效性，对降低经济成本有一定的效果。

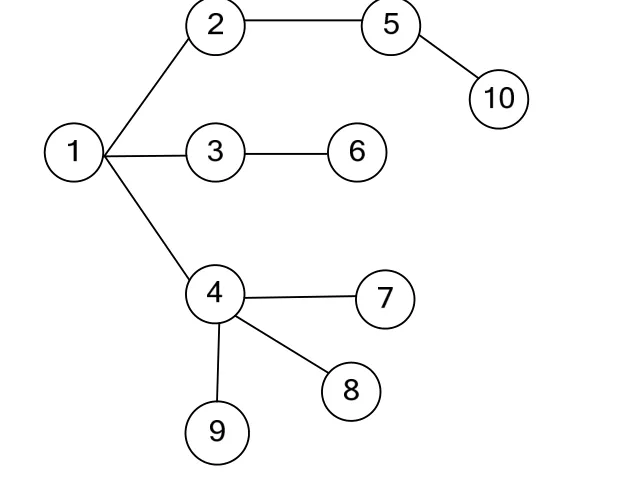
图3 不含 DG 的扩展规划结果Fig. 3 Expansion planning without DG

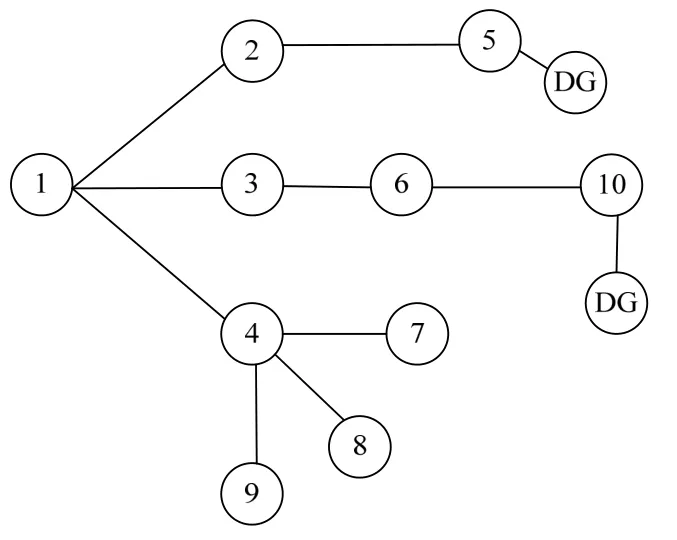
图4 含 DG 的扩展规划结果Fig. 4 Expansion planning with DG

表1 DG 的安装位置与容量Table 1 Installation location and capacity of DG

由表1可知，分布式电源在负荷中、末端，而且 DG 接入后，对配电网的网架结构有一定的影响。

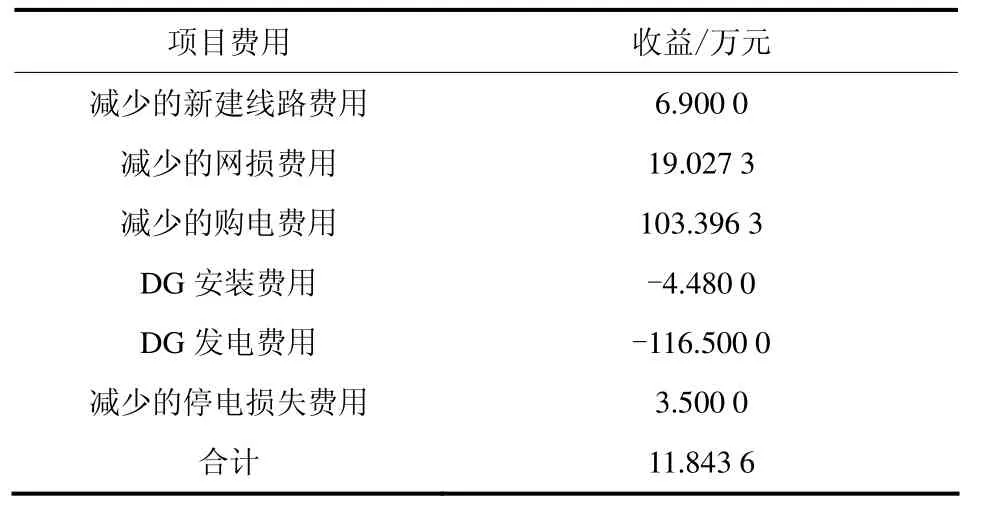
表2 接入 DG 后的年综合经济效益Table 2 Access to DG after years of comprehensive economic benefits

DG的接入还提高了节点电压，电压仿真图形如图5，节点电压最小点由 0.950 4 p.u 上升为 0.966 6 p.u.,增强了电压稳定性，提高了用户用电可靠性。

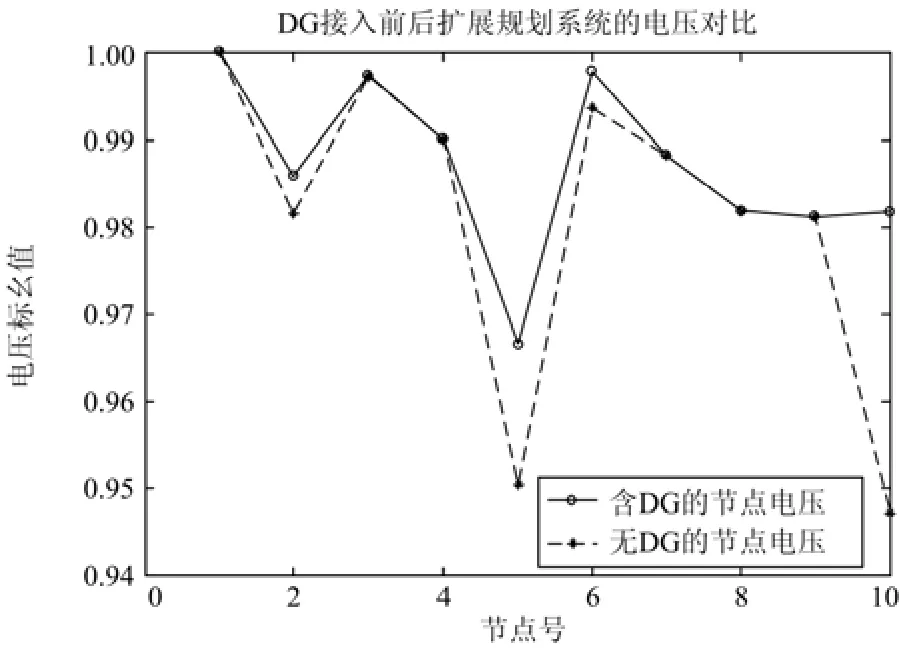
图5 电压仿真对比图Fig. 5 Comparison of voltage simulation

4 结论

(1) 分布式电源在配电网扩展规划中是很重要的。考虑DG的位置和容量对电网的影响后改变了网架结构，使得线路布局更合理，节约了新建费用和网损费用。而且由于DG的加入，提高了节点电压，为用户可靠用电提供了保障。

(2) 本文内层采用遗传组织膜算法规划线路，外层采用新型混合粒子群算法优化DG容量和位置。这种双层优化的准则，使得内外层的优化结果相互影响，规划出的综合优化方案更加合理。并对优化结果以节约成本是否最多为评估方案优劣的标准，结果表明采用这种分层算法综合优化线路、DG 位置和容量取得了一定的经济效益。

[1]肖峻, 崔艳妍, 王建民, 等. 配电网规划的综合评价指标 体 系 与 方 法 [J]. 电 力 系 统 自 动 化 , 2008, 32(15): 36-40. XIAO Jun, CUI Yanyan, WANG Jianmin, et al. A hierarchical performance assessment method on the distribution network planning[J]. Automation of Electric Power Systems, 2008, 32(15): 36-40.

[2]高艺文, 刘俊勇, 雷成, 等. 考虑配电网结构变化的DG 规划[J]. 电力系统保护与控制, 2014, 42(4): 40-46. GAO Yiwen, LIU Junyong, LEI Cheng, et al. DG planning considering the variation of the distribution network structure[J]. Power System Protection and Control, 2014, 42(4): 40-46.

[3]柳睿, 杨镜非, 程浩忠, 等. 分布式电源并网的综合评价[J]. 电力系统及其自动化学报, 2013, 25(1): 34-39. LIU Rui, YANG Jingfei, CHENG Haozhong, et al. Comprehensive evaluation of grid-connected distributed generation[J]. Proceedings of the CSU-EPSA, 2013, 25(1): 34-39.

[4]任洪伟, 韩丛英, 裴玮, 等. 基于多目标优化模型的分布 式 电 源 选 址 方 案 研 究 [J]. 电 力 系 统 保 护 与 控 制 , 2013, 41(24): 64-69. REN Hongwei, HAN Congying, PEI Wei, et al. Research on distributed generation locating based on multi-objective optimization model[J]. Power System Protection and Control, 2013, 41(24): 64-69.

[5]张新松, 张沈习, 袁越. 含分布式风电源的配电网网架规划[J]. 电力系统保护与控制, 2012, 40(13): 1-6. ZHANG Xinsong, ZHANG Shenxi, YUAN Yue. Grid planning for distribution network with distributed wind generators[J]. Power System Protection and Control, 2012, 40(13): 1-6.

[6]HAFFNER S, PEREIRA, L F A, PEREIRA L A, et al. Multistage model for distribution expansion planning with distributed generation-part II: numerical results[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 924-929.

[7]吴万禄, 韦钢, 谢丽蓉, 等. 含分布式电源与充电站的配 电 网 协 调 规 划 [J]. 电 力 系 统 保 护 与 控 制 , 2014, 42(15): 65-73. WU Wanlu, WEI Gang, XIE Lirong, et al. Coordinated planning of distribution network containing charging station and distributed generation[J]. Power System Protection and Control, 2014, 42(15): 65-73.

[8]张 跃, 杨汾艳, 曾杰, 等. 主动配电网的分布式电源优化规划方案研究[J]. 电力系统保护与控制, 2014, 43(15): 67-72. ZHANG Yue, YANG Fenyan, ZENG Jie, et al. Research of distributed generation optimization planning for active distributed network[J]. Power System Protection and Control, 2014, 43(15): 67-72.

[9]何頔, 张彼德, 龙杰, 等. 基于新型混合粒子群算法的含分布式电源的配电网规划[J]. 水电能源科学, 2014, 32(12): 191-194. HE Di, ZHANG Bide, LONG Jie, et al. Distribution network planning with distributed power supply based on new hybrid particle swarm optimization algorithm[J]. Water Resources and Power, 2014, 32(12): 191-194.

[10]黄 亮 . 膜 计 算 优 化 方 法 研 究 [D]. 杭 州 : 浙 江 大 学 , 2007. HUANG Liang. Research on membrane computing optimization method[D]. Hangzhou: Zhejiang University, 2007.

[11]周明, 孙树栋. 遗传算法原理和应用[M]. 北京: 国防工业出版社, 1999.

[12]李俊, 邓大上, 房鑫炎, 等. 考虑电压稳定裕度约束的点 估 计 随 机 最 优 无 功 调 度 方 法 [J]. 电 工 技 术 学 报 , 2015, 30(7): 27-33. LI Jun, DENG Dashang, FANG Xinyan, et al. Stochastic optimal reactive power dispacth method based on point estimation considering voltage stability margins[J]. Transactions of China Electrotechnical Society, 2015, 30(7): 27-33.

[13]傅小利, 顾红兵, 陈国呈, 等. 基于柯西变异粒子群算法的永磁同步电机参数辨识[J]. 电工技术学报, 2014, 29(5): 127-131. FU Xiaoli, GU Hongbing, CHEN Guocheng, et al. Permanent magnet synchronous motors parameters identification based on cauchy mutation particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 127-131.

[14]王振树, 卞绍润, 刘晓宇, 等. 基于混沌与量子粒子群算法相结合的负荷模型参数辨识研究[J]. 电工技术学报, 2014, 29(12): 211-217. WANG Zhenshu, BIAN Shaorun, LIU Xiaoyu, et al. Research on load model parameter identification based on the CQDPSO algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 211-217.

[15]纪震, 廖惠连, 吴青化. 粒子群算法及应用[M]. 北京:科学出版社, 2009.

[16]庄园, 王磊. 分布式电源在配电网络中优化选址与定容 的 研 究 [J]. 电 力 系 统 保 护 与 控 制 , 2012, 40(20): 73-78. ZHUANG Yuan, WANG Lei. Research of distributed generation optimal layout and capacity confirmation in distribution network[J]. Power System Protection and Control, 2012, 40(20): 73-78.

[17]杨文荣, 吴海燕, 李练兵, 等. 配电网中基于人工鱼群算 法 的 分 布 式 发 电 规 划 [J]. 电 力 系 统 保 护 与 控 制 , 2010, 38(21): 156-161. YANG Wenrong, WU Haiyan, LI Lianbing, et al. Planning of distribution network with DG based on artificial fish swarm algorithm[J]. Power System Protection and Control, 2010, 38(21): 156-161.

[18]杨期余. 配电网络[M]. 北京: 中国电力出版社, 1998: 42-57.

(编辑 葛艳娜)

Double distribution network expansion planning including distributed power

ZHANG Bide, HE Di, ZHANG Qiang, DENG Jun, LONG Jie
(School of Electrical and Information, Xihua University, Chengdu 610039, China)

Considering the effect of distributed power on grid structure of the distribution network and without decided capacity and location of the distributed power, the approach of inner and outer layers bi-level programming is adopted for the integrated optimization of the distribution network circuit structure, and the location and capacity of the distributed power. The government subsidy policy is introduced into the objective function, which encourages the use of clean energy, so as to build an objective function module which saves the most economic cost. For the inner layer, with the introduction of the distributed power position and capacity, the tissue membrane computing communication rule is introduced to the genetic algorithm, to enhance the ability of global optimization and computational capabilities, so as to achieve the expansion planning of the network structure; for the outer layer, the new hybrid particle swarm optimization algorithm is adapted to determine the location and capacity of the distributed power. Examples show that the algorithm applied to distribution network expansion planning including distributed power saves the cost, improves the reliability of electricity, and demonstrates the effectiveness of the algorithm.

distributed power; distribution network; expansion planning; genetic tissue membrane; new hybrid particle swarm optimization algorithm

TM715

1674-3415(2016)02-0080-06

2015-04-01；

2015-06-10

张彼德(1975-)，男，博士，教授，研究方向为电力系统规划；

何 頔(1987-)，女，硕士研究生，研究方向为电力系统规划；E-mail: 263713421@qq.com

张 强(1987-)，男，硕士研究生，研究方向为海上风电场过电压研究。

四川省教育厅重点项目(13ZA0023)；流体及动力机械教育部重点实验室(西华大学)项目(SBZDPY-11-14,13)