基于数学知识分类的认知工具设计原则

☆高鹤　马玉慧（渤海大学，辽宁锦州　121000）



基于数学知识分类的认知工具设计原则

☆高鹤马玉慧
（渤海大学，辽宁锦州121000）

摘要：在中小学教育中，数学作为一门不可或缺的课程，成为了教育教学改革中的重要关注点。课改要求数学教育作为促进学生全面发展教育的重要组成部分，还要充分考虑学生发展和在学习过程中表现出的个性差异，因材施教。目前课件等认知工具盛行，但并不能针对学生的问题进行制作，对学生学习促进作用并不大。文中将数学知识分为两类：几何-空间型数学知识和代数运算型数学知识，针对两类知识的学生学习心理和知识特点，进行设计原则的制定，并通过对几个数学认知工具的设计分析和实验研究，发现制定的设计原则对学生的学习成绩有所帮助，以期为中小学数学教师和研究人员的后续工作提供一些帮助。

关键词：数学知识分类；认知工具；案例；设计原则

一、概念界定

本文研究的是狭义的认知工具，即数学认知工具，它是指基于计算机技术，能够提高学习者数学学习的兴趣，支持数学知识的建构，帮助学习者减轻数学认知负荷，提高数学思考能力、认知能力和空间能力的认知模式媒介。例如：概念图、动画、视频和课件等。

二、基于数学知识分类的认知工具设计原则

常见的数学知识可以分为几何-空间型数学知识和代数运算型数学知识。

（一）几何--空间型数学知识的设计原则

几何-空间型数学知识具有空间性，又具有逻辑演绎的特点。学生可以通过利用直观图形、实际的操作和演示来加深印象，增添学习中的实验性。图形的综合性，可以将更多的特征信息或背景因素展现出来。

几何-空间型知识常见的认知障碍是，二维图形只能展示某一点的特殊情况，或学生定势于标准图形，无法摆脱静态图形的限制；由二维静态信息来呈现三维情境，或反过来，维度上的差异会导致视觉“失真”，起初学生理解起来比较困难，无法把孤立的成分整合成有序的意义结构，无法理解图形背后隐藏的几何概念，只能注意到没有联系的事实；几何语言与文字语言互译不正确。

根据对上述特征和认知障碍的分析，笔者针对知识特点和发现的问题，总结出如下设计原则。

1.视觉构造——帮助二维平面与三维空间的转化

空间能力，是许多学科学习中最重要的能力，如数学、物理、化学、科学等，有研究表明：人脑皮层中针对的数学学习的认知支持网络，具有分布式的特点，这意味着数学的多重表征结构得到人脑认知支持。分布式认知网络结构相较于其它具有精确语言表征的结构，本身具有较强的进化发展空间、更多的视觉空间特点[1]。学生在学习三维立体几何数学知识时，常常受到空间、材料和思维定势的束缚，习惯于二维平面的感知，但对三维空间、透视等，缺乏将二维平面转化成三维立体的意识，保持和迁移能力很低。

随着多媒体技术的迅速发展，三维技术已经被引入教育，帮助提高空间能力的学习。很多研究证明，多媒体技术，如果设计合理则可以提高学生的表现。近年来，许多多媒体技术与三维动画或软件系统的应用也已被证明可以有效提高学生的空间能力。

所以，在设计此类认知工具的时候，要将原本需要学生进行大容量认知负荷的思维抽象转化为空间动态，化二维抽象为三维动画，有利于学生加强平面几何与立体几何的学习。

这个案例中的数学认知工具，是一个多媒体学习环境下的学习系统，目的是为了提高学生的空间能力。在这个系统中，可以用动画模拟二维图形折叠成立方体的形状，或立方体扩展成二维图形等。在学习的过程中，提出一个折叠或展开的问题，然后让学生思考并提交答案，此时系统会给出答案“真”或“假”[2]，根据学生对这个问题的答案提供一些线索（即“思考为什么这个二维图不能被折叠成一个立方体，以及如何改变现有这种展开图形的形状的摆放被折叠成立方体”），如果学生按下“折叠”按钮，提示动画将被播放。这些动画可以用三维动画软件制作完成，模拟二维图形如何折叠的立方体的过程，或是不能折叠成的过程。动画与提示的模型（如图1）。

此案例通过在实验室中分组前后测的实验证得，三维动画确实是提高学生的空间能力的有效方法。而且，此案例中的三维动画也有利于提高学生有关二维图形和三维图形之间转换的空间想象能力。在进行如上空间体折叠的认知工具设计中，还可以利用Flash制作成为交互性更强的版本，在现有功能的基础上可以通过加入简单的脚本语言，如鼠标点击左键进行折叠，通过点击右键进行展开，让学生实时看见折叠或展开的动态。

2.图形分割——化思维抽象为动态变化

杜瓦尔将儿童的几何理解水平分为4类：知觉性理解、构图性的理解、论述性理解和操作性理解。其中，操作性理解是当学生观察一个图形时，可以通过操作图形来得到灵感，而在以不同方式（平移、旋转、缩放等）改变图形之后，得到操作性理解，这些操作使得图形具有启发性的功能。杜瓦尔还强调，任何一个图形都是由几个基本的图形单元所组成的，其中的一些子结构（或者一些基本完形）是解决问题的关键，因此，解决几何空间类的题，关键就在于利用视觉技能把那些关键的子结构分割区分出来[3]。所以在对认知工具进行设计时，应将大图形中的小图形逐一分割，然后通过不同方式（平移、旋转、缩放等）将图形改变之后，发现图形各个部分之间的关系，最终得到答案。

例如：图2中，题目是“在RT△ABC中，∠A=50°，点D在斜边AB上，如果△ABC经过旋转后与△EBD重合，那么这一旋转中心是哪个点？旋转角是多少？”。设计图形中包括两个三角形——△ABC和△EBD，将这个图形中的两个三角形拆成出来，然后经过旋转和平移，得到结论。学生可以通过拖动右侧拉杆条上的点调节旋转△ABC，在拉杆条上会显示旋转的角度。

图2　图形分割原则设计示意图

（二）代数--运算型数学知识的设计原则

代数-运算型数学知识的特点是，具有典型的操作性和潜在的运算过程，其形式化也往往具有直观启发性。代数其实是省略了对象和运算的实际情境，去掉实际语言带有的差别，使其一般化，但也可能使学生无法理解符号的含义。在进行这类知识的分析时，应先用简要的形式表述问题（画图表等），试图简化问题（考虑对称性、固定一些变量、特殊情况等），然后选择观点、重点的性质法则。在纯粹的代数题（代数式的表示、赋值与变形、解方程、不等式的解或证明、函数的表示即函数性质的研究、数列及递推关系的讨论等）方面，等价关系是基础。在代数应用题方面，问题表述的文字转化极为重要，自然语言的句法结构与数学表达式的代数结构是有差异的。此外，还要注意处理问题的方法，要将问题与代数系统建立对应关系，并将问题中的操作或关系以代数系统中的运算呈现。

大多数学生将代数运算看作一种程序规则，而非一个数学对象，有些缺乏形式思维理解能力的学生在将文字题转化成代数时存在问题，比如：认为题意中的文字信息都应被使用，这是学生在建构语意网络时的障碍。根据对上述特征和认知障碍的分析，针对知识特点和发现的问题，笔者总结出如下设计原则。

1.图解文字信息——加强形式思维理解

心理学表明，用不同的方法重新叙述，可以启发解题思路，具有启发功能。图解代数题中的文字信息，可以使学习者在学习代数运算类的知识时，更有效地进行数量分析，也可以使题意理解更加清晰，有效消除学生在对文字题语意转化的障碍。

图解法包括线段图解法、图形图解法以及表格图解法。即将问题用适当的方法重新表征出来，消除掉自然语言的句法结构与数学表达式的代数结构式之间的差异，加强形式思维、逻辑思维的理解[4]。如图3是一个来自台湾的计算应用题设计示意图，题目是“台湾高速铁路有台北到高雄（左营）全长约345公里；沿途经过14个县市及77个乡镇市，从台北到高雄的左营站，沿途一共有板桥、桃园、新竹、台中、嘉义、台南等6个停靠站。请你算一下，如果小明在台中站进站，想购票上车，应该会有几种不同的单车车票可以购买？”对于这类题，教师可以按照题意，用线段图解法将文字信息重新表征，并将重点突出，促进思维形成。

图3　台湾计算应用题设计示意图

2.轨迹跟踪、结论验证

在数学学习中，验证是数学思维的主要内容之一，数学验证可以激发学习者的创造能力，数学验证也是一种学生构建数学的过程。《数学课程标准》强调，在教学时要让“学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动”，所以，验证也是数学教学的基本要求。教师应有目的地创设探究性的学习环境，让学生有充分验证的空间[5]，这就需要在认知工具的设计中，尽量给学生呈现多样化、功能齐备、操作简易的软件平台，学习者就可以在平台上进行简单的操作，或开发有用的功能，通过轨迹跟踪或内部参数公式等方法，得出结论，免去学生生搬硬套之难，不再把运算当作程序，而是一个对象。

如图4中，学生可以自行在软件中输入想要的公式，生成函数图形，开发其斜率计算跟踪功能，学习者自己通过拖拽等方式改变函数切线切点位置，软件动态显示斜率变化，并跟踪显示斜率数值变化线段。学生可以验证结果，并为下一阶段学习打下基础。

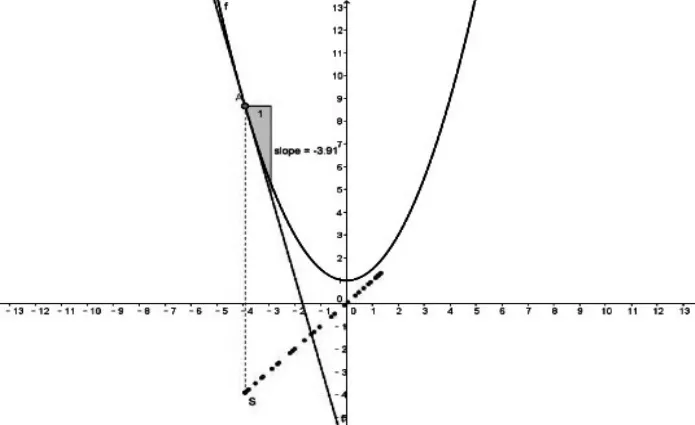
图4　轨迹跟踪、结论验证设计原则示意图

在解题或考试的过程中，很多题目可能需要学生综合运用几类知识进行作答，所以，教师在进行认知工具的设计时，也要全面考虑多种类型的设计原则，将各类设计原则巧妙结合，达到促进学生思维，提高学习效率的效果。

三、实验验证与结果分析

通过上述分析与设计原则，笔者对初高中数学教材进行了试验开发。这里节选出部分内容——主要以北师大版八年级《数学》下册进行展示。这部分涉及的主要内容分为：三角形、四边形的性质；图形的平移和旋转；一元一次不等式方程；分式基本意义及解分式方程等。设计过程中，笔者邀请一线教师——铁岭市支教数学教师张宏家给予指导。经过张老师的分析，学生在学习这部分内容时，有以下需求：（1）图形的平移和旋转是难点，书上语言晦涩，学生学起来有困难，希望相关内容可以更加充分；（2）不知道书上的一些术语，希望给予解释；（3）习题有点少，希望多一些测试；（4）自制力比较好的学生希望多一些拓展学习。

根据前期样本对象和内容的分析，笔者制定了详细的交互支持开发方法，并进行了数学认知工具的开发。本次中学数学认知工具的设计与开发主要基于Windows系统进行，主要采用GeoGebra数学开发工具，GeoGebra需在Java环境下运行，因此，在安装GeoGebra前，先要在计算机中安装Java虚拟机。GeoGebra的功能齐全，其特点是可以跨平台，简单易操作，界面友好，具有较强的交互性，不仅包含了几何、代数、表格和图形，还具备符号计算、微积分、统计等功能。此外，GeoGebra也是非常好的绘图工具。

笔者对两类知识分别进行实验，在教育水平较为不错的辽宁省本溪市实验中学进行。在实施过程中，进行的是随机化实验组、控制组前后测设计，然后对两对实验组和控制组进行两次独立样本T检验，由数据得到：在几何组中F=1.866，显著性概率Sig.=0.176，远大于0.05，证明两组学生前测成绩无显著区别，可以推断几何-空间型知识的实验组和控制组学生水平无显著差异；在代数组中F=1.332，显著性概率Sig.=0.252，远大于0.05，即推测两组学生前测成绩无显著区别，可以断定代数-运算型知识的实验组和控制组学生水平无显著差异。

在对两地进行过T检验后，可以排除前期学习能力的干扰，对实验的后测结果进行单因素方差分析，结果如下：对几何组单因素ANOVA分析结果显示，方差齐性检验值为0.518，检验结果的相伴概率P值相对应于Sig.=0.474，显著水平α设为0.05，满足单因素方差中方差相等的要求；在ANOVA差异分析中，假设在学习中有无认知工具的支持对学生后测成绩影响没有差异，而得到的F=14.930，相应的概率P值Sig.=0.000，应否定原假设，认为有无认知工具的支持对学生学习的后测成绩有显著影响。

在对代数组的单因素ANOVA分析结果显示，方差齐性检验值为3.622，检验结果的相伴概率P值相对应于Sig.=0.061，显著水平α设为0.05，基本满足单因素方差中方差相等的要求；在ANOVA差异分析中，假设在学习中有无认知工具的支持对学生后测成绩影响没有差异，而得到的F=12.045，相应的概率P值Sig.=0.001，应否定原假设，推测有无认知工具的支持对学生学习的后测成绩有显著影响。

参考文献：

[1]董奇,张红川,周新林.数学认知:脑与认知科学的研究成果及其教育启示[J].北京师范大学学报(社会科学版),2005,(03):40-46.

[2] Guo Jiong,Ma Yuhui,Gao He.The impact of using 3D animation in students' spatial ability:Proceedings of the 22nd International Conference on Computers in Education[C], Nara,Noveber 30-December 4,ICCE 2014:379-384.

[3] Duval,R.(1998).Geometry from a cognitive point of view. In: C. Mammana & V. Villani(Eds.),Perspectives on the Teaching of Geometry for the 21st Century, An ICMI Study[Chapter 2.2].The Netherlands: Kluwer Academic Publishers.

[4]高月琴.试论图解法对小学数学解题的作用及实施对策[J].数理化学习,2014,(10):93-100.

[5]朱庆飞.小学生数学验证能力的培养[J].教学月刊小学版,2001, (11):30-32.

[编辑：郑方林；实习编辑：庞洁]

中图分类号：G434

文献标识码：A

文章编号：1671-7503（2016）07-0033-03