数学建模思想在小学教学中的内涵价值

庄惠芬

从儿童数学学习来看，数学建模不是抽象的比赛，而是在日常的数学学习中建立的数学概念、建构的数学方法、获得的数学思想、形成的数学解决问题的能力。因此，有概念模型、方法模型、思想模型等等，是儿童经历数学学习“再创造”的过程，是儿童运用习得的数学模型去观察分析现实问题、解决现实问题的过程，在这过程中获得数学的理解、思维的发展、经验的积累、能力的提升等等。

一、数学建模，让儿童经历数学化过程

课程标准强调的“从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程”，这就是“数学化”的过程。

案例描述：“间隔排列”（摘自星河小学三5班苏畅的数学日记）

“舅舅家的农家乐店要开张了，想在门前挂5个灯笼，然后同时想让灯笼和气球一个隔一个排列，让大家想一想气球可能会有几个？”

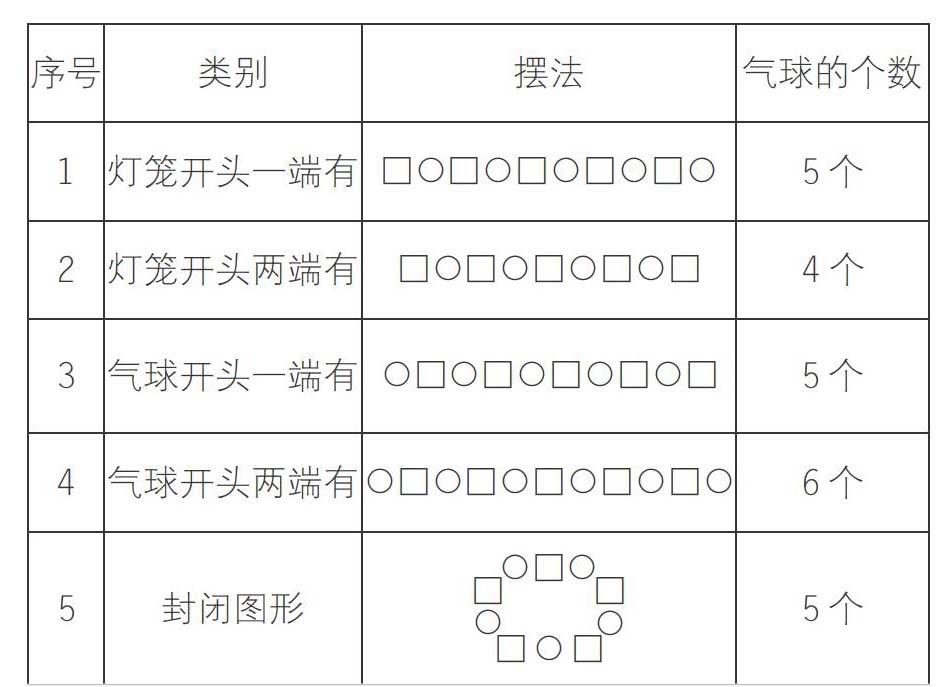
我认为挂气球问题其实就是间隔排列的问题，采用先分类，再画图和列表的方式来解决。我觉得气球和灯笼间隔排列会有两类情况，一类是灯笼开头；另一类是气球开头；而灯笼开头中又有一端是灯笼和两端都是灯笼的情况；气球开头也是一样，有一端是气球和两端都是气球的情况。我用○和□表示气球和灯笼，它们的排列方式如下表：

这样一共就有5种可能，那么如果单独只看气球个数就是有4、5、6这三种可能。所以运用这样的思考，如果我们要在广场上摆放不同花朵，还是道路两旁栽种不同的树木，只要是间隔排列，都可以这样的方式来解决。

1.数学化观察，发现问题

儿童对这一生活问题的观察与发现，则在教材中的一一间隔排列中得到启发，教材中出现了三组场景：手帕和夹子、蘑菇和兔子、篱笆和木桩。从题组场景中可以进行系统化的观察，虽然有不同的生活情境，但是从三组物体的观察中，可发现共同的特点：一一间隔排列。并且也逐步建立了两端物体、一端物体，以及两端都没有物体等基本的数学模型；这样的数学建模经验为解决张挂灯笼和气球问题奠定了基础，寻找到了联系，同样通过系统化的观察、“数学化”的途径，提取到了要解决问题的信息，将生活问题简化为数学问题。

2.模型的建立，分析问题

儿童从呈现的原型中经历数学化的过程，摒弃非数学因素，概括出了各种可能的共同属性，那就是气球和灯笼之间建立起了一一对应的关系，并且依次不断地重复出现，提出它们共同关键属性的种种假设，建立起灯笼开始与气球开始的不同模型，确立这两类中一端有与两端都有的不同模型，还可能有封闭图形等模型梳理与建立。学生摒除具体情境的影响，进而从事物的内在结构来入手认识规律。

3.模型的解释，解决问题

数学建模是儿童经历对信息的捕捉、发现、选择、简化、整理的过程，是让儿童经历观察、分析、比较、归纳、抽象、概括与反思建构的过程，是数学问题发现、提出、分析、解决的过程，是数学思想、方法、经验、能力积累的过程。在灯笼与气球的排列问题的解决过程中，在构建模型的过程中，可以借助一一对应的思想进行分类，采用画图、列表等方式来进行模型的建立、解释和应用，在不同的数学模型建立的过程中清晰地凸显事物之间的数量关系。

4.模型的拓展，衍生问题

数学知识存在自身的发现、发生、发展、变化的内在规律，数学知识不同因素之间、数学知识内部的小系统之间、数学知识的不同层次之间有着内在的必然的联系和关联，儿童在数学学习中经常有着对数学知识梳理的意识和能力，对数学学习内容进行类化归纳，实行数学模型的“整体集装”。以上问题的解决从一字模型到O字模型，从不封闭图形到封闭图形，学生在辨析中建构自己的图式。如果进一步拓展模型，还可以呈现诸如□○○ □○○ □○○…□○○的开放图式；或者如左图的封闭图式。这样的模型拓展，为学生提供了更具挑战性问题场景。

二、数学建模，让儿童拥有结构化眼光

小学数学建模教学，就是要让儿童在数学化的过程中去发现、抽象、理解数学结构，经历数学知识的发生发展过程，经历从数学原型抽象成数学模型的过程，突出建立数学模型的过程。在这样的过程中数学思维的关联、数学思想的渗透、数学方法的迁移、数学能力的集聚，不断形成教学框架的连续。我们可以想象，每一堂数学之旅所呈现的学习结构、方法层次都将给儿童长久而又持续的熏陶和浸染，儿童的系统思维能力与核心的数学素养也必将提高。

1.把握知识结构。儿童每天所进行的数学课堂的结构在儿童整个数学知识系统的学习中，是一个片段，是一个微型的结构；要用体系化的视界整体上把握知识结构，对已经学过的知识进行分类、梳理、归纳、整合，理清来龙去脉，沟通纵横联系。让儿童所学知识能“竖成线”“横成片”“链成球”“立成体”。数学模型建立的过程是儿童主动学习的过程，也是儿童自我完善和知识结构的过程。

2.形成模型结构。数学就是规律，一般具有一定的结构性特点，是能够进行数学抽象和模型提炼的。数学模型与模型之间可以寻找相应的沟通与联系，将有关联的或者相似的数学模型链接构建成一个个数学模块，从而形成一个网络式的模块体系，在儿童的头脑中形成模型框架。在数学一个阶段、一个单元、一个模块的学习中不断沟通其内在联系，形成自己的模型结构。

3.贯通认知结构。现代研究表明，数学思维的结构与数学科学的结构是十分相似的。头脑中新的数学认知结构的建立，要依赖于数学思维结构的发展。如一组题链，即同一情景下不同形式组成一个知识块。通过对原题的改变，还原生活本原，列举各种的可能变化形式，呈现出不同类型而又相互链接的题组结构和数学模型。教师要研读教材，把握知识的体系。根据教材知识的发展和儿童的认知规律，精心选择和组织“结构化”知识，引导儿童实现自我建构。

因此，我们以数学建模为引擎，从数学结构化的特点与儿童认知结构的特质出发，把握数学模型建立的规律、过程与方式，引领儿童感受并把握数学知识结构、数学的模型结构与儿童的认知结构。

三、数学建模，让儿童建构系统化思维

从头脑里提取记忆信息，寻找学过的数学模型，不断与已知信息之间组织成整体结构，这就是系统思维。系统思维是对事情有一个整体而全面的思考，对事情或问题的产生、展开、发展及问题的解决、结论的获得以及在这个过程中方法的运用、用优化和对未来的影响等一系列问题作为一个整体系统来研究和综合地考察认识对象的一种思维方法。

1.从事理到数理，基于经验的认知建构

从儿童已有的知识和经验来看，生活原型是有丰富的活动经验作支撑的数学事实或现实材料，便于唤醒儿童在头脑中产生数学问题，从生活原型提升为数学模型。在儿童数学学习过程中，积极创设儿童善于建构知识的情景，摄取解决数学问题需要的信息与经验，激发儿童从事理到数理的转化，完善认知建构。

2.从法理到学理，基于能力的方法建构

法理即以整个数学问题的共同发展规律和共同性问题这一数学模型为研究对象。在五年级数学学习中，我增加了“认识菱形”的内容的学习，是以此作为研究的对象，贯通起儿童对于图形的认识的系统思维，获得“菱形的认识”是在知识价值、经验价值，以及思维价值、应用价值、审美价值的过程中获得认识图形的普适性学习方法，即学理。

在图形的模型建构过程中，学生自我建构认识图形的方法：研究什么？研究图形的边、角与特性；怎么研究？可以从不同的角度观察图形，可以从图形的大与小、分与合、剪与拼、割与补进行研究，可以从规则到不规则进行转化，可以从观察猜想——操作验证——比较归纳——得出结论的过程等方面进行方法模型的建构。将菱形置于四边形的大背景中进行认识，辨析其与四边形、长方形、正方形、平行四边形、梯形的逻辑思维关系，经历辨析各四边形之间关系的过程，增强四边形认识的系统性，提高学生的逻辑思维能力与推理能力，使学生形成对四边形的整体认识，形成关于四边形的良好认知结构是有积极意义的。

小学数学建模的主体是学生，数学建模教学就在日常的数学教学中。在这个过程中，要培养学生主动建模的意识，经历数学建模的过程，不断发展建构数学模型的能力。