基于聚类思想的交通信号相位组合优化研究

陈文斌，林　菁，胡昌君

(西南交通大学交通运输与物流学院，四川 成都 610031)



基于聚类思想的交通信号相位组合优化研究

陈文斌，林菁，胡昌君

(西南交通大学交通运输与物流学院，四川 成都 610031)

摘要：为合理地进行信号相位组合的优化设计，从单点信号控制交叉口车辆运行特性出发，对相位组合优化问题进行分析。首先定义相位绿灯时间的相对利用率，在此基础之上，将相位内交通流的组合优化问题抽象为不同交通流对象之间的聚类问题，运用聚类分析方法建立相位组合优化模型。模型选取相位绿灯时间的相对利用率作为聚类结果的检验标准，将交叉口延误时间作为相位组合优化方案的评价指标。通过vissim仿真对比，信号交叉口总延误降低15%左右。

关键词：城市交通；相位组合优化；聚类分析；vissim 仿真；信号交叉口

HCM中提出“信号设计中最为关键的一步就是设计一个合理的相位结构”，相位结构设计是信号配时优化中的首个关键步骤[1]。相位结构是相位相序的统称，它包含了相位组合方案和相位切换方案，相位组合方案用以描述允许同步获得通行权的多股交通流组合关系[2]。国内外关于交通信号控制的研究，大多集中在对信号配时优化研究，认为只要建立一个科学的信号配时模型就可以实现信号交叉口的最优化控制，而有关信号配时的研究往往建立在既定的相位组合方案之上，忽略了相位组合方案本身的优化[3]。

在国外，相位结构的设计主要形成了2种理念[4-5]：基于相位控制的设计理念和基于车流控制的设计理念。前者是相位确定的基础上进行配时的优化，主要代表有Webster、Imptota、Allsop[3]；后者从适应车流的角度出发考虑允许一股车辆在多个相位内通行，R.Akcelik详细的论述了车流控制理念[6]。相位结构设计最重要的一条原则是车流均衡原则，包含了相位内部车辆均衡和相位间的车流均衡两层意思。然而这两种理念都存在着一定的弊端，都不能兼顾车流均衡原则的两层含义。国内有关相位结构的研究大多集中在相位方案的切换问题上：王若峥等[7]利用Petri网对交叉口建模分析,论证了相位的转换次序能提高交叉口的通行效率；向伟铭等[8]将过饱和交叉口的车辆排队问题抽象为离散时间切换系统的指数稳定性问题，通过设计状态反馈机制调整绿灯时间实现信号控制的有效切换；柳祖鹏等[9]通过设计绿灯相位、红灯相位下的绿灯需求度，利用相位切换系统实现公交信号优先控制。而对于相位组合的优化研究甚少，徐良杰等[10]首次采用聚类的思想进行相位组合优化，为相位组合优化提供一种新的方法，然而作者仅考虑了交通量对相位组合方案的影响，缺少对交叉口几何特征影响因素的考虑。

本文在前人研究的基础之上，根据交叉口车辆运行特性，从相位结构设计意义出发阐述相位组合问题，并依据聚类原理建立分时段相位组合的优化模型。该模型能很好地应用于交通流存在较大差异的路口，通过科学的方法确定最优化关键车道组的组合，提高交叉口通行效率。

1相位组合与聚类分析的优化分析

1.1相位组合优化原则

信号交叉口交通设计的两大主要目标是安全和效率，为了更好地实现设计目标，机动车相位优化设计应遵循以下原则：1)车流均衡原则[11]，对于相位组合优化而言，车流均衡原则主要是指相位内部车流的均衡，意在通过相位设计实现相位组合内部各车流的相对均衡；2)相位放行的安全性原则，相位组合设计应尽量避免相互冲突的交通流同时出现在一个信号相位，从而降低交通事故发生率。

1.2相位组合优化原理

交叉口各进口道车流到达交叉口之后，由于受到信号灯组的约束而不能顺利通过，一般情况下可以将其状态描述为：排队—等待—通过(低饱和流率—饱和流率—低饱和流率)—排队的循环过程[12](见图1)。

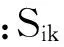
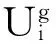
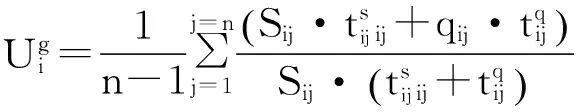
(1)

由此可知，一个合理的信号相位组合方案既要能够满足相位绿灯时间利用率的最大化，又要兼顾相位内车流排队情况，尽量避免二次排队。国内外关于相位的损失时间主要指启动损失和清尾损失时间，而忽略了相位绿灯时间内的相对损失。

1.3聚类思想概述

聚类就是将物理或抽象对象的集合分组成为由相同或近似的对象组成的多个簇的过程。其基本原理是根据数据对象自身的属性，用数学方法按照某种相似性或差异性的指标，定量地确定不同对象之间的亲疏关系，并按这种亲疏关系程度对样本进行聚类。

给定一个对象集合X= {x1，x2，…，xn}，如果将X分成m个集合类C1，C2，…，Cm，且满足以下条件[13]：

Ci≠∅，i=1，2,…,m，

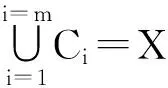
Ci∩Cj=∅，i=1，2,…,m， i≠j，

则将其称为集合X上的聚类。

聚类分析根据聚类规则的不同将数据划分为不同的聚类结果，一般而言，聚类分析包括如表1所示4个步骤。

在研究样本特征属性获得数据矩阵后，为实现样本的合理分类，常常需要定义对象间相似度的计量方法，用以描述对象特征间的相似程度。常用的相似度计量方法有两种，即距离度量和相似性度量[14-15]。

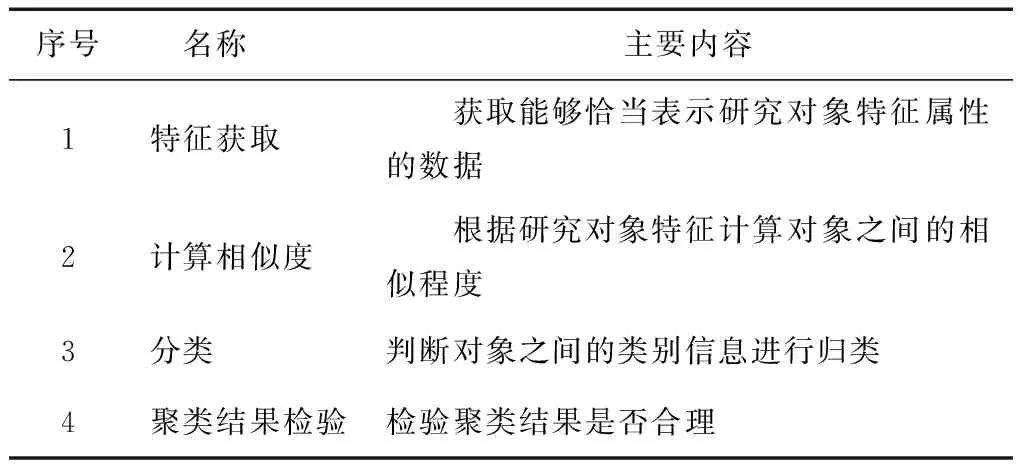
表1　聚类分析步骤

为合理描述各交通流对象间差异的大小，本文采用距离度量的方法，距离越远表示对象间的差异越大。对象间距离定义的方法有很多种，采用的度量公式也就各不相同。常用的距离度量的公式主要有闵可夫斯基距离、欧式距离、绝对值距离、切比雪夫距离等。为真实客观地反应对象间的绝对差异，本文采用欧氏距离来定义各股交通流之间的距离。

2相位组合优化模型

2.1模型的建立

相位交通流组合即在同一时段放行多股相互兼容的交通流，缩短信号周期时长，减小绿灯间隔损失时间，充分利用交叉口的时空资源。信号相位组合的优劣，主要体现在多股交通流在获得相同通行权时车流放行的均衡性；因此，需要对交通流集合U进行分类，使得同类之间的距离最小，类与类之间的距离最大。

假设某一信号交叉口在某段时间内具有n股交通流，且最优相位数目为m，对其进行聚类组合。首先视n股交通流为一类，然后通过规定类与类之间的距离(相似度)，将最为相似的一对合并成为一个新类直到将交通流集合U分成m类为止。数学模型表示为

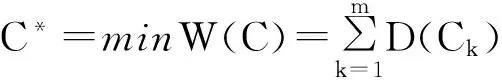
(2)

式中：C*为交通流集合U的最优分类；D(Ck)表示第k类交通流间的距离。类与类之间的距离有很多种定义的方法，本文拟采用欧氏距离平方定义类与类之间的距离。欧式距离平方相对比较简单直观，能真实反应对象之间的距离，但也存在着明显的缺点，它将研究对象的不同属性之间的差别等同看待，这一点往往跟实际情况是不相符的；因此，为更合理地反应研究对象间的差异程度，需要根据对象特征属性的不同对公式进行合理的调整。

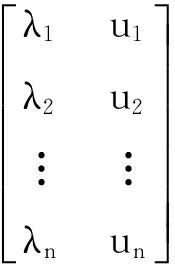
将车辆通过信号交叉口的过程看成是车辆依次排队等待服务的一个过程，选取车道组车流平均到达率λi(到达强度)及该车流在相位绿灯时间内的交叉口的平均服务率ui(服务强度)作为各股交通流的特征值，即xi=(xi1，xi2)=(λi，ui)，其中l=2，对象的数据矩阵为

(3)

由于第i车道组车流平均到达率λi和交叉口对其平均服务ui是描述车流到达和离去的2个相反特征属性，因此不能直接利用欧式距离平方直接度量类与类之间的距离，需要通过修正。将数据矩阵修正后的结果如下：

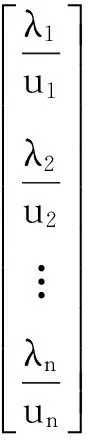
(4)

因此，类与类之间修正后的欧式平方距离为

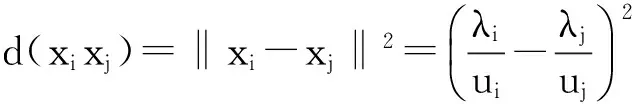
(5)

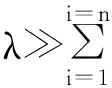
其中

(6)

式中δij为第i股交通流和第j股交通流之间的冲突系数。可以得到如下n股交通流冲突距离矩阵：

(7)

距离矩阵如下：

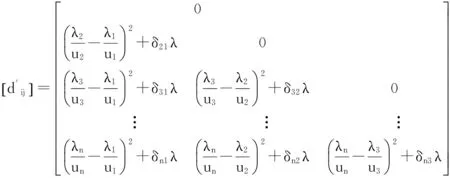
(8)

根据相位设计基本原则，相位组合优化即实现相位内车流均衡。它是针对某一特定相位确定阶段的效率评价，旨在使各个相位组合中每股车流到达和离开交叉口的动态过程能够达到相对均衡，因此，相位组合优化目标模型如下：

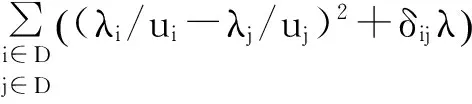
(9)

2.2模型标定及求解

从周期时间的角度考虑，应尽量采用最少的相位分开冲突车流，这是一项很有意义的工作。韩强等[16]结合图论的相关知识，对常见信号交叉口最优相位数目进行求解，文中以此作为相位数目m的参考取值。λi和ui作为交叉口各股交通流的特征值，应通过实地调查获得。

在获取相关参数之后，鉴于模型参数较少且简单，利用Matlab进行简单编程计算即可获得相位组合优化结果，具体参考算例。

3案例分析

选取某市一单点信号控制十字型交叉口作为分析对象，东西、南北均为双向8车道，各有一条专用左转车道和专用右转车道。该交叉口信号配时方案：东西直行绿灯时长21 s，东西左转14 s，南北直行18 s，南北左转11 s，每个相位后各有黄灯时间3 s和黄灯时间1 s，周期总时长为82 s。通过实地调查，各进口道不同转向的交通量如表2所示，各进口道的特征参数如表3所示。

表2　各进口道交通流量

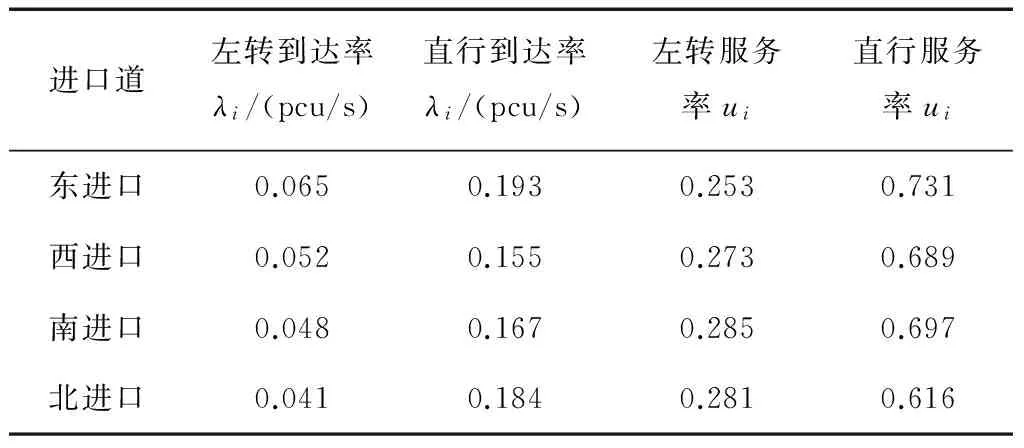
表3　各进口道的特征参数

根据以上参数，利用相位组合优化模型，并通过Matlab计算得到最优相位组合聚类结果为：第1相位为东进口直左，第2相位为西进口直左，第3、4相位分别为南北直行、南北左转。在采用同周期的前提下，利用Webster公式计算得到各自的绿灯时长分别为18、15、20、11 s，黄灯时间和全红时间分别为3、1 s。

表4相位组合优化前后相位绿灯时间的相对利用率

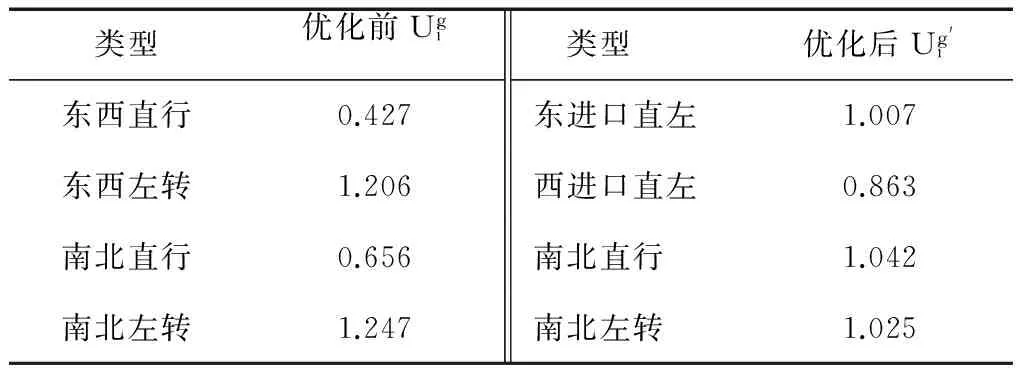
类型优化前Ugi东西直行0.427东西左转1.206南北直行0.656南北左转1.247 类型优化后Ug'i东进口直左1.007西进口直左0.863南北直行1.042南北左转1.025

表5　相位组合优化前后延误时间

经过仿真得出优化前后交叉口总延误降低15%左右，其中东进口左转延误降低程度最为明显。这主要是由于传统相位组合观念的束缚，东西直行往往放在同一个相位，忽略了东进口左转交通流的实际情况，导致左转延误严重。同时，优化后南北直行相位的绿灯时间延长，适应交通流需求情况延误减少。

4结论

相位结构设计作为信号控制中最为关键的一步，它不仅跟交通流的动态变化有关，而且跟交叉口的几何特征等多个因素存在着联系，这导致传统的相位组合方式难以确定最优相位组合方案。本文在分析相位组合优化问题的基础之上，利用聚类思想建立相位组合优化模型，并验证了聚类结果的合理。仿真结果表明：相位绿灯时间的相对利用率明显提高，且二次排队现象也得到一定程度上的缓解；交叉口总体延误降低15%左右，交叉口通行效率得到明显提高。从优化结果可以看出，相位组合优化对于实现交叉口的最优控制具有非常重要的意义。聚类思想的运用为相位组合优化提供了重要的理论支撑，优化结果令人满意，对于改善城市交通拥挤具有重要的应用价值。

参考文献

[1]TRB. Highway Capacity Manual (HCM) 2000[R]. WaShington DC：National Research Council, 2000.

[2]徐洪峰，李克平，郑明明. 基于逻辑规则的单点公交优先控制策略[J]. 中国公路学报，2008，21(5):96.

[3]王京元.信号交叉口时空资源综合优化实用方法研究[D]. 南京：东南大学，2006:3.

[4]唐绍杰.单点、定时、多相位信号配时和渠化[D].上海:同济大学，1993.

[5]王浩.交通信号相位相序问题研究[D].上海:同济大学，2002:18-47.

[6]Akcelik R.Traffic Control Signals :Capacity and Timing Analysis[J].ARRB,1981,10:56.

[7]王若峥，曹立明，王小平. 基于Petri网技术的交通信号相位调节研究[J].计算机应用于软件，2006，23(4):71.

[8]向伟铭，肖建，蒋阳升.基于切换系统的过饱和信号交叉口混杂控制[J].交通运输系统工程与信息，2014，14(2):57.

[9]柳祖鹏，李克平，倪颖. 基于绿灯需求度的单点公交信号优先控制策略[J].同济大学学报(自然科学版)，2013，41(3):408.

[10]徐良杰，王炜.基于有序样本动态聚类的信号相位相序优化模型[J].公路交通科技，2006，23(4):120.

[11]Research Management Center. Florida Intersection Design Guide of New Construction and Major Reconstruction of at-Grade Intersection on the State Highway System[R].FDOT,Florida:[s.n],2002.

[12]全永燊.城市交通控制[M].北京：人民交通出版社,1989:11-15.

[13]宋媛.聚类分析中确定最佳聚类数的若干问题研究[D]. 延吉：延边大学，2013:3-12.

[14]唐东明.聚类分析及其应用研究[D].成都：电子科技大学，2010:20-40.

[15]曹永春，邵亚斌，田双亮，等.一种基于分组遗传算法的聚类新方法[J].西华大学学报(自然科学版),2013,32(1):39.

[16]韩强，刘治平. 圆染色在城市交叉路口交通信号相位个数设计中的应用[J].工程数学学报，2005，23(5):775.

(编校：夏书林)

Signal Phase Composition Optimization Based on Cluster Algorithm

CHEN Wenbin，LIN Jing，HU Changjun

(SchoolofTransportationandLogistics，SouthwestJiaotongUniversity，Chengdu610031china)

Abstract:In order to design the signal phase composition rationally, starting with the figure of vehicle operating characteristics, we defines the relative utilization of phase green time by analyzing the phase combinations. Thus, the problem of traffic composition is viewed as clustering problem, and a phase combinatorial optimization model is constructed .By selecting relative utilization of phase green time and delay time as evaluation index of phase combinatorial optimization, through the comparative analysis of vissim simulation, total delay of signalized intersection is reduced by about 15%. This provides a new method for signal phase structure design.

Keywords:urban traffic；phase combinatorial optimization；cluster algorithm；vissim simulation；signalized intersection

收稿日期：2015-01-10

中图分类号：U491.4

文献标志码：A

文章编号：1673-159X(2016)03-0040-5

doi:10.3969/j.issn.1673-159X.2016.03.009

第一作者：陈文斌(1988-)，男，硕士研究生，主要研究方向为交通控制。

·新能源汽车与低碳运输·