既然殊途，自不同归

◇张齐华

既然殊途，自不同归

◇张齐华

都说，殊途可以同归。然而，在数学教学的道路上，不同的路径选择往往面临着不同的归宿，有时竟然相去甚远。

翻阅各版本数学教材中的“用方向和距离确定位置”一课，编排虽各有侧重，但总体思路均脱不开“告诉”二字。想来也自有其理，毕竟，诸如“北偏东”“南偏西”等描述方向的方式，原本便是现实生活与数学领域的一种人为规定。既是“规定”，“告诉”便也不失为合适的选择了。

可是，教材作如是选择，并不代表我们的教学也应亦步亦趋。除了教材这一基本的教学线索，我们的课堂还可以有怎样的新空间、新想象和新可能？为此，一个月的时间，便有了一次基于不同教学立场与意趣的课堂探索。

一 基于“理解”的数学学习

“北偏东”也好，“南偏西”也罢，现实生活中，学生的确鲜有接触。毕竟，日常生活中，东北、西南等描述大致方位的名词，加上约略的距离估测，已足以应付日常生活之所需。

然而，现实经验的缺席是否意味着学生完全不能理解这样的数学表述？已有的方位、角度及距离等数学经验，可否帮助学生“组合”出他们对新知的准确理解？倘若我们不去直白地告诉学生何谓“北偏东”，而是直接以此示之，通过给定“轮船在灯塔的北偏东30°方向3km处”，引导学生结合之前的全部数学经验，自己想办法在平面图中找到这艘船的位置，在我们看来，“寻找”的过程，就是学生理解“方向和距离”的过程，就是学生结合已有的东北方向30°、3km等概念，自主整合出新概念意义的过程。实践证明，学生完全有能力完成对上述概念的理解。问题仅在于，不同的学生对于“北偏东30°方向”究竟应该算“从北开始向东偏30°”还是“从东开始向北偏30°”，这一问题在理解上存有一定分歧。当然，这一分歧本就在我们的预料之中，也是我们乐于遇见的。因为，倘若没有这样的分歧，上述的教学任务设定，无疑就缺乏合理的教学价值，也缺失学习过程中必要的对话、争论直至达成共识的丰富过程。

于是，面对生活中并不常见的数学表述，问题呈现、尝试作图、对话碰撞、实现理解，便成为我第一轮尝试的基本路径，总体效果不错。

二 基于“探索”的数学学习

进行第二次尝试，缘于笔者所在区域的一次教研活动。受邀参与磨课，课题正是“用方向和距离确定位置”。由于自己刚上过这一课，对此颇有心得。但考虑到，如果只拿着上述教学路径再唱“同一首歌”，未免心有不甘。毕竟，这次是别人上课，“站着说话不腰疼”，何不把步子迈得更大一些，来一次更开放的探索！磨课过程中，你一言、我一语，新的教学线索也渐渐明晰起来。大家一致认为，既然学生可以理解“北偏东30°”这样的数学概念，那么，我们是否也应有足够的信心，相信学生是可以基于原有的数学经验自己来建构“北偏东30°”这样的数学表述的呢？倘若不能，能够建构起类似的表述也未尝不可。至少，我们的教学又向前迈出了一步。

于是，我们给学生呈现了如下问题情境：“茫茫大海上，有一艘船因为出现故障不能行驶，如果我们以灯塔为观测点，那么，我们该如何用数学的方式来确定船所在的具体位置？”为了给学生“解决问题”提供必要的思维支架，我们以灯塔为坐标原点，通过引导学生回忆，给出了平面图中的四个关键方向，并最终呈现了如下的问题情境图：

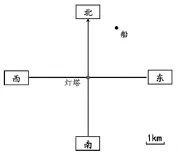
令人欣喜的是，面对开放的问题空间，学生并没有显得茫然无措。相反，在原有知识经验与新的问题情境的不断对话中，在同伴之间的相互启发与碰撞下，四人组建的学习小组很快便有了各自的思维路径和问题解答：“船在灯塔的东北。”“船在距离灯塔3km的地方。”“船在灯塔的东北30°方向3km处。”“船在灯塔的东北60°方向3km处。”“船在灯塔的北向东偏离30°方向3km处。”观察学生学习小组各自给出的解决方案，我们不难发现，尽管他们的思维精细程度呈现出差异，但上述阶梯性递进的学习素材已经足以为教师后续的教学活动奠定良好的基础。即便简约如前两个答案，但他们解决问题的方向至少是准确的。只不过，他们并没有意识到，在二维的平面空间中，只给出了其中一个维度（方向或距离）是没办法准确确定船所在的“点”的。充其量，它只能确定某一个面或某一条线。至于最后一个答案，我们不难发现，虽然他们的表述中没有出现 “北偏东30°”，但数学的理解已经极其接近于此，剩下的，也只是表述的“约定俗成”而已。

最后的教学无疑是成功的。更让人惬意的是，从原先的“基于理解”，到现在的“基于问题之下的探索”，我们将课堂之窗又轻轻推开一扇，窗外更美的风景再次扑面而来。都说“给学生一点空间，他们会还你十分精彩”，此话果真不假。不过，激动之余，也有遗憾存在。总觉得，学生尽管在不同的层面上实现了对问题解决方案的建构，但综观其思维路径，总还是相对单一的。能否在问题的开放性上再作新突破，以实现学生完全开放的学习、建构与创造？或许，我们还可以来第三次。

三 基于“创造”的数学学习

说做就做。这一次的教学，显然是基于某种特定的“教学预期”的。简单来说，我们希望通过“数学问题”的重新设定，能够引发出学生更多元、更开放、更富有创造性的数学思维方法与问题解决策略。事实上，在这一教学预期的背后，隐含着我们对于数学教学更美好、更富理想化的一种假设，那就是：相对于具体的知识而言，探索性活动经验的积累，以及学生在解决问题过程中表现出来的思维的开放性、创造性，无疑是数学教学更重要的目标。为此，我们需要重构教学框架与路径，给学生腾出施展思维拳脚的更大舞台和空间。

那么，上述“基于探索的数学学习”，学生的思维何以只停留在同一方向上？是哪儿出现了问题？课堂观察、个别访谈、思维前测、头脑风暴，我们的目光很快便聚焦于上图包含有东、南、西、北四个方向的“平面直角坐标系”上，观点也渐趋一致：由于对学生问题解决能力的“不够信任”，我们给学生的“问题解决”设定了这样一个思维“脚手架”，而循着这一“脚手架”，学生的思维呈现出某种“趋同性”便不难理解了。

于是，再次教学，我们决定从打破这一“脚手架”开始。不再给学生呈现辅助的教学支持，只呈现“灯塔”“船只”所在的点，辅之以方向的简单提示与比例尺（如下图），剩下的一切，交由学习小组自己想办法来解决。

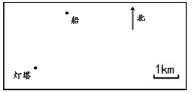
实践再一次证明，第三次的放手，并不是一种盲目的乐观。正如前文所述，由于不再有平面直角坐标系的“辅助”，学生的思维呈现出更大的自由度与开放性。在这一过程中，“船在灯塔的1点钟方向3km处”“船在数对（1.5，2.5） 处”“船在数对（3，5）处”“船在灯塔向东1.5km、向北2.5km处”“船在灯塔东北方向30°3km处”“船在灯塔正北向东偏30°方向3km处”……足够开放的问题空间、自由思考的学习小组、多元互动的师生对话，让原本封闭的、“告诉式”的数学学习，呈现出了令人难以忘怀的思维之光、自由之光、创造之光。在这一过程中，知识本身已不再唯一重要，过程中所折射出的思维的交锋、观点的碰撞、情感的交融、经验的积累、思想的领悟，构筑起更加丰富多彩的学习时空。而这，恰恰正是我们更加需要的境界。

从最初的基于理解到后来的基于探索，再到最后的基于创造，学习空间的不断敞开，彰显着我们对学生的信任，更彰显着我们对学习的一种正确理解和把握。而不同的问题呈现，恰恰折射出不同的教学路径，最后，殊途殊归，自然也是情理之中的事情了。

江苏南京市北京东路小学）