三值自由模态逻辑FML

2016-06-17胡泽洪邓雄雁

华南师范大学学报（社会科学版） 2016年1期

胡泽洪，邓雄雁

三值自由模态逻辑FML

胡泽洪，邓雄雁

【摘要】FML是以自由逻辑为基础构建起来的一个三值模态谓词逻辑表列系统。若一个词项无所指(空词项)则包含该词项的简单句子无所指(即无真值)，FML的偏函数语义模型体现了这一思想。通过借鉴普利斯特的一度衍推系统和菲汀的抽象谓词思想，FML系统刻画了在内涵语境下关于空词项的推理规律。最后，用数模的方法证明了FML的强完全性。

【关键词】空词项一度衍推抽象谓词模态逻辑

在日常交流和推理中，我们允许名称词项t指称不存在个体，诸如此类的词项称为“空词项”(empty term)。例如，词项“孙悟空”。包含空词项的推理大量存在于日常生活中，而这恰是一阶逻辑和以一阶逻辑为基础的模态谓词逻辑的短板。[1]自由逻辑是一种处理空词项的逻辑，在自由逻辑的基础上加入模态算子可构成自由模态逻辑。这种逻辑可以在模态语境下对空词项进行逻辑分析，进而刻画内涵语境下关于空词项的推理规律。

自由逻辑的语义要考虑如何给包含空词项的基本闭公式Pt赋值(基本公式是指不含命题联结词和量词的公式)。包含空词项的基本公式赋值有三种可能：其一，该公式为真；其二，该公式为假；其三，该公式不真也不假(也可称为无真值)。按此线索，可以把自由逻辑分为三类：负自由逻辑，正自由逻辑，中性自由逻辑。中性自由逻辑是自由逻辑并且使得任一包含有空词项的基本公式(可能除“t存在”外)都无真值。[2]2—3可见，中性自由逻辑的语义是一种三值逻辑语义。莱曼于1994年构建了一个中性自由逻辑表列系统(tableaux)。[3]本文对莱曼的语义模型做了一些调整，以勒布兰克的偏函数语义模型[4]为基础而设计了一个中性自由模态逻辑语义模型。在语形上，以普莱斯特的一度衍推(First degree entailment)系统[5]为基础建立了一个三值自由模态逻辑表列系统FML。为了便于区分模态公式的从言和从物命题，还在FML中加入一个特殊的谓词，那就是菲汀提出的谓词抽象理论。[6]

一、FML的语法和语义

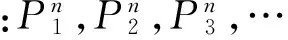
(2)逻辑符号：(a)变元，连接词，量词，模态词如常。(b)逻辑谓词：=，ε。

(3)辅助符：)，(。

我们常用a，b，c，…表示常元;x，y，z，…表示变元；P，Q，O，… 表示n元谓词;ε是特殊的谓词，称为存在谓词。严格指示词是指名称所指称的对象不随可能世界变化而变化，反之为非严格指示词。[7]项t的形成规则如常，公式形成规则如下：

(1)原子公式形成规则如常，复合公式形成规则如常。

(2)若t是项，那么εt是公式。

(3)若A是公式，t是任一项，〈λx.A〉是一抽象谓词，那么〈λx.A〉(t)是公式；

FML的语义以克里普克可能世界语义理论为基础，结合偏函数语义理论而构成[4]。

定义1框架F=〈W,R,D〉,

(2)R是W上的二元关系使得R⊆W×W；

(3)D是域函数，对任ωW，映射ω到一非空集 Dω。

若框架F=〈W,R,D〉，则框架上的域 D(W)=U{Dω|ωW}。(在不引起混淆的情况下，把D(W)简写为D)在这里，可能世界是变化的，也就是说量词的论域是随着可能世界变化而变化的，所以这个模型又称为变域模型[8]101-105，与之对应的是常域模型。

(1)对任一常元c，c是严格指示词，若 I(c)在ω处有定义，则I(c)Dω；

(2)对任一常元τ，τ是非严格指示词，若 I(τ)ω在ω处有定义，则I(τ)Dω；

(3)对任一变元x，若σ(x)在ω处有定义，则σ(x)Dω；

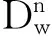
(1)若对任ti(1≤i≤n)，I(ti)ω有定义，则：

(a)Vσ(Pt1t2…tn)=1，当且仅当〈I(t1)ω，…，I(tn)ω〉I(P)ω；

(b)Vσ(Pt1t2…tn)=0，当且仅当〈I(t1)ω，…，I(tn)ω〉∉I(P)ω。

(2)对某一 ti(1≤i≤n)，若I(ti)ω无定义，则Vσ(Pt1t2…tn)ω=*；(*代表“第三值”，也可以理解为“无真值”)

我们对存在公式εt作了特殊处理，使之只有真、假两个值。复合公式按强Kleene-3 真值表进行赋值，强Kleene-3 真值表如下：

┐→1*01011*0***1**010111

定义4对量词公式、模态公式和抽象谓词公式的赋值[6]如下：

(1)对公式∀xA：

(c)否则，Vσ(∀xA)ω=*

(3)对谓词抽象公式〈λx.A〉(t)：

(c)否则，Vσ(〈λx.A〉(t))ω=*

可满足，有效，语义后承定义如常，不再一一列出。

二、表列系统FML

在普利斯特所介绍的一度衍推系统[5]329—347基础上引入谓词抽象规则[6]171-193形成表列系统FML。一个表列是一个结构图，形状如下：

一表列结构(也叫做树)就是一个拥有唯一极大元x0的偏序结构，使得对任一表列中的元素 xn，总存在唯一有穷元素链 xn≤xn-1≤x1≤x0。上图中每个点叫节点，最顶端的节点叫根，最底端的节点叫端点，由箭头所标示的由根到端点的节点序列称为表列的枝。一个表列可同时有多条枝，也可只有一条枝。

为了验证一个FML推理的有效性，只需建立一个表列，使得根上同时有这个推理的前提和结论的否定(不真，也称为初始列)，再按照表列扩展规则把初始列加以展开，形成不同枝。FML树规则如下。

(一)命题连接词规则

1.(A→B，+i)⊃(A，+i)▽(B，+i)

2.(A→B，-i)⊃(A，-i)△(B，-i)

其中， i代表标号，可以理解为一个可能世界；“▽”是元语言符号，表示“或者”的意思，在表列上，意味着分叉;“△”表示“并且”的意思;“⊃”表示“推导”的意思，在表列上，意味着箭头。

(二)量词规则

(UI+)、(∀xA，+i)△ (εa，+i)，⊃(A(a/x)，+i)；(PI-)、(∀xA，-i)⊃(εc，+i)△(A(c/x)，-i)；(PI+)、(∀xA，+i)⊃(εc，+i)△ (A(c/x)，+i)；(UI-)、(∀xA，-i)△ (εa，+i)⊃(A(a/x)，-i)

UI±中a是在枝上已经出现的任一严格指示词；PI±中c是枝上尚未出现的新严格指示词。

(三)模态词规则

(□+)、(□A，+j) △(irj)⊃(A，+j)；(□-)、(□A，-i)△ (irj)⊃(A，-j)；(◇+)、(□A，+i)⊃(irj)△(A，+j)；(◇-)、(□A，-i)⊃(irj)△ (A，-j)

其中，□±中j是树上已经存在的标号；◇±规则中的j是尚未在树上出现的新标号。irj表示可能世界i和j具有通达关系r。

(四)等词规则

( IE′)、(εc，+i)⊃(c=c，+i)；(SI′)、(a=b，+i)△(A(a/x)，+i)⊃(A(b/x)，+i)

(五)特征规则

(ⅡR′) 、(a=b，+i)△ (εa，εb，+j)⊃(a=b，+j)；(DI′)、(ετ，+i)⊃(c=τ，i)；(NCR+)、(Pc1…cn，+i)⊃(εcn，+i)；(NCR-)、(Pc1…cn，+i)⊃(εc1，…，εcn，…εc1，+i)

其中 NCR±要求Pc1…cn为基本公式，ⅡR′中a和b均为严格指示词，亦即必然同一规则。也就是说，一旦两个严格指示词相等，则必然相等。因而，FML是一个必然等同模态系统。

(六) 附加规则

1.(εa，…，εb，+i)△(Pc1…cn，-i)⊃(Pc1…cn，+i)

2.(εa，…，εb，+i)△(Pc1…cn，-i)⊃(Pc1…cn，+i)

(七)抽象谓词规则

1.(〈λx.Ax〉(t)，+i)⊃(A(tσi⊃)，+i)△(εt，+i)

3.(〈λx.Ax〉(t)，-i)△(εt，+i)⊃(A(tσi)，-i)

其中，t是任一项，我们规定：如果t是严格指示词c，则tσi为c；如果t是非严格指示词τ，则tσi为由DI′规则所得到的第一个新严格指示词c。这可保证无论在那种情况下tσi都是严格指示词。

直觉上，树中节点上A，+i表示在i中A为真，A，-i表示在i中A不真。为了验证A1，A2，…，An┠B，只需构造一个包含如下公式序列为初始列的表列即可。这个初始列即 A1+i，A2+i，…，An+i，B-i。针对每一组公式都可由表列规则进行扩展，直到每个端点(除UI±外)不能再使用扩展规则进行扩展，这样可以构成一个完全的表列或闭树，这个表列就是对A1，A2，…，An┠B的一个FML推导。由上述树规则形成的表列系统称为中性自由模态逻辑FML。

定义5某一枝是FML闭枝，当且仅当枝上：

(1)同时含有公式A，+i和A，+i，或者

(2)同时含有公式 A，+i和A，-i，

(3)否则称为开枝。

定义6公式A是闭公式集Φ的FML语法后承Φ┠A ，当且仅当存在一个完全的闭树使得其初始列包含 Φ中的所有公式 B，+i和 A，-i；反之，如果该FML完全树是开树，则A不是公式集Φ的FL语法后承，记为 ΦA。

自由模态逻辑FML的一个特点是有语法后承但不一定有相应的内定理。例如，在FML中，有Pc┠∃xPx，但Pc→∃xPx，验证从略。再如，在菲汀的二值模态逻辑系统中有：〈λxy.(x=y)(s，t)┠〈λxy.(□x=y)〉(s，t)[8]226，即我们把项之间的相等作从物模态理解，则它们是必然相等的。但在FML中有，〈λxy.(x=y)(s，t)〈λxy.(□x=y)〉(s，t)。现构造树如下：

1.〈λxy.(x=y)〉(s，t)+1

2.〈λxy.(□x=y)〉(s，t)-1

↓

3.εsσ1，εtσ1+1

4.sσ1=tσ1+1

5.□sσ1=tσ1-1

6.1r1.1

7.sσ1=tσ1-1.1

其中，左边的数字表示扩展顺序，右边的数字表示可能世界的标号。1，2构成初始列。3， 4自1，5自2，3，分别运用了抽象谓词规则；6和7自5，运用了模态词规则；这个树没有封闭，可知，〈λxy.(x=y)〉〈λxy.(□x=y)〉(s，t)。

引入抽象谓词，可以对模态从言和物命题进行有效区分，增强一阶模态语言的表达能力；从而对内涵语境中相等问题即“弗雷格之谜”[8]142-144，进行很好地区分和分析；还可以对蒯因对模态逻辑特别是模态谓词逻辑的合法性的质疑[9]150-171进行反驳。

三、FML的可靠性和完全性

自由模态逻辑必然同一系统FML相对于中性偏函数语义具有可靠性和完全性。需要先证明协同引理和代入引理。

证明：对公式A进行结构归纳证明，略。

代入引理在模态谓词逻辑中不一定成立。为此，需要对代入引理作一些调整，我们规定代入项只能为严格指示词。

引理2 (代入)在模型M中，对至多只有一个自由变元x的公式A，如果对任一严格指示词c，V(c)在ω处有定义，且存在dD，使得 V(c)=Vσ(d/x)(x)，则对任ωW，

证明：当A中不含自由变元x，由协同引理，易见V(A(c/x))ω=V(A)ω=Vσ(d/x)(A)ω。当A中含自由变元x，对公式A进行结构归纳：

情况二A为公式〈λy.B〉(t)

(1)x为 y，(〈λy.B〉(t)(c/x)=〈λy.B〉(t(c/x))

(b)V(〈λy.B〉)(t(c/x))ω= 0情况类似，略。

(2)x不为y

(a)V((〈λy.B〉(t)(c/x))ω=1

(b)V((〈λy.B〉(t)(c/x))ω=0，类似，略。得证。

(1)对B每一节点，若A，+i在节点上，则A在f(i)W中为真；若A，-i在节点上，则A在f(i)W中不真。

(2)若irj在B中，则在M中有f(i)Rf(j)。

证明：逐个验证连接词规则、量词规则、等词规则和附加规则即可，略。

可靠性定理在偏函数语义条件下，对FML任一有穷闭公式集Φ和闭公式 A，如果Φ┠A,则ΦA。

现在来考虑完全性问题，FML相对于中性偏函数语义具有强完全性。在这里给出的是表列系统而非公理系统，我们用树模进行完全性证明，而不是用公理系统典范模型来证明。[10]

(6)对一 n元谓词P，严格指示词ci(1≤i≤n),〈[c1],[c2],…[cn]当且仅当 Pc1c2…cn+i在B中；〈[c1],[c2]…，[cn]〉∉当且仅当┐Pc1c2…,+i在B中；否则V(Pc1c2…cn)=*。

引理4(完全性) 对任一FML开树B，存在一树模M使得对B中任一闭公式A ：

证明：施结构归纳于A。

情况一A为εt，略。

情况二A为a=b

(1)a=b,+i在B中，略；

(2)┐(a=b),+i在B中，

(3) a=b,-i在B中，

(a)εa，+i和εb，+i均在B中，

(b)εa，+i和εb，+i至少有一个不在B中，

综合(a)和(b)，可知，并非V(a=b)=1；

(4)┐(a=b) ，-i在B中，

(a)εa，+i和εb，+i均在B中，

(b)εa,+i和εb，+i至少有一个不在 B中，

综合(a)和(b)，可知，并非V(a=b)=0；

情况三A为原子公式Pc1c2…cn，┐B,B→C,∀xB，略。

情况四A为〈 λx.B〉(t)，

(2)〈λx.B〉(t),-,i在B中，则

(a)εt,+i在B中，

(b)εt,+i不在B中

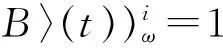
(3)其他两种情况类似，略去。

完全性定理相对于中性偏函数语义，对任一个FML闭公式集Φ和闭公式A，如果ΦA，则ΦA。

证明：假设ΦA，则存在一完全开树B，可构造一树模 M，据完全性引理，M使得Φ中所有公式为真且A不真，即ΦA。

由完全性证明可以知道，这个证明要比典范模型方法简洁，其过程没有极大一致集构造等步骤，从而简化了证明过程。FML系统有语法后承，但可能会无相应的内定理，所以难以证明其弱完全性定理，即若A，则A不一定成立。

在FML中，从多值内涵语境中考察空词项的逻辑特性，其最大特点是运用了谓词抽象这一工具。它有效区分了从言和从物模态，并且仔细区分了严格指示词和非严格指示词的语义特性，并在语形方面进行了对比。此处所构造的系统为必然等同系统，即承认推理规则IIR′。当然，在模态谓词逻辑中，有不认可必然等同的系统，这就是模态逻辑的偶然等同系统。偶然等同系统相对于必然等同系统，在语形上去掉IIR′即可，不过其语义相对复杂，因为，要把存在域处理为具有函数形式的内涵对象，至于内涵对象是否可行，尚存在争议。

参考文献：

[1]胡泽洪，邓雄雁．论模态谓词逻辑的“非指称”问题──基于自由逻辑的考察．哲学研究，2011(2)：101—106.

[2]M.MORSCHER, A.HIEKE. ( ed.). New Essays in Free Logic: In Honour of Karel Lambert (Applied Logic Series, vol. 23).Dordrecht: Kluwer, 2001.

[3]C.LEHMANN.StrictFregeanfreelogic. Journal of Philosophical Logic ,1994(23):307—336.

[4]H.LEBLANC, K.MEYER ROBERT.OnPrefacing((X) (A(Y/X)with(∀Y),AFreeQuantificationTheorywithoutIdentity. Zeitschrift füe mathematische Logik und Grundlagen der Mathematik ,1970(16):447—462

[5]G.PRIEST. An introduction to Non-Classical Logic. Cambridge : Cambridge University Press, 2008.

[6]M. C.FITTING.First-Orderintensionallogic. Annals of pure and applied logic,2004(127):171—193.

[7][美]克里普克．命名和必然性. 梅文，译，上海：上海译文出版社, 1988.

[8]M. C.FITTING, R. L.MENDELSOHN. First-Order Modal Logic. Dordrecht: Kluwer, 1998.

[9][美]蒯因．从逻辑的观点看．陈启伟，江天骥等，译，北京：中国人民大学出版社，2007．

[10]邓雄雁，胡泽洪．协调、一致与一阶公理系统的强完全性．华南师范大学学报：社会科学版，2010(3)：112—116.

【责任编辑：赵小华】

【基金项目】国家社会科学基金项目“自由逻辑及其相关哲学问题研究”(13BZX068)

【收稿日期】2015-08-10

【中图分类号】B81-0

【文献标识码】A

【文章编号】1000-5455(2016)01-0176-06