公路桥梁车辆行驶间距研究*

王强　苏成

(华南理工大学 土木与交通学院， 广东 广州 510640)

公路桥梁车辆行驶间距研究*

王强苏成

(华南理工大学 土木与交通学院， 广东 广州 510640)

摘要：利用一维随机更新计数场描述公路桥梁上行驶着的车辆，推导得到一般运行状态下车辆行驶间距服从指数分布的性质，并利用动态称重系统实测的大量自然行驶的车辆间距对其进行了验证，认为该性质可用于桥梁的交通量适应性评价.将实测车辆以时间间隔3 s为界划分为一般运行状态和密集运行状态，对比分析了其时间间隔和行驶间距的统计结果与我国规范修订时的调查统计结果的差异，认为以3 s为界的时间间隔不能完全划分车辆的运行状态，应以车辆的行驶间距进行划分.对比实测自然行驶车辆行驶间距的概率分布特征和一般运行状态下车辆行驶间距的理论概率分布特征发现：行驶间距小于44.35 m时车辆处于密集运行状态，通过多项式回归得到其概率分布；行驶间距大于44.35 m时为一般运行状态，其概率分布为指数分布.这些特征可用于建立公路桥梁多参数随机车辆荷载模型.

关键词：公路桥梁；行驶间距；一维随机更新计数场；指数分布；多项式回归；一般运行状态；密集运行状态

公路桥梁上车辆作用所产生的车辆荷载效应是桥梁承载能力计算、评估分析乃至寿命预测等各种研究的重要依据之一.由于公路桥梁上的车辆具有较强的随机性，仅按设计标准给出的车辆荷载不能反映桥梁的真实车辆荷载效应，需要建立与桥上实际交通荷载状况相适应的车辆随机荷载模型，才能得到满足实际桥梁分析需要的真实荷载效应.桥梁的车辆荷载效应除了与车辆自身的轮轴重和轮轴间距等参数有关外，还与车辆之间的行驶间距密切相关，不同间距的车辆作用在桥梁上所产生的车辆荷载效应是不同的.

近年来，随着对车辆荷载模型研究的不断深入，尤其是对车辆调查手段和能力的提高，车辆荷载模型从以车辆统计数据为基础的确定性模型研究转变为基于概率和随机理论的多参数随机车辆荷载模型研究[1].这是公路桥梁荷载研究的新阶段.目前虽然有一些研究成果，但还很少做到车辆荷载全参数的随机仿真模拟.其中车辆行驶间距是进行多参数随机模拟的重要参数，建立与实际交通荷载状况相适应的车辆荷载模型，以准确有效地进行桥梁各种分析评估[2]，大部份的研究是以车速度和间距不变为基础.可见，准确把握车辆行驶间距的客观规律十分必要.

对车辆行驶间距的研究多在交通控制领域，以交通流理论和车辆运动特性为基础，多采用概率论、流体力学和动力学等方法分析车辆之间的安全跟驰距离[2].自1950年Reuschel用跟驰理论进行研究以来，学者们先后提出了诸多模型[3-9](如Netsim模型、Fresim模型、Intras模型和Carsim模型等)来研究车辆行驶过程中车辆状态等因素与跟驰距离的关系.

近年来，随着动态称重系统(WIM)的发展，对公路上通行车辆进行调查的能力得到提高，获得了越来越多的车辆轴重、轴距、速度和通行时刻等观测资料，对车辆行驶距离的研究也逐步深入.各研究者对各自的观测资料进行统计分析，提出了相应的车辆行驶间距概率模型.国外多以车辆时间间隔的统计结果为研究对象，提出了移位指数分布、均匀分布、Gamma分布[10]、分段抛物线[11]等概率模型.中国现行公路桥梁设计规范修订时[12-13]，根据4条国道上的观测资料，以3 s为界将车辆划分为一般运行状态和密集运行状态，提出了车辆时间间隔的Gamma模型和车间距的对数正态模型.其他研究者也提出了车辆间距的统计模型：王硕[14]和安振源[15]提出了对数正态模型，冯兆祥等[16]提出了Possion模型，陈攀[17]提出了Pearson-Ⅵ型模型和Pearson-Ⅰ型模型，孙吉书等[18]提出了Pearson-Ⅲ型模型等.

在桥梁车辆荷载领域对车辆行驶间距的研究成果都是基于实测调查的基础上的统计分析，但由于研究者进行调查的对象和样本的不同，所得到的统计模型也不同.尚未从理论上阐释车辆行驶间距的本质特征，对车辆行驶间距的客观规律缺乏统一认识.

在进行车辆荷载随机模拟时，对车辆运行状态的划分一直沿用中国规范修订时给出的车辆时间间隔是否超过3 s的标准，将车辆划分为一般运行状态和密集运行状态[13]的划分方法.这种方法是在过去对车辆调查信息不够充分的基础上提出的，具有一定的局限性.有必要重新审视这种划分方法的合理性.

文中首先基于一维泊松随机场理论推导得到在一般运行状态下车辆行驶间距的理论概率分布性质，并利用实测数据的统计结果对该性质进行了验证.然后从车辆的时间间隔和行驶间距两方面分别与中国规范修订时的统计结果进行对比，并进一步对比实测自然运行情况下车辆行驶间距的概率分布和一般运行状态下车辆行驶间距的理论概率分布，拟合分析得到车辆在一般运行状态和密集运行状态下的行驶间距概率分布.文中结论可为公路桥梁车辆荷载多参数随机模型的研究提供基础.

1车辆行驶间距的理论概率分布

1.1桥上车辆数量的概率分布

桥上出现车辆的过程可采用随机过程理论来描述[13,19].如果将随机过程研究的时间域转移到空间域上便是随机场，其便能在工程中成为分析结构空间上随机参数特性的有效工具[20-21].如果空间域为一维空间L，则为一维随机场，随机过程的各种性质可以类似地用到随机场上.

对于自由行驶在公路桥梁上的处于一般运行状态的车辆，可用图1和式(1)来描述其在桥上的分布，记随机事件A为

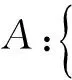
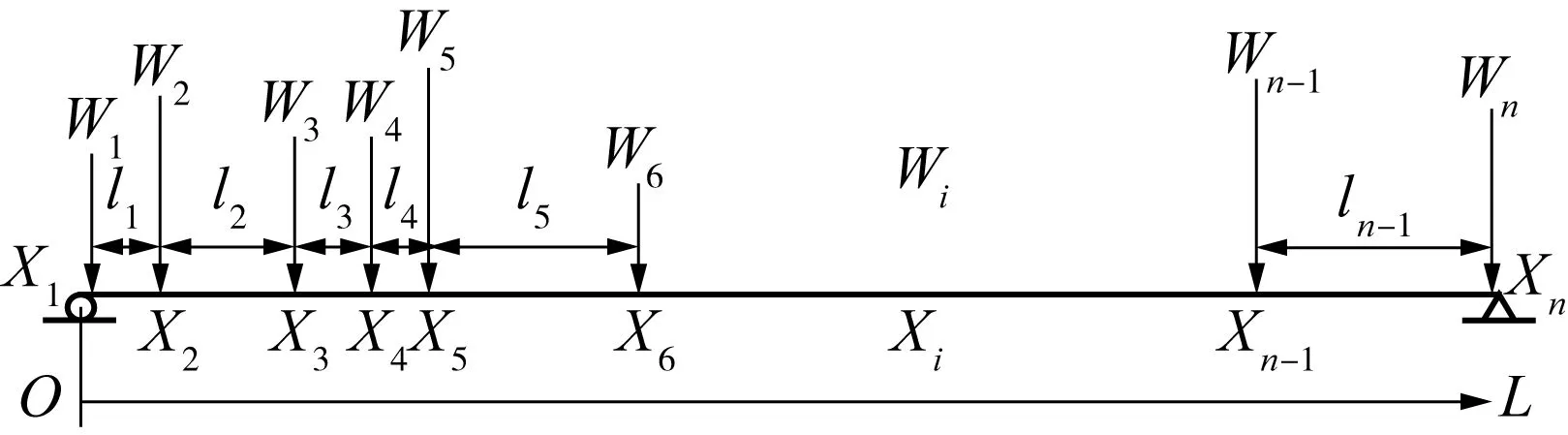
图1　桥上车辆的随机分布Fig.1　Random vehicles scattering on bridge

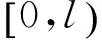
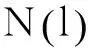
(3)在任意充分短的距离范围内，最多只有一部车辆的存在，否则会出现车辆碰撞事件.

(2)

1.2车辆行驶间距的理论概率分布

(3)

式中，F为概率分布函数.

可见，一般运行状态下自由行驶在公路桥梁上的车辆的行驶间距服从指数分布.

2一般运行状态下车辆行驶间距理论概率分布的验证

2.1车辆信息采集

为验证式(3)，利用能够实时不间断采集的动态称重系统WIM，在无人值守情况下获得实际公路上不受任何外在人为干扰的自然行驶状态下的车辆信息.由多套动态称重系统经标定后在107国道(G107)、京港澳高速公路(G4)、京珠高速公路(G4w)、虎门大桥(G9411)、沈海高速公路(G15)、虎门渡口东引道(S358)等多条公路上采集，累计历时400多天，共获得逾2 400万余部车辆的信息[23].

2.2车辆行驶间距的计算

由各路段上所埋设的车辆动态称重系统所记录的车辆通过时的时刻、速度和轴距等信息得到车辆的行驶间距.

以各动态称重系统开始采集的某时刻开始，连续记录得车辆队列，由于前后车辆出现时间间隔较短，可以认为在后一部车辆到达之前，前一部车辆以均匀速度行驶.这样，由前一部车辆的速度vi和时刻ti，与后一部车辆出现的时刻ti+1，便得到前后车辆的车头间距：

(4)

车头间距扣除由前一车辆各轴距之和构成的车辆长度di，便得到后一车辆与前一车辆之间的车辆行驶间距，为同向行驶连续2辆车辆的前车后轴与后车前轴之间的间距，即

(5)

2.3车辆行驶间距的概率分布

图2　车辆车头间距和行驶间距概率分布曲线Fig.2　Probability distribution curves of spachead way and travel spacing of vehicles

进一步分析可知，当车辆为自由行驶即处于一般运行状态时，后车的行驶不受其与前车之间距离的制约，自由地以各种速度和加速度行驶，显然此时车辆队列是疏松的.反之，后车辆与前车之间因距离不足而产生制动时，车辆队列是紧密的，称车辆处于密集运行状态.显然，当桥上车辆处于一般运行状态时，桥上的交通是通畅的，桥梁可以适应桥上的交通量状况.因而，可以根据桥上车辆是否为一般运行状态，即桥上车辆的行驶间距是否为指数分布，来进行桥梁对交通量适应性的评价.

3车辆行驶间距的对比分析

中国现行公路桥梁设计标准修订时，采用人工为主的方法对车辆进行调查得到的一般运行状态和密集运行状态车辆的时间间隔和车间距的概率分布及其参数见文献[12]，如表1所示.

随着WIM的发展，采用自动、无人值守的车辆自动调查技术，获得大量不受干扰情况下车辆自然运行的客观信息成为可能，对车辆实测调查统计的结果更加符合实际公路上车辆的行驶状况.文中的调查技术及方式、调查路段的路况，以及调查样本量等与文献[12]存在较大差异，再加之车辆性能的发展，使得笔者的统计结果与表1的统计结果有较大差异.为便于对比，仍按表1的划分方法，以3 s为界分别进行统计结果的对比.

表1车辆间隔概率分布及其参数[12]

Table 1Probability distribution types and their parameters of spachead way and time interval of vehicles[12]

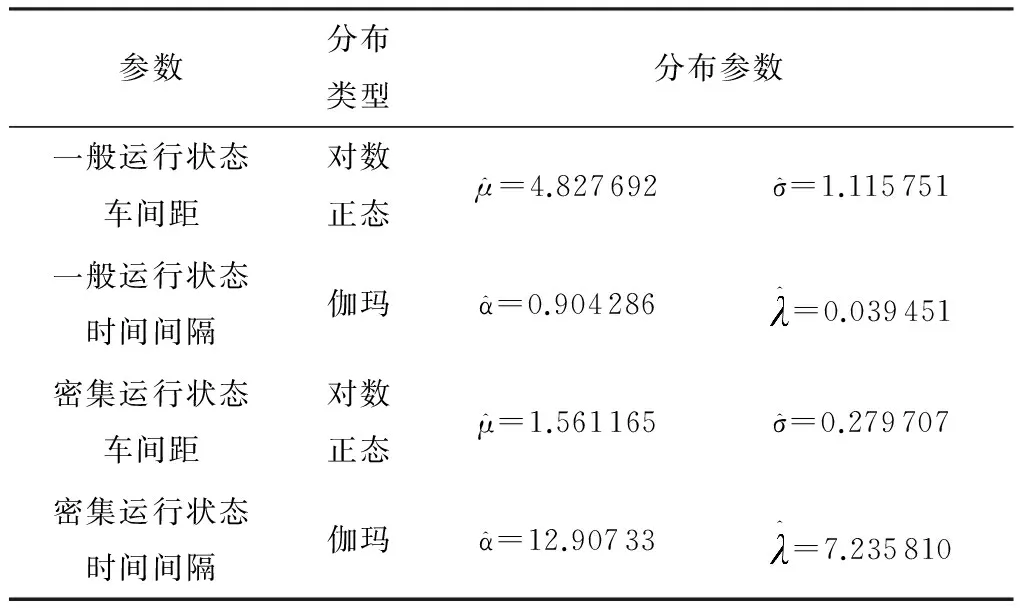
参数分布类型分布参数一般运行状态车间距对数正态μ^=4.827692σ^=1.115751一般运行状态时间间隔伽玛α^=0.904286^=0.039451密集运行状态车间距对数正态μ^=1.561165σ^=0.279707密集运行状态时间间隔伽玛α^=12.90733^=7.235810

3.1车辆的时间间隔

图3为3 s以下的实测车辆时间间隔概率密度f及概率分布P的统计曲线和表1的统计曲线的对比图.两者不但在分布类型上存在差异，在概率分布上也不同，在时间间隔较小时实测车辆出现的概率相对较大，而时间间隔较大时实测车辆出现的概率相对较小.

图3　3 s以下车辆时间间隔的统计结果Fig.3　Statistical results of time interval of vehicles within 3s of time interval

图4为3 s以上的实测车辆时间间隔统计曲线和表1的统计曲线的对比图.虽然两者的概率分布类型相似，但实测曲线较陡，分布范围较窄，集中分布在50 s以内，而表1的统计曲线相对较缓且分布范围较宽，大部分车辆的时间间隔在100 s以内.

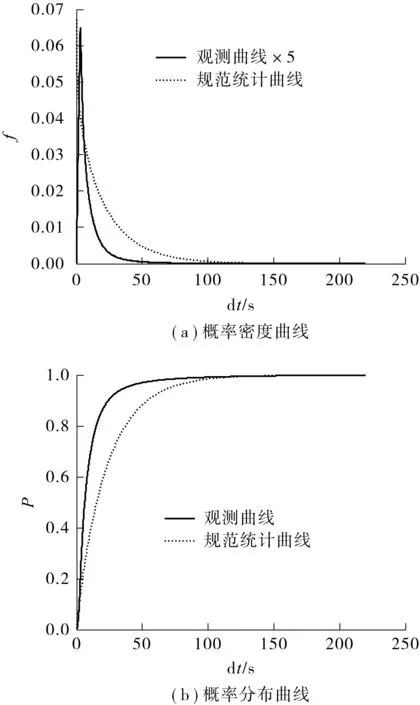
图4　3s以上车辆时间间隔的统计结果对比Fig.4　Statistical results of of time interval of vehicles over 3s of time interval

3.2车辆的行驶间距

图5为车辆时间间隔在3 s以下时实际车辆行驶间距统计曲线与表1的统计曲线的对比图.实际的车辆行驶间距分布在0～80 m范围，而表1的统计曲线集中分布在0～10 m范围内.结合实际公路上车辆行驶情况，实际观测得到的分布范围较为合理.

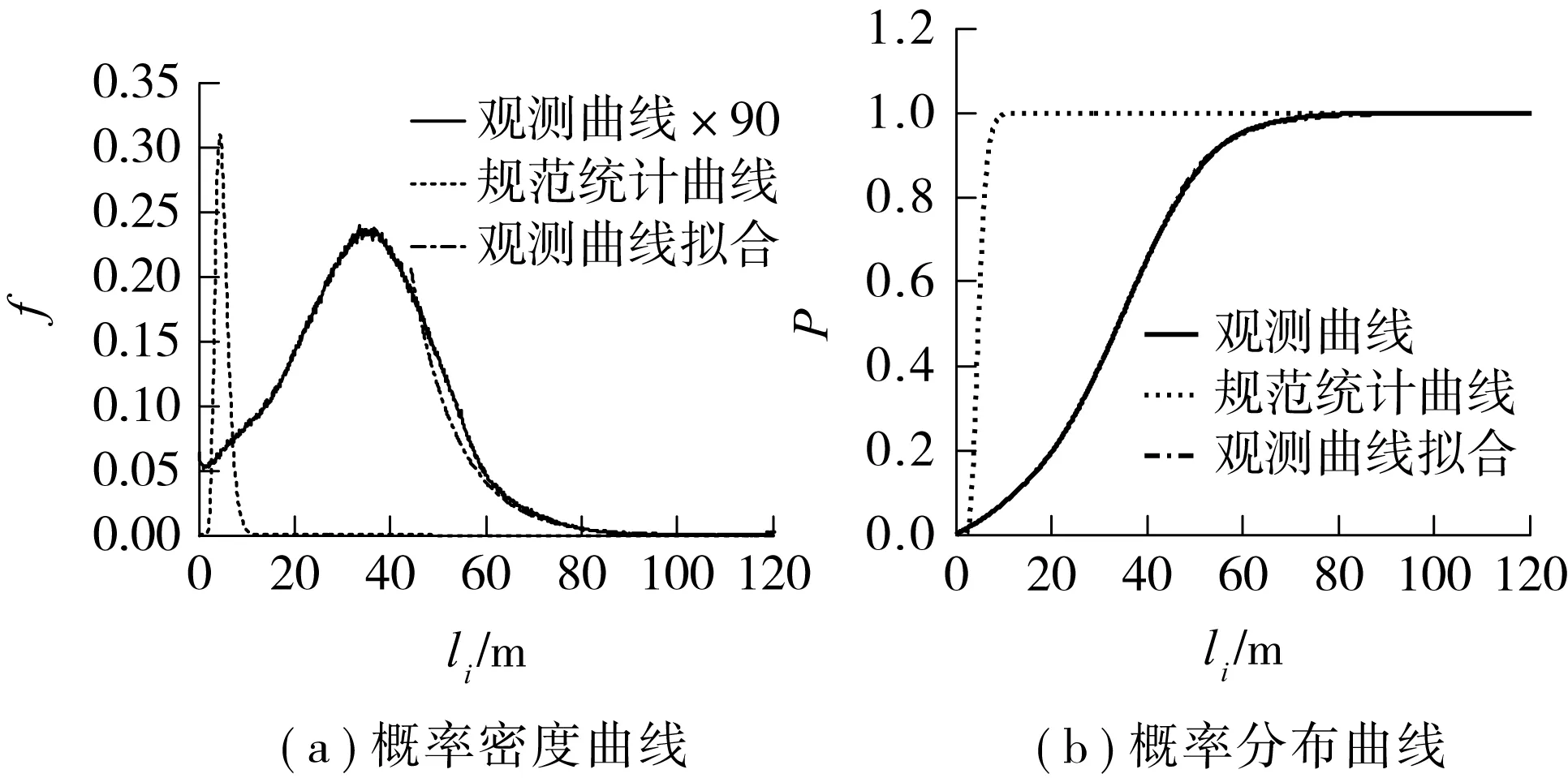
图5　3s以下车辆行驶间距统计结果Fig.5　Statistical results of travel spacings of vehicles within 3s of time interval

图6为车辆时间间隔在3 s以上时实际车辆行驶间距统计曲线与表1统计曲线的对比图.虽然两者分布类型相近，但从概率分布曲线上看，行驶间距在常见的0～400 m范围内，同一概率分位值点处的实际车辆行驶间距大于表1的统计结果，表明实际公路上3 s以上的车辆其行驶间距大于规范修订时的统计结果，这与实际公路高速行车速度较文献[12]统计时的车速高、以及这些年来车辆性能的提高有关.

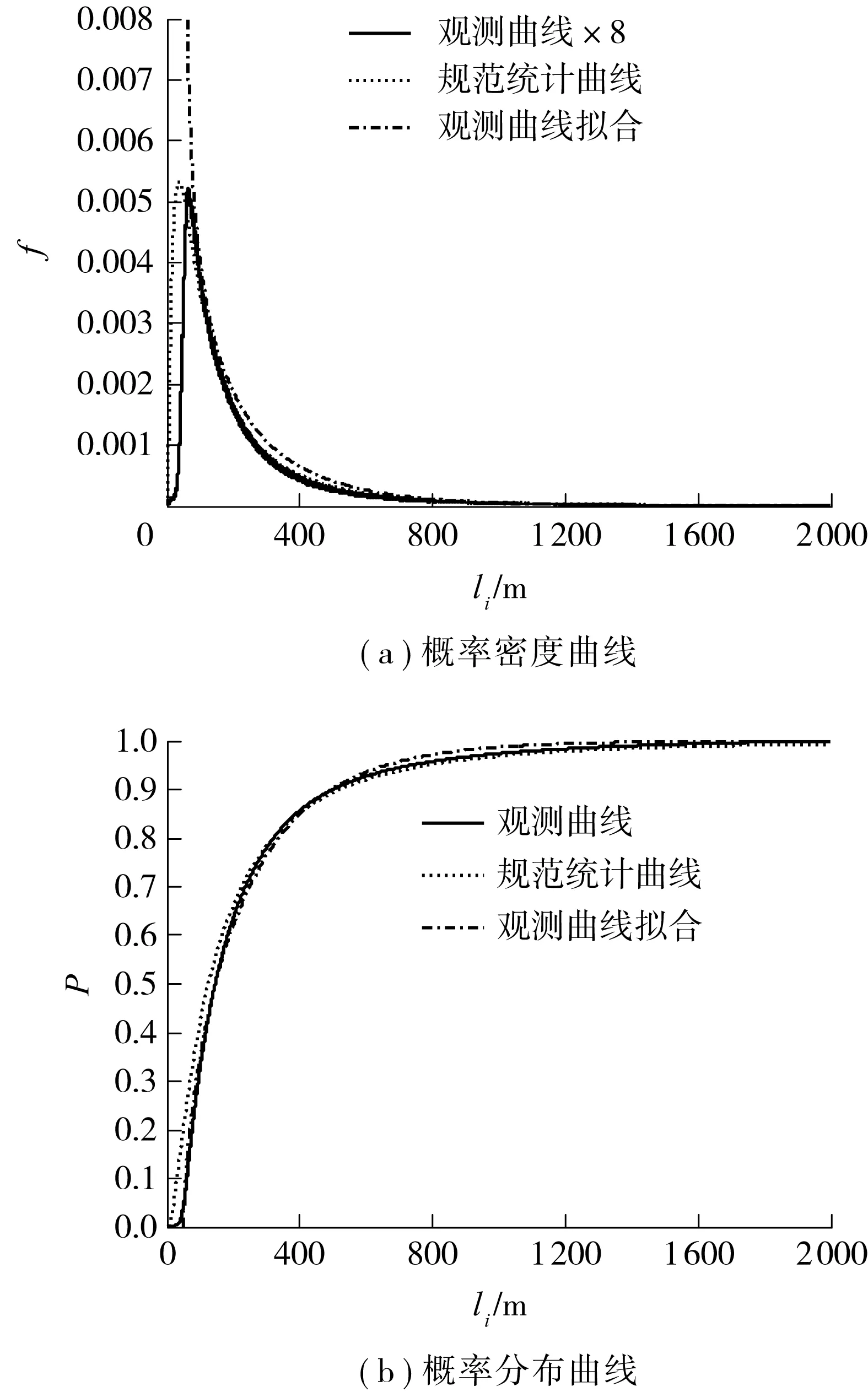
图6　3 s以上车辆行驶间距的统计结果Fig.6　Statistical results of travel spacings of vehicles over 3s of time interval

3.3以3 s为界的车辆运行状态分析

分析图5中给出的时间间隔在3 s以下时车辆行驶间距的实际观测结果的概率统计曲线可以发现，当车辆的行驶间距大于44.35 m时，车辆行驶间距的概率分布曲线可用指数分布来拟合，拟合曲线与实测曲线几乎重合.结合前述式(3)的结果说明，即使是时间间隔小于3 s的车辆，仍有部分车辆处于一般运行状态.

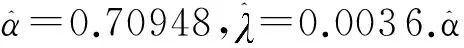
4车辆运行状态划分的建议

上述对实测车辆行驶间距的统计对比结果表明，仍有部分时间间隔在3s以下的车辆处于一般运行状态，而部分时间间隔在3s以上的车辆并非处于一般运行状态，以车辆时间间隔3s为界不能完全划分车辆的运行状态.

事实上，车辆的运行状态描述的是公路上车辆队列是密集的还是疏松的，应以前后车辆之间的行驶间距来表征，以时间间隔来表征缺乏理论依据.车辆行驶间距不仅与前后车辆的时间间隔有关，还与车辆的行驶速度密切相关，同样时间间隔的车辆其行驶间距因速度的不同而不同.从前述的理论推导结果表明，前后车辆之间的行驶间距是划分车辆运行状态的直接依据.

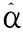
图7　车辆行驶间距的概率密度曲线Fig.7　Probability density curves of travel spacing of vehicles

对于图7中在峰值点之前的车辆行驶间距作统计分析，如图8所示，显然此时的车辆因间距较小而处于密集运行状态.采用多项式拟合能得到较好的拟合结果，其概率分布曲线为

F(l)=1.302×10-6l3+0.000 364 5l2+

0.004 013l+0.008 915，0

图8　密集运行状态车辆行驶间距概率分布曲线Fig.8　Probability distribution curves of travel spacings in dense traffic state

综上所述，应以公路上的车辆行驶间距作为划分车辆运行状态标准，当行驶间距小于44.35 m时车辆处于密集运行状态，大于此间距时车辆处于一般运行状态.

5结语

文中从理论和实测统计结果证实，车辆在一般运行状态下其行驶间距服从指数分布.研究发现， 以3 s为界的时间间隔不能完全划分车辆的运行状态，44.35 m可作为车辆密集运行状态和一般运行状态划分的界限.文中工作为车辆行驶特征一般性的统计规律描述，有必要对车辆行驶间距进一步细化分析，针对不同类型的车辆在不同行车道上的行驶间距进一步统计分析，弥补现有公路桥梁交通荷载研究的不足，为公路桥梁车辆荷载多参数随机模型的研究提供基础.

参考文献：

[1]《中国公路学报》编辑部. 中国桥梁工程学术研究综述·2014 [J]. 中国公路学报，2014，27(5)：1-96.

Editorial Department of China Journal of Highway and Transport. Review on China’s bridge engineering research:2014[J]. China Journal of Highway and Transport,2014，27(5)：1-96.

[2]王涛,韩万水,黄平明. 公路桥梁交通荷载研究现状及展望 [J]. 建筑科学与工程学报,2010,27(4):31-38.

WANG Tao,HAN Wan-shui,HUANG Ping-ming. Research status and prospect on traffic loading for highway bridge [J]. Journal of Architecture and Civil Engineering,2010,27(4):31-38.

[3]徐吉谦. 交通工程总论[M]. 北京:人民交通出版社,2005.

[4]JUN J．Understanding the variability of speed distributions under mixed traffic conditions caused by holiday traffic[J]. Transportation Research Part C,2010,18(4):599- 610．

[5]刘有军,李可,余俊,等. 四车道高速公路跟驰换道模型与参数激励 [J]. 中国公路学报,2014,27(12):96-105.LIU You-jun,LI Ke,YU Jun,et al. Car-following and lane-changjing modeling and parameteric excitation on four-lane express [J]. China Journal of Highway and Transport,2014,27(12):96-105.

[6]OSSEN S,HOOGENDOORN P. Reliability of parameter values estimated using trajectory observations [J]. Journal of the Transportation Research Board,2009,21(24):36- 44．

[7]罗霞,杜进有,霍娅敏. 车头间距分布规律的研究 [J]. 西南交通大学学报,2001,36(2):113-116.

LUO Xia,DU Jin-you,HUO Ya-min. Study on the distribution patterns of time headway of vehicles [J]. Journal of Southwest Jiaotong University,2001,36(2):113-116.

[8]王祺,李力,胡坚明,等. 不同车头间距下交通流的速度分布 [J]. 清华大学学报(自然科学版),2011,51(3):309-312.

WANG Qi,LI Li,HU Jian-ming,et al. Traffic velocity distributions for different spacings [J]. Journal of. Tsinghua University ( Science & Technology) ,2011,51(3):309-312.

[9]贾洪飞,隽志才.基于期望间距的车辆跟驰模型的建立 [J].中国公路学报,2000,13(4):86-87.

JIA Hong-fei,JUN Zhi-cai.Development of a car-fol lowing model based on desired spacing [J]. China Journal of Highway and Transport,2000,13(4):86-87.

[10]O’CONNOR A,JACOB B,OBRIEN E,et al. Report of current studies performed on normal load model of EC1-traffic loads on bridges[R]. Revue Francaise du Genie Civil,Hermes Science Publications,2001:411-434.

[11]OBRIEN EUGENE J ,CAPRANI Colin C. Headway modelling for traffic load assessment of short to medium span bridges [J].The Structural Engineer,2005,83(16):33-36.

[12]鲍卫刚. 公路桥梁车辆荷载研究[J]. 公路,1997,42(3):8-12.

BAO Wei-gang. Study on traffic load of highway bridge [J]. Highway,1997,42(3):8-12.

[13]国家质量技术监督局，中华人民共和国建设部. 公路工程结构可靠度设计统一标准：GB/T 50283-1999 [S]. 北京:中国计划出版社,1999.

[14]王硕. 桥梁运营荷载状况研究[D]. 上海:同济大学,2007.

[15]安振源. 基于实桥车辆调查的在役桥梁可靠度研究[D].西安:长安大学，2010.

[16]冯兆祥,张磊,吴冲. 泰州长江大桥钢塔疲劳计算随机车辆荷载模拟[J]. 公路交通科技,2008,25( 12):127- 131.

FENG Zhao-xiang,ZHANG Lei,WU Chong. Simulation of random vehicle load for fatigue calculation of steel pylon of Taizhou Yangtze River Bridge [J]. Journal of Highway and Transportation Research and Development,2008,25( 12) :127-131.

[17]陈攀. 高速公路桥梁收费站前拥堵车辆荷载评估[J]. 城市道桥与防洪,2012,29(6):44-48.

CHEN Pan.Assessment of traffic congestion load at expressway toll station [J]. Urban Roads Bridges & Flood Control,2012,29(6):44-48.

[18]孙吉书,杨春风,窦远明,等. 基于交通调查的重载交通公路桥梁设计车辆荷载探讨[J]. 河北工业大学学报,2009,38(1):91-95.

SUN Ji-shu,YANG Chun-feng,DOU Yuan-ming,et al. Study on the vehicle load of bridge design on heavy traffic highway based on traffic investigation [J]. Journal of Hebei University of Technology,2009,38(1):91-95.

[19]王强. 基于轮轴特征的公路桥梁荷载模型研究[D].福州：福州大学,2010.

[20]VANMARCKE Erik H. Probabilistic modeling of soil profiles[J]. Journal of the Geotechnical Engineering Division,1977,103(GT11):1227-1246.

[21]王强,刘仰韶,傅旭东，等. 砂土路基湿化变形和稳定性的可靠度分析[J]. 中国公路学报，2007，20(1)：7-12.WANG Qiang,LIU Yang-shao,FU Xu-dong,et al. Reliability analysis for wetting deformation and stability of sand soil roadbed[J].China Journal of Highway and Transport,2007,20(1):7-12.

[22]申鼎煊. 随机过程[M]. 武汉:华中理工大学出版社,1990.

[23]王强,刘仰韶.公路桥梁汽车的轮轴特征[J].公路交通科技,2013,30(11):41-52.

WANG Qiang,LIU Yang-shao. Characters of wheel axles of vehicles on highway bridge[J]. Journal of Highway and Transportation Research and Development,2013,30(11):41-52.

A Probe into Travel Spacing of Vehicles on Highway Bridges

WANGQiangSUCheng

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:By means of one-dimension renewal random counting field, the vehicles on highway bridges were described, and an exponential distribution was derived theoretically to describe the statistic characteristic of travel spacing of vehicles in normal traffic state, which was then verified by the statistic results obtained by weigh-in-motion in situ of the vehicles running naturally on highway bridges, finding that the exponential distribution property can be used to appraise the adaptability of bridges to traffic flow.Then, by taking 3 seconds as a time interval demarcation, the actually-surveyed vehicles were divided into two running states, namely normal traffic state and dense traffic state, and the difference in time interval and travel spacing of vehicles in these two running states between the statistic results obtained when revising the current bridge design code and the actual results was analyzed comparatively, finding that 3 seconds is not a suitable demarcation of vehicle running state and that travel spacing is more objective and reasonable for the demarcation.By comparing the probability distribution of the travel spacing between actual naturally vehicles on highway bridges and the theoretically-derived vehicles in normal traffic state, it is found that 44.35 m is a suitable travel spacing for the demarcation of running state.When the travel spacing is less than 44.35 m, vehicles run in dense traffic state and their probability distribution can be regressed as a polynomial function, while when the travel spacing is more than 44.35m, vehicles run in normal traffic state and the probability distribution function can be regressed as an exponential one.Such achievements help further establish a multi-parameter load model of random vehicles running on highway bridges.

Key words:highway bridge; travel spacing; one-dimension renewal random counting field; exponential distribution; polynomial regression; normal traffic state; dense traffic state

收稿日期：2015- 06- 01

*基金项目：国家自然科学基金资助项目(51078150)；交通运输部建设科技项目(2011318223390)；广东省交通厅科技项目(科技-2009- 01- 001- 05)

Foundation items: Supported by the National Natural Science Foundation of China(51078150) and Infrastructure Science and Technology Project of Ministry of Transport of China(2011318223390)

作者简介：王强(1973-)，男，博士后，广东华路交通科技有限公司高级工程师，主要从事路桥检测评估研究.E-mail：wq2351@163.com

中图分类号：U441+.2

doi：10.3969/j.issn.1000-565X.2016.03.014