性能需求驱动的电动汽车动力系统参数优化*

熊会元　吴小丽　宗志坚　于丽敏

(1.中山大学 工学院， 广东 广州 510006； 2.东莞中山大学研究院， 广东 东莞 523808)

性能需求驱动的电动汽车动力系统参数优化*

熊会元1,2吴小丽1宗志坚1,2于丽敏1

(1.中山大学 工学院， 广东 广州 510006； 2.东莞中山大学研究院， 广东 东莞 523808)

摘要：为有效提高电动汽车的综合性能,提出了一种基于质量功能展开和正交试验法的动力系统参数综合设计与优化方法.首先,基于质量功能展开建立了满足顾客需求的车辆性能与技术特性的耦合模型,应用粗糙数和灰色关联法确定各技术特性的加权因子;然后,基于正交试验法,以车辆综合性能最优为目标构建了动力系统参数优化设计模型,应用灰色关联法获得车辆综合性能指标系数,进而确定最优解,并对各因素进行灵敏度分析;最后,基于Matlab平台建立了电动汽车动力系统参数的设计优化模型,并以某款电动汽车为实例进行了仿真优化.仿真结果表明,优化后的车辆综合性能提升了32.3%,证明了文中方法的有效性.

关键词：电动汽车；质量功能展开；正交试验法；灵敏度分析；灰色关联法

动力系统(驱动电机、动力电池和传动系)是电动汽车的核心系统,其参数的合理设计对满足车辆动力性和经济性等综合性能具有十分重要的作用[1].动力系统参数设计与优化可分为3个层次:①对动力系统参数进行匹配计算[2-3],即根据车辆设计目标性能对动力系统所需功率、扭矩、转速及能量需求进行计算;②对动力系统某部件的参数进行优化设计,通常以能耗最低为目标来实现对目标参数的优化,如传动系速比及换挡规律的优化[4-5]、电机恒功率扩大系数的优化[6],但它们没有考虑不同部件参数间的耦合关系及其对其他性能的影响;③以动力系统的主要参数为优化参数进行多目标优化,文献[7]的优化结果为Pareto最优解集,没有确定最优解的方法,文献[8-9]引入了加权因子来获得最优解,但其加权因子的获取未能体现电动汽车的市场性能需求.

文中以电动汽车市场性能需求为驱动,以动力系统综合性能最优为目标,提出了电动汽车动力系统参数设计与综合优化方法.质量功能展开(QFD) 是在产品开发中直接面向顾客需求的方法[10],文中基于QFD建立了车辆性能与技术特性的耦合模型,用灰色关联法确定顾客需求的车辆性能与技术特性之间的关系,用粗糙数[11]客观处理顾客需求重要度;基于正交试验法,以综合性能最优为目标对动力系统参数进行优化,并分析参数间的耦合关系及其对性能指标的影响规律和灵敏度,进而获得最优解.

1基于QFD的电动汽车技术特性重要度确定方法

车辆技术特性的权重分配将决定多目标优化的结果,是体现车辆综合性能的重要组成部分,因此技术特性加权因子的获取意义重大.文中首先基于QFD建立顾客需求的车辆性能与技术特性的耦合模型,通过对顾客需求、市场竞争性和技术竞争性的分析,根据耦合模型获得技术特性的权重.

1.1车辆性能和技术特性的耦合模型

记电动汽车顾客需求的车辆性能为CR={动力性能好,使用费用低,购买价格低,续驶里程长},动力系统的技术特性即动力性、经济性指标及成本特性指标为PF={最高车速,最大爬坡度,加速时间,百公里耗电量,续驶里程,动力系统成本}.

用关联矩阵来表示车辆性能和技术特性的耦合关系,为了确保数据的可靠性,选取几款同类型电动汽车作为竞争产品进行分析.技术竞争性评价矩阵由竞争产品的技术特性数值组成,将其作为比较数列;市场竞争性评价矩阵由顾客对性能需求的满意度组成,将其作为参考数列,以此构成灰色系统,关联度的大小反映顾客需求与技术特性之间的耦合程度.

设有m个顾客需求,a个技术特性,s个竞争产品,市场竞争性评价矩阵M=[d1,d2,…,dm],技术竞争性评价矩阵T=[x1,x2,…,xa],技术特性对第j个顾客需求的关联关系为rj,则令x0=dj(j=0,1,…,m)为参考数列;x1,x2,…,xa为比较序列,构建灰色系统.

对原数据进行无量纲化,极大型指标的处理方法是

(1)

极小型指标的处理方法是

(2)

(3)

式中:b=0,1,…,a;e=1,2,…,s;ρ为分辨系数,ρ∈[0,1],一般取ρ=0.5.

关联度的计算公式为

(4)

式中:j=1,2,…,m;rj(b)为第j个顾客需求与第b项技术特性的相关度,构成需求-特性关联矩阵r.

1.2基于粗糙数的顾客需求重要度

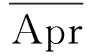
(5)

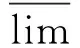
(6)

式中,NL和NU分别是Rl下近似和上近似所包含类的个数.

RNM(Rl)为粗糙数RN(Rl)上、下极限的中间值,其表达式为

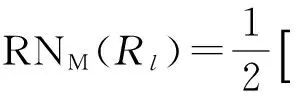
(7)

(8)

则第j个顾客需求的重要度wCR j为

(9)

1.3技术特性重要度

技术特性的重要度代表设计指标对顾客满意度的贡献度,第b项技术特性的重要度wPFb为

(10)

2电动汽车动力系统参数设计与优化

根据对车辆动力性和经济性指标的设计要求,计算电机的最高转速、峰值功率、额定功率、峰值转矩和电池单体的数目等特性参数,然后基于正交实验法,以这些需求值在其可取范围内进行优化设计,分析因素的灵敏度和性能最优的因素水平组合.

2.1驱动电机参数匹配

电机的特性参数决定车辆的动力性能,电机的最高转速nmax由最高车速vmax决定:

nmax≥vmaxi0/(0.377R)

(11)

式中,i0为主减速器传动比,R为轮胎半径.当电动汽车省去变速器,利用主减速器直接档驱动时,可以大大降低整备质量,提高能源利用率.当利用主减速器直接档驱动时,电机从基速nb=nmax/β(β为基速比)向上调速的范围需要足够大,但也不宜太大,β≥2.5[12].

额定功率需满足最高车速行驶功率需求:

(12)

式中,m为汽车质量,g为重力加速度,f为滚动阻力系数,CD为空气阻力系数,A为迎风面积,ηt为传动系效率.

峰值转矩Tmax要满足最大爬坡时的转矩需求:

(13)

式中,αmax为最大爬坡度,vp为爬坡速度.

峰值功率Pmax满足汽车的加速性能,汽车从静止到加速末速度vf的加速时间要求不大于t,则

(14)

根据电机特性可确定其转矩T为

(15)

2.2动力电池参数匹配

电池作为主能源,要保证汽车的动力性能和续驶里程的要求.根据功率需求,电池单体数要满足：

(16)

式中:κ是最大放电倍率;Cb是单体电池电容;Ub是单体电池电压;ηmc是电机及其控制器效率,电机效率决定了能量从驱动电机转移到传动系统过程中的能量损耗[13],通过电机峰值功率、峰值转矩、最高转速、额定转矩及电池组额定电压等参数可以预估永磁同步电机效率[14].

根据续驶里程的能量需求,电池单体数要满足

(17)

式中:QNEDC是车辆在NEDC工况下的百公里耗电量,单位是kWh;SNEDC是车辆在NEDC工况下的续驶里程,单位是km.则所需要的电池单体数N=max{NP,NS}.

2.3参数灵敏度分析

正交试验中考察的结果称为指标,对试验指标可能有影响的参数称为因素,每个因素在试验中进行比较的试验条件称为水平,根据因素个数和水平数选择正交表.

对优化方案进行仿真分析得到各指标的实验结果,设为因素z在y水平下多次试验结果的平均值,由Kyz的大小可以判断因素z的最优水平,各因素的最优水平组合即为最优水平组合.

设RAz为第z个因素的极差,

(18)

RAz反映了因素z水平变动时试验指标的变动幅度,RAz越大,说明该因素对试验指标的影响越大,因此该因素越重要,依据极差RAz的大小就可以判断因素的主次顺序[15],即指标对各因素的灵敏度.

3实例分析

基于Matlab平台建立纯电动汽车优化设计模型,以本研究中心的一款纯电动样车为例,根据确定电动汽车技术特性加权因子、动力系统参数匹配和优化设计的方法及步骤对其进行改进.

3.1确定技术特性重要度及设计值

收集了市场上4款同类型的电动汽车作为竞争产品,与该产品构成的技术竞争性评价矩阵为

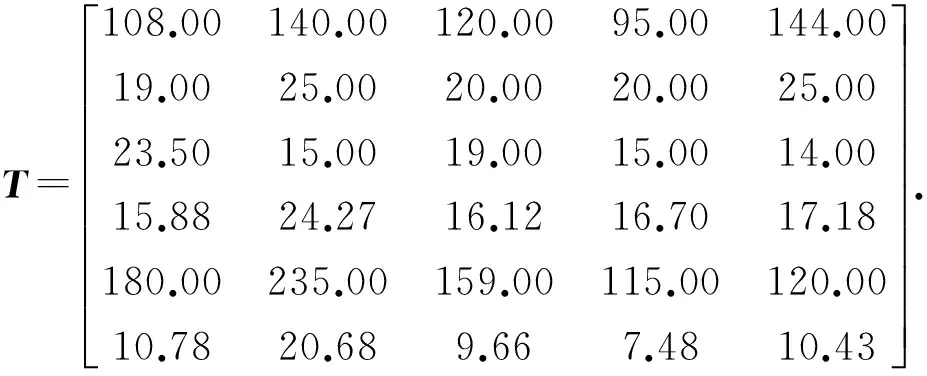
对5款产品的顾客需求满意进行调查,得到市场竞争性评价矩阵为

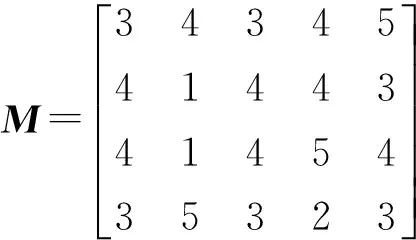
分别对T和M进行无量纲化,然后根据式(3)和(4)得到需求-特性关联矩阵：

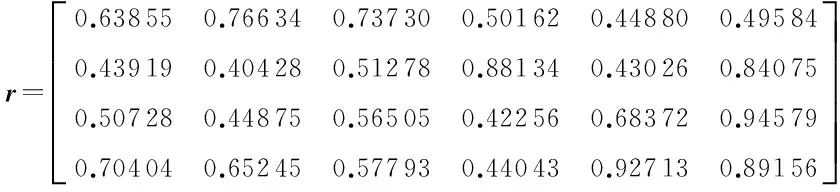
由专家团对顾客需求的车辆性能重要度进行打分,评价等级分为5级(低、较低、中、较高、高),分数分别是1、3、5、7和9,结果如表1所示.

表1顾客需求重要度调查结果

Table 1Survey results of importance ratings of customer demands

wCR=(0.224 07,0.194 59,0.331 60,0.249 70).

由此可知顾客需求重要度由大到小是:购买价格低,续驶里程长,动力性能好,使用费用低.对于纯电动汽车，顾客首要需求的性能是购买价格低,其次是续驶里程满足使用要求,纯电动汽车的使用费用普遍较低,体现其节能优势.

由式(10)计算得到电动汽车技术特性重要度wPF=(0.153 59,0.150 79,0.160 06,0.143 25,0.174 77,0.217 54).

由此可知技术特性重要度由大到小的顺序是:动力系统成本,续驶里程,加速时间,最高车速,最大爬坡度,百公里耗电量.权重最大的是动力系统成本,这与当前面临的电动汽车成本普遍高于传统汽车的问题相一致;其次是续驶里程,提高续驶里程必然增加系统成本.

动力性和经济性设计目标值设定如下:最高车速vmax≥120 km/h,15 km/h时的最大爬坡度αmax≥25%，0～100 km/h的加速时间t≤16 s,续驶里程SNEDC≥200 km.

3.2动力系统参数匹配

该款纯电动汽车的整车参数为:m=1 100 kg,f=0.15,CD=0.3,A=1.5 m2,R=0.309 5,ηt=0.96,i0=4.54.车载电池单体参数为:Cb=100 Ah,Ub=3.3 V,DOD=0.9,ηmc=0.9,k=3.

首先根据式(17)确定满足能量需求的电池单体数NS≥97,电池增加使整备质量增加,电池质量mb=NCbUb/Q,Q=120 Wh/kg[16],电池系统成本Cbat=NbCbUbC*,C*=3 元/Wh.

将整车参数代入式(11)-(13),求得:nmax≥4 670 r/min,Pe≥19.3 kW,Tmax≥296 Nm.

根据式(14)和(15)求得0～100 km/h加速时间和最大爬坡需求转矩的等值线,见图1.

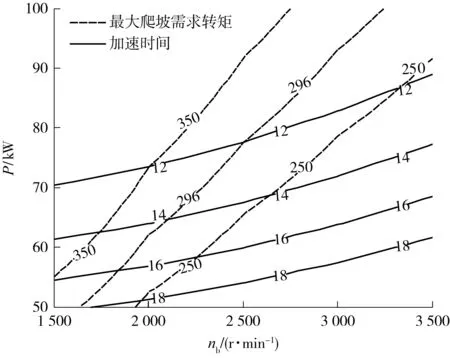
图1　加速和爬坡性能曲线Fig.1　Acceleration and climbing performance curves

由式(6)计算得到满足功率需求的电池单体个数N≥75,因此最终的N≥97.

由于电池和电机参数对其成本影响较大,故动力系统成本为电池系统和电机系统的成本之和:Cbm=Cbat+Cmot.

3.3基于正交试验的优化方案设计

表2动力系统参数设计因素水平表

Table 2Level table of powertrain parameter design factors

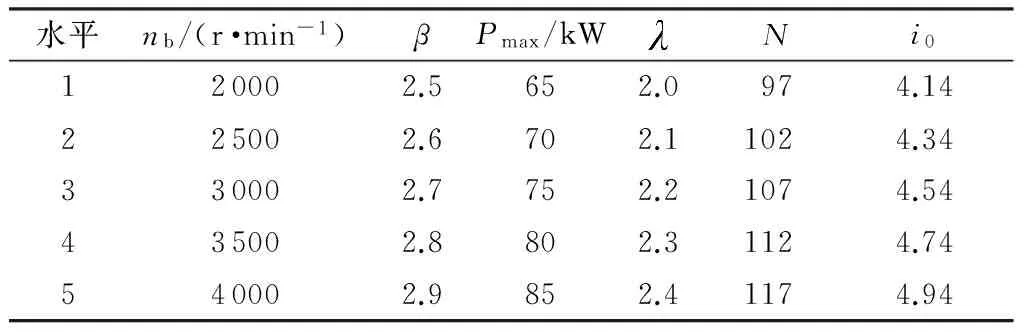
水平nb/(r·min-1)βPmax/kWNi0120002.5652.0974.14225002.6702.11024.34330002.7752.21074.54435002.8802.31124.74540002.9852.41174.94

根据表2的因素水平表,选择L25(56)正交表进行方案设计,共有25个试验方案,进行25次性能仿真,得到电动汽车的最高车速(vmax)、最大爬坡度(αmax)、0～100 km/h的加速时间(t)、NEDC工况下的百公里耗电量(QNEDC)、续驶里程(SNEDC)和动力系统成本(Cbm),结果见表3.

表3性能仿真结果

Table 3Performance simulation results

序号vmax/(km·h-1)αmax/%t/sQNEDC/kWhSNEDC/kmCbm/万元1140.9226.46614.68618.075177.1012.3082139.8030.08913.37918.222184.7312.9783138.7833.99112.24118.421191.6813.6484137.8538.20711.40718.538199.3814.3185136.9942.78310.61118.734206.1014.9886147.6226.48414.30318.651198.1613.9687156.2923.21214.95418.850204.8314.6388158.4127.43812.93318.213175.7612.8339174.3830.65111.90318.879178.3013.50310153.3423.47615.65018.449191.3913.29811154.1222.69014.95718.431182.6213.15312170.0825.31313.62719.165184.2413.82313170.7121.98314.84119.332191.1914.49314150.0616.97819.41918.760205.8214.28815152.6520.20916.49418.219175.7012.48316166.4618.96616.98319.418198.8314.81317168.0822.18814.66619.135167.2913.00818147.8717.01919.20518.452182.4212.80319149.6315.00921.29618.677189.0513.47320165.5816.93718.95219.489189.6414.14321164.7816.94720.40619.942177.0613.99822144.8913.03525.31119.107193.4313.79323160.8614.74021.72920.025192.8114.46324162.8817.38018.40819.502164.1412.65825163.8915.16224.02119.735170.5613.328

3.4技术特性参数灵敏度分析

计算性能指标在各因素各水平的试验平均值,并绘制因素水平变化趋势,如图2所示.从图中可以清晰地看出各因素水平变动时各指标的变动幅度,根据实验平均值可以得到各评价指标最优时的动力系统配置参数,即各指标的最优水平组合.

电机基速和峰值功率对各性能指标的影响趋势曲线的斜率都比较大,故其取值与各性能指标的大小关系较大;电机的基速比、过载系数和传动系的传动比对各性能指标的影响趋势曲线基本上都是一条水平线,即其取值对各性能指标的影响较小;单体电池个数对NEDC工况下的百公里耗电量和系统成本指标的影响最大.

为准确描述设计因素对评价指标的影响程度,采用极差分析法分析各指标对因素的灵敏度,因素的极差越大说明其变化对指标产生的影响越大,因此可以使用因素极差值来表示指标对因素的灵敏度.各指标对因素的灵敏度如图3所示.

当需要改善电动汽车某个性能时,可依据极差来调整其灵敏度大的参数,使该性能达到设定要求.

图2　电动汽车性能指标的试验结果 Fig.2　Experimental results of performance indexes of electric vehicle

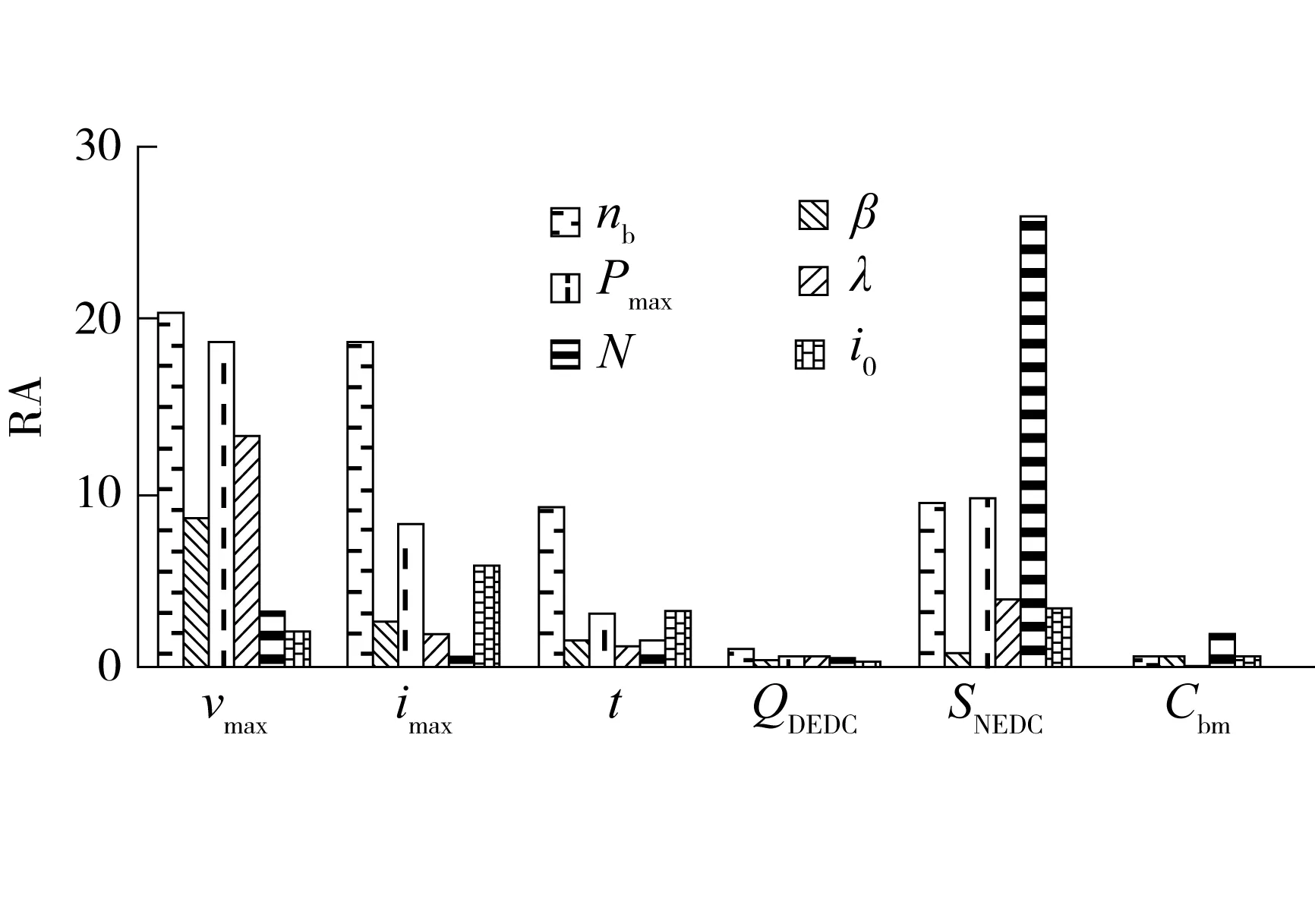
图3　各指标的极差值 Fig.3　Range value of every index

3.5动力系统参数的多目标优化

由3.4节的分析可知,当一个性能得到提升时,另一个性能可能会降低,为了使所有的性能都能满足要求,需要进行多目标优化设计.灰色关联分析法是根据因素之间发展趋势的相似或相异度来衡量因素间关联度的方法,可以解决这种多目标优化设计问题.

将所有方案作为比较序列,每个指标的最优值组成参考序列,构成灰色系统,首先将指标值无纲量化,然后根据式(3)计算第p个方案的第j个指标值与最优值的关联系数εp(j),定义第p个方案的整车综合性能指标系数为

(19)

式中,wPF(j)为第j个技术特性指标的权重因子.Dp越大,说明第p个方案的整车综合性能越好,从而将多目标优化转换成对整车综合性能指标系数的单目标优化问题.

优化数学模型为

(20)

根据综合性能指标系数的大小对方案进行优劣排序,各试验方案的综合性能指标系数计算结果如图4所示.

图4　各试验方案下车辆综合性能指标系数Fig.4　Coefficients of vehicle comprehensive performance indexes in each test scheme

求得综合性能指标系数在各因素各水平的实验平均值,并绘制因素水平变化趋势,如图5所示.

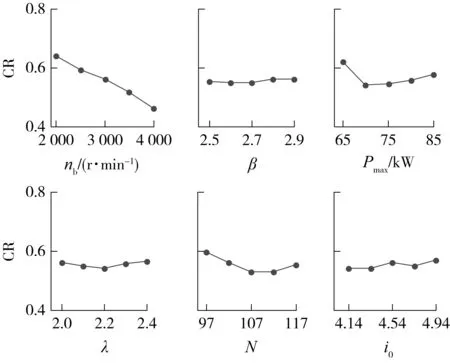
图5　纯电动汽车整车综合性能指标实验结果Fig.5　Experimental results of comprehensive performance indexes of electric vehicle

从图5可以看出各因素水平变动时整车综合性能指标的变动幅度及其最优水平组合,采用极差分析法分析其对因素的灵敏度,结果如表4所示.

表4综合性能指标系数最优水平组合和极差

Table4Optimallevelcombinationandrangeofcomprehensiveperformancecoefficients

因素nbβPmaxNi0k10.638290.552140.618080.558900.595180.54134k20.592220.547520.540040.549390.558870.54105k30.562010.549800.544770.538970.530610.56180k40.515270.562280.557970.557020.530370.54981k50.459730.559870.574920.563230.552500.56966RA0.178560.014760.078040.024260.064810.02861

可以看出,综合性能的最佳水平组合是

3.6动力系统参数优化设计结果分析

将优化得到的汽车综合性能最优的水平组合的动力系统参数分别代入性能仿真模型,求解出各性能指标值,并与原车性能进行对比分析,结果如表5所示.由表中可知,与优化前相比,优化后车辆的动力系统成本增加了14.2%,但整车动力性能的各项指标都得到了很大的提升,续驶里程也提升了11.3%,其整车综合性能比优化前有较大的提高.

表5优化前后车辆的性能对比

Table 5Performance comparison before and after optimization

指标vmax/(km·h-1)αmax/%t/sQNEDC/kWhSNEDC/kmCbm/万元D优化前10819.023.515.8818010.780.574优化后13228.713.015.9820012.310.759变化率/%22.551.1-44.80.611.314.232.3

4结论

文中以电动汽车市场需求性能为驱动,构建了电动汽车动力系统参数设计与综合优化方法.基于QFD建立了车辆市场需求性能与技术特性的耦合模型,应用灰色关联法和粗糙数来确定电动汽车开发过程中所需的综合性能的权值与技术重要度的分配;以综合性能最优为目标,采用基于正交试验的优化设计方法分析各设计参数对不同性能的灵敏度；为改善车辆性能提供直接依据,利用灰色关联法获得综合性能最优解.车辆动力系统的设计优化结果表明,优化后车辆的综合性能指标得到显著的提升,验证了文中方法的正确性,为电动汽车动力系统参数设计与优化提供了一种有效的方法.

参考文献：

[1]朱曰莹,赵桂范,杨娜,等.电动汽车动力系统参数匹配及优化 [J].哈尔滨工业大学学报,2013,45(7):90-95.

ZHU Yue-ying,ZHAO Gui-fan,YANG Na,et al.Parameters match and optimization for the dirve system of electric vehicle [J].Journal of Harbin Institute of Technology,2013,45(7):90-95.

[2]ZHAO Danwei,WANG Ruijun.Research on parameters matching of electric sanitation vehicle powertrain [C]∥Proceedings of 2013 International Conference on Mecha-nical and Automation Engineering.Jiujang:IEEE,2013:95-97.

[3]周胜,周云山.纯电动汽车动力匹配及计算仿真 [J].计算机真,2013,30(2):135-139.

ZHOU Sheng,ZHOU Yun-shan.Power matching and calculation simulation of pure electric vehicle [J].Computer Simulation,2013,30(2):135-139.

[4]尹安东,杨峰,江昊,等.基于iSIGHT的纯电动汽车动力系统匹配优化 [J].合肥工业大学学报(自然科学版),2013, 36(1):1- 4.

YIN An-dong,YANG Feng,JIANG Hao,et al.Matching and optimization of pure electric vehicle drivetrain with iSIGHT [J].Journal of Hefei University of Technology(Natural Science),2013,36(1):1- 4.

[5]黄康,罗时帅,王富雷.纯电动汽车动力系统传动比优化设计 [J].中国机械工程,2011,22(5):625- 629.

HUANG Kang,LUO Shi-shuai,WANG Fu-lei.Optimization design of electric vehicle transmission gear ratio [J].China Mechanical Engineering,2011,22(5):625-629.

[6]胡明辉,谢红军,秦大同,等.电动汽车电机与传动系统参数匹配方法的研究 [J].汽车工程,2013,35(12):1068-1073.

HU Ming-hui,XIE Hong-jun,QING Da-tong,et al.A study on the parameter matching between the motor and transmission system of an electric vehicle [J].Automotive Engineering,2013,35(12):1068-1073.

[7] 房立存,秦世引.基于多目标遗传算法的混合电动汽车参数优化 [J].汽车工程,2007,29(12):1036-1040.

FANG Li-cun,QIN Shi-yin.Parameters optimization of hybrid electric vehicle based on multi-objective genetic algorithms [J].Automotive Engineering,2007,29(12):1036-1040.

[8]周兵,江清华,杨易,等.两挡变速器纯电动汽车动力性经济性双目标的传动比优化 [J].汽车工程,2011,33(9):792-797,828.

ZHOU Bing,JIANG Qing-hua,YANG Yi,et al.Transmission ratio optimization with dual objectives of power performance and economy for a two-speed electric vehicle [J].Automotive Engineering,2011,33(9):792-797,828.[9]朱曰莹,王子龙,韩光省,等.基于循环工况的电动汽车传动系参数正交优化设计 [J].中南大学学报(自然科学版),2013,44(增刊2):216-221.

ZHU Yue-ying,WANG Zi-long,HAN Guang-sheng,et al.Orthogonal optimal design for drive system parameter of electric vehicle based on vehicle driving cycle [J].Journal of Central South University(Science and Technology),2013,44(Suppl 2):216-221.

[10]MICHALSKI A,DZIADAK B.Quality engineering tools used to design & optimize a mobile measurement station [J].IEEE Instrumentation & Measurement Magazine,2010,13(1):33-38.

[11]ZHAI Lian-Yin,KHOO Li-Pheng,ZHONG Zhao-Wei.A rough set enhanced fuzzy approach to quality function deployment [J].International Journal of Advanced Manu-facturing Technology,2008,37(5):613- 624.

[12]姬芬竹,高峰.电动汽车驱动电机和传动系统的参数匹配 [J].华南理工大学学报(自然科学版),2006,34(4):33-37.

JI Fen-zhu,GAO Feng.Matching of motor and powertrain parameters of electric vehicle [J].Journal of South China University of Technology(Natural Science Edition),2006,34(4):33-37.

[13]YU Jingnuo,LIANG Guihang,Wang Jian,et al.Pure electric vehicle driving system parameter matching in motor higher efficiency interval [C]∥Proceedings of 2012 International Conference on Systems and Informa-tics.Yantai:IEEE,2012:594-597.

[14]SOYLU Seref.Electric vehicles-modeling and simulations [M].Rijeka:InTech,2011:15-17.

[15]李炎隆,李守义,丁占峰,等.基于正交试验法的邓肯-张E-B模型参数敏感性分析研究 [J].水利学报,2013,44(7):873- 879.

LI Yan-long,LI Shou-yi,DING Zhan-feng,et al.Thesensitivity analysis of Duncan-Chang E-B model parameters based on the orthogonal test method [J].Journal of Hydraulic Engineering,2013,44(7):873- 879.

[16]周飞鲲.纯电动汽车动力系统参数匹配及整车控制策略研究 [D].长春:吉林大学,2013.

责任编辑：许花桃

Parameter Optimization of Powertrain System for Electric Vehicles Oriented to Performance Requirements

XIONGHui-yuan1,2WUXiao-li1ZONGZhi-jian1,2YULi-min1

(1. School of Engineering, Sun Yat-Sen University, Guangzhou 510006, Guangdong, China;2. Institute of Dongguan-Sun Yat-Sen University, Dongguan 523808, Guangdong, China)

Abstract:Proposed in this paper is an integrated design and optimization method of powertrain parameters for electric vehicles on the basis of QFD (Quality Function Deployment) and orthogonal test, which promotes the comprehensive performance of electric vehicles effectively. Firstly, a QFD-based coupling model considering both customer requirements and technical characteristics is set up, and the weighting factors of technical characteristics are determined by applying rough number and grey correlation method. Secondly, an optimization model of powertrain parameters is constructed through orthogonal test, with vehicle comprehensive performance being taken as the objective. Then, the comprehensive performance coefficients of vehicles are obtained by means of grey correlation method, and the optimal solution to multi-objective optimization as well as the sensibility analysis of performance factors is dealt with. Finally, a design and optimization model on Matlab platform is established and is further verified with an electric vehicle. An increment of 32.3% in comprehensive performance is obtained, which verifies the effectiveness of the proposed method.

Key words:electric vehicle; quality function deployment; orthogonal test; sensibility analysis; grey correlation method

收稿日期：2015-02-12

*基金项目：广东省战略性新兴产业核心技术攻关项目(2012A010702001);东莞市重大科技专项(2011215155)

Foundation item:Supported by the Key Technology Research Project of Strategic Emerging Industry in Guangdong Province(2012A010702001)

作者简介：熊会元(1973-),男,博士,副教授,主要从事电动汽车集成设计优化技术研究.E-mail:xionghy@mail.sysu.edu.cn

中图分类号：U462.1

doi：10.3969/j.issn.1000-565X.2016.03.010