基于风险的桥梁多灾害下合理冲刷深度研究*

杨延凯　马如进　陈艾荣

(同济大学 桥梁工程系， 上海 200092)

基于风险的桥梁多灾害下合理冲刷深度研究*

杨延凯马如进陈艾荣

(同济大学 桥梁工程系， 上海 200092)

摘要：为了在桥梁设计和评估中充分考虑多灾害影响，基于一致风险原则，提出桥梁在考虑冲刷和地震联合灾害作用条件下的分析框架,开展了考虑地震灾害的合理冲刷深度研究.首先对桥梁进行考虑冲刷的地震易损性分析，获得结构的易损性曲线和易损面；根据两种灾害的危险性模型，获得不同给定冲刷深度下失效概率与冲刷深度的关系及联合失效概率.然后将联合失效概率所对应的冲刷深度作为两种灾害组合时的合理冲刷深度，进一步与设计冲刷深度比较，得到地震和冲刷多灾害下桥梁设计中所需要的冲刷荷载组合系数，并以一悬索桥为例说明分析过程.文中方法有效考虑了桥梁整体风险和经济性,可为地震和冲刷联合灾害作用下不同类型和大小的桥梁的探索分析提供基础.

关键词：桥梁；风险；地震；冲刷；多灾害

桥梁在公路网中占有重要的地位，同时也最容易受到地震、飓风、冲刷以及船撞等灾害的威胁，一旦遭到破坏，不但其自身要面临损失，整个交通网络的使用功能也会受到影响，因此，充分考虑灾害对桥梁的影响，是明确区域性交通畅通的重要条件.当前的桥梁设计规范[1]中，各种灾害被抽象成单独的荷载，并以不同的设计水平作用于桥梁(如千年一遇的地震强度和百年一遇的河床冲刷深度)，无法对其直接组合.虽然基于可靠度的设计方法在桥梁车辆荷载和恒载方面已经得到了应用，并完成了对荷载组合系数的校验[1]，但在其他荷载的组合问题上，一般是基于工程经验，从理论上并没有得到严格的论证[2].各种极端灾害发生概率很低，但会对桥梁产生明显的损伤，造成人员伤亡和经济损失.世界范围内，地震和冲刷是两个最常见的导致桥梁损伤的极端灾害[3]，建立基于风险的考虑地震和冲刷灾害组合的研究框架，明确两种灾害的组合方式是十分必要的.

在房屋建筑领域，已经有研究者基于极限状态方法[4]和风险思想[5- 6]对多灾害问题进行了研究，并评估荷载组合系数.对于桥梁结构，虽然很多研究人员已经对其地震灾害下的性能进行了探讨[7-10]，但基于风险思想的考虑多灾害组合的研究很少，特别是针对地震和冲刷灾害组合的研究.Ghosn等[2]基于Ferry-Borges 模型和Monte Carlo方法对公路桥梁面对的多种极端灾害(如地震、大风、冲刷和船撞等)进行了综合研究并得到了组合系数，但研究只是针对桥墩桥台的倾覆极限状态，无法全面反映桥梁的破坏过程，Sun等[11]基于Ferry-Borges模型，提出了考虑地震和重车荷载的概率模型.Swagata等[12]通过易损面方法研究了公路桥梁在地震和冲刷灾害下的组合效应.You等[13]分析了冲刷对桥梁地震易损性的影响，并分析了桥梁在确定的冲刷深度下的地震经济损失.这些研究没有讨论如何考虑地震荷载和冲刷的组合这一核心问题.Alipour等[14]研究了钢筋混凝土桥梁在地震和冲刷两种灾害下的冲刷效应组合系数，但忽略了单独地震灾害下的失效问题，可能会低估桥梁的失效概率.为了避免在灾害组合分析中对边缘效应的忽略，应采用基于风险的方法研究地震和冲刷组合对桥梁的影响.

文中提出一种用概率方法来考虑地震和冲刷两种灾害联合作用的组合方法，处理两种灾害下的结构需求，并以此获取合理的冲刷深度和荷载组合系数.首先，根据提出的桥梁在两种灾害下的需求模型，计算桥梁在不同冲刷深度下的地震易损性曲线以及在地震和冲刷两种灾害下的易损面；然后通过危险性分析得到两种灾害的概率模型，获得不同冲刷深度下的失效概率与冲刷深度的关系及联合失效概率；联合失效概率所对应的冲刷深度为两种灾害组合时的合理冲刷深度，进一步与设计冲刷深度比较，得到联合灾害下的设计冲刷荷载系数.并以一位于冲刷效应明显且地震设防较高处的大跨径自锚式悬索桥为例对以上方法进行说明.

1多灾害下易损性分析方法

1.1多灾害下的地震需求模型

结构的易损性是指结构发生某个损伤状态的条件概率，通过结构的概率需求模型与能力概率模型比较得到结构的易损性.在结构抗震领域，经过概率地震需求模型(PSDM)的发展和应用，已经可以获得桥梁在地震灾害下的概率响应.对于大跨度桥梁，一般采用需求能力比模型进行分析[15]，也就是应用结构需求能力比值与荷载强度的关系获得结构的概率“需求”模型.采用文献[15]的分析方法，如式(1)所示：

μ=a(lnPGA)2+blnPGA+c

(1)

式中：a、b和c为回归参数；PGA为地震加速度峰值；μ=Sd/Sc，为对数坐标系下回归得到的需求能力比均值，Sd和Sc分别表示需求和能力.标准差

(2)

式中，O为回归分析的残差平方和，n为回归样本个数.

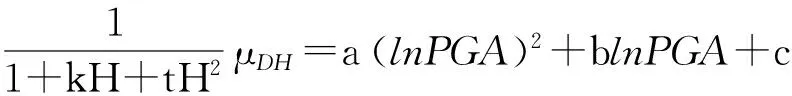
(3)

采用文献[16]中50条地震波(分别进行系数缩放，得到不同的PGA水平)对不同冲刷深度的非线性时程分析，获得桥梁各构件地震响应峰值，并在对数坐标系下回归分析，获得结构概率需求模型.

1.2易损性曲线和易损性曲面

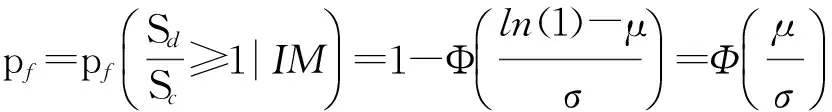
(4)

式中， Φ(·)为标准正态分布函数.影响结构失效概率的主要因素是能力和需求的分布类型和分布参数，由于文中重点关注地震下结构的易损性，结构能力不确定性影响相对于地震荷载的不确定性影响较小[17]，故不考虑结构能力的不确定性.

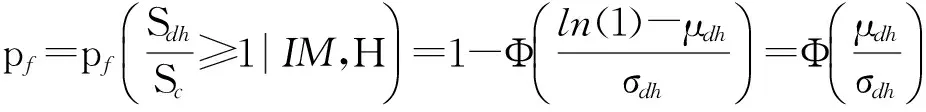
(5)其中，Sdh为考虑地震和冲刷的联合需求，μdh和σdh分别为考虑两种灾害联合的对数平均值和标准差.

1.3结构的性能状态

明确结构的失效或者损伤状态，需要定义结构单元的能力.根据桥梁结构构件的重要性程度、对桥梁使用功能的影响以及维修费用，不同的构件采用不同的方式定义损伤状态.例如桥墩桥塔或者基础破坏会直接影响桥梁竖向和横向的承载能力，严重破坏直接导致桥梁得倒塌，而桥梁支座的破坏会影响桥梁的使用，可对其进行维修和更换.文中只考虑桥梁最重要桥塔结构的损伤状态，不考虑支座的失效及损伤，假定支座具有足够的活动空间适应地震引起的位移.

对于钢筋混凝土柱，有不同的指标来评估结构的损伤状态，如层间位移比、位移延性和曲率延性等[14].冲刷会明显改变桥塔结构的刚度，使结构在同样的荷载条件下产生更大的位移，采用层间位移和位移延性指标很可能会过大地估计当前结构的损伤状态，而截面曲率直接反映截面内不同位置钢筋和混凝土的应力应变情况[18].所以文中采用混凝土材料和钢筋材料不同的应变情况所对应的峰值截面曲率来定义结构的损伤状态，如表1所示[15].

表1截面损伤等级及对应参数1)

Table 1Section damage level and the corresponding parameters

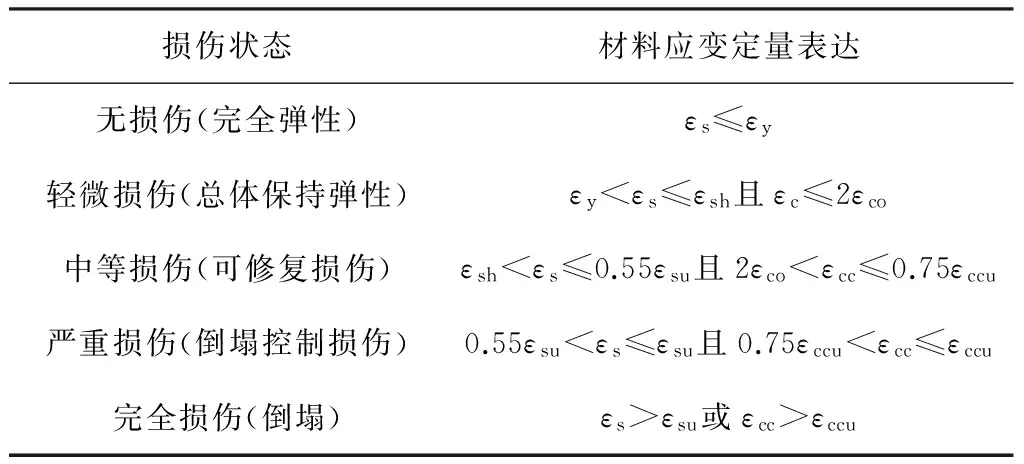
损伤状态材料应变定量表达无损伤(完全弹性)εs≤εy轻微损伤(总体保持弹性)εy<εs≤εsh且εc≤2εco中等损伤(可修复损伤)εsh<εs≤0.55εsu且2εco<εcc≤0.75εccu严重损伤(倒塌控制损伤)0.55εsu<εs≤εsu且0.75εccu<εcc≤εccu完全损伤(倒塌)εs>εsu或εcc>εccu

1)各符号参见文献[15]，其中εsh=0.015，εsu=0.09，εco=0.002.

2地震和冲刷灾害危险性分析

2.1地震灾害危险性分析

地震灾害危险性一般以给定场地发生大于指定强度IM的概率来表达，地震强度一般以地震动峰值加速度PGA或者指定周期的谱加速度SA表示.根据中国地震烈度调查及研究成果，地震危险性用极值III型分布来拟合地震烈度的概率分布，分布函数[16]表达为

(6)

(7)

取烈度与PGA的关系[16]如式(8)所示：

PGA=10(im lg 2-0.01)

(8)

式中， PGA单位为gal(cm/s2).

这样就获得了地震危险性及其概率密度方程，考虑PGA为地震强度指标的地震危险性曲线在对数坐标系中如图1所示.

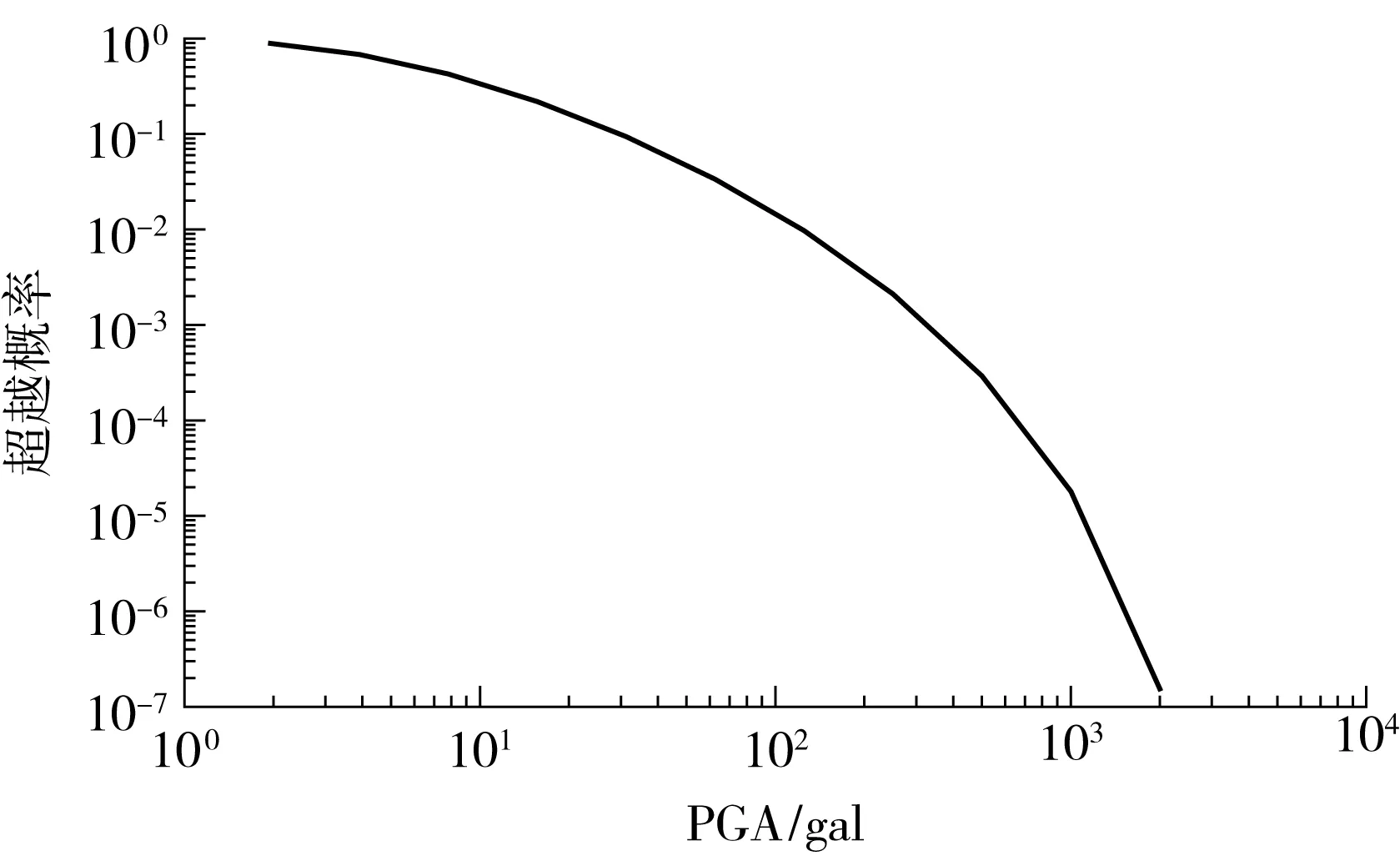
图1　地震危险性曲线Fig.1　Earthquake hazard curve

2.2冲刷灾害危险性分析

冲刷是指桥梁基础周围土层被流水侵蚀，主要包括3种形式[14]：①自然冲刷；②一般冲刷；③局部冲刷.一般认为局部冲刷是最明显的冲刷形式[14]，文中主要考察桥位的局部冲刷问题，同样这种方法可以扩展到其他形式的冲刷.

与地震荷载不同，冲刷本身不能作为一种荷载[1]，而是通过改变桥梁自身状态对其他灾害下的结构响应进行影响.对于桥梁的冲刷问题，静力计算一般按照依据最不利原则以最大冲刷深度进行考虑，而对于动力计算时没有具体的规定.参考美国联邦公路局的HEC NO.18[19]中关于桥梁冲刷深度的计算公式，同时考虑Johnson 等[20]的修正，计算公式为

(9)

(10)

式中: v为水流速度，可通过河流断面的尺寸和流量计算得到；g为重力加速度.

为了获得冲刷深度的概率分布，需要明确公式中各参数概率模型.当前对于上式中很多参数没有具体的概率分析，根据已有的研究成果，部分参数分布如表2所示，其余参数按规定取确定值.年最大流量的分布一般按照对数正态分布考虑，文中平均值和标准差分别取3 520m3/s和460m3/s.

表2冲刷深度参数概率分布

Table 2Variables for the probabilistic scour depth

变量均值变异系数分布类型s0.570.6正态分布[20]K210.05正态分布[12]K31.10.05正态分布[21]

根据式(9)中参数的分布情况，通过Monte-Carlo数值模拟得到冲刷深度的数值样本.利用Matlab共进行10 000次的数值模拟，根据中心极限定理，按照K-S方法拟合(5%显著性水平)的冲刷深度概率模型符合对数正态分布，冲刷深度危险性曲线如图2所示，概率密度函数可表达为

(11)

式中，η和ξ分别为冲刷深度的对数平均值和标准差，根据模拟结果，分别为1.65m和0.18m.

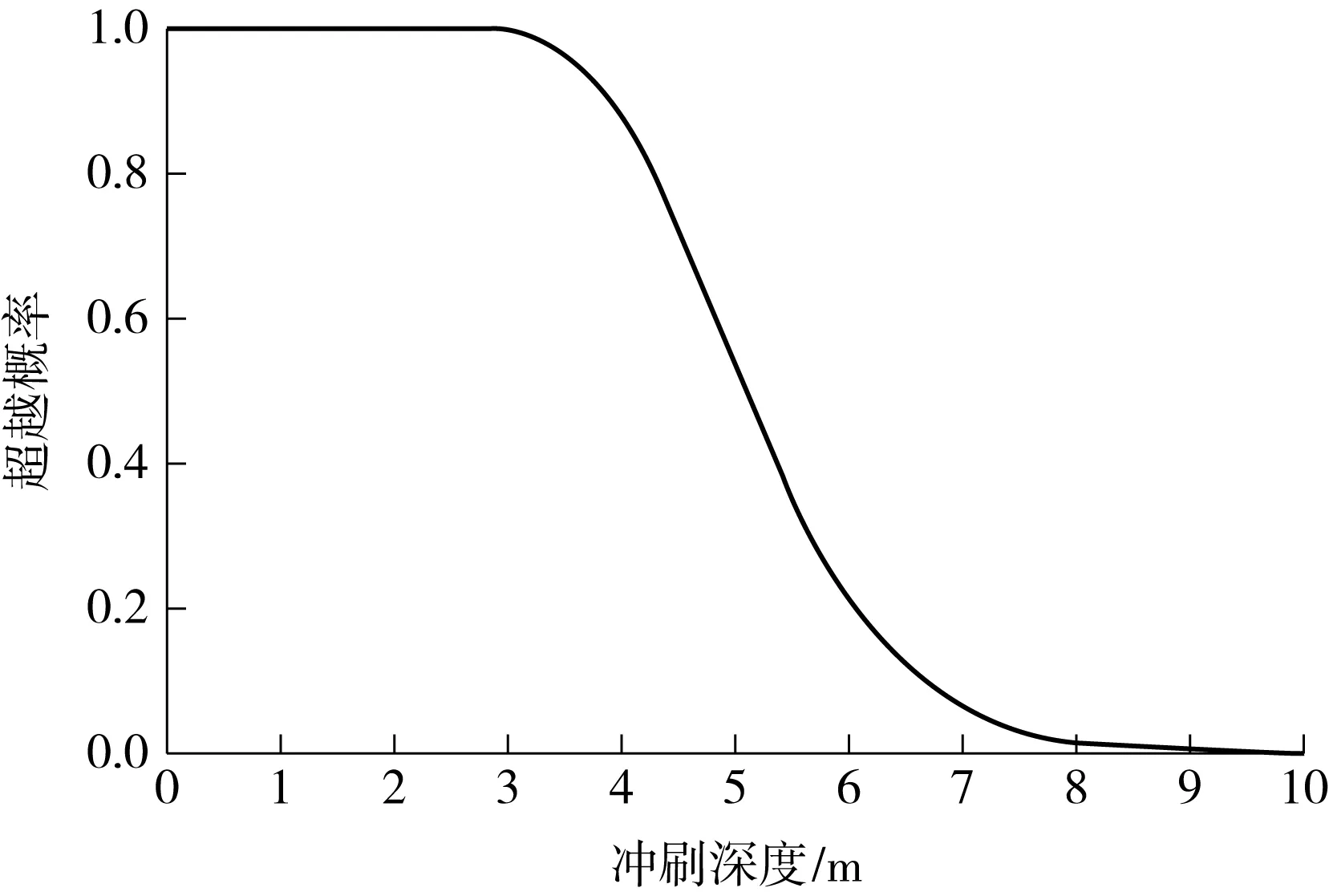
图2　冲刷危险性曲线Fig.2　Scour hazard curve

3考虑联合效应的合理冲刷深度确定方法

对于工程结构而言，单一灾害下或多灾害下的失效概率是判断结构是否可靠的依据.对于冲刷灾害和地震灾害两种灾害而言，冲刷本身并不是以荷载的方式作用在结构上，而是通过地震荷载效应体现其对结构的影响，所以在结构设计时如何选择合理的冲刷深度与地震组合十分重要.

3.1两种失效概率

考虑地震和冲刷灾害下的桥梁失效概率分为两种，一种是给定冲刷深度下桥梁在地震灾害下的失效概率，一种为综合考虑两种灾害的危险性的联合失效概率.

给定冲刷深度下，桥梁在地震灾害下的平均年失效概率可表达为式(6)的卷积形式：

(12)

式中：Fsh(im)为方程(4)定义的给定冲刷深度的易损性函数；fIM(im)为地震灾害的概率密度函数，代表超过不同IM水平的地震的年平均可能性.

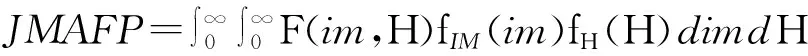
(13)

式中，F(im,H)为方程(5)定义的以地震强度im和冲刷深度H为自变量的易损面函数.

3.2合理冲刷深度的确定

为综合考虑桥梁在两种灾害下的性能状态，避免忽略单独灾害下结构失效的边缘效应，以考虑灾害危险性和结构易损性的失效概率JMAFP为当前桥梁结构的风险标准.通过方程(14)得到与JMAFP相等的MAFP_h，对应的冲刷深度Hr为考虑联合灾害分析时的合理冲刷深度.进一步为了桥梁设计需要，可根据方程(15)，得到两种灾害分析时的冲刷荷载系数.

MAFP_h(Hx)=JMAFP

(14)

式中，Hx为确定的合理冲刷深度.

进一步，根据设计冲刷深度，得到冲刷荷载系数γs：

(15)

式中，Hd为根据式(9)中确定的参数计算的设计冲刷深度.

4研究实例

4.1研究实例介绍

文中以一特大跨径自锚式悬索桥为研究对象，桥梁主跨跨径为406 m，桥塔采用门式桥塔，塔高为140 m，基础为群桩基础，基础最大冲刷深度为22.57 m，由于南塔位于河漫滩上，北塔处于主河道，所以文中主要考虑北塔的冲刷问题，全桥布置及塔桩的配筋情况如图3所示.

图3　桥梁立面图及桥塔和桩柱配筋图(单位：cm)Fig.3　Layout of the bridge and reinforcement of tower and piles(Unit:cm)

采用有限元模拟软件Opensees[22]模拟结构考虑冲刷和地震荷载下结构的响应.上部结构主梁、主缆采用弹性梁柱单元模拟，桥塔和桩柱采用考虑材料强度的非线性单元模拟，采用纤维截面考虑钢筋和混凝土的应变情况.每根桩柱采用离散为1 m的单元，约束混凝土和非约束混凝土采用Opensees中提供的“Concrete02”材料[22]模拟，抗压强度取为32.4 MPa，约束混凝土的本构关系采用Mander模型[23]，钢筋采用Opensees中的“Steel02”材料[22]模拟，抗拉强度取为335 MPa.基础对桩柱的约束采用动力p-y法[18]分别考虑的基础对桩柱的侧向、竖向和桩端的约束，假定土层材料均为中砂.为了考虑冲刷效应，移除冲刷后土层对桩柱的约束作用.

4.2计算结果

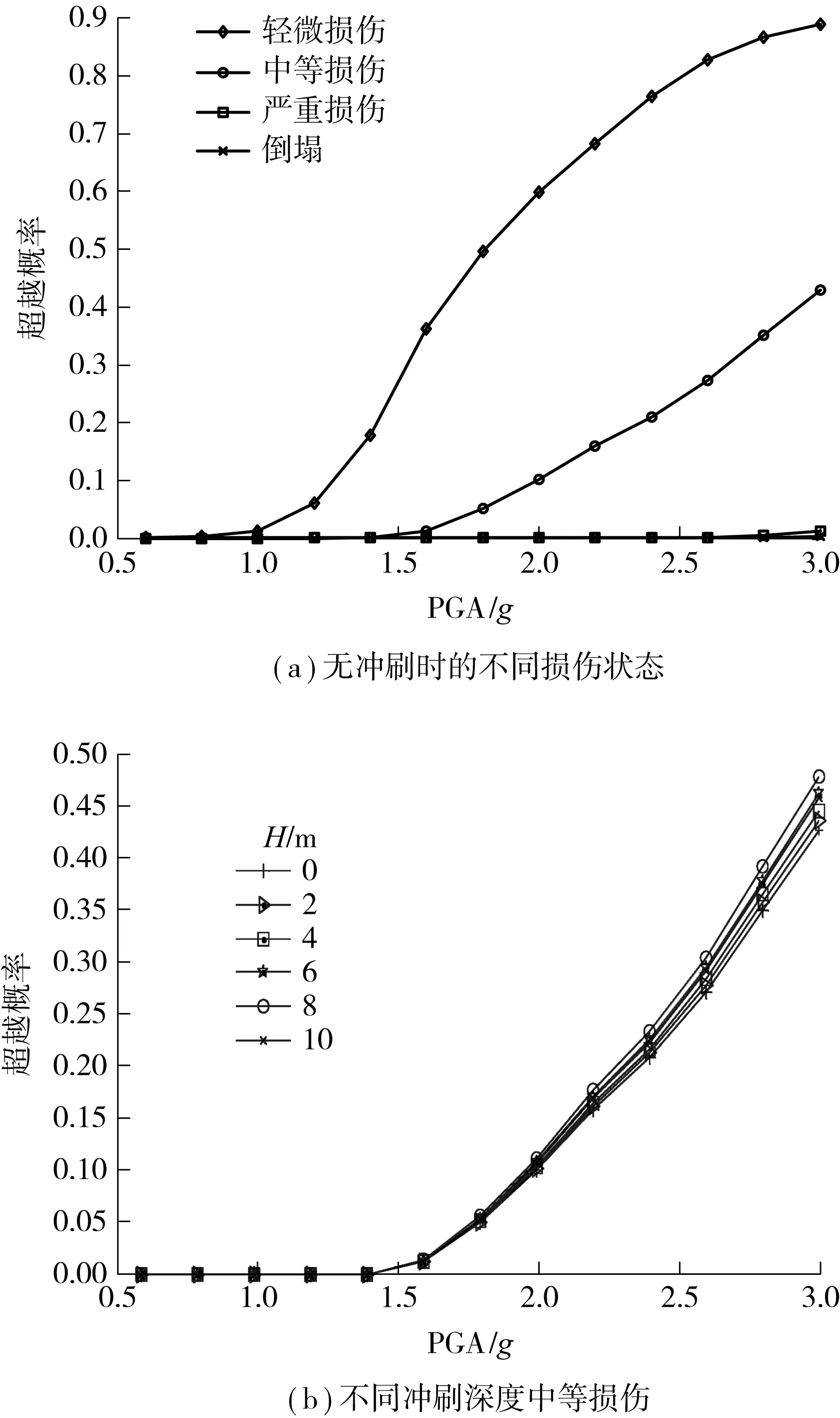
图4　无冲刷时不同损伤状态和不同冲刷深度中等损伤的易损性曲线Fig.4　Fragility curves of four damage levels without scouring and the 2nd damage level for different scour depth

根据计算结果，综合考虑桥塔的各截面以及桩柱截面、桥塔塔底截面和桩柱承台底截面为地震荷载下最不利截面，桩柱承台底截面各损伤状态概率明显小于塔底.根据结构不同损伤等级的定义，得到塔底截面4种损伤状态的易损性曲线，如图4(a)所示.计算结果表明，塔底截面主要受到轻微损伤和中等损伤，严重损伤以及倒塌状态的损伤概率接近于0.综合考虑结构性能及其对使用功能的影响，以塔底中等损伤作为结构失效状态.塔底截面在不同冲刷深度下的失效超越概率如图4(b)所示，可以看出，随着冲刷深度的增加，塔底截面发生损伤的概率的越来越大，当冲刷深度达到8 m左右时，损伤概率达到极大值，之后损伤概率呈现降低的趋势.说明冲刷条件对结构动力荷载下的损伤影响不能简单地按照最大冲刷深度考虑.

塔底截面在冲刷和地震两种灾害下的易损伤性曲面如图5所示，可以从易损性曲面明显看出，当冲刷深度为8 m时，发生损伤的概率最大.拟合易损面函数，可以得到联合失效概率JMAFP，通过对不同冲刷深度下塔底截面的易损性曲线积分，可以获得不同冲刷深度下塔底截面的失效概率MAFP_h，如图6所示.根据方程(14)，基于风险考虑多灾害下的合理设计冲刷深度Hr就是与JMAFP相同的MAFP_h所对应的冲刷深度，也就是图6中JMAFP与MAFP_h交叉点对应的深度.

图5　桥塔易损面Fig.5　Fragility surface of the tower

图6　联合失效概率和给定冲刷深度失效概率Fig.6　Joint failure probability and failure probability under a certain deterministic scour depth

根据冲刷危险性分析中提出的冲刷深度计算方法，按照百年一遇的洪水条件，计算得到文中桥塔的设计冲刷深度为Hd=7.62 m，基于风险的考虑冲刷和地震多灾害下的设计冲刷深度Hr=3.86 m，由方程(15)，冲刷荷载系数为γs=3.86/7.62=0.51.基于风险分析得到的设计冲刷深度与百年一遇的设计冲刷深度相比更小，文中条件下采取百年一遇的设计冲刷深度更加保守，但其他情况可能会偏于不安全，因为结构损伤超越概率有时会出现峰值，如文中冲刷深度在8 m时.

在实际桥梁评估过程中，应该在得到的合理冲刷深度(γsHd)下去验算桥梁的抗震能力.桥梁设计过程需要考虑的组合系数，根据以上分析方法对同类型桥梁进行分析，获得代表此类桥梁的组合系数，参与到荷载组合中对桥梁进行设计.文中只是针对影响较大的局部冲刷进行了分析，该方法要真正地用到桥梁的设计中去，还需要更精细化的分析.

5结语

当前对于冲刷问题，一般只是确定性地考虑最大冲刷深度，而冲刷本身并不是一种荷载，只有与其他荷载组合才对结构产生影响，所以桥梁结构的冲刷问题是一个多灾害问题，需要合理考虑联合灾害组合问题，特别是对于投资巨大、对交通网极为重要的特大跨度桥梁.文中基于一致风险原则，提出了桥梁在考虑冲刷和地震联合灾害条件下的分析框架，获得两种灾害分析中的组合系数.总结如下：

(1)提出了基于风险思想的桥梁多灾害分析框架，建立了当前在桥梁设计中处理地震和冲刷两种灾害下选择合理冲刷深度和组合系数的方法；

(2)通过考虑地震和冲刷灾害的随机性， 建立了多灾害下概率地震需求模型；

(3)以一大跨度自锚式悬索桥为例对以上方法进行了说明.根据桥梁特点及两种灾害的危险性分析，明确了桥梁的失效状态，评估了桥梁在联合灾害下的失效概率，并根据提出的框架得到了基于风险分析的合理设计冲刷深度.

文中说明了基于风险思想的联合灾害方法在桥梁设计和评估中的应用.对于未来大跨度桥梁的设计，除考虑地震条件下桥塔和桩基的抗震能力外，还需考虑其他构件在其他灾害下的破坏情况，并对各种损伤状态采用统一的风险指标来衡量，明确桥梁面对的各种灾害的概率模型，还原桥梁在自然界中面对的各种挑战，以其在基于性能设计的理论体系内实现桥梁的多灾害设计.

参考文献：

[1]AASHTO (2012). AASHTO LRFD bridge design specifications [S]. Washington D C:American Association of State Highway and Transportation Officials,2012.

[2]GHOSN M，MOSES F，Wang J. NCHRP report: design of highway bridges for extreme events [R]. Washington D C: Transportation research Board of the National Acade-mics,2003.

[3]KUMALASARI Wardhana，FABIAN C Hadipriono. Analy-sis of recent bridge failures in the United States[J]. Journal of Performance of Constructed Facilities,2003,17(3):144-150.

[4]BRUCE Ellingwood，DAVID Rosowsky. Combining snow and earthquake loads for limit states design [J]. Journal of Structural Engineering,1996,122(11):1364-1368.

[5]LEE Kyung Ho，ROSOWSKY David V. Fragility analysis of woodframe buildings considering combined snow and earthquake loading [J]. Structural Safety,2006,28(3):289-303.

[6]YIN Yue-Jun，LI Yue. Probabilistic loss assessment of light-frame wood construction subjected to combined seismic and snow loads [J]. Engineering Structures,2011,33(2):380-390.

[7]LEONARDO Duenas-Osorio，JAMIE E Padgett. Seismic reliability assessment of bridges with user-defined system failure events[J]. Journal of Engineering Mechanics,2011,137(10):680-690.

[8]PAOLO Gardoni，KHALID M Mosalam，ARMEN der Kiureghian. Probabilistic seismic demand models and fragility estimates for RC bridges [J]. Journal of Earthquake Engineering,2003,7(spec01):79-106.

[9]KEVIN R Mackie，BOžIDAR Stojadinovic′. R-factor parameterized bridge damage fragility curves[J]. Journal of Bridge Engineering,2007,12(4):500-510.

[10]JAMIE E Padgett，KRISTINA Dennemann，JAYADIPTA Ghosh. Risk-based seismic life-cycle cost-benefit (LCC-B) analysis for bridge retrofit assessment [J]. Structural Safety,2010,32(3):165-173.

[11]SUN Dezhang，SUN Baitao，LEE George C. Study on combination of internal forces on bridges subjected to earthquake and heavy trucks based on Ferry Borges theory [J]. Earthquake Engineering and Engineering Vibration,2011,31(6):18-23.

[12]SWAGATA Banerjee，GAUTHAM Ganesh Prasad. Seismic risk assessment of reinforced concrete bridges in flood-prone regions [J]. Structure and Infrastructure Engineering,2013,9(9):952-968.

[13]YOU Dong，DAN M Frangopol，DUYGU Saydam. Time-variant sustainability assessment of seismically vulnerable bridges subjected to multiple hazards [J]. Earthquake Engineering & Structural Dynamics,2013,42(10):1451-1467.

[14]ALIPOUR A，SHAFEI B，SHINOZUKA M. Reliability-based calibration of load and resistance factors for design of RC bridges under multiple extreme events: scour and earthquake [J]. Journal of Bridge Engineering,2012,18(5):362-371.

[15]焦驰宇. 基于性能的大跨斜拉桥地震易损性分析 [D]. 上海：同济大学,2008.

[16]冯清海. 特大桥梁地震易损性与风险概率分析 [D]. 上海：同济大学,2008.

[17]沈国煜，袁万城，庞于涛. 斜拉桥复合地震易损性分析 [J]. 同济大学学报(自然科学版),2013,41(7):970-976.

SHEN Guo-yu,YUAN Wan-cheng,PANG Yu-tao. Cable-stayed bridges seismic fragility analysis [J]. Journal of Tongji University (Natural Science),2013,41(7):970-976.

[18]WANG Zhenghua，LEONARDO Dueas-Osorio，JAMIE E Padgett. Seismic response of a bridge-soil-foundation system under the combined effect of vertical and horizontal ground motions [J]. Earthquake Engineering & Structural Dynamics,2013,42(4):545-564.

[19]ARNESO L A， ZEVENBERGEN L W，LAGASSE P F. Evaluating scour at bridges [R]. Washington D C: U.S. Department of Transportation Federal Highway Administration,2012.

[20]JOHNSON Peggy A，DOCK Daniel A. Probabilistic bridge scour estimates [J]. Journal of Hydraulic Engineering,1998,124(7):750-754.

[21]SAKAI Junichi，MAHIN S. Mitigation of residual displacements of circular reinforced concrete bridge columns[C]∥Proceedings of 13th World Conference on Earthquake Engineering. Vancouver:WCEE,2004:1-13.

[22]Opensees.Open system for earthquake engineering simu-lation [DB].Berkeley:Pacific Earthquake Engineering Research Center,University of California,2014.

[23]MANDER John B，PRIESTLEY Michael J N，PARK R. Theoretical stress-strain model for confined concrete [J]. Journal of Structural Engineering,1988,114(8):1804-1826.

Risk-Based Probe into Appropriate Scour Depth of Bridge Under Multiple Hazards

YANGYan-kaiMARu-jinCHENAi-rong

(Department of Bridge Engineering, Tongji University, Shanghai 200092,China)

Abstract:In order to guide the future design of new bridges or the assessment of existing ones, a multi-hazard design framework is proposed on the basis of risk-consistent design for bridges under earthquake and scour hazards, and the appropriate scour depth considering the earthquake is investigated.Firstly, a fragility analysis considering scour is carried out for the bridge under earthquake to obtain the fragility surface and fragility curve of the bridge.Secondly, two probabilistic risk models respectively corresponding to earthquake and scour hazards are proposed and are used to reveal the relationship between the failure probability under seismic hazard and the scour depth and to obtain the joint failure probability of the bridge.Then, the scour depth corresponding to joint failure probability is taken as the appropriate scour depth to make a comparison with the designed value, from which load combination factors for bridge design are determined.Finally, a case study on a suspend bridge is carried out.The results show that the proposed method effectively considers both bridge risk and economy, so that it lays a foundation for exploring the combined action of earthquake and scour hazards for bridges with different types and scales.

Key words:bridge;risks; earthquakes; scour; multiple hazard

收稿日期：2015- 05-11

*基金项目：“十二五”交通运输部重大科研专项(2011318494160)

Foundation item:Supported by the “Twelfth Five Year Plan”Major Scientific and Technological Special Project of Ministry of Transport of China (2011318494160)

作者简介：杨延凯(1984-)，男，博士生，主要从事桥梁设计理论研究.E-mail:yangyankai2014@126.com

中图分类号：U441

doi：10.3969/j.issn.1000-565X.2016.03.015