带状态变量约束的自动变速器正转矩降挡控制*

叶杰　 黄向东　 赵克刚　 何小鹏　 刘延伟

(1.华南理工大学 广东省汽车工程重点实验室, 广东 广州 510640; 2.广东工业大学 机电工程学院, 广东 广州 510006)

带状态变量约束的自动变速器正转矩降挡控制*

叶杰1黄向东1赵克刚1何小鹏1刘延伟2

(1.华南理工大学 广东省汽车工程重点实验室, 广东 广州 510640; 2.广东工业大学 机电工程学院, 广东 广州 510006)

摘要：以单摩擦元件搭接控制动力换挡式自动变速器为例,分析了自动变速器正转矩降挡动力学过程,制定了摩擦元件与动力源转矩间的协调控制策略.以滑摩功与惯性相结束了时刻点的冲击度构造目标泛函,基于极小值原理对动力源转矩受限条件下的降挡过程惯性相进行协调控制优化.以动力源、摩擦元件转矩变化率为双控制变量,引入状态变量、控制变量的不等式约束条件,通过对该带约束条件波尔扎问题的数值求解确定惯性相最优状态变量轨迹曲线.仿真与台架试验结果表明,该方法有效减小了变速器输出轴的转矩波动,提升了动力性,改善了换挡品质.

关键词：自动变速器；降挡过程；不等式约束；极小值原理；协调控制策略

汽车自动变速器动力换挡过程中摩擦元件与动力源转矩间的协调控制,是自动变速器控制的关键技术,对车辆性能具有重要的影响[1-2].随着自动变速器电控技术的进步,国内外学者针对自动变速器升挡与起步控制策略开展了深入的研究[3- 4],提出了基于多目标遗传算法[5]、动态规划法[6]、模糊控制[7]、线性化控制[8]、线性二次型最优控制算法[9-10]等的多种控制方案.而与升挡过程的动力学特性相比,正转矩降挡过程有其特殊性.在正转矩降挡过程中,动力源转矩水平较高,升扭辅助控制受到了系统的极限能力的限制,若控制策略的制定中不考虑状态变量(动力源转矩)的约束,则无法在实际对象中获得应用.正力矩降挡优化控制问题本质上是一个带状态变量、控制变量不等式约束条件的波尔扎问题[11].文中拟应用现代变分法两大基石之一的极小值原理来解决以上问题.

在新兴的电动汽车变速传动领域,国内外专家推荐采用两档变速器来改善车辆的动力性与经济性[12].电动汽车两档变速器高、低挡之间的速比级差越大,动力系统的响应要求越快,整车轻量化的要求也越紧迫.为满足对电动汽车专用两挡变速器的更高要求,基于摩擦元件-开关元件搭接换挡机理,Sorniotti等[13]提出了一种以摩擦片式离合器与单向离合器搭接控制的两挡自动变速器.高炳钊等[14]提出了一种以摩擦片式离合器与同步器搭接控制的两挡AMT传动结构.赵克刚等[15]提出了一种两挡无动力中断手动操纵机械式变速器方案.摩擦元件与开关元件搭接换挡方式利用开关元件(单向离合器、啮合套、犬牙式离合器)替换传统多摩擦元件变速器(如DCT、AT等)中的部分摩擦元件(离合器或制动器),可以简化变速器的结构和减小变速器尺寸,并且通过摩擦元件与开关元件间的搭接可以实现动力换挡(换挡过程无动力中断).

文中以电动汽车带两挡摩擦元件-开关元件搭接自动变速器的降挡过程为研究对象,在惯性相中构造了兼顾同步时刻点的冲击度和滑摩功的目标泛函,同时引入状态、控制变量的不等式约束条件,基于极小值原理对动力源转矩受限条件下的降挡过程惯性相协调控制进行优化;将数值计算得到的最优控制变量曲线应用于降挡过程的仿真与试验,以验证该优化方法的可行性.

1正转矩降挡过程分析

搭接控制换挡方式可分为双摩擦元件搭接和摩擦元件-开关元件搭接控制.这两种换挡方式的换挡动力学方程基本相同[9,13-15].正转矩降挡过程中首先进入惯性相,待低挡换挡元件进入结合状态后转入转矩相,高挡换挡元件完全脱开后进入低挡位传动状态.

1.1正转矩降挡机理

图1为某电动汽车带两挡摩擦元件-开关元件搭接自动变速器的简化集中惯量动力学模型.其基本结构由1个摩擦元件及其执行机构、1个开关元件及其执行机构、齿轮传动构成,通过摩擦元件与开关元件间的搭接控制即可完成动力换挡.采用该简化模型,有利于减小最优控制问题的求解规模.

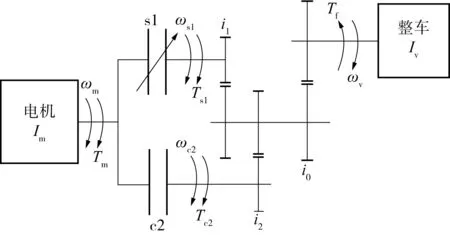
图1　传动系统的简化模型Fig.1　Simplified model of driveline system

如图2所示,降挡过程首先进入惯性相,开关元件s1保持分离状态,不传递转矩,摩擦元件c2分离至滑摩状态,同时对电机转矩进行调整,尽快使电机转速ωm由c2从动部件转速ωc2升高至s1从动部件转速ωs1;当s1结合后进入转矩相阶段,电机输出转矩逐渐从离合器传递切换至开关元件传递,随着c2传递转矩逐渐下降,s1传递转矩逐渐上升,直至c2传递转矩下降为0时转矩相结束;最后,电机转矩逐渐恢复至驾驶员所需求的转矩水平(转矩恢复阶段).图2中的t1、t2、t3、t4分别为惯性相开始时刻、惯性相结束时刻、转矩相结束时刻、转矩恢复阶段结束时刻.

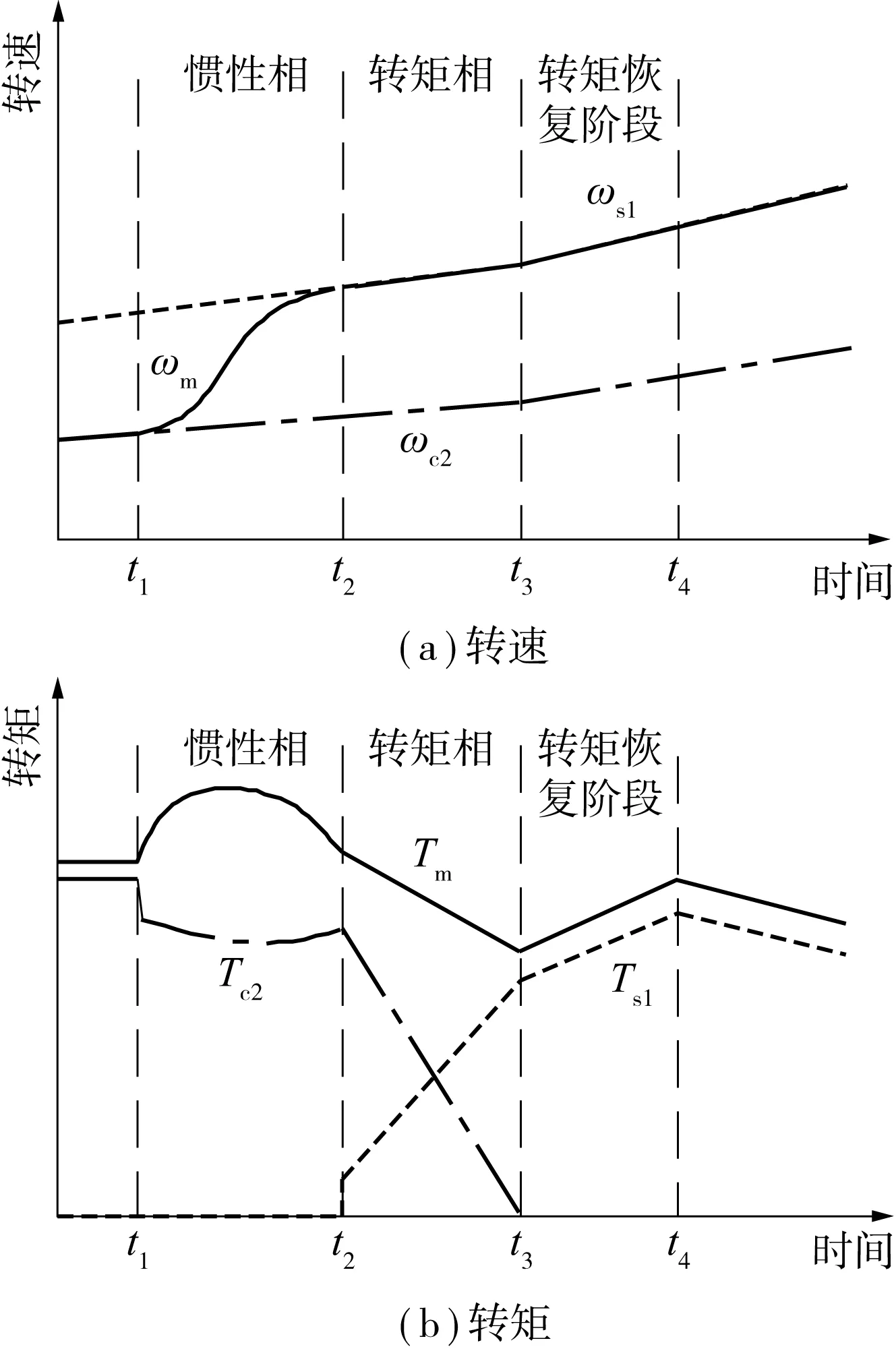
图2　正转矩降挡过程的特性曲线Fig.2　Characteristic curves of positive-torque downshift process

正转矩降挡过程中转矩恢复阶段采取何种策略,应考虑摩擦元件-摩擦元件或摩擦元件-开关元件搭接换挡方式中待接合元件促动装置特性的不同和司机的驾驶需求.限于篇幅,转矩恢复阶段的控制策略非文中的重点阐述内容.

1.2正转矩降挡的动力学方程

正转矩降挡过程中,传动系统的动力学方程为

(1)

(2)

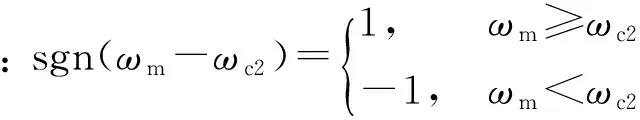
在一、二挡行驶阶段(含转矩恢复阶段),传动系统的动力学方程为

(3)

式中：k=1,2.

2控制策略

文中在惯性相中采用极小值原理开展带状态变量、控制变量不等式约束的电机、摩擦元件转矩间的协调控制研究.在转矩相中,文中参考文献[14]采取开环线性控制策略,该策略可控制电机、摩擦元件的转矩,在满足冲击度要求的条件下减小滑摩功.

2.1惯性相

2.1.1最优控制问题描述

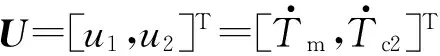
(4)

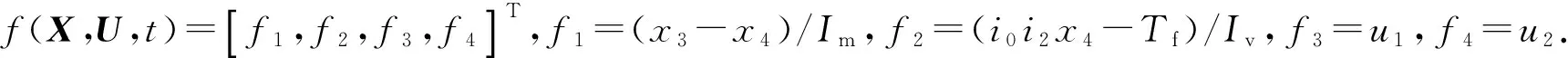
以惯性相结束时刻开关元件s1由分离状态切换至结合状态引起的冲击度与滑摩功作为优化目标,建立目标泛函:

(5)

惯性相结束时刻的冲击度jt2为

(6)

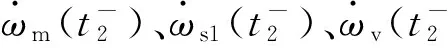
滑摩功W为

(7)

为了保证正转矩降挡过程中冲击度j的幅值小于标定的容许冲击度,并考虑电机控制系统所能实现的电机极限控制电流,设控制变量的不等式约束条件为

(8)

式中,u1max为电机控制系统确定的电机转矩最大变化率幅值,u2max为由正转矩降挡过程中容许冲击度确定的最大摩擦元件转矩变化率幅值.

在正转矩降挡过程中电机的转矩水平较高,升扭辅助控制受到电机转矩上限的限制,因此针对状态变量(电机转矩)施加不等式约束条件为

x3(t)≤g(x1)

(9)

式中,g(x1)为对应电机转速的电机所能输出的最大转矩值.

惯性相结束时刻s1的主、从动部件转速同步构成了终了时刻的状态变量的约束条件:

ψ(X(t2),t2)=x1(t2)-i0i1x2(t2)=0

(10)

2.1.2最优控制问题求解

为了将状态变量的不等式约束条件转换为等式约束条件,定义一个新的状态变量x5,使其满足:

(11)

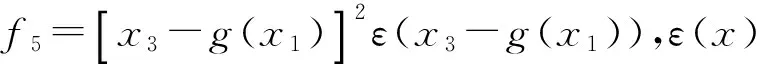
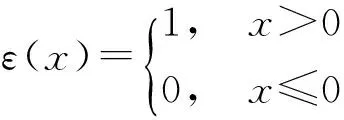
(12)

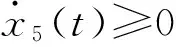
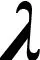
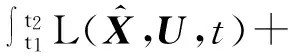
(13)

根据极小值原理可得Hamilton函数为

(14)

控制方程为

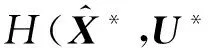
(15)

则最优控制变量为

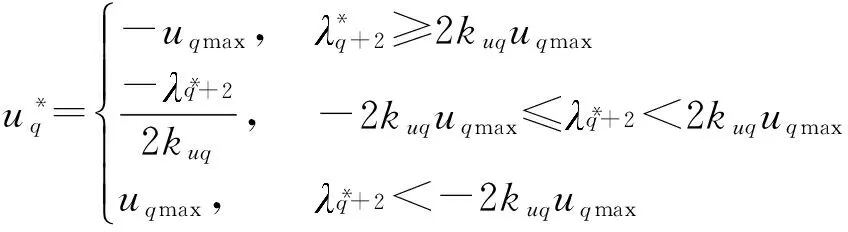
(16)

式中,q=1,2.

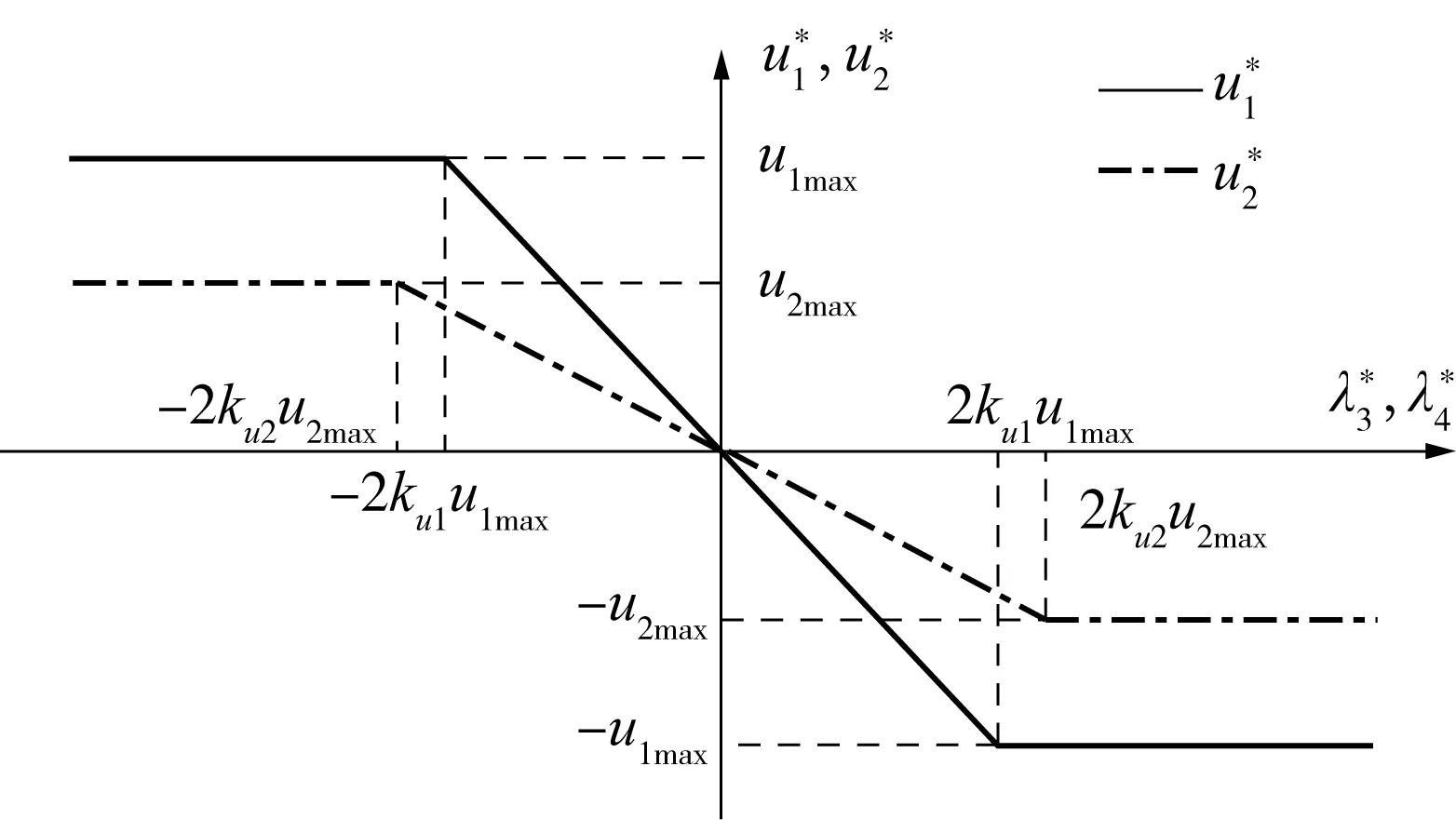
图3　最优控制变量与最优协状态变量的关系图Fig.3　Relational graph of optimal control and state variables

状态方程为

(17)

协状态方程为

(18)

初始条件、约束条件、横截条件为

(19)

(20)

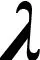
(21)

(22)

式中,ωm(t1)、ωv(t1)分别为惯性相开始时刻电机、变速器输出轴的转速,Tm(t1)、Tc2(t1)为惯性相开始时刻电机、摩擦元件的转矩.

联立求解式(15)-(22),可得到带状态、控制变量不等式约束条件下的最优状态变量轨迹.

2.2转矩相

在转矩相中,开关元件s1保持结合状态,其主、从动部分转速相等,可得到转矩相下系统动力学方程为

(23)

由式(1)、(2)、(23)可知,转矩相中s1的传递转矩为

(24)

由式(24)可知,在转矩相中,s1传递转矩并不是一成不变的.随着c2逐渐分离,s1传递转矩逐渐上升,电机输出动力流逐渐由c2所在二挡传递回路切换至s1所在一挡传递回路输出至车轮.

由式(23)可知,转矩相中冲击度为

(25)

由式(25)可知,转矩相中的冲击度由电机、摩擦元件转矩的导数共同决定.基于上述耦合关系,依据文献[14],文中在转矩相中以摩擦元件执行机构限制的最大分离速率分离摩擦元件,离合器分离过程中辅以电机降矩,使转矩相中在满足冲击度要求下尽快结束转矩相,减小滑摩功.转矩相结束后,逐渐恢复电机转矩至驾驶员需求的转矩值(转矩恢复阶段).

3仿真结果分析

根据所建立的自动变速器降挡过程动力学模型及电机协调控制策略,在Matlab/Simulink软件平台上对所制定的电机协调控制策略进行仿真分析.

3.1惯性相最优控制分析

以某型号电动汽车[9]为研究对象,针对降挡过程惯性相中的状态变量施加不等式约束(策略1)与未施加不等式约束(策略2)的最优控制问题进行数值求解,主要输入参数如下:整车质量m=1 450 kg,车轮半径Rw=0.22 m,一挡速比i1=2.7,二挡速比i2=1.4,主减速比i0=4.1,空气阻力系数CD=0.36,迎风面积A=2.08 m2,地面摩擦阻力系数f=0.010 3,电机等效转动惯量Im=0.18 kg·m2,电机额定输出最大转矩Tmax=200 Nm,电机额定基速为2 400 r/min.

两种策略下的最优状态轨迹如图4所示.从图中可知,状态轨迹变化趋势是一致的:电机转速从与摩擦元件同步的当前挡位转速升高至与开关元件同步的目标挡位转速值;摩擦元件转矩先以容许冲击度限定的最大转矩变化率下降,而后摩擦元件转矩导数由负值逐渐转为正值,最后以容许冲击度限定的最大转矩变化率上升;电机转矩变化趋势与摩擦元件相似,先升高后下降.上述状态变量轨迹保证了开关元件主、从动部分转速迅速同步,并减小了同步时刻开关元件主、从动部分的角加速度的差值,抑制了由开关元件状态切换引起的冲击.

图4 　惯性相的最优轨迹Fig.4　Optimized trajectories of the inertia phase

由图4(c)可以看出:状态变量不等式约束可以使电机在其转矩达到上限时稳定工作在边界;未对状态变量施加不等式约束时,电机转矩会超出其极限能力,这与实际情况相悖.

3.2降挡过程仿真分析

选取3.1节的电动汽车为仿真对象.该车在坡度为14%的道路上以15 km/h行驶,加速踏板开度为70%.司机为尽快超越前车,通过换挡杆发出降挡指令.根据前面制定的协调控制策略对搭建的降挡动力学仿真模型进行仿真控制研究.正转矩降挡控制过程的仿真结果如图5所示.

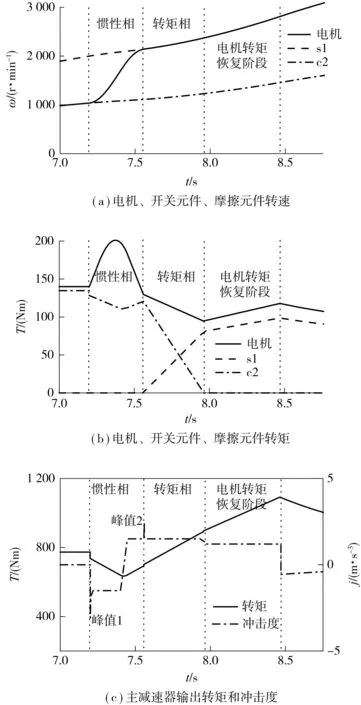
图5　正转矩降挡过程仿真结果Fig.5　Simulation results of the positive-torque downshift process

由图5(a)、5(b)可知:在惯性相阶段,开关元件s1传递的转矩仍然为0,为了尽快实现s1的主、从动部分的转速同步并减小惯性相终了时刻的冲击,可根据3.1节的最优控制轨迹对电机、摩擦元件转矩进行控制;进入转矩相后,c2传递的转矩逐渐下降,s1传递的转矩同步上升,辅以2.2节制定的电机辅助降矩控制策略,可以保证冲击满足要求.

在转矩恢复阶段,电机转矩逐渐恢复至驾驶员加速踏板所对应的转矩水平,此时车辆冲击度与电机转矩的变化率成正比,加速踏板开度越大,所设定的转矩切换速度越大,相应的冲击度也越大.换挡结束后电机力矩指令已交还驾驶员加速踏板,随着电机转速逐渐升高至高于基速,电机特性位于恒功率区域,随着电机转速上升,电机输出转矩有所下降.

如图5(c)所示,降挡过程中冲击度满足小于10 m/s3的要求[15],其冲击度曲线在第7.20秒和第7.56秒出现两个脉冲峰值,峰值1是由惯性相开始时刻摩擦元件静、动摩擦状态切换引起的负冲击,具体数值取决于摩擦片的材料特性.峰值2是由惯性相结束时刻开关元件自分离状态切换至结合状态所引起的冲击,经优化控制后得到有效的抑制.整个降挡滑摩功为5.07 kJ,对比文献[16]中的单离合器起步仿真结果(5.148 kJ),该值完全可以被接受;换挡前主减速器输出转矩为773 Nm,转矩相结束时输出转矩为893 Nm,转矩恢复阶段结束时输出转矩为1 091 Nm,通过降挡动作,有效地提升了车辆行驶动力性.整个降挡过程中车速变化比较平稳,换挡平顺性好.

4降挡台架试验研究

为验证所提出的摩擦元件-开关元件搭接正转矩降挡过程中协调控制策略的有效性,文中在由三相异步电机、磁粉离合器(摩擦元件)、单向离合器(开关元件)、一及二挡动力回路、大惯量负载飞轮组成的换挡试验台架上进行降挡试验研究.试验台架原理及现场布置如图6所示.

图6　换挡传动试验台架Fig.6　Transmission test bench of shift

上述摩擦元件-开关元件搭接控制换挡试验台架通过色标转速传感器采集转速信号,通过转矩转速传感器采集变速器输出轴转矩.工控机对采集信号进行数据分析,并通过变频器及程控电源对电机、磁粉离合器转矩进行控制.电机、磁粉离合器转矩采取转矩协调控制前、后的降挡试验结果如图7所示.

从图7可知,与未采取电机转矩协调控制策略相比,采用转矩协调控制策略后惯性相阶段的持续时间由0.45 s缩短为0.30 s,整个过程的变速器输出轴转矩波动更小,惯性相同步时刻由单向离合器分离至结合状态切换引起的角冲击度由46.7 rad/s3减小至13.1 rad/s3,幅值减小了71.9%,整个过程的冲击度得到了有效的控制.观察图7(b)中16.4～17.3 s间的输出转矩曲线发现,换挡过程中输出端力矩在上升的同时存在周期性波动.该振动的频率与幅值由传动系统的刚度、阻尼特性决定,对换挡过程中的冲击度产生一定的影响.另外,从台架试验结果可知,电机及摩擦元件转矩控制能够满足转矩协调控制的需求.

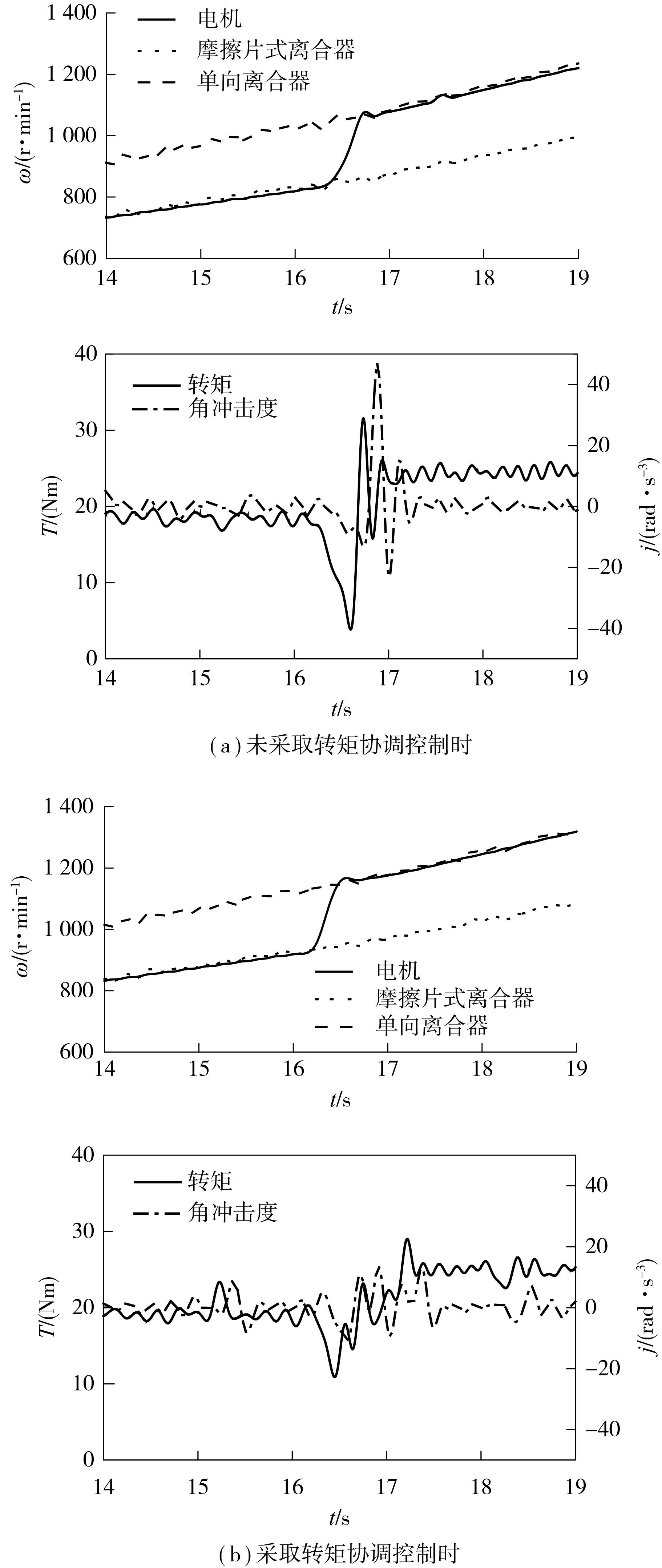
图7　转矩协调控制前、后的降挡试验结果Fig.7　Test results of downshift with or without the cooperative control

5结论

(1)对于动力换挡式自动变速器正转矩降挡过程,当考虑电机最大输出转矩的限制时,可采用极小值原理解决惯性相带状态变量不等式约束的自由边界最优控制问题,有助于克服传统控制策略的局限性.

(2)在仿真与台架试验中,将基于简化后的集中惯性动力学模型的最优协调控制策略所得到的电机、摩擦元件转矩变化率曲线对换挡过程进行控制,结果表明,该优化方法能在保证离合器寿命的前提下提高行驶平顺性,减小换挡过程中的冲击,从而验证该优化方法在改善换挡性能方面的可行性及有效性.

(3)系统刚度阻尼特性对换挡过程中的冲击度有一定的影响,完善文中传动系统的动力学模型是今后进一步的研究方向.文中研究的带状态变量、控制变量的不等式约束条件波尔扎问题不仅局限于纯电动汽车,也适用于在传统内燃机车辆中普遍采用的基于双摩擦元件搭接换挡方式的自动变速器的换挡过程.

参考文献：

[1]GEOTZ M,LEVESLEY M C,CROLLA D A.Dynamics and control of gearshifts on twin-clutch transmissions [J].Journal of Automobile Engineering,2005,219(8):951-963.

[2]万国强,黄英,张付军,等.自动变速器升挡过程惯性相发动机协调控制 [J].机械工程学报,2012,48(16):91-96.

WANG Guo-qiang,HUANG Ying,ZHANG Fu-jun,et al.Coordinated engine control for automatic transmission du-ring the inertia phase of upshifting [J].Journal of mecha-nical Engineering,2012,48(16):91-96.

[3]KULKARNI M,SHIM T,ZHANG Y.Shift dynamics and control of dual-clutch transmission [J].Mechanism and Machine Theory,2007,42(2):168-182.

[4]WU Mingxiang,ZHANG Jianwu,LU Tongli,et al.Research on optimal control for dry dual-clutch engagement during launch [J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2010,224(6):749-763.

[5]宋勇道.基于两挡双离合器自动变速器的纯电动汽车驱动与换挡控制技术研究 [D].长春:吉林大学,2013:59-72.

[6]严忆泉,宋键,李亮.干式双离合自动变速器分段优化换挡策略研究 [J].农业机械学报,2014,45(5):30-36.YAN Yi-quan,SONG Jian,LI Liang.Multi-section optimization shift control method of dry clutch transmission [J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(5):30-36.

[7]秦大同,赵玉省,胡建军,等.干式离合器系统换挡过程控制分析 [J].重庆大学学报(自然科学版),2009,32(9):1016-1023.

QIN Da-tong,ZHAO Yu-sheng,HU Jian-jun,et al.Analysis of shifting control for dry dual clutch system [J].Journal of Chongqing University(Natural Science Edition),2009,32(9):1016-1023.

[8]ZHAO Kegang,LIU Yanwei,HUANG Xiangdong,et al.Uninterrupted shift transmission and its shift characteri-stics [J].Transactions on Mechatronics,2014,19(1):374-383.

[9]GAO Bingzhao,XIANG Yu,CHEN Hong,et al.Optimal trajectory planning of motor torque and clutch slip speed for gear shift of a two-speed electric vehicle [J].Journal of Dynamic Systems,Measurement,and Control,2015,137:061016/1-9.

[10]GU Qiang,CHENG Xiusheng.Study on double-clutch transmission gear shift control based on optimal theory [C]∥Proceedings of 2011 IEEE the 18th International Conference on Industrial Engineering and Engineering Management.Changchun:IEEE,2011:629- 634.

[11]HARTL R F,SETHI S P,VICKSON R G.A survey of the maximum principles for optimal control problems with state constraints [J].SIAM Review,1995,37(2):181-218.

[12]郭孔辉,姜辉,张建伟.电动汽车传动系统的匹配及优化 [J].科学技术与工程,2010,10(16):3892-3896.

GUO Kong-hui,JIANG Hui,ZHANG Jian-wei.Power- train matching and optimization of electric vehicles [J]. Science Technology and Engineering,2010,10(16):3892-3896.

[13]SORNIOTTI A,HOLDSTOCK T,PILONE G L,et al.Analysis and simulation of the gearshift methodology for a novel two-speed transmission system for electric power-trains with a central motor [J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2012,226(7):915-929.

[14]GAO Bingzhao,LIANG Qiong,XIANG Yu,et al.Gear ratio optimization and shift control of 2-speed I-AMT in electric vehicle [J].Mechanical Systems and Signal Processing,2015,50/51:615- 631.

[15]赵克刚,姚伟浩,刘延伟,等.一种纯电动汽车动力换挡式机械变速器 [J].中国机械工程,2015,26(12):1697-1703.

ZHAO Ke-gang,YAO Wei-hao,LIU Yan-wei,et al.A study of power shift mechanical transmission for pure electric vehicle [J].China Mechanical Engineering,2015,26(12):1697-1703.

[16]吴光强,司建玉.双离合器自动变速器起步的智能控制策略 [J].同济大学学报(自然科学版),2012,40(1):81-87.

WU Guang-qiang,SI Jian-yu.Launching intelligent control strategy for dual clutch transmission [J].Journal of Tongji University(Natural Science),2012,40(1):81-87.

责任编辑：许花桃

Control of Positive-Torque Downshifting Process of Automatic Transmission with State Variable Constraints

YEJie1HUANGXiang-dong1ZHAOKe-gang1HEXiao-peng1LIUYan-wei2

(1. Guangdong Key Laboratory of Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China;2. School of Electro-Mechanical Engineering, Guangdong University of Technology, Guangzhou 510006, Guangdong, China)

Abstract:By taking an automatic transmission that implements the power shifting only with a single friction clutch as the research objective, the dynamic process of positive-torque downshifting of automatic transmission is analyzed to establish a coordination control strategy for friction clutch and engine torque. By considering the jerk at the end of the inertia phase and the friction work as the comprehensive objective functional, the coordination control is accomplished on the basis of minimum principle, which is used to optimize the inertia phase in downshifting process with torque constraints. Moreover, by taking the gradient of the power source torque and the friction clutch as two control variables and by applying the inequality constraints on control variables and state variables, the constrained Bolza problem is solved numerically and the optimal state variables’ trajectory is obtained. Simulation and bench test results indicate that the proposed method effectively decreases the torque fluctuation of transmission output shaft, promotes the dynamic property and improves the shift quality.

Key words:automatic transmission; downshifting process; inequality constraint; minimum principle; coordination control strategy

收稿日期：2015- 07-10

*基金项目：国家自然科学基金资助项目(51575189);华南理工大学中央高校基本科研业务费专项资金资助项目(2015ZZ086)

Foundation item:Supported by the National Natural Science Foundation of China(51575189)

作者简介：叶杰(1991-),男,博士生,主要从事车辆系统动力学和自动变速器理论研究.E-mail:452016239@qq.com † 通信作者： 赵克刚(1977-)，男，博士生，副教授，主要从事车辆传动与电动汽车理论研究. E-mail:kgzhao@scut.edu.cn

中图分类号：U461.6

doi：10.3969/j.issn.1000-565X.2016.03.009