Heston模型下最优投资-消费策略选择

杨　鹏

(西京学院 应用统计与理学系　陕西 西安 710123)



Heston模型下最优投资-消费策略选择

杨鹏

(西京学院 应用统计与理学系陕西 西安 710123)

摘要：在随机金融市场模型中，研究了最优投资-消费策略选择问题.随机金融市场由无风险资产和风险资产构成，在风险资产的方差满足Heston模型下，求得最优投资-消费策略最大化终端财富和累积消费的期望折现效用.在幂效用函数情形下，通过求解值函数满足的Hamilton-Jacobi-Bellman (HJB)方程，得到了最优投资-消费策略以及值函数的显式解.

关键词：Heston模型； HJB方程； 幂效用； 投资策略； 消费策略

0引言

应用随机控制理论研究最优投资-消费策略选择是数理金融中的一个热点问题[1—4].文献[1]首次研究了投资-消费问题，假设投资者的资产可以在消费和投资之间进行分配，目标是在时间区间[0,T]或[0,∞)上寻求最优的投资-消费策略和值函数的显式解.文献[2]研究了不完备市场上的投资-消费问题.文献[3]研究了财富有限制情形的投资消费问题.文献[4]研究了带比例交易费用的投资-消费问题.文献[5]研究了投资-消费问题，假设在金融市场上含有多个风险资产，给出了比较好的数值解.文献[6]应用随机脉冲理论研究投资-消费问题.上述对最优投资-消费问题的研究，都假设金融资产满足Black-Scholes模型，很多学者在研究最优投资问题时都对Black-Scholes模型进行了推广.文献[7]研究了CEV模型下基于确定缴费型养老金的最优投资.文献[8] 在O-U模型下，研究了基于确定缴费型养老金的最优投资.文献[9]在Heston模型下基于确定缴费型养老金的最优投资.文献[10]在Heston模型下研究了保险公司的最优投资和再保险，文献[11]在Ho-Lee利率模型下研究了最优投资-消费问题.本文致力于研究Heston模型下，最优投资-消费策略选择问题.关键是求解值函数满足的HJB方程，根据边界条件构造了解的形式，求得值函数和最优投资-消费策略的显式解.

1市场模型

假设所有的随机变量和过程都定义在完备的概率空间(Ω,F,P),满足Ft右连续且P-完备.假设没有交易费用，资产是无穷可分的，在概率空间(Ω,F,P)上定义两个标准布朗运动W1(t)和W2(t)，两个标准布朗运动的相关系数为ρ，即t=ρt.

一个金融市场由两个金融资产组成：一个是无风险资产(债券)，时刻t的价格为Bt；另一个为风险资产(股票)，时刻t的价格记为S(t).Bt满足方程dBt=rBtdt，这里常数r>0为无风险资产的利率，B0=1.假设风险资产的收益和方差都是随机的，即S(t)满足下面的Heston模型

(1)

其中k是一个正常数，η(t)满足下面的CIR模型,

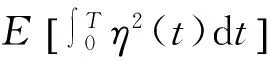
设时刻t在风险资产上的投资金额为π(t)，投资者的总财富为X(t)，则在无风险资产上投资的金额为X(t)-π(t).以c(t)表示投资者在t时刻的消费率，则考虑投资、消费后，财富过程X(t)满足下面的随机微分方程

(2)

定义1一策略θ(·)=(c(·),π(·))称为可行的，如果θ(·)关于流{Ft}是可料的，且对于任意时刻t≥0,过程θ(·)满足下面的条件：

3) 式(2)对于θ(t)有唯一的强解,所有可行策略记为Θ.

2Hamilton-Jacobi-Bellman(HJB)方程

假设投资者的目的是在区间[0,T]和最终时刻T最大化期望折现消费效用.记Vθ(t,η,x)是时刻t在投资-消费策略θ(t)=(c(t),π(t))和盈余为x，η(t)=η时的值函数，即

(3)

其中：u1(x)和u2(x)是2个二次可微、单调增加的凹的效用函数;a∈[0,1]为常数;参数β是折现率;u1(x)是度量消费的效用函数;u2(x)是度量最终财富的效用函数.本文假设消费效用和最终财富的效用是相互独立的,研究目标是寻找到值函数

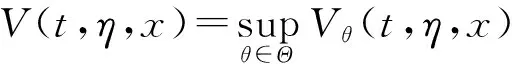
(4)

和最优的策略θ*使得

V(t,η,x)=Vθ*(t,η,x).

(5)

与文献[12—13]类似，应用随机控制理论，易得值函数V(t,η,x)满足下面的定理1和定理2.

定理1假设由(4)式，V关于变量t是连续可微的函数，同时关于x,η的二阶连续可微的函数，则V满足下面的HJB方程

ρσπ(t)η(t)Vxη+ae-βtu1(c(t))-c(t)Vx}=0,

(6)

边界条件

V(T,η,x)=(1-a)e-βTu2(x).

(7)

这里Vt、Vx、Vxx分别记作:V关于t的一阶导数，关于x的一阶导数，关于x的二阶导数，Vη、Vηη分别是关于η的一阶导数、二阶导数.

定理2设W∈C2是HJB方程(6)的解，是单调递减的凹函数，且满足边界条件式(7).则式(4)定义的V恰好等于W，进一步设θ*使下式成立,

ρσπ*(t)η(t)Vxη+ae-βtu1(c*(t))-c*(t)Vx=0,

则θ*(·)是最优策略，即W(t,x)=V(t,x)=Vθ*(t,x).(6)式在π*(t)、c*(t)处取得最大值，且满足下式

(8)

(8)式代入(6)式得

ae-βtu1(c*(t))-c*(t)Vx=0.

(9)

下面将求解(9)式，得到值函数的显式解，进一步得到最优投资-消费策略的显式解.

3最优投资-消费策略及值函数

引理1n(t)满足如下的Rieeati方程

(10)

则方程(10)的解为：

1) 当Δ>0时，

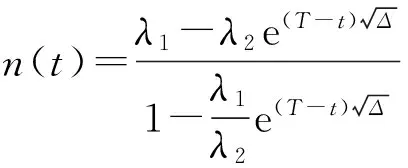
2) 当Δ=0时，

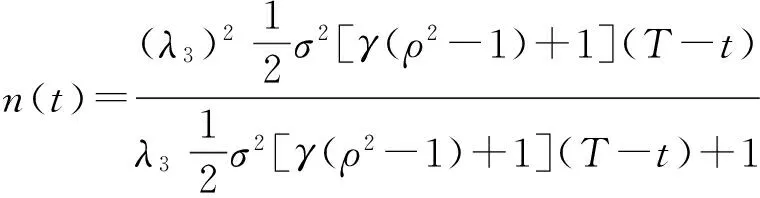
3) 当Δ<0时，

其中：

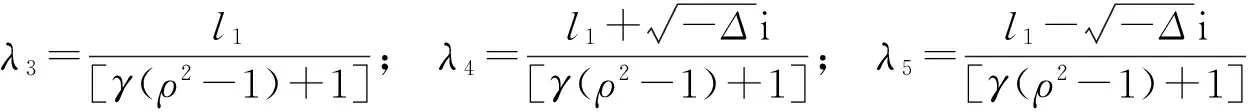
1) 当Δ>0时,方程(10)可变形为

(11)

(12)

式(12)两端在[t,T]上求积分，注意n(T)=0，即可求出n(t).

2) 当Δ=0时，方程(10)可变形为

(13)

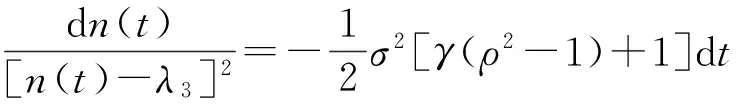
(14)

式(14)两端在[t,T]上求积分，注意n(T)=0，即可求出n(t).

引理2m(t)满足常微分方程

m′(t)+m(t)[l3+bn(t)]=0,m(T)=1,

(15)

则方程(15)的解为

引理3设

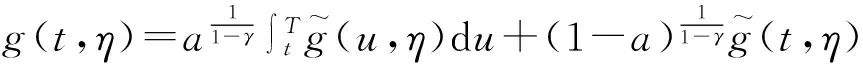
(16)

若g(t,η)∶=g满足方程

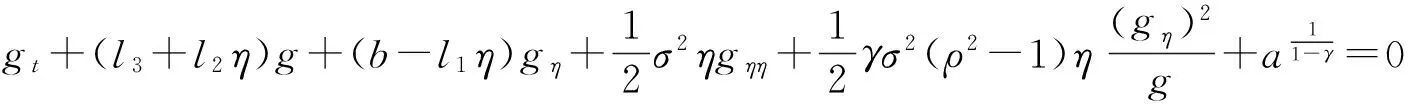
(17)

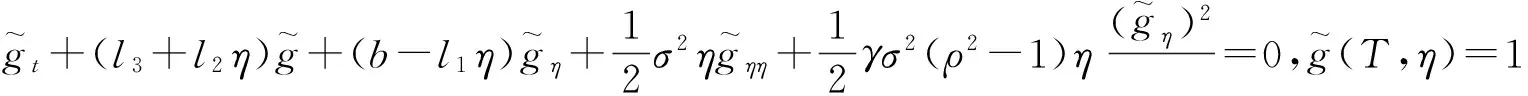
(18)

且

(19)

n(t)、m(t)分别满足引理1和引理2.

，

则(17)式可写为gt+.应用(16)式，(17)式可写成

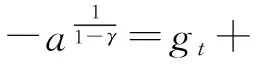
(20)

又因为

(21)

所以(20)式等于(21)，因此

也就是

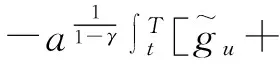
(22)

(23)

要使(23)式成立，则

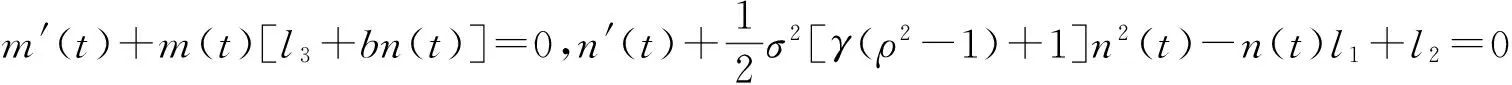
通过前面3个引理的准备，下面就可以求解方程(9)了,由边界条件式(7)，可设方程(9)有如下形式的解

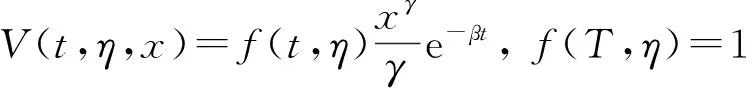
(24)

所以，有

代入方程(9)有

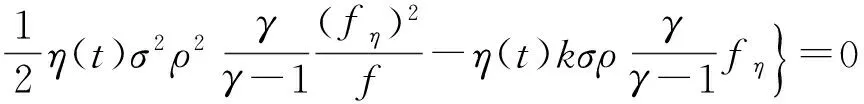
上式消除对x的依赖，得到

(25)

(25)式很难直接求解，需要进行转化，设

f(t,η)=[g(t,η)]1-γ,

(26)

所以

代入(25)式，得到

上式为零，即(17)成立，通过引理3即可求得g(t,η)，进一步就可以表示出V(t,η,x).

通过上述讨论，得到下面的定理.

定理3对于财富过程(2)最优的投资策略为

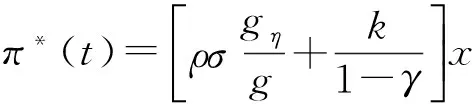
(27)

最优的消费策略为

(28)

相应的值函数为

(29)

其中：

n(t),m(t)分别满足引理1和引理2.

参考文献：

[1]METRO R C. Lifetime portfolio selection under uncertainty: the continuous time model [J]. The review of economics and statistics, 1969, 51(3): 247—257.

[2]COX J, HUANG C F. Optimal consumption and portfolio policies when asset prices follow a diffusion process [J]. Journal of economic theory, 1989, 49(1): 33—83.

[3]GROSSMAN S J, ZHOU Z. Optimal investment strategies for controlling draw downs [J].Mathematical finance , 1993, 3(3): 241—276.

[4]MAGILL M, CONSTANTINIDES G. Portfolio selection with transaction costs [J].Journal of economic theory, 1976, 13(2): 245—263.

[5]AKIAN M, MENALDI J, SULEM A. On the investment and consumption model with transaction costs [J]. Siam J Control Optimal, 1996, 34(1): 329—364.

[6]EASTHAM J, HASTINGS K. Optimal impulse control of portfolio [J]. Mathematics of operations research, 1988, 13(4): 588—605

[7]GAO J. Optimal portfolios for DC pension plans under CEV model[J]. Insurance mathematics and economics, 2009, 44(2): 479—490.

[8]谷爱玲，李仲飞，曾燕. Ornstein-Uhlenbeck模型下DC养老金计划的最优投资策略[J].应用数学学报, 2013, 36(4): 715—726.

[9]林祥，杨益非. Heston随机方差模型下确定缴费型养老金的最优投资[J].应用数学，2010, 23(2): 413—418.

[10]李艳方,林祥.Heston随机方差模型下跳-扩散风险模型的最优投资和再保险策略[J].经济数学，2009, 26(4): 32—41.

[11]常浩. Ho-Lee利率模型下带有零息票债券的投资-消费模型[J].中国管理科学, 2014, 22(10): 29—37.

[12]纪玉卿，曹玉松.投资收益下的再保险定价模型[J]. 信阳师范学院学报(自然科学版), 2008, 21(3): 358—360.

[13]王永茂，王丹，龙梅，等.跳-扩散风险模型下的最优投资和再保策略[J].郑州大学学报(理学版)，2015,47(1):50—54.

(责任编辑：方惠敏)

Optimal Investment-consumption Policies Selection for Heston Model

YANG Peng

(DepartmentofAppliedStatisticsandScience,XijingUniversity,Xi’an, 710123,China)

Abstract:The optimal investment-consumption policies selection problems were studied with stochastic financial market. In stochastic financial market, assets are composed of risk-free and risky asset, and the volatility of the risky asset was described by a Heston model. Optimal investment-consumption policies which maximize the expected discounted utility of terminal wealth and accumulative consumption was found. By solving the corresponding Hamilton-Jacobi-Bellman (HJB) equation, closed-form solutions for the value function as well as the investment-consumption policies in the power utility function case are obtained.

Key words:Heston model； HJB equation； Power utility； Investment policy； Consumption policy

收稿日期:2015-07-23

基金项目:陕西省教育厅专项科研计划项目(15JK2183).

作者简介:杨鹏(1983—)，男，山东临沂人，讲师，主要从事风险理论和数理金融的研究，E-mail:yangpeng511@163.com.

中图分类号：F830；O211.6

文献标志码：A

文章编号：1671-6841(2016)01-0017-06

DOI:10.3969/j.issn/1671-6841.201507035

引用本文:杨鹏.Heston模型下最优投资-消费策略选择[J]．郑州大学学报(理学版)，2016，48(1)：17—22.