基于PID和重复控制的三相四桥臂逆变器的研究

路　颜，　高锋阳，　张红生

(兰州交通大学 自动化与电气工程学院　甘肃 兰州 730070)



基于PID和重复控制的三相四桥臂逆变器的研究

路颜，高锋阳，张红生

(兰州交通大学 自动化与电气工程学院甘肃 兰州 730070)

摘要：在三相四桥臂逆变器被解耦成三个单相逆变器的基础上，提出了一种PID与重复控制相结合的控制策略.首先采用开关周期平均法和旋转坐标变换，建立旋转坐标系下的平均大信号模型，在此模型的基础上设计简单明了的PID控制器.其次对整个系统进行重复控制器的设计，居于外环的重复控制可以减小周期性扰动产生的畸变，提高系统的稳态性能.仿真结果表明,在不平衡负载和非线性负载情况下，逆变器都能够保持完好的电压输出特性和良好的动态特性.

关键词：三相四桥臂逆变器； 单相逆变器； PID控制； 重复控制； 解耦控制

0引言

与带分裂电容的三相四线逆变器、组合式三相四线逆变器和工频变压器隔离的三相四线逆变器等拓扑结构相比，三相四桥臂逆变器具有电路形式简单，质量小，体积小以及电压利用率高等优点[1].三相四桥臂逆变器输出电能质量主要取决于调制方法和控制器的设计[2].文献[3—4]采用三维空间PWM调制方法，该方法电压利用率高，开关频率较低，但是计算十分复杂.文献[5—6]采用特定谐波注入法，在一定程度上提高了电压利用率，但它更倾向于在电机驱动方面的应用，不太适合于不间断电源等逆变电源的控制.针对以上问题，本文将PID与重复控制相结合，应用到三相四桥臂逆变器的控制中，得到稳定的三相正弦输出电压，使系统具有良好的鲁棒性和动态特性.

1三相四桥臂逆变器的数学模型

图1　三相四桥臂逆变器的拓扑结构Fig.1　Topology of three-phase four-leg inverter

三相四桥臂逆变器的拓扑结构如图1所示.可以看出，三相四桥臂逆变器是在普通三相逆变器的基础上增加了一组臂对，该臂对的中点通过电感Ln与负载中性点连接在一起.Udc和ip分别表示直流母线电压与电流，ia、ib、ic和in表示流过各相滤波电感的相电流.Uag、Ubg、Ucg表示A、B、C各相的输出电压.Si(i=a+、a-、b+、b-、c+、c-、f+、f-)表示各个桥臂上开关管的开关函数，当Si=1时，表示此桥臂开通，反之，当Si=0时，表示此桥臂关断.依据开关周期平均法进行运算，得到各相电路的占空比为dag、dbg和dcg，根据电流回路分析可以得到

(1)

(2)

对各个输入变量、输出变量进行相对应的坐标变换:

(3)

式中:Ud、Uq、U0、id、iq、i0为在旋转坐标系下各相的相电压和相电流;dd、dq、d0为在旋转坐标系下各相的占空比.各个桥臂均已解耦，控制部分设计相对简单.0通道可以完全独立于其他两个通道进行设计，将d、q通道之间的耦合影响部分增添到扰动部分，得到系统在旋转坐标系下的平均大信号模型如图2所示.

2PID控制

PID控制具有结构简单、鲁棒性好且易于实现等优点.对三相四桥臂逆变器d轴和q轴的耦合项-ωLiq、ωLid、ωCUq和-ωCUd进行电压前馈解耦，得到旋转坐标系下PID控制的等效模型如图3所示.

图2　旋转坐标系下三相四桥臂逆变器的平均大信号模型

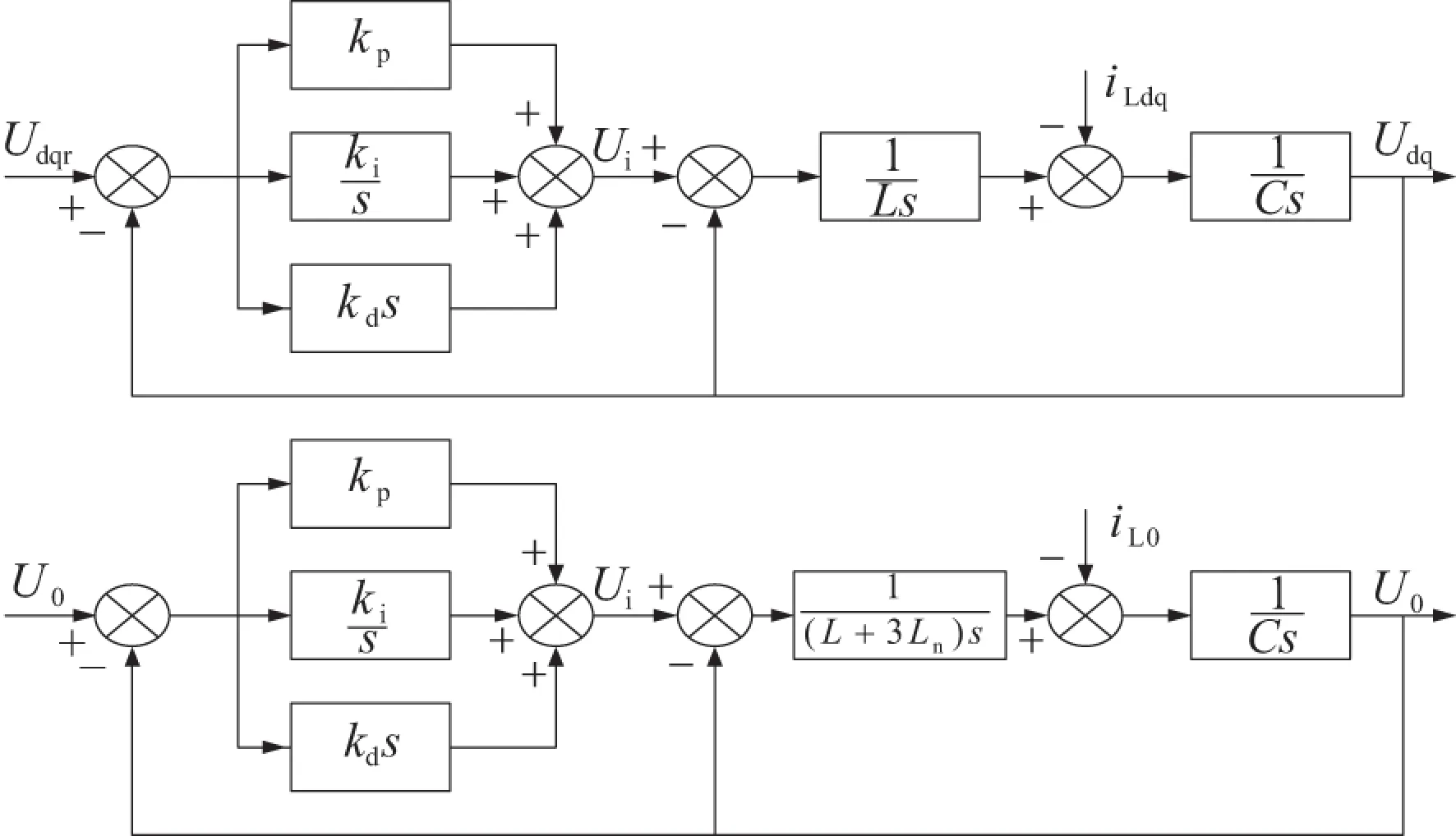
图3　旋转坐标系下PID控制的等效模型

可以看出，输入参考电压为Ur，负载电流的扰动信号为I0，得到整个系统的闭环传递函数为

(4)

该系统的闭环特征方程为

D(s)=LCs3+kds2+(1+kp)s+ki,

(5)

式中：kd、kp和ki分别表示PID控制中的比例、积分和微分参数；0轴时L=L+3Ln.

通过上述分析得知，整个控制系统是一个高阶系统，控制比较复杂.此系统的动态特性主要由主导极点决定，文献[7]详细介绍了极点配置过程，满足系统动态要求的参数为

(6)

式中：ζ=0.707，n=10，ω=5 000 rad/s，L=Ln=1.8 mH，C=30 μF.可以得到d、q轴的PID控制参数为kd=0.002 3，kp=13.846，ki=47 722.5；0轴的PID控制参数为kd=0.009 2，kp=58.384，ki=190 890.

3重复控制器的设计

根据内模原理可知，重复控制对死区影响以及其他周期性扰动具有很好的抑制作用，并且能够消除跟踪误差，使系统尽可能地达到无稳态误差形式[8—9]，重复控制系统结构框图如图4所示.

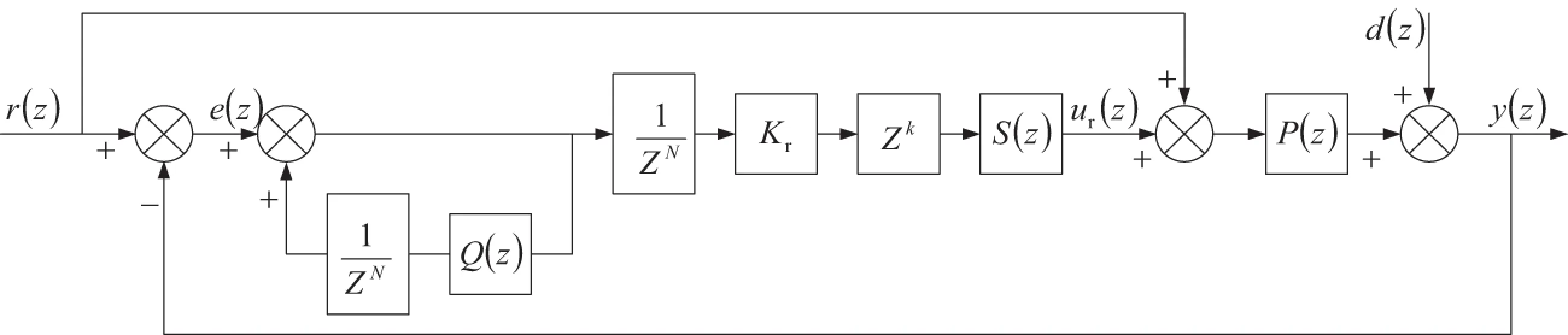
图4　重复控制系统结构框图

P(z)是控制对象，死区效应和其他扰动等效为扰动量d(z).1/ZN为周期延迟环节，与Q(z)组合为正反馈延迟环节.固有延迟环节的存在会延缓整个重复控制系统的作用时间，必须添加相位补偿环节Zk，使整个系统提前k拍进行校正.为了提高稳定性，减少稳态误差，加入重复控制增益Kr.S(z)为相位补偿环节，r(z)为输入参考电压，y(z)为输出电压，e(z)为误差值.Q(z)一般为一个低通滤波器[10]，也经常取小于1的常数[11]，为了设计方便，Q(z)取常数0.95.

消除被控对象的谐振峰值，采用陷波器，即零相移滤波器[12]，其传递函数为

(7)

单独的零相移滤波器不具备高频衰减能力，需要与二阶滤波器相互结合.d、q轴传递函数为

0轴传递函数为

N=200，要求通带内必须要有严格的线性相位，用z9进行补偿.重复控制增益Kr是为了保证系统在中频段和高频段的稳定性，Kr=0.9.

4仿真验证及分析

系统设计参数如下：直流母线电压为600 V，各相滤波电感为1.8 mH，各相滤波电容为30 μF，开关频率为10 kHz，输出电压频率为50 Hz.

1) 当三相四桥臂逆变器接不平衡负载时，令RA=30 Ω，RB=20 Ω，RC=10 Ω时，逆变器的电压、电流输出波形如图5和图6所示.从图6可以看出，由于负载的不同，其电流幅值相差比较大.但是经过闭环控制系统的调整，从图5可以看出，三相输出电压幅值基本一致，调节时间为0.04 s，即在0.04 s以后，整个系统进入基本稳定状态，三相电压的谐波畸变率分别为1.26%、1.31%、1.28%.可以看出，当外界负载因出现干扰发生变化时，电压仍能按照预期的目标输出，具有一定的抗干扰性.

2) 当三相四桥臂逆变器接非线性负载时，A相接二极管半波整流阻感负载，令RA=(40+j12) Ω，RB=20 Ω，RC=10 Ω时，逆变器的电压、电流输出波形如图7和图8所示.从图8可以看出，由于接的是非线性负载，电流幅值相差更大.但是经过闭环系统的控制，从图7可以看出，三相输出电压波形较为理想，三相电压的谐波畸变率分别为2.13%、1.43%、1.38%.谐波畸变率比接不平衡负载的情况要大一些，但是依然满足总谐波畸变率低于5%的要求.接不平衡负载的系统是最难实现控制的，也就是说，它的干扰是最大的，但是三相电压仍然以幅值基本相等的形式输出，证明该系统的鲁棒性较强.

图5　逆变器接不平衡负载时的三相电压波形

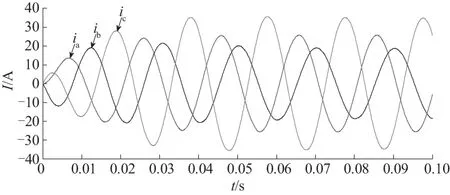
图6　逆变器接不平衡负载时的三相电流波形

图7　逆变器接非线性负载时的三相电压波形

图8　逆变器接非线性负载时的三相电流波形

图9为逆变器接非线性负载时的拓扑结构图，A相负载为单相半波可控整流电路，在仿真中代表非线性负载，其中电阻R=40 Ω，滤波电感L1=12 mH.通过以上两种情况可以看出，随着负载的变化，三相输出电流的幅值也进行相应变化，三相输出电压通过PID和重复控制的闭环控制，在经过短暂的调整之后，很快达到了预期的效果.

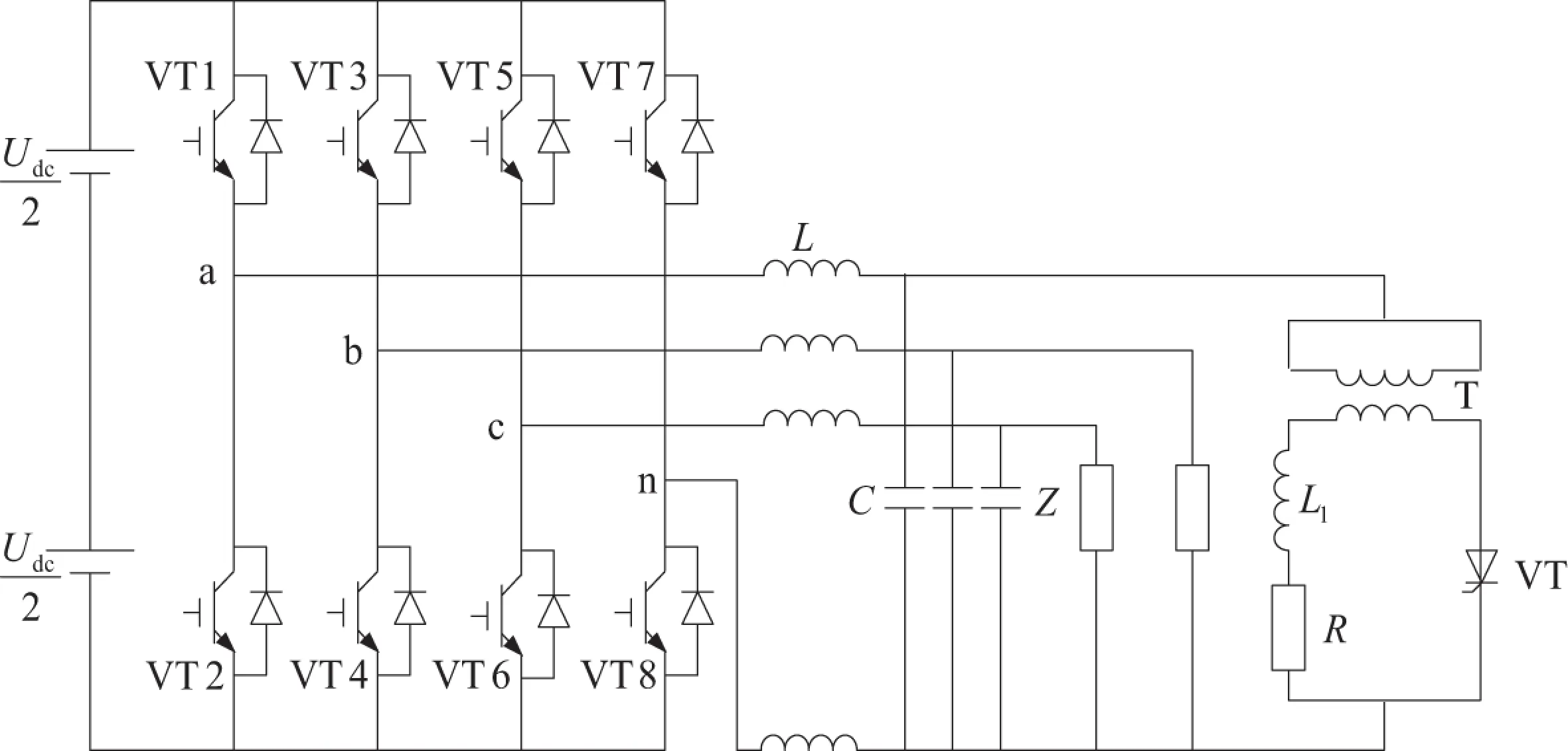
图9　逆变器接非线性负载时的拓扑结构

5结论

在三相四桥臂逆变器解耦为三个单相逆变器的基础上进行设计，将重复控制策略引入三相四桥臂逆变器，结合PID控制，构成双环控制，相辅相成，完成对整个系统的控制与实现，使其输出电压波形能够达到预期的效果.然后在三相不平衡负载和非线性负载的情况下进行仿真验证,仿真结果表明，逆变器输出的电能质量高，谐波含量相对较小，抗干扰能力较强.所设计的PID和重复控制双环控制策略，具有良好的有效性和可行性，整个系统具有很好的鲁棒性和动态特性.

参考文献：

[1]DXION J W,GARCIA J J,MORAN L．Control system for three-phase active power filter which simultaneously compensates power factor and unbalanced loads[J] ．IEEE transactions on industrial electronics，1995，42(6)：636—641．

[2]孙尧，粟梅，夏立勋，等．基于最优马尔可夫链的双极四脚矩阵变换器随机载波调制策略[J]．中国电机工程学报，2009，29(6)：8—14．

[3]王晓刚，谢运祥，帅定新，等．四桥臂逆变器的快速三维SVPWM算法[J]．华南理工大学学报(自然科学版)，2009，37(7)：94—99．

[4]罗国永，曹怀志，曾明高．三维电压空间矢量控制在三相四桥臂逆变器中的应用[J]．变流技术与电力牵引，2008(2)：21—23．

[5]张方华，丁勇，王慧贞，等．四桥臂三相逆变器的特定谐波消除控制[J]．中国电机工程学报，2007，27(7)：82—87．

[6]宦二勇，宋平岗，叶满园．基于三次谐波注入法的三相四桥臂逆变电源[J]．电工技术学报，2005，20(12)：43—46．

[7]王正仕，林金燕，陈辉明，等．不平衡非线性负载下分布式供电逆变器的控制[J]．电力系统自动化， 2008，32(1)：48—60．

[8]王斌，王凤岩．提高重复控制逆变电源的负载瞬态响应特性[J]．电源技术应用，2008，13(2)：6—9．

[9] 武健，何娜，徐殿国．重复控制在并联有源滤波器中的应用[J]．中国电机工程学报，2008，28(18)：66—72．

[10]TOMIZUKA M， KEMPF C．Design of discrete time repetitive controllers with applications to mechanical systems[C]//Proceedings of 11th IFAC Triennial World Congress.Tallinn,1990：243—248．

[11]TZOU Y Y,OU R S,JUNG S L，et al． High-performance programmable AC power source with low harmonic distortion using DSP-based repetitive control technique[J]．IEEE transactions on power electronics，1997，12(4)：715—725．

[12]郭卫农，陈坚．基于状态观测器的逆变器数字双环控制技术研究[J]．中国电机工程学报，2002，22(9)：64—68．

(责任编辑：孔薇)

The Research of Three-phase Four-leg Inverter Based on PID and Repetitive Control

LU Yan，GAO Fengyang，ZHANG Hongsheng

(SchoolofAutomationandElectricalEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China)

Abstract:A control strategy with PID and repetitive control was proposed, which was based on the three-phase four-leg inverter being decoupled into three single-phase inverters. Firstly, the switch cycle average method and the rotary coordinate transformation were used to establish average large signal model in rotating coordinate system. In addition, a simple PID controller could be designed based on this model. Then, a repetitive controller was applied to the whole system and the repetitive controller in outer loop reduced the distortion generated by periodic disturbance as well as enhanced steady state performance of the system. The results showed that output voltage characteristics and dynamic state performance of the inverter were excellent under unbalanced load and nonlinear load conditions.

Key words:three-phase four-leg inverter；single-phase inverter；PID control；repetitive control；decoupling control

收稿日期:2015-09-05

作者简介:路颜(1990—)，女，陕西渭南人，硕士研究生，主要从事电力电子与电力传动研究，E-mail:1114521660@qq.com; 通讯作者:高锋阳(1970—)，男，甘肃白银人，副教授，硕士，主要从事大功率电源与电力系统自动化控制研究，E-mail：13919878639@163.com.

中图分类号：TM464

文献标志码：A

文章编号：1671-6841(2016)01-0091-05

DOI:10.3969/j.issn.1671-6841.201509002

引用本文：路颜，高锋阳，张红生.基于PID和重复控制的三相四桥臂逆变器的研究[J].郑州大学学报(理学版)，2016，48(1)：91—95.