周期性纳米结构光散射分布的模拟仿真

赵　翔,高爱华,杨鹏飞,闫丽荣,王少刚

(西安工业大学 陕西省薄膜技术与光学检测重点实验室,西安 710021)



周期性纳米结构光散射分布的模拟仿真

赵翔,高爱华,杨鹏飞,闫丽荣,王少刚

(西安工业大学 陕西省薄膜技术与光学检测重点实验室,西安 710021)

摘要：为得到离子束刻蚀蓝宝石所形成的周期性条纹状纳米结构光散射分布特性,采用有限元法多物理场建模与分析,运用射频模块,结合麦克斯韦电磁波理论,引用弗洛奎特周期性边界和端口激发条件,对一维周期性条纹状纳米结构的光散射场进行数值分析.研究结果表明：一维周期性条纹状纳米结构TE与TM波光散射场分布呈周期性；随入射角不断增大,散射场分布沿纵轴呈凸状逐渐增强,入射角达到π/5时,TE波呈圆斑状周期分布,TM波呈斜条纹状周期性分布;经过后处理可得同一入射角下不同级反射系数之和为定值.

关键词：周期性纳米结构；电磁理论；散射场；反射系数

近年来,以蓝宝石为光学材料的研究备受人们关注.由于这种材料抗冲击、硬度高,通过离子束刻蚀技术在其表面形成周期性纳米结构后,可改善材料透过率和散射特性,因此在纳米电学、光电子学、光、电、磁功能器件方面有着巨大的应用前景[1].散射计算方法是光散射分布的研究依据,目前散射问题计算方法主要有T矩阵法、时域有限差分法、离散偶极子近似、矩量法和有限元法.文献[2]利用T矩阵法求解散射场值,其表达式简单,只与散射粒子的形状、大小、折射率及在坐标系中的位置有关,但更适合于颗粒状结构分析；文献[3]基于时域有限差分法对金属体散射、均匀介质体散射和非均匀介质体散射的电场进行计算,精确度较差；文献[4]运用离散偶极子近似主要对不规则形状的散射体的散射场的计算,只针对一些典型凝聚粒子的散射问题且精度不高；文献[5]采用的矩量法虽然精度最高、无需另设边界条件,但要面对繁难的积分方程；文献[6]主要讲述有限元法,其优点在于实施容易,精确度高于时域有限元差分法.

目前,周期性纳米结构主要有点状和条纹状两类.本文主要针对一维周期性条纹状纳米结构,采用有限元法,基于多物理场仿真软件,运用射频(Radio Frequency,RF)模块,以麦克斯韦电磁波理论为基础,引用弗洛奎特周期性边界和端口激发条件,对以蓝宝石为基底的理想一维周期性条纹状纳米结构光散射分布进行模拟仿真,并研究其光散射分布特性,运用此非接触式和非破坏性方法可避免传统分析的局限性和缺点.

1麦克斯韦方程的RF电磁理论

本文基于建模环境中RF(射频)模块对周期性条纹状纳米结构进行仿真.该模块用于电磁波领域内求解电磁问题,其中包括对散射电磁场的求解.从宏观角度看,电磁学分析问题是一个对边界条件已确定的麦克斯韦方程组的求解问题[7],由于仿真软件基于有限元法,而有限元法易于处理微分方程,所以对时变电磁场麦克斯韦方程可写成以下微分形式[8],表达式如下：

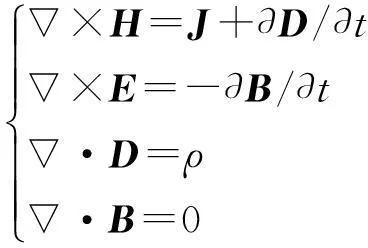
(1)

式中：E为电场强度;D为电通量密度(电位移矢量);H为磁场强度;B为磁感应强度；ρ为电荷密度;J为电流密度.方程式(1)中分别为适用于该结构的麦克斯韦安培定律、法拉第电磁感应定律、高斯定理电磁表达形式和电场表达形式,前两个方程揭示了电流、电场和磁场相互激励的性质；是旋度求解符号,主要表示电磁场中的空间位置变化；对时间t求导的过程表示时域的变化；∂D/∂t表示位移电流密度.

高频率的波,可以由麦克斯韦-安培定理和法拉第定律得到[9],表达式为

(2)

文中以离子束刻蚀蓝宝石形成的周期性条纹状纳米结构作为研究对象.蓝宝石是一种线性材料,各向同性,所以可结合物质方程,D=εE,J=σE,B=μH[7],变为

(3)

式中：σ为电导率；ε为介电常数；μ磁导率；分别针对电场和磁场对式(3)两边进行旋度求解得到

(4)

(5)

由于本文的电磁场求解域为频域,所以默认矢量场为空间变量,将场表示成时谐形式,表达式为

(6)

其中,eiw t和ejw t是用来代替时间变量的指数函数,w为角频率,这意味着通过一个因子iw、jw来替代对时间的求导,这样可以将方程表示为相位矢量函数,更有利于分析计算.通过麦克斯韦-安培定理和法拉第定律联立式将式(6)代入式(4)～(5)中,经过分析推导得到

(7)

(8)

式(8)描述了电场或磁场的运动规律。周期性条纹状纳米结构也可以通过将式(8)作为数学模型设定散射场参数,从而定义模型并对散射电场或磁场进行计算,最后得到散射场的分布状况,并研究其分布规律.

2周期性条纹状纳米结构模型

文中研究一束平面电磁波入射周期性条纹状纳米结构表面的散射场分布.周期性条纹状纳米结构几何模型,如图1所示.

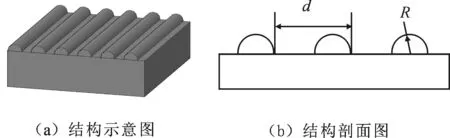
图1　周期性条纹状纳米结构

通过图1(a)可看出,周期性条纹状纳米结构与所熟知的光栅非常相似,图1(b)是结构剖面图,可看出结构的特征尺寸,但光栅的特征尺寸较大,一般都大于波长,而随着微加工技术的不断发展,光栅的特征尺寸越来越小,目前已经可以达到亚波长量级,即光栅的特征尺寸与波长近似或小于波长.文献[10]对金属线光栅的一维空间散射进行了模拟仿真得到散射场的分布图.本文的周期性纳米结构与金属线光栅近似,所以根据一维金属线光栅空间散射的研究过程可以对一维周期性纳米结构空间光散射场分布进行一定的指导,确保研究的正确性.

两平行折射与反射光的几何路径如图2所示.当两束光入射结构表面会发生相应的折射现象,如图2(a)所示.图2(a)中,光入射到两相邻单元路径发生衍射的条件是两光学路径之差等于真空波长的整数倍[10],其中m=0,±1,±2,…,真空波长是λ0,βm是m级衍射角,α是入射角,nα、nβ是上下空间折射率,关系式为

mλ0=d(sinβm-nαsinα)

(9)

当m=0时,符合折射定律sinβ0=(nα/nβ)sinα.由于正弦函数的值是在-1和+1之间变化,所以其最高衍射级满足-(nα+nβ)

(10)

图2　两平行折射与反射光的几何路径

若模型中涉及的波长比参数d足够小,将会呈现多级衍射级,为了减少衍射级利于图像分析,需要对波长进行一定的限制.

如图2(b)所示,光入射到相邻单元的两种路径发生衍射的条件为

mλ0=dnα(sinαm-sinα)

(11)

其中αm为m级衍射角.当衍射角m=0时,符合反射定律sinα0=sinα.这一模型不发生衍射的条件[10]为

(12)

文中nα=1(空气),nβ=1.765(蓝宝石基底),结构周期在100nm及以上(将周期定在400nm).经过以上分析计算,真空波长的值至少应大于553nm,根据文献资料及其他参数值情况,模型中波长定为λ0=589nm.

3软件仿真

运用软件中RF射频模块对一维周期性纳米结构散射分布进行仿真,实际使用port激发进行2D结构的仿真.这种仿真基于有限元法将连续的求解域离散为多个互不重叠的单元,将待求的未知量用每一个单元假设的近似函数进行组合并求解[11].仿真过程为理论分析、构建几何模型、参数设定、边界条件设定、网格划分、求解、后处理及总结[12].

3.1构建几何模型

通过图1(a)直观描述,在仿真中一维周期性结构对RF模块进行2D仿真,模型如图3所示(半径为80nm,周期为400nm).

图3　一维周期性结构2D仿真模型

3.2参数设定

参数设定分为全局参数、几何参数和材料参数.全局参数如图2(b)所示,周期性纳米结构的周期为d=400nm；波长为589nm；波频率表达式为c/λ0(真空波速与真空波长比值),值为5.0899E14(1/s)；入射角α设为00,这是由于其被指定为一个参数易在参数求解器中计算；折射角表达式为arcsin(nα*sinα/nβ).2D模型的几何参数为宽度10*d,高度3*d,半径d/5.材料设定方面,为计算方便将其分为空气、基底(蓝宝石)和凸起的周期性结构三个域.由于所研究对象定义为理想状态,材料在不同的方向所测得的性能数值完全相同亦称均质性,物理性质不随方向发生变化,所以各向同性.通过晶体材料光学参数查询可得相对磁导率0.000 9H·m-1,电导率0.099S·m-1,相对介电常数3.125 8,折射率1.765,折射率虚部0.055.

3.3边界条件设定

首先对各个域的频率电磁波方程进行设定,通过式(8)可知,空气与基底的频域波方程为εrE=0.在空气和基底这两个域的电位移场引入折射率εr=(n-ik)2,则σ=0和μr=1对于凸起的周期性结构的频域波方程为(εr-jσ/wε0)E=0.在这个域中电位移场引入介电损耗,那么εr=ε′-jε″.为使问题规模极小化,本模型将引入两个有效的边界条件：周期性边界条件和端口激发条件.

建立一个单元结构,引入弗洛奎特周期性边界来描述周期性.该条件下的解决方案是单元一边界等于相对应的另一边界乘以一个复数相位因子.边界之间的相移来自波矢量的垂直分量,且由于是连续的场,所以相位因子对折射、反射、入射波是相同的.周期性条件设定的方程[12]为

(13)

端口条件均用于指定的入射波,为了获得更完美的端口边界,图3的6个端口(最外边的六个边界)中每个端口的每个模式(m=0,m=-1,m=1)都应被表达.端口的类型是周期性,利用端口波激励给端口输入功率1,对输入量归一化.然后给每个周期的端口输入的振幅矢量以及入射角.每个周期的入射角被定义为

k×n=ksinαz

(14)

式中:n为入射波的法向量；k为入射波的传播矢；k为波数；z为z方向的单位矢量.通过软件自动创建端口的衍射级,提供端口边界的折射率和最大频率(本模型使用单一频率).

3.4网格划分

划分网格是建立有限元模型的重要环节,为更好地反映数据的变化规律,需采用比较密集的网格.本模型选用特别细化的自由剖分三角形网格,最大单元尺寸为4.8×10-8m,最小为1.8×10-10m,最大单元生长率为1.2,曲率解析度为0.25,狭窄区域解析度为1.

3.5求解得到的图像

求解中频率为f0(参数定义中已设定),入射角参数扫描开始是0,停止是pi/2～pi/40,步长为pi/40.由于结性能取决于入射波极化,所以需考虑TE与TM波,结果如图4～5所示.分别选取6个典型入射角0°,π/5,π/4,3π/10,2π/5和约π/2,并对其散射电场进行求解.通过散射电场分布图可以看出,TE波与TM波分布有所不同,入射角接近π/5,TE波沿横轴呈圆斑状周期分布,TM波沿横轴呈斜条纹状周期分布,但是入射角接近00或π/2,两波散射场分布都是沿纵轴呈凸状逐渐增强.

3.6仿真结果后处理

仿真结果后处理如图6所示.图6中R0、R-1和R1分别是0,-1和1级的反射系数[9].由图6可以看出,随着入射角度的不断增加,TE与TM波的R0反射系数有较为明显的变化；R-1反射系数在入射角小于30°时变化不明显,但30°之后有明显变化；R1反射系数在整个入射角不断增加的过程中几乎没有显著变化；且同一入射角下不同级反射系数之和为定值,近似为1.

图4　入射角分别为0°,π/5,π/4,3π/10,2π/5和约π/2的TE波电场分布

图5　入射角分别为0°,π/5,π/4,3π/10,2π/5和约π/2的TM波电场分布

图6　反射系数

4结 论

1) 当入射角接近π/5,散射场TE波沿横轴呈圆斑状周期分布,TM波沿横轴呈斜条纹状周期分布；当入射角接近0° 或π/2,TE波与TM波的散射场分布都是沿纵轴呈凸状逐渐增强.

2) 随着入射角的不断增加,TE与TM波反射系数发生一定的变化.当入射角较小、几乎垂直入射时,反射系数变化单一；入射角在20°～40° 范围内,反射系数变化相对比较复杂；当入射角达到π/5 时,R0凸起,此时镜面反射增强,说明π/5角入射该结构时,介电损耗相对较小；随入射角的不断增大,TE、TM波R0反射系数变化趋势相反,R1反射系数的变化比较平稳,R-1反射系数的变化趋势相似；同一入射角下不同级反射系数之和始终为定值.实际过程中周期性条纹状纳米结构包含半圆形、三角形和矩形等,不同形状建立的几何模型输入的几何参数不同,散射分布也会存在一定差异,因此该结论适用于半圆形周期性条纹状纳米结构的研究.

3) 研究的结果可为实际中周期性条纹状纳米结构的缺陷检测提供理论依据与参考,可在此基础上改变为不同形状的一维周期性条纹状纳米结构,分析其空间光散射场分布,增加研究意义与价值.

参 考 文 献：

[1]刘卫国,许晓慧,陈智利.自组织纳米微结构的制备技术[J].西安工业大学学报,2010,30(5):409.

LIUWeiguo,XUXiaohui,CHENZhili.ThePreparationTechnologyofSelf-assembledNanostructure[J].JournalofXi’anTechnologicalUniversity,2010,30(5):409.(inChinese)

[2]巩蕾,吴振森.基片表面微球体纳米级缺陷的光散射分析[J].中国激光,2011,38(1):1.

GONGLei,WUZhensen.SubstrateSurfaceMicro-sphereNano-sizedDefectsofLightScatteringAnalysis[J].ChinaLaser,2011,38(1):1.(inChinese)

[3]黄明红.FDTD方法在半空间散射问题中的应用[D].西安:西安电子科技大学,2011.

HUANGMinggong.TheapplicationofFDTDMethodintheHalfSpaceScatteringProblem[D].Xi’an:XidianUniversity,2011.(inChinese)

[4]王丽.DDA在粒子散射特性研究中的应用[D].西安:西安电子科技大学,2009.

WANGLi.TheApplicationofDDAinParticleScatteringCharacteristicsResearch[D].Xi’an:XidianUniversity,2009.(inChinese)

[5]BARZEGAR-PARIZIS,SHISHEGARAA.ElectromagneticWaveScatteringAnalysisfrom2-DPeriodicRoughSurfacesUsingComplexImagesTechnique[J].IEEETransactionsonGeoscience&RemoteSensing,2015,53(2):862.

[6]徐荣昌,孙会朝.有限元仿真技术的发展及其应用[J].莱钢科技,2008(4):13.

XURongchang,SUNHuizhao.TheDevelopmentofFiniteElementSimulationTechnologyandItsApplication[J].LaigangScience&Technology,2008(4):13.(inChinese)

[7]谢处方,饶克谨.电磁场与电磁波[M].北京:高等教育出版社,2011.

XIEChufang,RAOKejin.ElectromagneticFieldandElectro-magneticWave[M].Beijing:HigherEducationPress,2011.(inChinese)

[8]韩军,刘钧.工程光学[M].西安:西安电子科技大学出版社,2007.

HANJun,LIUJun.EngineeringOptical[M].Xi’an:XidianUniversityPress,2007.(inChinese)

[9]BORNM,WOLFE.PrinciplesofOptics[M].Beijing:PublishingHouseofElectronics,2009.

[10]COMSOLCo.,Ltd..PlasmonicWireGrating[EB/OL].(2013-05-03)[2015-11-10].http://cn.comsol.com/model/download/198281/models.rf.plasmonic_wire_grating.pdf.

[11]ZIMMERMANWILLIAMBJ.COMSOLMultiphysics有限元法多物理场建模与分析[M].北京:人民交通出版社,2007.

ZIMMERMANWILLIAMBJ.FiniteElementModelingandAnalysisforMultiplePhysicalFieldsbyCOMSOLMultiphysics[M].Beijing:ChinaCommunicationsPress,2007.(inChinese)

[12]陈小燕.基于COMSOL软件的大地电磁正演模拟[D].西安:长安大学,2014.

CHENXiaoyan.COMSOLBasedForwardModelingforEarthElectromagnetic[D].Xi’an:Chang’anUniversity,2014.(inChinese)

(责任编辑、校对张立新)

Simulation of the Light Scattering Distribution of Dimensional Periodic Nanostructures

ZHAOXiang,GAOAihua,YANGPengfei,YANLirong,WANGShaogang

(Shaanxi Province Key Lab of Thin Films Technology and Optical Test,Xi’an Technological University,Xi’an 710021,China )

Abstract:To get light scattering distribution of the periodic striped nanostructure in sapphire etched by ion beam,the light scattering field of one-dimensional periodic striped nanostructure is numerical analyzed,adopting finite element modeling and analysis for physical fields,and using the radio frequency module,the theory of maxwell electromagnetic waves and floquet periodicity and port excitation conditions.The results show:The distribution of scattering field of transverse magnesic (TE) and transverse electric (TM) wave of one-dimensional periodic striped nanostructure is periodic.With the increase of incidence angle,the light scattering field distribution along the longitudinal axis is gradually strengthen in convex shape;While the incident angle reaches π/5,TE wave is periodic distribution in round porphyritic cycle and TM wave in inclined stripe shape.After post-processing ,in the same angle of incidence,the sum of reflection coefficients at different levels has the fixed value.

Key words:periodic nanostructures;electromagnetic theory;scattering field;reflection coefficient

DOI:10.16185/j.jxatu.edu.cn.2016.04.003

收稿日期：2015-11-10

基金资助：陕西省工业科技攻关项目(2015GY048);总装基金项目(9140A18020214BQ52001)

作者简介：赵翔(1991-),女,西安工业大学硕士研究生.通讯作者：高爱华(1967-),女,西安工业大学教授,主要研究方向为光电测试技术及信号处理.E-mail:freegah@126.com.

文献标志码:中图号：N34A

文章编号：1673-9965(2016)04-0270-07