地震薄层反射系数谱反演算法研究及应用

孙雷鸣， 曾维辉， 方中于

(中海油能源发展股份有限公司钻采工程研究院 地球物理研究所， 湛江 524057)

0 引言

目前，提高地震资料分辨率一直是人们讨论的热门话题，地球物理学家也一直在探索如何拓宽地震资料的频带宽度以获得更高的分辨率。众所周知，地震分辨率是从地震资料中提取信息的关键，根据Widess理论[1]，在地震上时间厚度小于八分之一波长的薄层是无法分辨的，如果存在噪音或者是随着子波在地下传播范围增大，这个结论将变为四分之一波长[2]。如果地震薄层是潜在的储层或者是重要的流动单元，受限于现有的地震分辨能力，薄层的识别及其厚度的计算将变得非常困难。

谱反演是一种采用频谱分解技术,来提高小于调谐厚度的薄层成像的处理技术。最初是由John P. Castagna等人[2]提出的，在其发表的论文中提出了反射系数序列奇偶分解可以提高分辨率的理论，给出了谱反演的目标函数，指出谱反演能够分辨薄层反射系数的位置、极性和大小；John P. Castagna等[2-8,11-14]利用频谱分解获得的局部频谱资料信息来进行薄层反射系数谱反演，指出该方法具有不需要任何先验模型，不需要任何反射系数的数学假设，不需要任何层位约束，也不需要任何测井资料强制约束等优点，可用来分辨低于调谐厚度的地震薄层；John P. Castagna等人提出的谱反演目标函数为非线性方程，同时求解反射系数位置及大小，存在多解性和不确定性，直接求解难度较大。作者将谱反演目标函数转化线性方程组[17]并求解，发现要想求得精确解，需要0到Niquist频率的所有频率成分，而地震资料往往是带限的，袁三一[10]在文献中也提到了这一观点。如何解决这个问题，作者对此进行了探讨。

1 谱反演基本原理

1.1 谱反演目标函数的建立

谱反演根据地震记录和地震子波的频谱信息，从地震记录中去除地震子波的影响，从而得到反射系数序列。根据函数奇偶分解理论[2]，对于任意反射系数r(t)，都可以将其分解成奇反射系数对ro(t)和偶反射系数对re(t)(图1)。

图1 反射系数奇偶分解示意图Fig．1 Odd Even Decomposition of refection coefficients

r(t)=ro(t)+re(t)

(1)

其中ro(t)=[r(t)-r(t)]/2；re(t)=[r(t)+r(t)]/2。

John P. Castagna[2-8]对奇反射系数对的模拟研究表明，当厚度逐渐减小时，振幅先是增大(调谐)然后减小；而对偶反射系数对，则正好相反，随着厚度减小振幅先减后增。因此在实际的大多数情况中反射系数都包含着这二个奇偶反射系数，而地震响应则与这二个反射系数对的大小有关。

假定水平叠加后的零炮检距自激自收地震记录可以用褶积模型来表示，即s(t)=w(t)*r(t)，在频率域可表示为

S(f)=W(f)×R(f)

(2)

其中 “*”表示褶积运算;“×”表示乘积运算;S(f)为地震信号频谱;W(f)为地震子波频谱;R(f)为反射系数频谱。

下面简要给出谱反演的目标函数的推导过程。图2为一个两个反射系数薄层模型，反射系数时间位置为t1和t2，大小分别为r1和r2，时间厚度为T，反射系数可表示为

r(t)=r1δ(t-t1)+r2δ(t-t1-T)

(3)

若将分析点设置于地层中点，则式(3)又可表示为

(4)

对式(4)进行傅里叶变换，并根据反射系数奇偶分解理论、脉冲函数δ(t)性质以及欧拉公式可得

R(re,ro,T,f)=2recos(πfT)+j2rosin(πfT)

(5)

同理，对于分析点位于时窗中点的多个地层模型，可推导频率域反射系数表达式如下

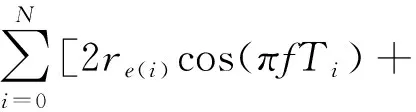
jro(i)sin(πfTi)]

(6)

式中N表示奇偶反射系数对的个数；Ti表示为第i层反射系数位置到分析点的2倍时间距离。

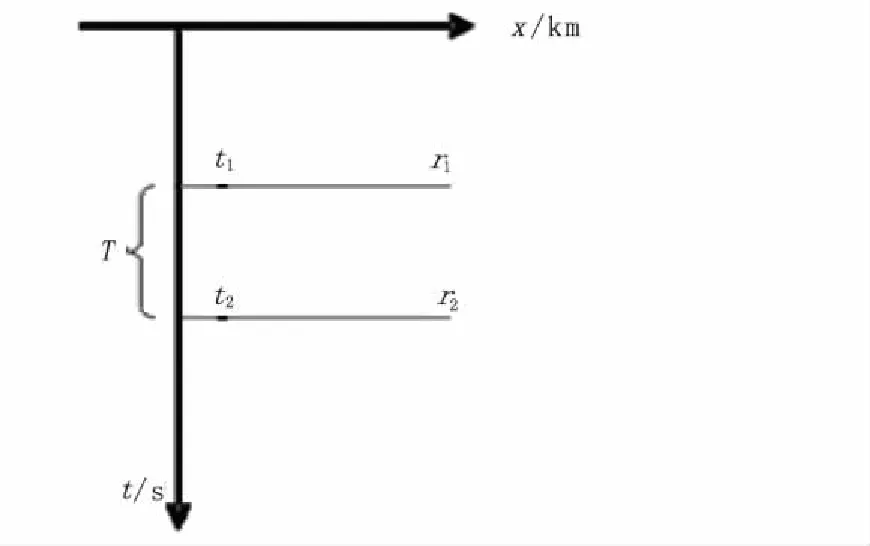
图2 两个反射系数地层模型Fig．2 Two-layer reflectivity modle

由于分析点设置在时窗中点，因此需要对地震信号进行时移，假如时窗长度为L，则时移量Δω=L/2，则式(6)等价于(7)

(7)

(8)

式中 Re[…]和lm[…]分别表示频谱的实部和虚部；fi表示采样频率；α和β分别表示反射系数的偶反射系数对和奇反射系数对所占的比例；fL和fH分别表示为最低频率和最高频率。

1.2 谱反演目标函数线性化

从式(8)可以看出，需求解的未知向量包括re、ro、T，即反射系数的大小及其位置，且这些未知量之间相互影响，存在多解性和不确定性，精确求解非常依赖于算法的全局寻优性能[9,10]。如果将方程转化一个线性方程组，问题可能会变得相对简单。

假如在反射系数位置已知的情况下，即向量T已知，待求解未知量仅为re和ro，设α=β=1，根据式(6)和式(7)，可得到以下线性方程组，即

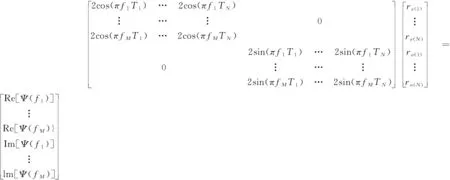
(9)

式中f1=fL；fM=fL；M为频率采样个数，一般为等间隔采样，采样率与傅氏变换时窗长度有关。

式(9)是在假设反射系数位置T=(T1,T2,…,TN)已知的情况下得到的结果，实际上，它是未知的。若假设地震道集每个采样点都看做是一个反射系数，其所在的时间位置便是一个已知值，并且假设频率分析时窗采样点个数L为偶数，采样率为Δt，则在式(9)中，N=L/2，Ti=(2i+1)Δt(i=1,2,…,N)，这样就避免了反射系数位置的求解，只需求解re和ro即可。

通过求解方程组(9)便可得到反射系数的奇反射系数和偶反射系数，然后对其进行重构便可得到反射系数的解。求解方法可采用SVD、共轭梯度法、LSCG[2]、最小二乘QR分解[16-17]等方法，本文采用最小二乘QR分解法对其进行求解。

2 线性谱反演存在的问题

由公式(2)可知，在不考虑噪音的情况下，反射系数频谱可以表示为

(10)

式中f∈[0,fN]；fN表示Nyquist频率。理论上基于(10)式的方程，旨在得到反射系数的反演，需要地震数据0到Nyquist频率的所有频率成分[10]。在假设每个时间采样点都存在一个反射系数值的情况下，所求未知量的个数远远超过真实反射系数的个数，这种要求显得更为苛刻。

图3是用30 Hz雷克子波合成地震记录在两不同频率范围内反演的结果，反射系数如图3(b)所示，从图3可以看出，该反射系数较为复杂，含有薄互层。合成地震记录采样间隔为 4 ms，图3(d)是在0到Nyquist频率(125 Hz)范围内反演的结果，从图3(d)可以出，反演效果非常理想，薄层得到了很好地反演；图3(f)是在 5 Hz 到 95 Hz 频率反演内反演的结果，从图3(f)可以看出，反演结果能量分散，真实反射系数位置周围存在 “抖动”，并且随着反演频带宽度的减小，反演效果会越来越差，能量越来越分散，分辨率也越来越低。

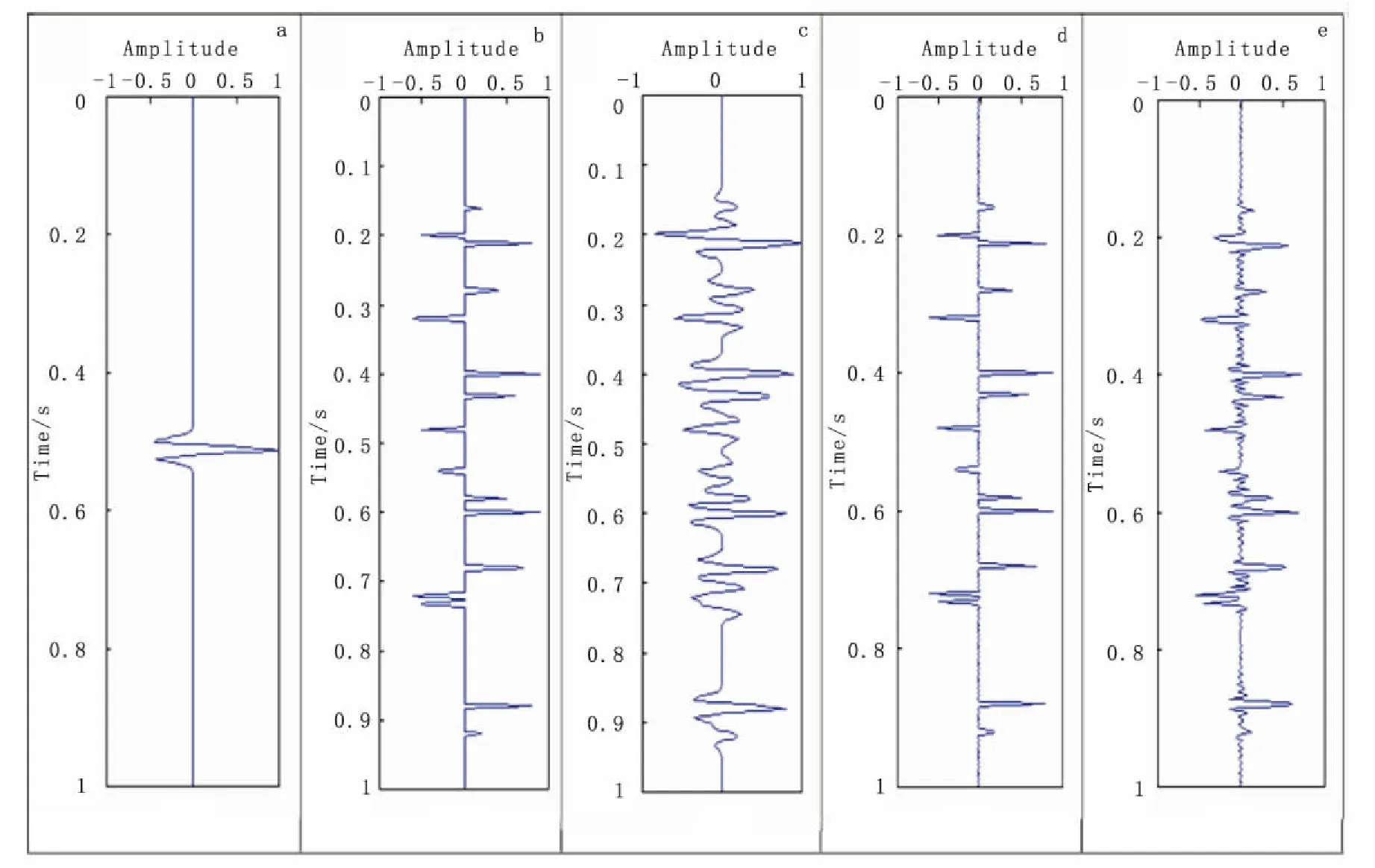
图3 合成地震记录不同频率范围反演的结果Fig．3 Inversion results of different spectrum of the same synthetic seismogram(a)Ricker子波；(b)反射系数;(c)合成地震记录；(d)[0,125Hz]反演结果；(e)[5,95 Hz]反演结果

在采样间隔为 4 ms 的情况下，Nyquist频率为 125 Hz，在f∈[0,125Hz]的情况下反演能取得好的效果，但在采样间隔为 2 ms 的情况下，Nyquist为 250 Hz，在f∈[0,250Hz]的情况下是否也能取得好的效果呢？采用图3的合成地震记录，但采样间隔为 2 ms。在频谱范围f∈[0,250Hz]反演得到的结果如图4(b)所示，反演结果并不理想，存在较大误差。将真实反射系数和反演得到的反射系数做傅里叶变换得到其频谱，如图4(d)和图4(c)所示，从图4可以看出，反射系数的高频区域没有得到正确反演。

事实上，地震子波是带限的，其高频成分的幅值接近于零值，在求解S(f)/W(f)时存在不确定性。基于式(10)的求解反射系数的方程组可以由式(11)来计算：[10]

(11)

其中相应振幅值接近于零的采样频率f，f∈[fhigh,fN]，rand表示一个随机复数。这便解释了采样间隔为 2 ms 时，基于所有频率成分没有取得好的反演结果的原因。

实际上所有的地震资料都是带限的，不可能利用所有的频率成分去反演反射系数，从而必须舍弃部分低频成分和高频成分。综上所述，对于线性谱反演，仅仅利用带限的地震资料去反演得不到精确解。 作者认为，要解决这个问题，必须假定反射系数是稀疏的，即地层介质波阻抗分界面处的反射系数为非零的，非地层介质波阻抗分界面的反射系数为零，而线性谱反演方法认为地震记录每个采样点都是一个反射界面，即反射系数是非稀疏的，因此需要对其进行稀疏约束。

3 线性谱反演约束方法

由于地震资料是带限的，不可能利用所有频率去进行反演，而线性谱反演假定反射系数在每个时间采样点均存在值，要想取得精确解就需要所有频率成分。在地震资料带限的情况下，如何提高线性谱反演的精度，作者对线性反演进行约束，成功地解决了这个问题。该方法分为两步，先在方程(9)加入Cauchy约束并反演，在反演结果中筛选若干反射系数(个数应不少真实反射系数的个数)，这些反射系数是稀疏的，时间位置已知，然后再利用式(9)对这些反射系数进行反演，反演时加入 L2 模约束。

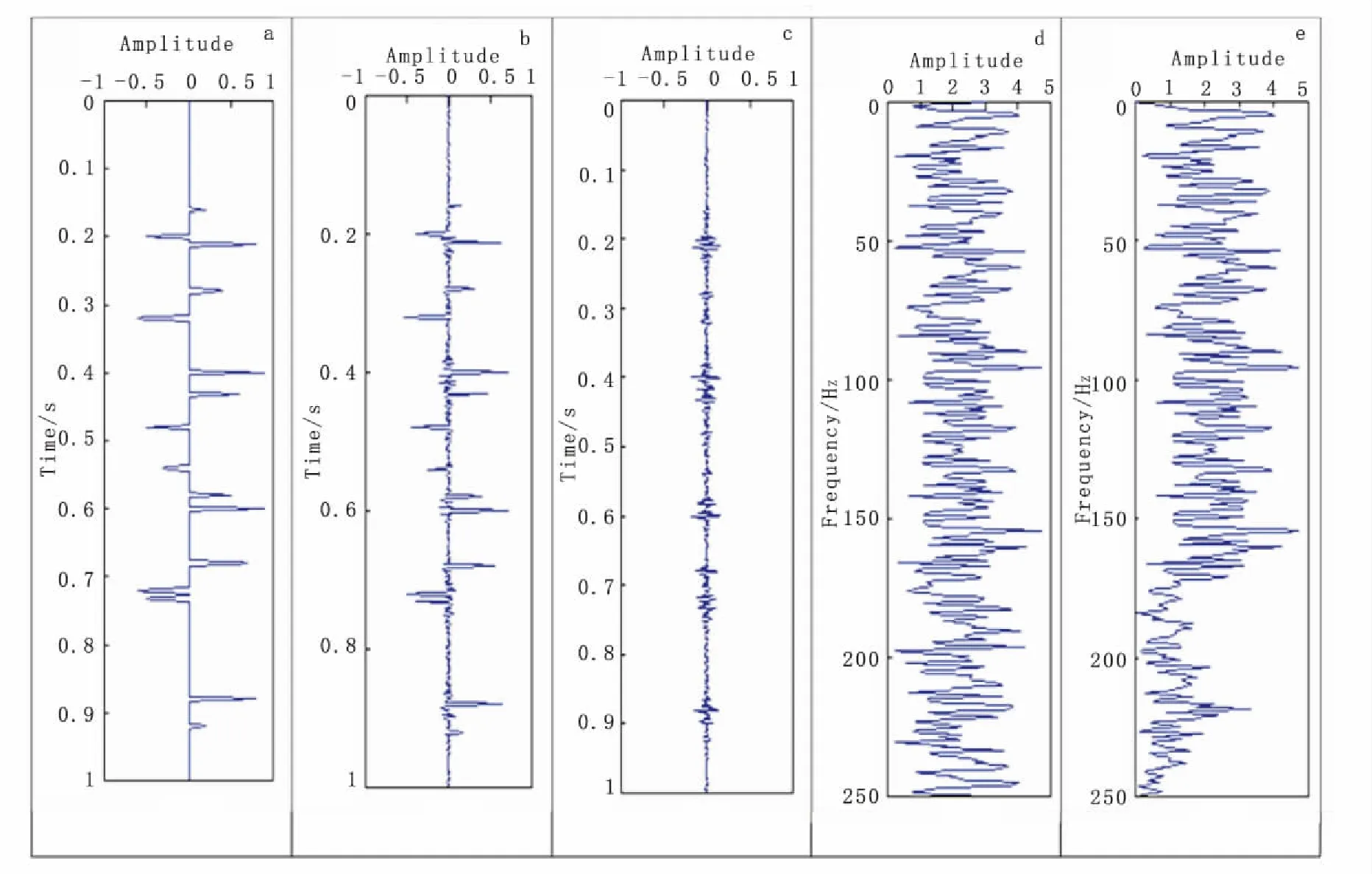
图4 合成地震记录反演的结果及频谱对比Fig．4 Inversion results of synthetic seismogram and spectrum comparison(a)反射系数；(b)反演结果；(c)反演误差；(d)真实反射系数频谱；(e)反演得到的频谱

Cauchy 约束即为稀疏约束，研究表明，Cauchy 约束准则在反射系数位置检测和抗噪等方面较为适用，反射系数的 Cauchy 分布可表示为[18-19]。

(12)

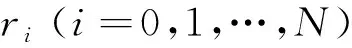
线性方程式(9)可简写为

Ar=b

(13)

式中A为方程式(9)的系数矩阵；r为奇偶反射系数序列，即r=(re(1),…,re(N),ro(1),…,ro(N))T，b=(Re[Ψ(f1)],…,Re[Ψ(fM)],lm[Ψ(f1)],…,lm[Ψ(fM)])T。方程式(13)引入 Cauchy 约束准则，则式(13)可表示为

(14)

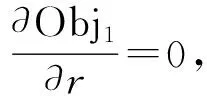
(ATA+Q)r=ATb

(15)

式中Q表示约束对角矩阵。

(16)

式(15)为非线性隐式格式，采用最小二乘 QR 分解法对其进行迭代求解。通过 Cauchy 约束求得的解并不是非常精确的，其值较真实值要偏小。为了提高反射系数反演的精度，从 Cauchy 约束反演得到的稀疏反射系数中筛选若干反射系数，这些反射系数的位置可以代表真实反射系数所在的位置，然后再对这些反射系数进行反演，并且在反演过程中加入 L2 模约束，保证算法的稳定性，收敛到真实解。此时反演的目标函数可表示为

Obj2=‖Ar-b‖2+μ‖r‖

(17)

式中μ表示阻尼因子。

4 理论模型试验分析

图5模型试验同样采用图3的反射系数及合成地震记录，时间采样间隔为 2 ms。仅对反演添加 Cauchy 约束，在频率范围[5,150 Hz]内得到的反演结果如图5(d)所示，与不加约束的反演结果(图5(b))进行对比可以看出，添加约束后反射系数使能量更加聚集到反射界面上，而不加约束的反演在真实反射系数周围存在明显的“抖动”，能量分散。尽管如此，加约束后反演得到的结果与真实反射系数相比还是存在较大的误差，如图 5(f) 所示，这是由于 Cauchy 约束本身对反射系数也进行压制而不可避免的。

图6是对 Cauchy 约束反演后筛选 80 个反射系数并再加 L2 模约束反演求得的结果，图6(b)是在频率范围[5,130 Hz]内反演得到的结果，从图6可以看出，得到的反射系数非常接近于真实反射系数，并且误差非常小；图6(d)是在频率范围[10,100 Hz]内反演求得的结果，从图6(d)可以看出，减少部分高频和低频成分，依然能求得好的反演结果，误差也非常小，但是相对于在频率范围[5,130 Hz]求得的反演结果误差要偏大，这说明参与反演的频率成分越多，反演效果就越精确。

5 实际资料应用

将本文提出的谱反演方法应用到实际叠后地震数据中，图7(左)是来自某一个工区的实际地震剖面，采样率是 1 ms，地震道长度为 8 000 ms，图7(右)是利用谱反演方法反演的反射系数剖面。反演子波是采用统计法计算得到的雷克子波，没有用到井数据约束，并且由于地震波在传播过程存在高频衰减现象，在不同时间段提取了不同的子波。从图7可以看出，反演得到的反射系数剖面与真实地层相对应，地震薄层也得到了很好地反演，如图7(右)方框区域，这些薄层用肉眼在地震剖面是无法识别的，同时反射系数剖面给出了比原始剖面更多的地层细节和断层细节，这对精细解释来说是非常有益的。

事实上谱反演不仅能保留中低频成分，还能较好地补偿高频成分。图8 是反演得到反射系数剖面(方框区)某一道与测井数据进行对比，利用声波测井曲线得到的真实反射系数与反演子波进行褶积，得到合成地震记录，地震道用蓝色标记，反演得到的反射系数与反演子波褶积得到的合成地震记录用红色标记，实际地震道用黑色标记。从图8可以看出，两者基本上是一致的，这说明反演结果真实反映了实际地层在地震已有的有限带宽内的信息。若将利用声波测井曲线得到的真实反射系数与一带宽较大的子波进行褶积，如图9所示，得到合成记录用蓝色标记，反演得到的反射系数与这个子波褶积的得到合成地震记录用红色标记。从图9可以看出，地震比较微弱的高频信息通过谱反演得到了很好补偿，并且与测井数据对应关系良好。

图5 合成地震记录[5,150 Hz]范围内加Cauchy约束前后的反演结果Fig．5 The comparison of inversion results before and after Cauchy restriction in synthetic seismogram's [5,150 Hz] frequency range (a)反射系数；(b)不加约束反演结果；(c)图(b)反演误差；(d)加约束反演结果；(e)图(d)反演误差

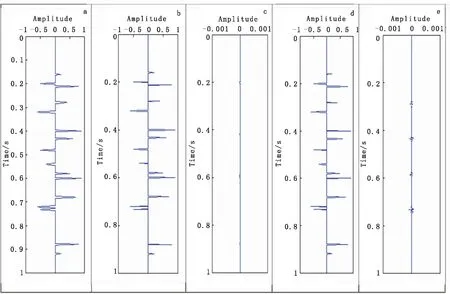
图6 不同频率范围的反演结果Fig．6 Inversion results of different frequency rang(a)反射系数；(b)[5,150 Hz]反演结果；(c)图(b)反演误差；(d)[10,110 Hz]反演结果；(e)图(d)反演误差

图7 原始地震剖面与和反演得到的反射系数对比Fig．7 The comparison of raw seismic section and inversed reflection coefficients

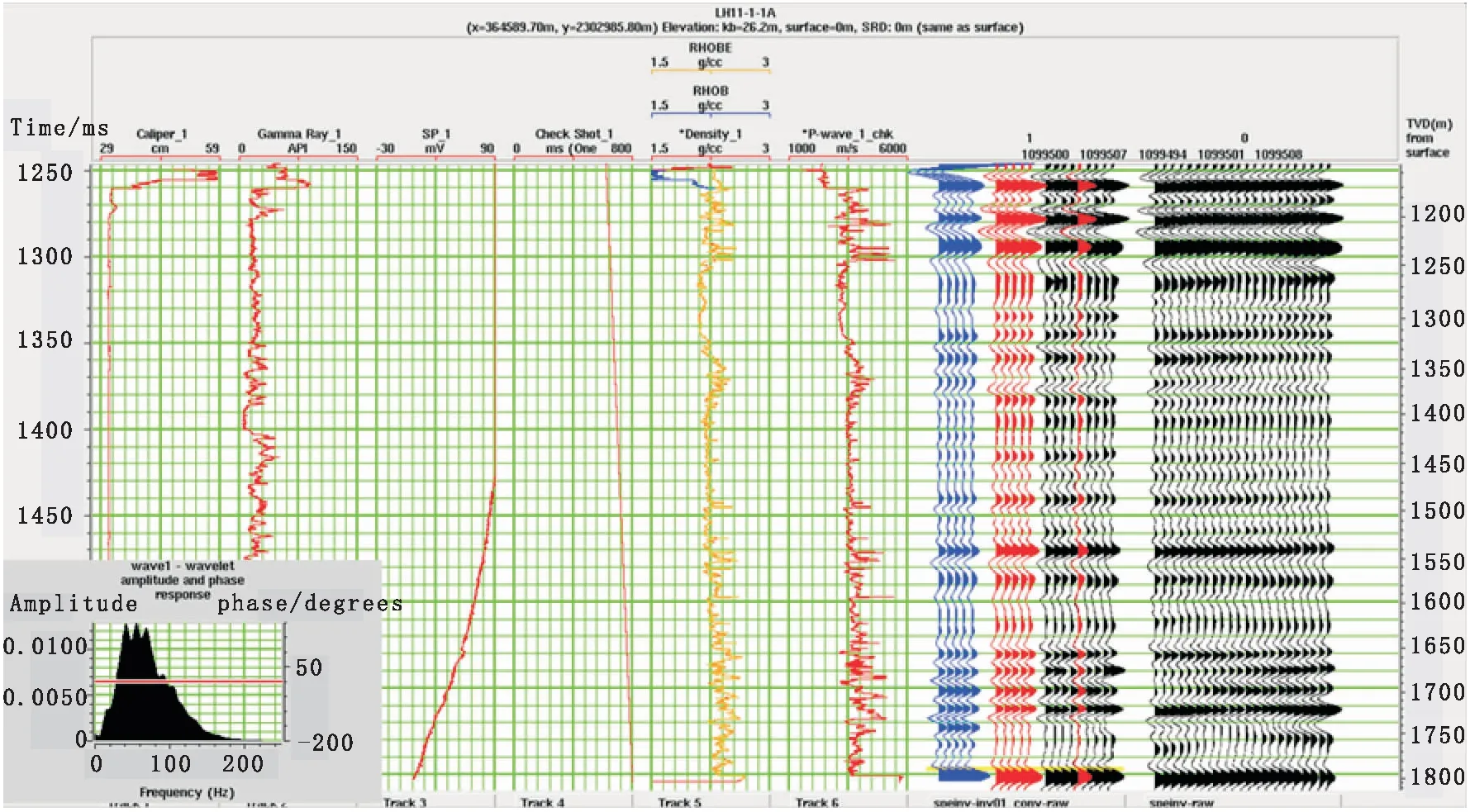
图8 反演得到的反射系数和实际子波的褶积与测井合成记录的对比Fig．8 The synthetic seismogram comparison of inversed reflectivity convolved with actual wavelet and well-log

图9 反射系数和宽频子波的褶积与测井合成记录的对比Fig．9 The synthetic seismogram comparison of inversed reflectivity convolved with broad spectrum wavelet and well-log

6 结论

谱反演是一种高分辨率反射系数成像技术，能分辨低于调谐厚度的薄层，并且不需要任何初始模型和先验信息约束。作者对谱反演线性方法进行了研究，揭示了假定所有时间采样点均存在反射系数的需要所有频率成分与地震资料带限之间的矛盾，直接求解不能求得精确解。针对此问题，作者认为只有在稀疏假设条件下的才能正确求解，通过在线性谱反演过程中添加Cauchy约束求得稀疏反射系数，然后挑选出这些稀疏反射系数，通过 L2 模约束再次求解，该方法在模型试算和实际资料应用过程中取得了好的效果。结果表明，本文提出的方法能有效分辨薄层，并且拓宽地震频带提高分辨率。该方法在实际应用仅考虑了地震子波的时变特征，若综合考虑子波的空变特征，反演效果会更佳。

参考文献：

[1] WIDESS M B. How thin is a thin bed? [J]. Geophysics, 1973, 38(6):1176-1180.

[2] PURYEAR C. I., CASTAGNA. J. P. Layer-thickness determination and stratigraphic interpretation using spectral inversion:Theory and application [J].Geophysics, 2008,73(2): 37- 48.

[3] CHOPRA S, CASTAGNA J. P., PORTNIAGUINE. O. Thin-bed reflectivity inversion [J].76th Annual International Meeting, SEG, Expanded Abstracts, 2006, 31(1): 2057-2061.

[4] CASTAGNA J. P. Spectral decomposition and high resolution reflectivity inversion [M]. Presented at the Oklahoma Section Meeting, SEG， 2004.

[5] CHOPRA S, CASTAGNA J P, XU Y, et al. Thin-bed reflectivity inversion and seismic interpretation [J].76th Annual International Meeting, SEG, Expanded Abstracts， 2007: 1923-1927.

[6] PORTNIAGUINE O, CASTAGNA J P. Spectral inversion: Lessons from modeling and Boonesville case study [J]. 75th Annual International Meeting, SEG, Expanded Abstracts, 2005:1638-1641.

[7] CHOPRA S, CASTAGNA J P, XU Y. Relative acoustic impedance application for thin-bed reflectivity inversion [J]. Expanded Abstracts of 79thAnnual Internat SEG Mtg, 2009:3554-3558.

[8] PORTNIAGUINE O, CASTAGNA J P. Inverse spectral decomposition [J], Expanded Abstracts of 74thAnnual Internat SEG Mtg, 2004,:1786-1789.

[9] YUAN S Y, WANG S X. A fast hybrid algorithm for spectral inversion [J]. Expanded Abstracts of 79thAnnual Internat SEG Mtg, 2009: 2447-2451.

[10] YUAN S Y, WANG SX, Xu Y C, et al. Ill-posed analysis for spectral inversion [J]. Expanded Abstracts of 79thAnnual Internat SEG Mtg, 2009:2442-2446.

[11] PURYEAR C I, CASTAGNA J P. An algorithm for calculation of bed thickness and reflection coefficients from amplitude spectrum [J]. Expanded Abstracts of 76th Annual International SEG Meeting, 2006: 1767-1770.

[12] CHOPRA S., CASTAGNA J. P., PORTNIAGUINE O. Seismic resolution and thin-bed reflectivity inversion[J]. CSEG Recorder, 2006:31(1):19-25.

[13] CASTANO K P, OJEDA G. Optimizing thin-layer mapping through Spectral Inversion: Performance of Genetic Algorithms and Simulated Annealing[J]. Expanded Abstracts of 80th Annual International SEG Meeting, 2010:1610-1614.

[14] CHOPRA S., CASTAGNA J. P., XU Y. Thin-bed reflectivity inversion and some applications [J]. First Break, 200905, 27(5): 17-24.

[15] KALLWEIT R S, WOOD L C. The limits of resolution of zero-phase wavelets [J]. Geophysics, 1982, 47(7):1035-1046.

[16] PAIGE C C, SAUNDERS M A .LSQR: an algorithm for sparse linear equations and sparse least squares [J]. ACM Transactions on Mathematical software, 1982,8(1):43-71.

[17] 柴新涛,李振春,韩文功. 基于LSQR算法的谱反演方法研究[J].石油物探, 2012, 51(1): 11-18.

[18] 邸海滨,郭玉倩,刘喜武. 基于稀疏约束贝叶斯估计的相对波阻抗反演[J].石油物探,2011,50(2):124-158.

[19] 曾锐，刘洪，陈世军.柯西约束盲反褶积技术在井间地震的应用[J].地球物理学进展，2004,19(1):166-172.

[20] 王宇，韩立国，周家雄.L1-L2范数联合约束稀释脉冲反演的应用[J].地球科学——中国地质大学学报，2009,34(5):836-840.