2015年镇江市中考数学压轴题赏析
2016-06-13袁宏观
袁宏观
数学压轴题是为考查考生综合运用知识的能力而设计的,集中体现知识的综合性和方法的综合性,多数为函数型综合题和几何型综合题. 中考压轴题大多是以坐标系为桥梁,运用数形结合思想,通过建立点与数即坐标之间的对应关系,一方面可用代数方法研究几何图形的性质,另一方面又可借助几何直观,得到某些代数问题的解答. 解题的关键是掌握几种常用的数学思想方法.
一是运用函数与方程思想. 以直线或抛物线知识为载体,列(解)方程或方程组求其解析式,研究其性质.
二是运用分类讨论的思想. 对问题的条件或结论的多变性进行探究.
三是运用转化的数学思想. 由已知向未知,由复杂向简单的转换. 中考压轴题是对考生综合能力的一个全面考查,所涉及的知识面广,思想方法也较全面. 因此,可把压轴题分离为相对独立而又单一的知识或方法组块去思考和探究.
原题呈现 如图1,二次函数y=ax2+bx+c(a≠0)的图像经过点(0,3),且当x=1时,y有最小值2.
(1) 求a,b,c的值;
(2) 设二次函数y=k(2x+2)-(ax2+bx+c)(k为实数),它的图像的顶点为D.
①当k=1时,求二次函数y=k(2x+2)-(ax2+bx+c)的图像与x轴的交点坐标;
②请在二次函数y=ax2+bx+c与y=k(2x+2)-(ax2+bx+c)的图像上各找出一个点M,N,不论k取何值,这两个点始终关于x轴对称,直接写出点M,N的坐标(点M在点N的上方);
③过点M的一次函数y=-x+t的图像与二次函数y=ax2+bx+c的图像交于另一点P,当k为何值时,点D在∠NMP的平分线上?
④当k取-2,-1,0,1,2时,通过计算,得到对应的抛物线y=k(2x+2)-(ax2+bx+c)的顶点分别为(-1,-6),(0,-5),(1,-2),(2,3),(3,10),请问:顶点的横、纵坐标是变量吗?纵坐标是如何随横坐标的变化而变化的?
【分析】本题是一道以二次函数为背景的题目,综合考查了待定系数法求函数解析式、二次函数的性质、函数图像上点的坐标特征、相似三角形的判定与性质以及一元二次方程的解法等知识.
(1)设函数解析式为顶点式,把(0,3)代入求得a,然后再把a的值代入化为一般式,即得a、b、c的值;
(2) ①当k=1时,可得函数解析式为y=
-x2+4x-1,令y=0时,求出x的值,可写出与x轴的交点坐标;②由于点M、N关于x轴对称,则点M和点N的纵坐标互为相反数,即ax2+bx+c+[k(2x+2)-(ax2+bx+c)]=0,解得x=
-1,代入函数解析式y=ax2+bx+c与y=k(2x+2)-(ax2+bx+c)中,即可求出点M,N的坐标;③易得一次函数解析式为y=-x+,可得此直线与x轴交点A(7,0),根据已知可得AE=8,MN=10,设MD交x轴于点B,作BC⊥MA于点C,利用三角形相似或锐角三角函数的定义列出等式,求得BC=3,将点B的坐标代入MB的解析式,即可求出k的值;④通过观察顶点坐标的变化可得:当顶点的横坐标大于-1时,顶点的纵坐标随横坐标的增大而增大,当顶点的横坐标小于-1时,顶点的纵坐标随横坐标的增大而减小.
②∵点M、N关于x轴对称,则点M和点N的纵坐标互为相反数,即ax2+bx+c+[k(2x+2)-(ax2+bx+c)]=0,2k(x+1)=0,不论k取何值方程都有解,∴x=-1,y=ax2+bx+c=x2-2x+3=1+2+3=6,点M的坐标为(-1,6),∴点N的坐标为(-1,-6).
∵MN⊥x轴,
∴E点的横坐标为-1,∴AE=8.
又∵ME=6,∴MA=10.
如图2,设MD交AE于点B,作BC⊥AM于点C.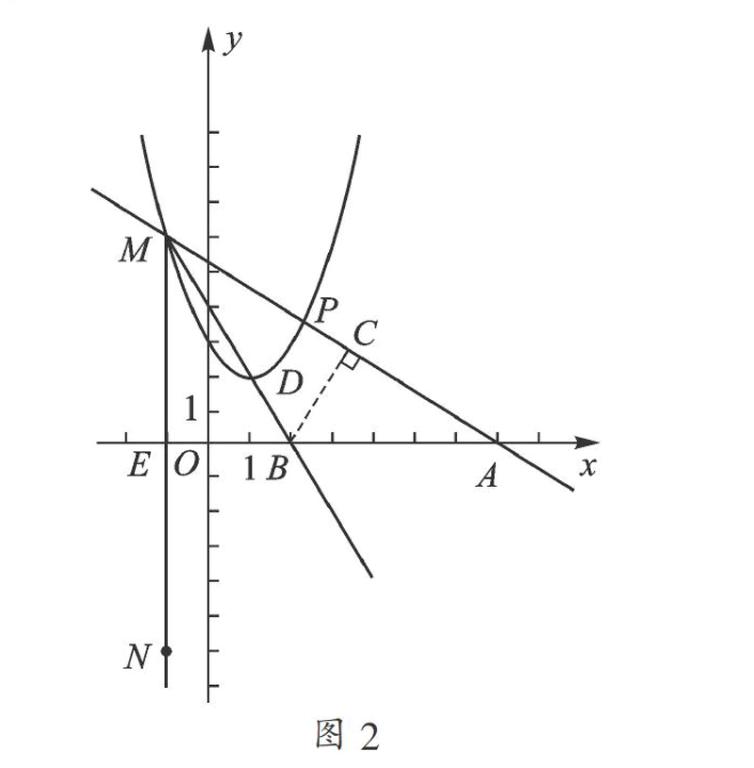
④是. 当顶点的横坐标大于-1时,顶点的纵坐标随横坐标的增大而增大,当顶点的横坐标小于-1时,顶点的纵坐标随横坐标的增大而减小.
