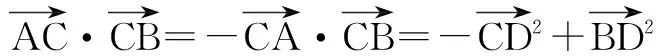巧用叠加法求条件最值

张云霄

(河南省濮阳市综合高中，457000)



巧用叠加法求条件最值

张云霄

(河南省濮阳市综合高中，457000)

在利用基本不等式求最值时,有许多同学感到力不从心,特别是对其中的“正”、“定”、“等”三个条件中的“等”总感觉防不胜防,一不留神就出现错解．下面举例介绍一种能有效防范三个条件中“等”的方法——叠加法．

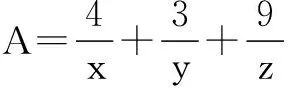
2A=A+A

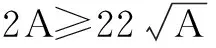
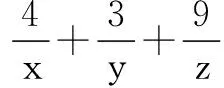
评注此类题目,同学们易出现如下错解:

≥4+6+12=22.

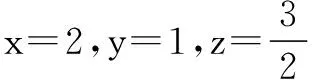
在上述解答中,通过叠加的方法促成等号成立的条件,防止了上述错误的发生．

利用类似方法,可以得到一般性结论:

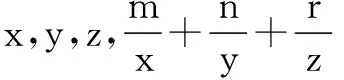
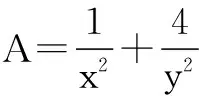
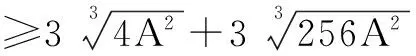
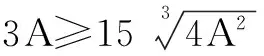
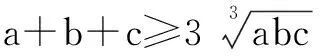
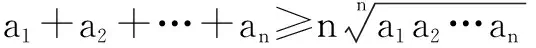
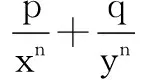
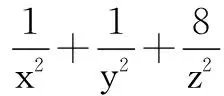
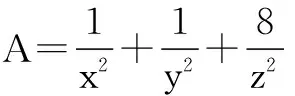
3A=A+2A

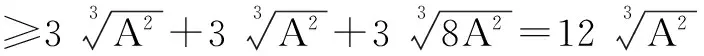
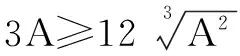
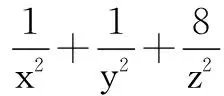
评注我们还可以解决如下更具有一般性的问题:

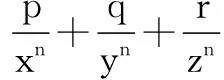
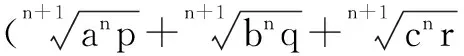
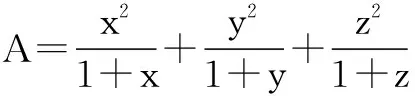
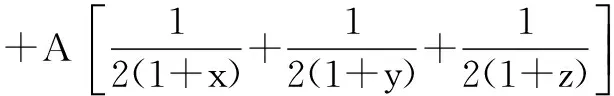
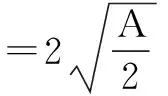
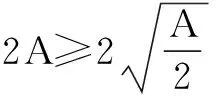
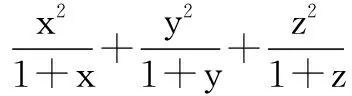
通过以上例子可以看出,用叠加法求最值,其本质是利用等式的基本性质,结合基本不等式求出最值．在叠加的过程中,促成基本不等式中等号成立的条件．该方法能有效解决用基本不等式求最值时,因等号成立条件为满足而取不到最值的常见问题,操作简便,易于推广,不失为一种好方法．

解如图2,取AB中点D,则