Revuz Measures,Energy Functionals and Capacities Under Girsanov Transform Induced by α-Excessive Function∗
2016-06-05RuiliSONG
Ruili SONG
1 Introduction and Preliminaries
In the theory of Markov processes,it is always interesting and important to explore various kinds of relationships between X and the transformed process of X under some kind of transform.Getoor and Ste ff ens[1]studied the relationships among the energy functional,the balayage operators and the capacities for a Markov process and the same objects for its qsubprocesses and u-transform;Ying[2]studied the homogeneous multiplicative functionals of Lévy processes and gave their characterizations;Ying[3]studied the additive and multiplicative functionals of a right Markov process systematically in the setting of weak duality and proved that any subprocess of a nearly symmetric Markov process was also nearly symmetric and gave a generalized Feynman-Kac formula;Ying[4]proved that the killing transform of Markov processes was equivalent to strong subordination of the respective Dirichlet forms and gave a characterization of so-called bivariate smooth measures;Ying[5]studied the htransform of symmetric Markov processes and corresponding Dirichlet spaces and discussed the drift transformation of Fukushima and Takeda’s type;Ying[6]studied the relationships of Revuz measures,several formulas on the energy functional and capacity between any process and its subprocesses.Chen et al.[7]investigated the most general Girsanov transformation leading to another symmetric Markov process.Fukushima et al.[8]extended the classical Douglas integral by using the approach of time change of Markov processes.Song and Ying[9]established a representation formula for transition density function of a certain type of rightprocesses under Girsanov transform and gave the in finitesimal generator of the transformed process.He and Ying[10]studied how energy functionals and Revuz measures change under time change of Markov processes and provided an intuitive and direct approach of the Lévy system and jumping measure of time changed process;Song[11]studied how Revuz measures,energy functional,capacity and Lévy system change under some Girsanov transform of Hunt processes.
Ying[5]considered a drift transformation which was in the setting of symmetric right process.In this paper,we consider a Girsanov transformation of a right Markov process which is formally like the drift transformation in[5].However,the right Markov process in our paper is not symmetric and the transformation is not the same.We will extend the excessive function in[11]to α-excessive function and generalize the results of[11].In the following,we will give the specific explanations.
We start from a right Markov process X=(Ω,F,Ft,θt,Px)t∈(0,+∞)on the state space(E,E)with transition semigroup(Pt){t>0}and resolvent(Uq){q≥0}.E is,at least,a separable Radon space and E is the Borel σ- field of E.A cemetery point Δ is adjoined to E as an isolated point of E and EΔ:=E∪{Δ},EΔ:= σ(E ∪{Δ})(the symbol‘:=’is always read as‘is defined to be’).Let ζ:=inf{t:Xt= Δ}be the lifetime of X.The filtration(F,Ft)is the augmented natural filtration of X.Denote by Excq(X)and Sq(X)(q≥0)the cones of q-excessive measures and q-excessive functions of X,respectively.As usual we write S:=S0,Exc:=Exc0.
For α >0,let h ∈ Sα(X)and 0 whereis a local martingale,is a continuous increasing additive functional.Refer to[12]for the theory of additive functionals. Let which is a martingale additive functional of X.Note that for t<ζ,we have Letbe the decomposition as continuous and purely discontinuous parts.Denote by Ltthe Doléan-Dade exponential martingale of.Then it admits a representation as the following: which is a martingale of X.Consequently,the formula uniquely determines a family of probability measure on(Ω,F∞).It is known that X is a right Markov process on E under these new measures(cf.[13,Section 62]).We will use(Y,F,Ft,Qx,x ∈ E)to denote the transformed process.Here Yt(ω)=Xt(ω)but we use Ytfor emphasis when working with Qx.By Itˆo’s formula,we have Let Qtand Vtbe the semigroup and resolvent of Y,respectively,that is,for any f∈E,we have The process Y is called the Girsanov transform of X by(Lt){t>0}or induced by α-excessive function h. In this article,we will get some potential objects under the transform,such as Revuz measures,energy functionals,capacities and Lévy systems. In this section,we will get the relationships of some potential objects between the process X and the transformed process Y which is defined in Section 1.In the following,we denote by Sq(Y)and Excq(Y)(q≥0)the cones of q-excessive measures and q-excessive functions of Y,respectively.Particularly,denote by S(Y)and Exc(Y)the cones of excessive measures and excessive functions of Y,respectively. Lemma 2.1For any q≥0,if u∈Sq(Y),then hu∈Sq+α(X).Particularly,if u∈S(Y),then hu∈Sα(X). ProofBy the definition of q-excessive function,we have By(1.1),we have Thus it follows that and Then also by the definition of q-excessive function,we have hu∈Sq(X). Lemma 2.2For any q ≥ 0,if μ ∈ Excq(Y),then∈ Excq+α(X).Particularly,if μ∈Exc(Y),then∈Excα(X). ProofWe assume that f∈pE(positive measurable function with respect to E)in the following.By the definition of q-excessive measure,we have μ∈Excq(Y)if and only if μe−qtQt≤ μ. Thus it follows that Thus we get the desired result. The above two lemmas give the relationships of excessive functions and excessive measures of X and Y. Revuz measures were first introduced for ordinary additive functionals in[14].Let m∈Exc(X)and A∈RAF(raw additive functional).Then the Revuz measure of A relative to m is defined by where ↑ (↓)means increasing(decreasing).Let Xαdenote the α-subprocess of X,that is,the semigroup of Xαis defined byWe have Let ρX, ρXαand ρYdenote the Revuz measures of X,Xαand Y,respectively. Theorem 2.1Let μ∈Exc(Y)and A be an increasing continuous additive functional which isfinite on[0,ζ[.Then Particularly,if∈Exc(X),then ProofIf At=(Xs)ds,where a is a bounded positive Borel function,then for any μ ∈ Exc(X),we have=a ·μ.Since μ ∈ Exc(Y),by Lemma 2.2,we have∈ Exc(Xα). Thus Then For a general A which is an increasing continuous additive functional,define a strictly increasing continuous additive functional H by Ht:=At+t∧ ζ,then By time-change,let Since AtHt,thendt.By Motoo’s theorem(cf.[13,(66.2)]),there is a bounded positive Borel functionsuch that=(Xs)ds for all t≥ 0 a.s..By the discussion in the first part of the proof,we have And by time-change(cf.[10]),we have Thus it follows that If∈Exc(X),by[15,(8.10)],we have then This theorem gives the relationship of Revuz measures between X and Y.In the proof,we use the method in[16].We see that time-change plays an important role in the above proof. The energy functional L(of X)is defined on Exc(X)×S(X)by Refer to[15]for the basic properties of energy functional L. Let LX,Lαand LYdenote the energy functional of X,Xαand Y,respectively. Before we get our results,we will explain our ideas as follows.Since h ∈ Excα(X)and Excα(X)=Exc(Xα),then h∈ Exc(Xα).Since 0 From(1.1),we see that the process Xα,hcan be seen as the killing process of Y by the decreasing multiplication functional M,where We will use the process Xα,has a bridge to get the relationships of energy functional and capacity between the process X and the process Y.We will get the relationship between Lα(LX)and LYin the following Theorem 2.2. Theorem 2.2Let μ ∈ Exc(Y),u ∈ S(Y),then Particularly,if∈Exc(X),hu∈S(X),then ProofBy Lemmas 2.1–2.2,we have Due to[1,(4.8)],we have The process Xα,hcan be seen as the M-subprocess of Y,where Due to Theorem 3.3 in[6],we have By(2.1)–(2.2),we have By Theorem 2.1,we have The Stieltjes logarithm of M is Due to[6,Corollary 2.8],we have Using(2.3)–(2.5),it follows that If∈Exc(X),hu∈S(X),since and then we have The Hunt’s balayage operationis defined on Excq(q>0).That is,for any terminal time T, For μ∈Exc(X), LetIf B ∈Eeand μ ∈Excq(q≥0),we shall writein place of For B∈Eeand q≥0,the q-capacity of B with m∈Exc(X)is defined by That is An exact terminal time T is called strict if T ◦ θT=0 a.s.In the case that T=TB,the hitting time of B∈Ee,T is strict if and only if XT∈Br,where Bris the set of regular points of B.The set B is called strict if TBis.Let ΓXand ΓYdenote the capacity of X and Y,respectively. Theorem 2.3Let B∈E and be strict,μ∈Exc(Y).Then Particularly,if,∈Exc(X)and∈S(X),then ProofSince μ∈Exc(Y),h∈S(Xα),then RBμ∈Exc(Y),∈S(Xα).By Lemma 2.2,we have,∈ Exc(Xα). By the definition of capacity,we have In the above reasoning,we use(2.1)to get the second equality and use[1,(5.4)(i)]to get the third equality. Since the process Xα,his the M-subprocess of Y,and by using[6,(4.11)],we have By(2.4)–(2.5),we get and By(2.8)–(2.11),we have the result(2.6). Particularly,if,∈Exc(X)and∈S(X),we have By(2.6)and(2.12)–(2.13),we have the result(2.7). A Lévy system for X is a pair(N,H),where N is a kernel on(E,Eu)(where Euis the σ-algebra of universally measurable subsets of E)with N(x,{x})=0 for any x∈ E and H is a continuous additive functional of X having bounded 1-potential,such that for any F ∈pEu×Euvanishing on the diagonal and any predictable process Z,we have where Refer to[13, §73]for the existence of Lévy systems.Now we state the relationship of Lévy system of X and Y. Theorem 3.1If(N,H)is a Lévy system of X,then(N?,H)is a Lévy system of Y,where ProofBy the definition of Lévy system,for any F ∈ pEu× Eu,we have The fifth equation is due to the continuity of H.Then also by the definition of Lévy system,we have that(N?,H)is a Lévy system of the process Y. AcknowledgementThe author is indebted to two anonymous referees for their constructive comments. [1]Getoor,R.K.and Steffens,J.,The energy functional,balayage and capacity,Ann.Inst.Henri Poincaré,23,1987,321–357. [2]Ying,J.,Multiplicative functional of Lévy processes,Stochastic Processes and Their Applications,58,1995,319–327. [3]Ying,J.,Bivariate Revuz measures and the Feynman-Kac formula,Ann.Inst.Henri Poincaré,32(2),1996,251–287. [4]Ying,J.,Killing and subordination,Proceedings of the American Mathematical Society,124(7),1996,2215–2222. [5]Ying,J.,Remarks on h-transform and drift,Chin.Ann.Math.Ser.B,19(4),1998,473–478. [6]Ying,J.,Revuz measures and related formulas on energy functional and capacity,Potential Analysis,8,1998,1–19. [7]Chen,Z.,Fitzsimmons,P.J.,Takeda,M.,et al.,Absolute continuity of symmetric Markov processes,Ann.Probab.Ser.A,32(3),2004,2067–2098. [8]Fukushima,M.,He,P.and Ying,J.,Time changes of symmetric diffusions and Feller measures,Ann.Probab.,32(4),2004,3138–3166. [9]Song,R.and Ying,J.,A formula for transition density function under Girsanov transform,Statistics and Probability Letters,77,2007,658–666. [10]He,P.and Ying,J.,Revuz measures under time change,Science in China Series A:Mathematics,51(3),2008,321–328. [11]Song,R.,Revuz measures under Girsanov transform,Chinese Journal of Applied Probability and Statistics,27(6),2011,569–578. [12]Blumenthal,R.M.and Getoor,R.K.,Markov Processes and Potential Theory,Academic Press,New York,1968. [13]Sharp,M.J.,General Theory of Markov Processes,Academic Press,New York,1988. [14]Revuz,D.,Mesures associées aux fonutionnelles additive de Markov 1,Trans.Amer.Math.Soc.,148,1970,501–531. [15]Getoor,R.K.,Excessive Measures,Birkhauser,Boston,1990. [16]Fitzsimmons,P.J.,Absolute continuity of symmetric diffusions,Ann.Proba.,25(1),1997,230–258.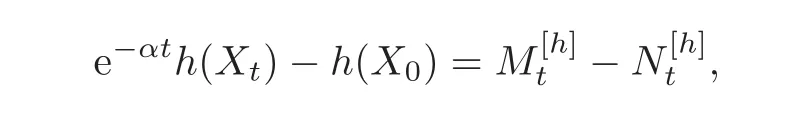
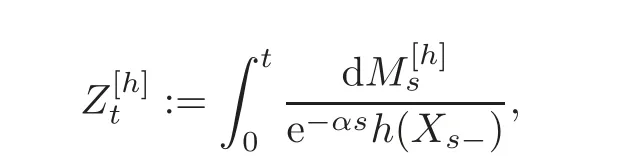
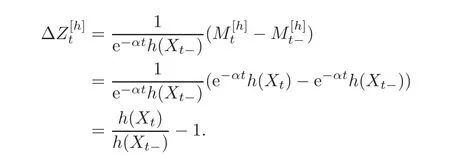
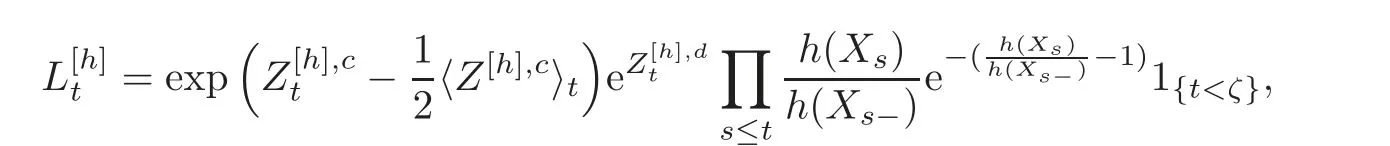

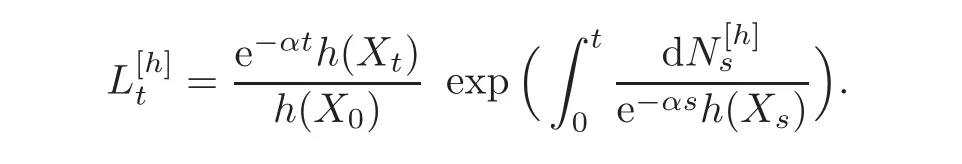
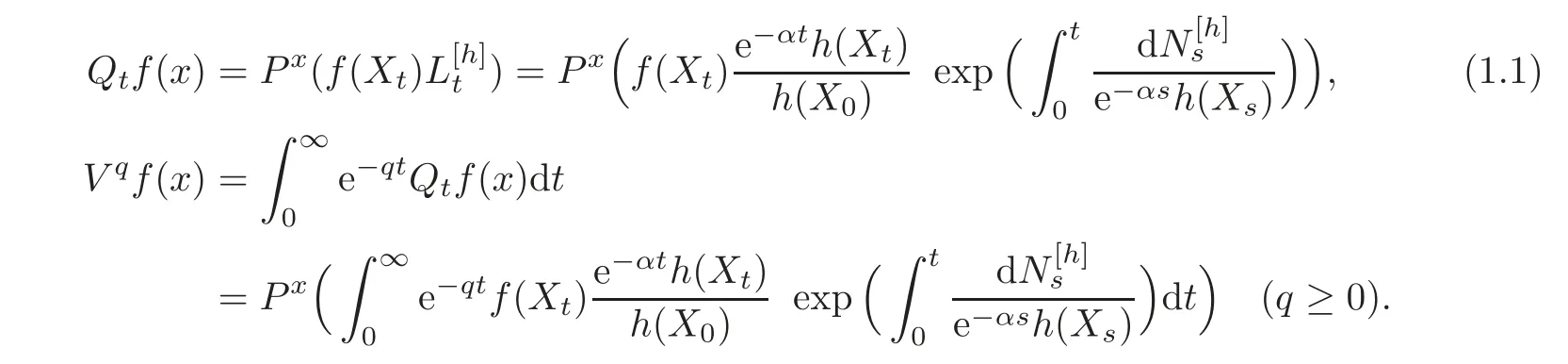
2 Revuz Measures,Energy Functionals,Capacities
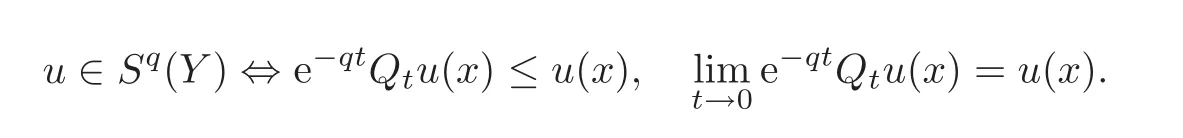

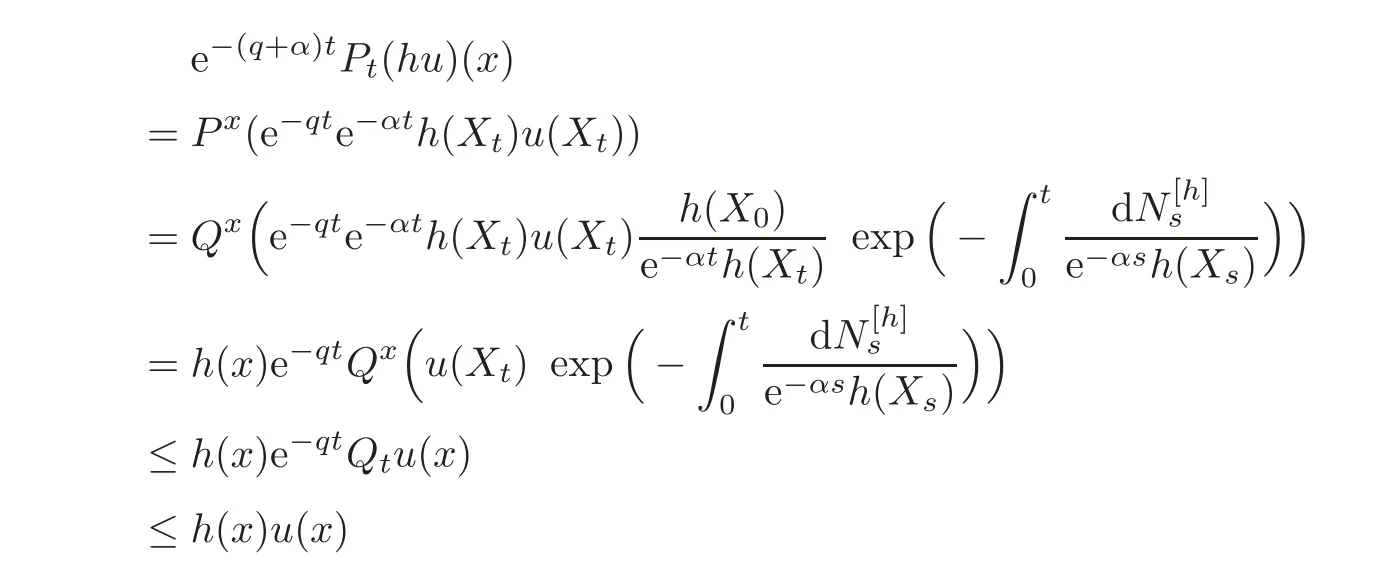
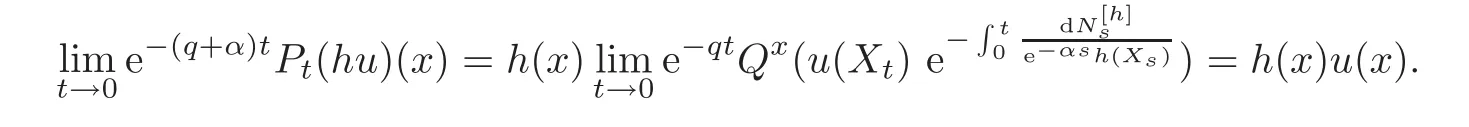
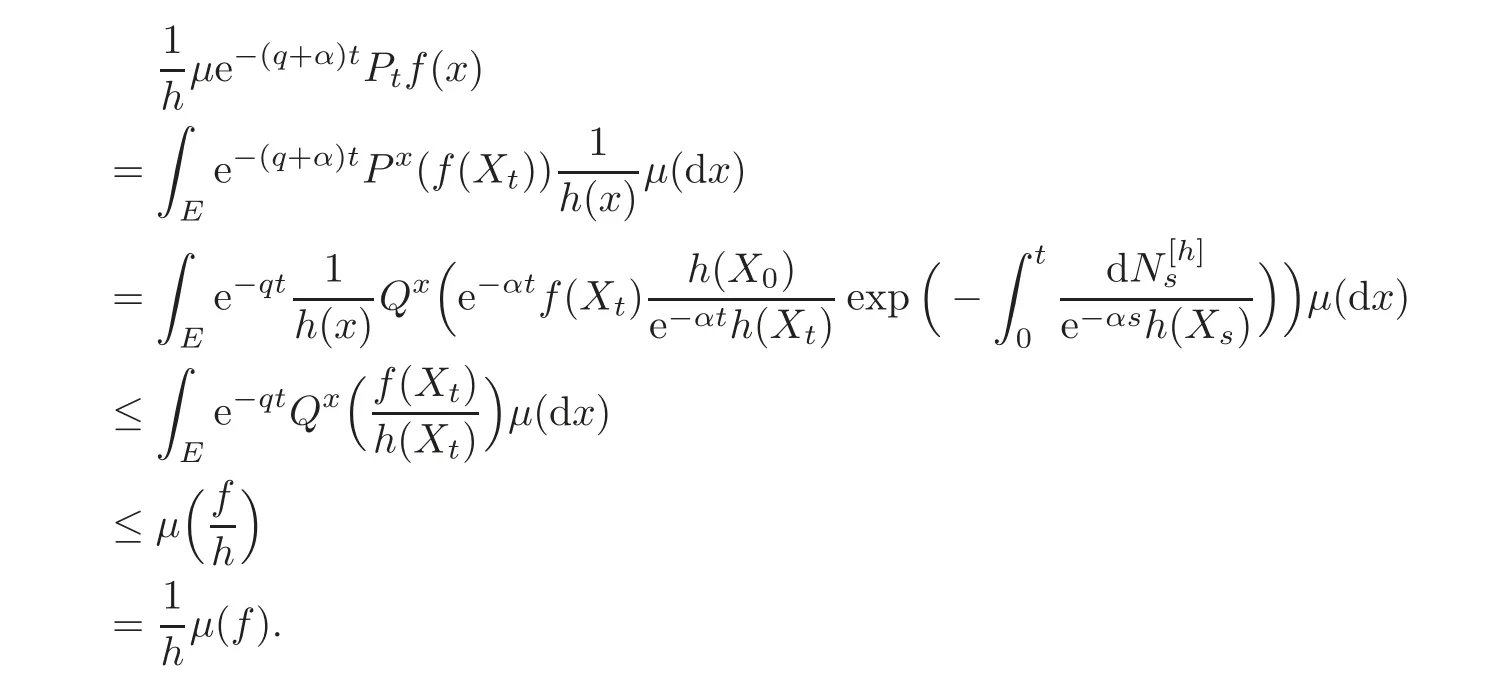
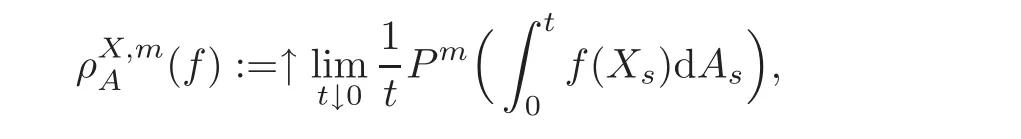
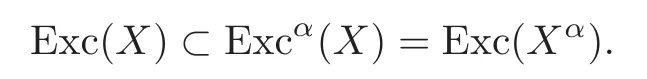

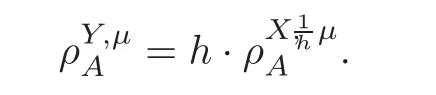
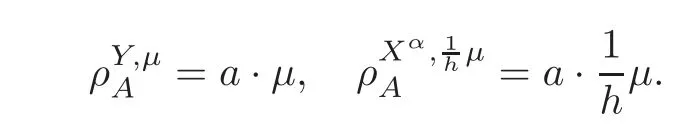
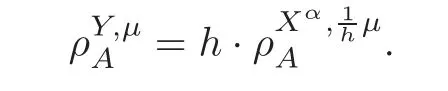

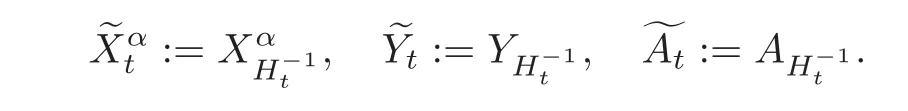
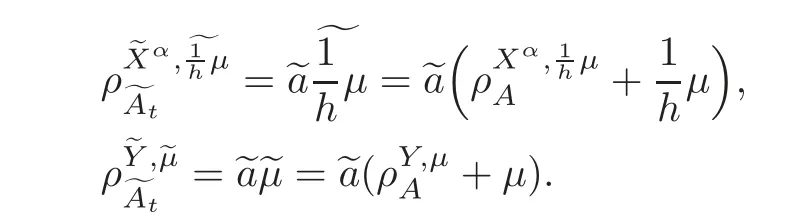
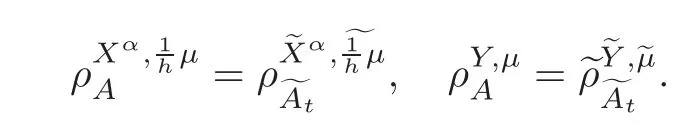

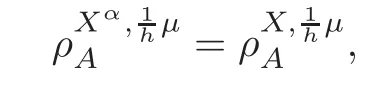
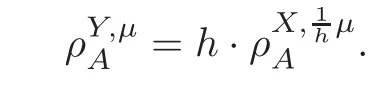
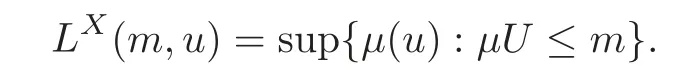
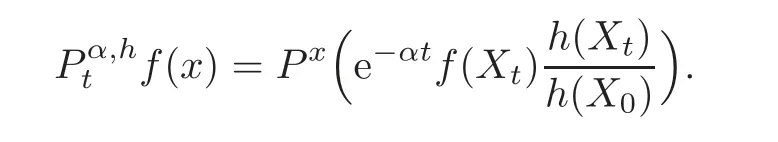
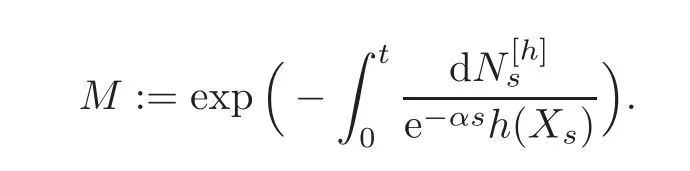

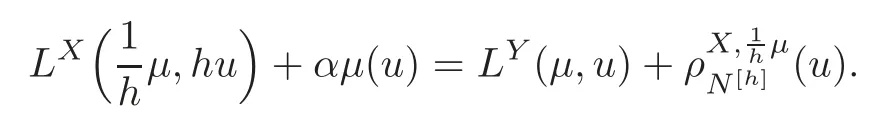
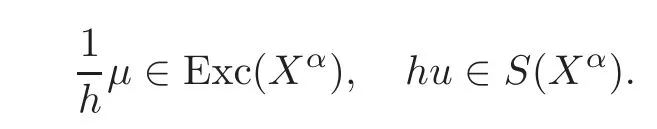
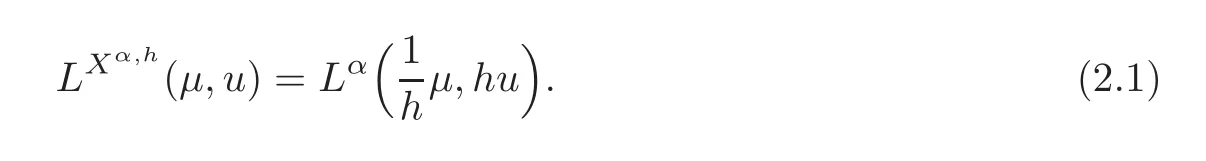
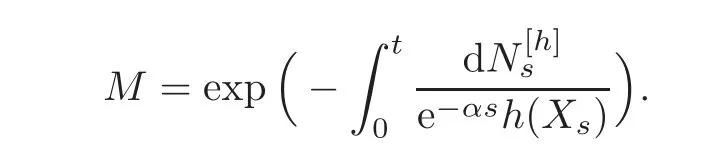
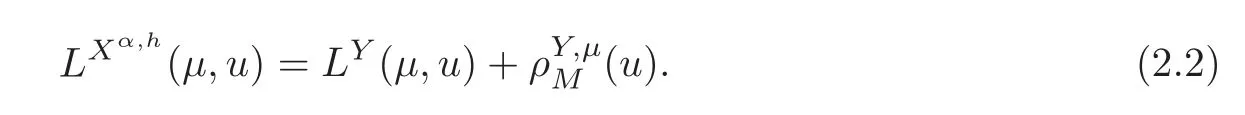
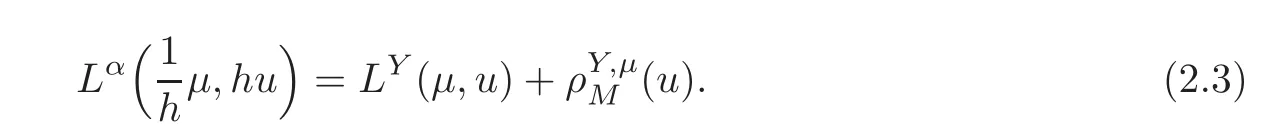

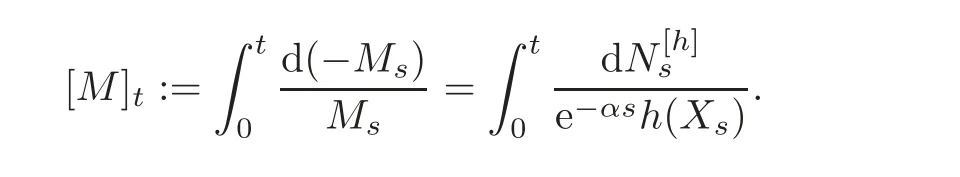
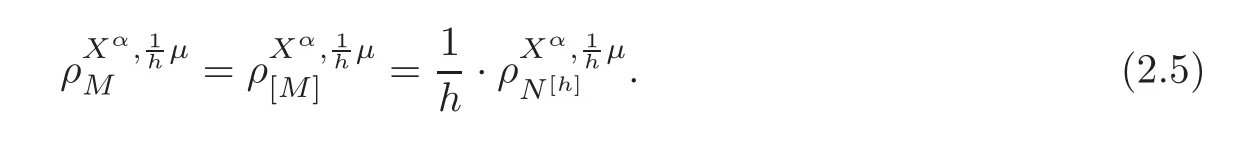
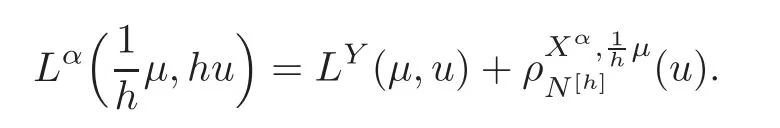
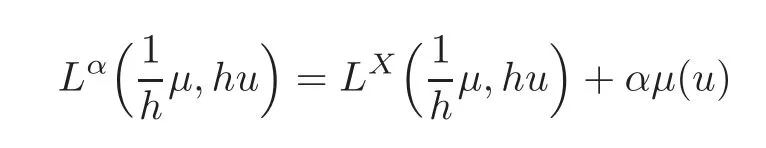
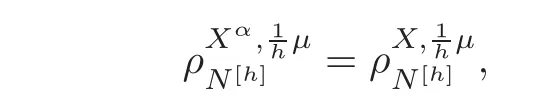
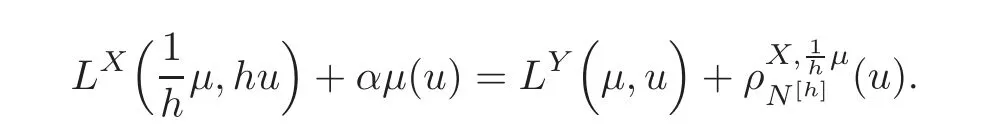
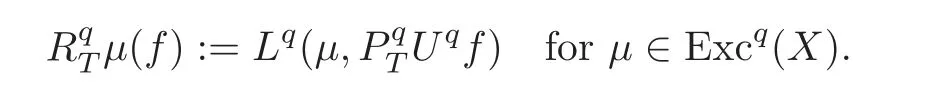

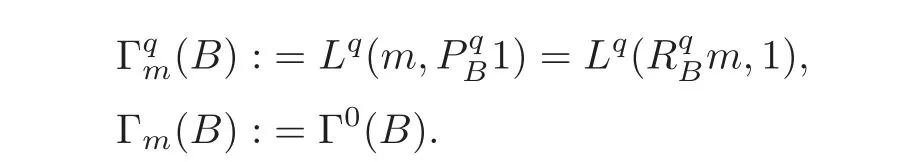
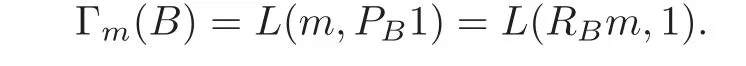

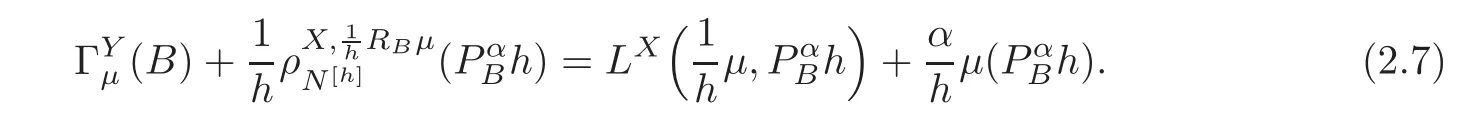
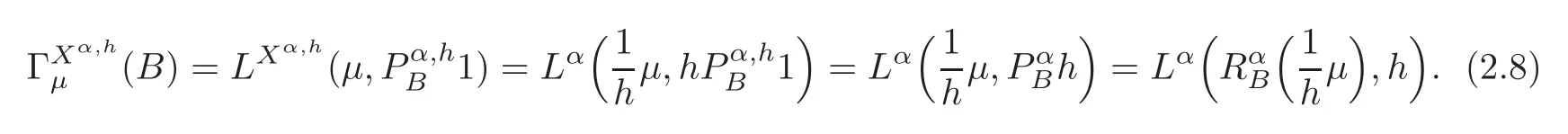
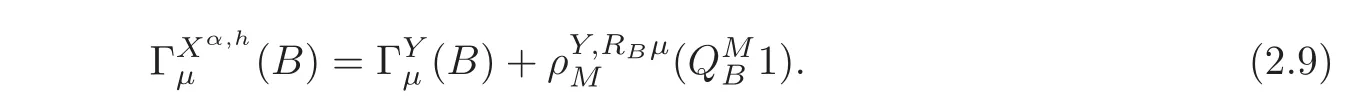


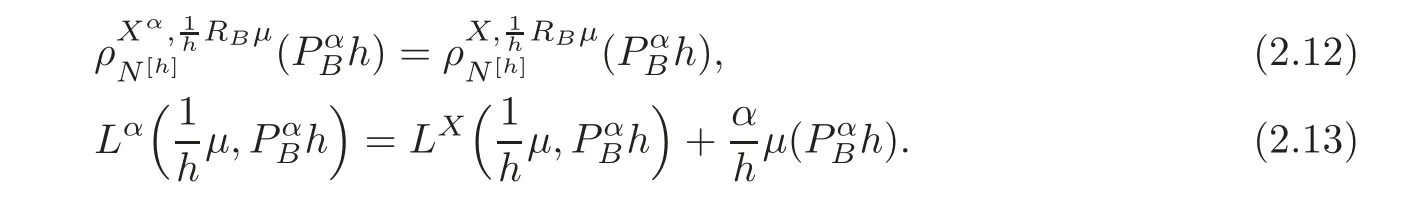
3 Lvy System
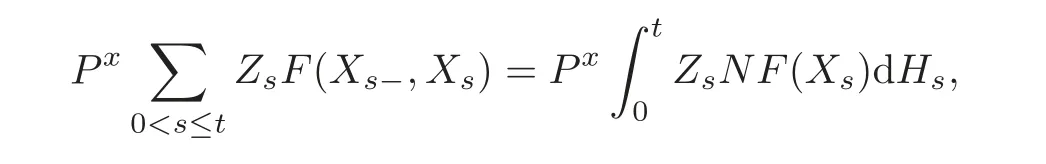
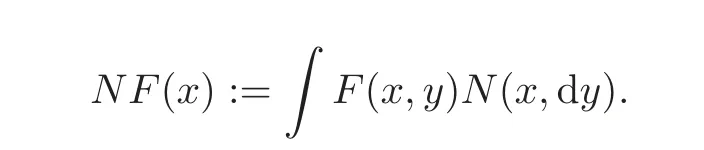
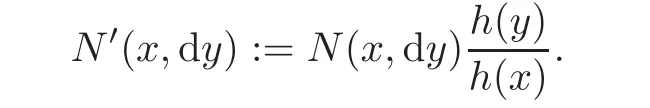

杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Exact Boundary Observability for a Kind of Second-Order Quasilinear Hyperbolic Systems∗
- Rational Structure of X(N)over Q and Explicit Galois Action on CM Points∗
- Homogenization of Elliptic Problems with Quadratic Growth and Nonhomogenous Robin Conditions in Perforated Domains
- Asymptotic Behavior of the Incompressible Navier-Stokes Fluid with Degree of Freedom in Porous Medium∗
- Modular Invariants and Singularity Indices of Hyperelliptic Fibrations
- New Quantum MDS Code from Constacyclic Codes∗
