Modular Invariants and Singularity Indices of Hyperelliptic Fibrations
2016-06-05XiaoleiLIU
Xiaolei LIU
1 Introduction
The modular invariants of a family of curves were introduced by Tan[10].They are the degrees of the pullback of the corresponding divisors by the moduli map.In the language of arithmetic algebraic geometry,a modular invariant is a certain height of arithmetic curves,for example,Faltings height is the modular invariant corresponding to Hodge class.Modular invariants can be used to describe the lower bound for effective Bogomolov conjecture which is about the finiteness of algebraic points of small height(see[15–16]).More recently,Tan found that the modular invariants are invariants of differential equations,which were expected by mathematicians in 19th century to study the qualitative properties of differential equations(see[11]).
Historically,the study of fibred surfaces is started by Kodaira[6],who gave a complete classification theory for elliptic fibrations.This combinatoric classification of elliptic fibers is used in the computation of the modular invariants.But such a classification is too complicate for the case when the genus g≥2.There are more than one hundred classes of singular fibers of genus 2(see[8–9]),and the number of classes of singular fibers increases quickly as the genus becomes bigger.Horikawa[5]classified the singular fibers of genus g=2 into 5 classes from a different point of view.Based on Horikawa’s work,Xiao[13–14]introduced the singularity indices(see definition 2.6)to classify singular fibers of hyperelliptic fibrations.Furthermore,he obtained the local-global formulas,and determined the fundamental group from his classification.
In what follows,we will prove that the two basic invariants,the modular invariants corresponding to boundary divisor classes and the singularity indices,coincide with each other for semistable fibrations.
Before starting this result,we explain our notations and assumptions.
A family of curves of genus g is a fibration f:S→C whose general fiber F is a smooth curve of genus g,where S is a complex smooth projective surface,and C is a smooth curve of genus b.The family is called semistable if all the singular fibers are semistable curves(recall that a semistable curve F is a reduced connected curve that has only nodes as singularities and every smooth rational component of F meets the other components at no less than 2 points).If all the smooth fibers are hyperelliptic,we say that the family is hyperelliptic.We always assume that f is relatively minimal,i.e.,there is no(−1)-curve in any singular fiber.
If r is a non-negative real number,we denote by[r]the integral part of r.Hence when m is a positive integer,m−2??is zero if m is even,or 1 otherwise.
For a fibration f:S→C,we have three fundamental relative invariants which are nonnegative,
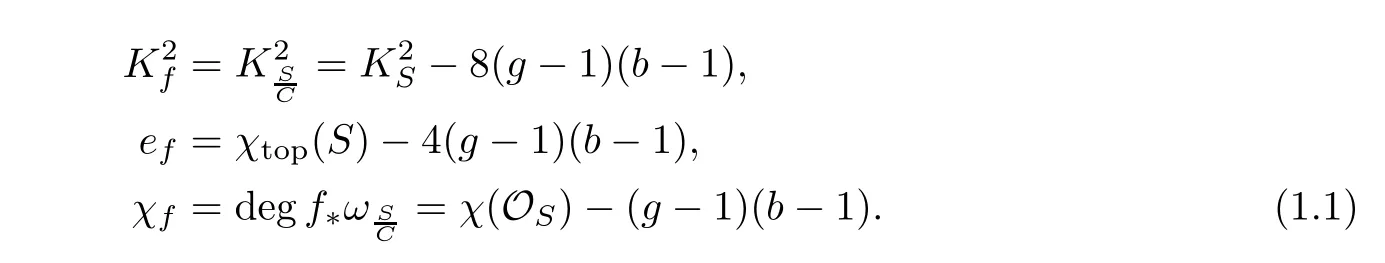
Let f be a locally non-trivial fibration,the slope of f is defined as λf=
For g≥2,the moduli map J:C→induced by f is a holomorphic map from C to the moduli spaceof semistable curves of genus g.For each Q-divisor class η of,we can define an invariant η(f)=degJ∗η which satisfies the base change property,i.e.,if?f:→is the pullback fibration of f under a base change π :→ C of degree d,then=d ·η(f)(see[10]).Consequently,for a non-semistable family f,we have η(f)=,whereis the semistable model of f corresponding to a base change of degree d.We call η(f)the modular invariant of f corresponding to η.
Let Δ0,···,be the boundary divisors of,and δi(f)be the modular invariant corresponding to the divisor class δi=[Δi]in⊗ Q,i=0,1,···,.Let λ ∈⊗ Q be the Hodge class,δ= δ0+ ···+,and κ =12λ − δ.For these classes,we have modular invariants λ(f), δ(f)and κ(f)of f.If f is semistable,then

We say that a singularity p in a semistable curve F is a node of type i if its partial normalization at p consists of two connected components of arithmetic genera i and g−i≥i,for i>0,and is connected for i=0.The node of the semistable curve corresponding to a general point of Δ0is α-type,i.e.,an ordinary double point of an irreducible curve,hence it is a node of type 0.For a general point in Δi,the corresponding node is of type i(i≥ 1)(see Figure 1).Denote by δi(F)the number of nodes of type i(i≥ 0)in F.
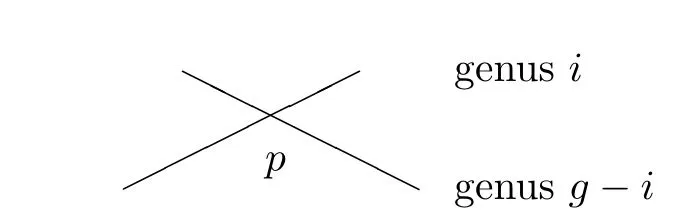
Figure 1 Node of typei(i≥1)
The general point in the intersection Δi1∩ ···∩ Δikof k distinct boundary divisors corresponds to a semistable curve with k nodes which are of types i1,···,ikrespectively.
Letbe the moduli space of semistable hyperelliptic curves,the restriction of Δ0onbreaks up into Ξ0,Ξ1,···.We denote by Θithe restriction of Δi(i ≥ 1)onSuppose that F is a semistable hyperelliptic curve with hyperelliptic involution σ,and p ∈ F is a node of type 0.If p= σ(p),then we set k=0;if pσ(p),and the partial normalization of F at p and σ(p)consists of two connected components of arithmetic genera k and g−k−1≥ k,then the node p(resp.nodal pair{p,σ(p)})is called a node(resp.nodal pair)of type(0,k).Then the nodal pair of the semistable curve corresponding to a general point of Ξkis of type(0,k)(see Figure 2).
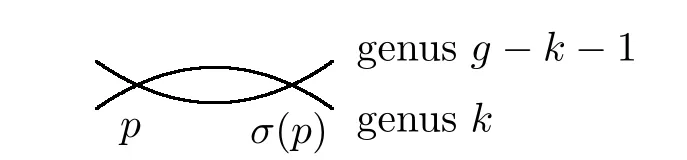
Figure 2 Nodes of type(0,k)(k≥0)
A semistable hyperelliptic curve is a double cover of a tree of rational curves branched over 2g+2 points(see[1,X.3]),which is induced by the involution map.Since the points p and σ(p)map to the same point in some P1,we treat them together as a nodal pair{p,σ(p)}.
Let

Denote by N2k+2(F)(resp.N2k+1(F))the set of all the nodal pairs{p,σ(p)}of type(0,k)(resp.nodes p of type k)(k>0).Then we define
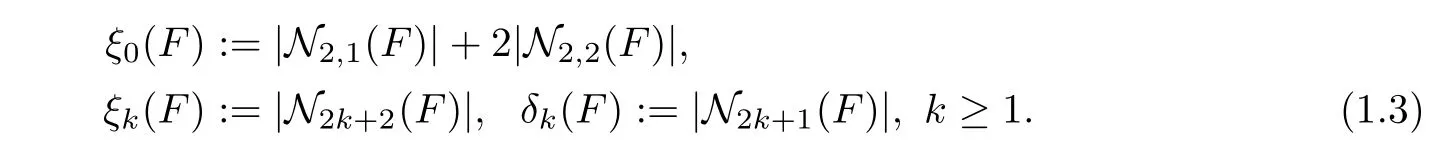
From now on,we assume that f is hyperelliptic and semistable.Let δk(f)(resp. ξk(f))be the modular invariants corresponding to Θk(resp. Ξk).Then(see[4])
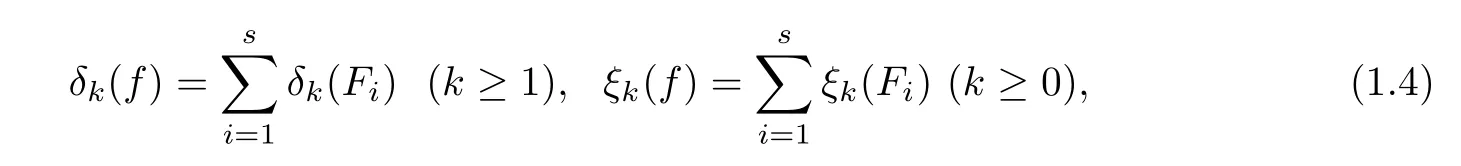
where F1,···,Fsare all singular fibers of f,and
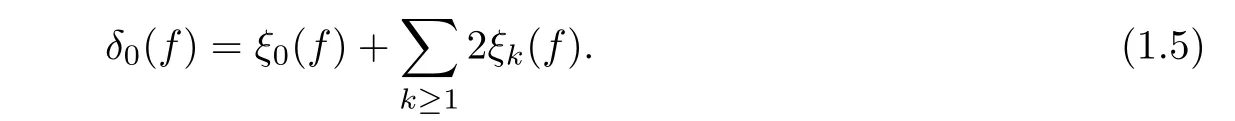
It is proved that in[4],if f is semistable,then
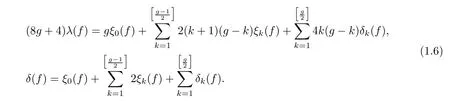
On the other hand,for a hyperelliptic fibration f:S→C,Xiao introduced the singularity indices s2(f),s3(f),···,sg+2(f)(see definition 2.6),and he obtained the following formulas(see Theorem 2.1):
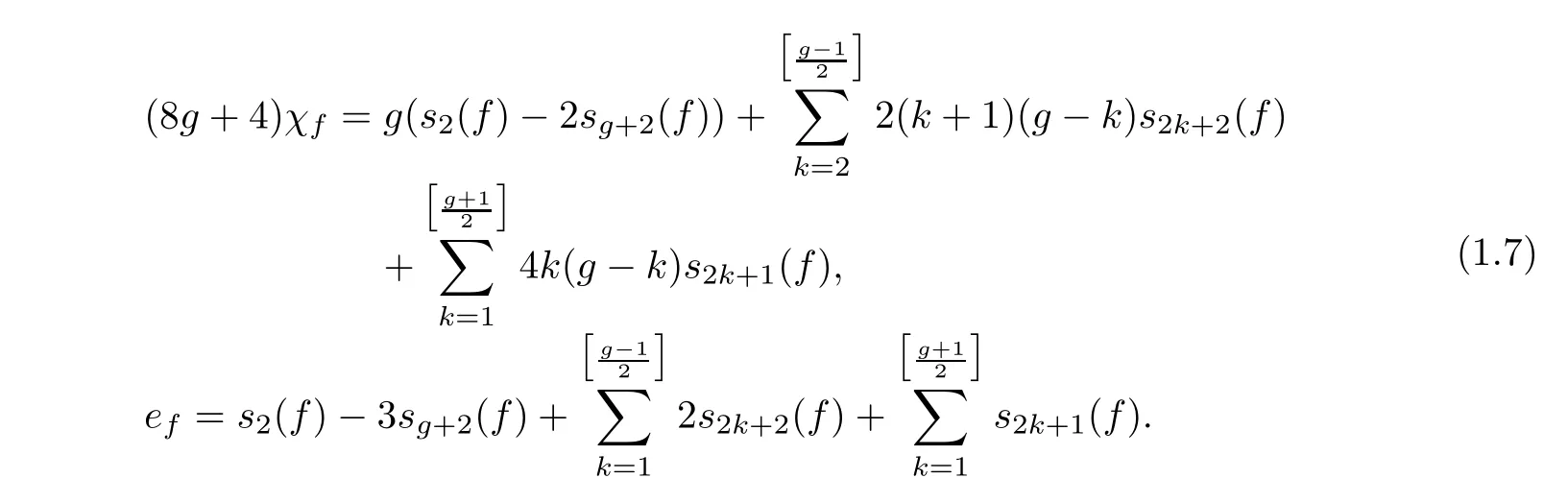
Note that Xiao’s equations do not need the semistable condition and sg+2(f)=0 if f is semistable(see Corollary 3.1).
Comparing(1.6)with(1.7),it is natural to build up the relation between modular invariants with singularity indices.
A double point p of a semistable curve F is called separable if F becomes disconnected when we normalize F locally at p;otherwise,p is called inseparable.Xiao showed that for each semistable fibration f of genus 2,s2(f)(resp.s3(f))is the number of inseparable(resp.separable)double points of all singular fibers of f(see[14]),i.e.,ξ0(f)=s2(f), δ1(f)=s3(f).
If we subdivide the inseparable nodal points into nodes of type(0,k)(k≥0),and subdivide the separable nodes into nodes of type i(i≥1),then we can get that the modular invariants δi(f),ξj(f)are the same as the singularity indices sk(f).
Theorem 1.1If f is a semistable hyperelliptic fibration of genus g≥2,then
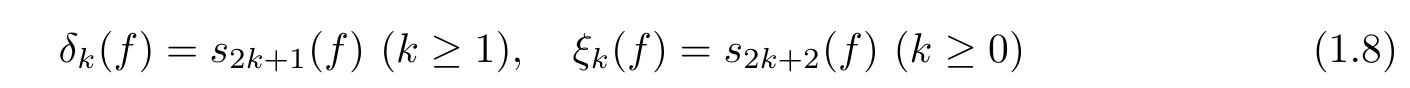
and
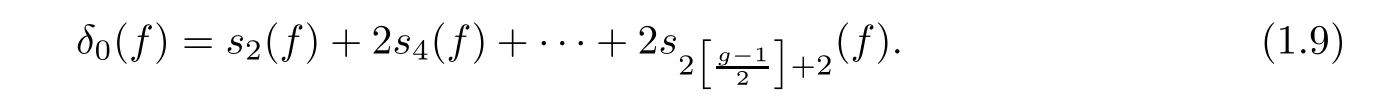
Considering the equations in(1.2)and(1.8),it is likely that there exists a more general correspondence between modular invariants and relative invariants.Precisely,we expect that if M is any kind of moduli space of curves,and η is a divisor class of M,especially the generator of Pic(M),then there is a reasonable relative invariant which coincides with the modular invariant η(f)corresponding to η for each semistable family f of curves in M.Recently,there is another such corresponding showed in[3].
In §2,we recall Xiao’s study of hyperelliptic fibration.In §3,we repeat the work(see[12])of Yuping Tu on semistable criterion,and then we prove our result locally by constructing bijective maps between sets of singularities R∗with sets of nodes(or nodal pairs)N∗.
2 Singularity Indices
2.1 Genus g data
Let P be a smooth surface,and R be a reduced even divisor(the image of R in Pic(P)is divisible by 2)on P.Let δ be an invertible sheaf such that OP(R)= δ⊗2,and we call δ the square root of R for convenience.In fact,a reduced even divisor R on P and an invertible sheaf δ with OP(R)= δ⊗2determine a unique double cover π :S → P branched along R(see[2,I.7]).Thus(R,δ)is called a double cover datum.If R is reduced smooth,then S is smooth.
If ψ1:P1→ P is a blow-up of P at a singular point x of R of order m,set
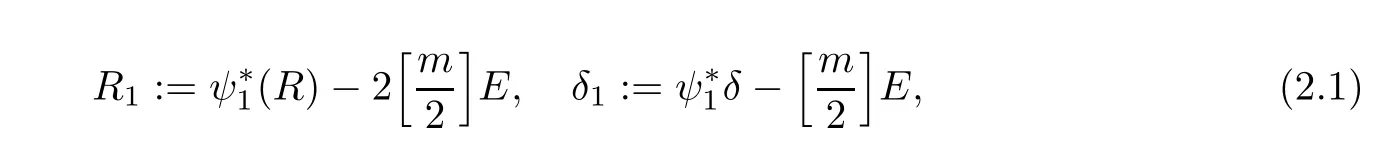
where E is the exceptional(−1)-curve of ψ1.Then(R1,δ1)is called a reduced even inverse image of(R,δ)under ψ1.In what follows,we call R1a reduced even inverse image of R brie fly,since δ1is determined by(R,δ)and R1.
definition 2.1An even resolution of R is a sequence of blow-ups=ψ1◦ψ2◦···◦ψr,
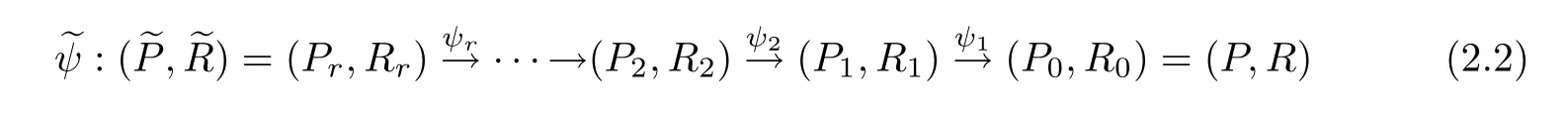
satisfying the following conditions:
(i)is a smooth reduced even divisor,
(ii)Riis the reduced even inverse image of Ri−1under ψi.
Furthermore,is called the minimal even resolution of the singularities of R if
(iii) ψiis the blow-up of Pi−1at a singular point xiof Ri−1for any 1 ≤ i≤ r.
If the even resolution of:→P of R is minimal,then for any even resolution ψ?:P?→P,there exists a morphism α:P?→P such that α(R?)=,α(δ?)=.Here α(δ?)=means that there exists a divisor D?∈Pic(P?)with δ?OP?(D?)such thatO?P(α(D?)).Note that the minimal even resolution is unique.
If xi∈ Pi−1lies in Ej(j
Unless stated otherwise,the singularities(resp.smooth points)of R include all the in finitely near singularities(resp.smooth points)of Riin Pifor 1≤i≤r.If we want to specify a singularity(resp.smooth point)p of R,we will point out the surface which p lies in.
Now we want to introduce the genus g datum associated to a hyperelliptic fibration f:S→C,according to Xiao’s approach in[13–14].
Since the generic fiber F of f is hyperelliptic,we glue the involution σFof F together,and then we get a rational map σ :S → S.The map σ is in fact a morphism,because f is assumed to be relatively minimal.Let ρ:→ S be the minimal composition of blow-ups of S at all the isolated fixed points of σ,and:→be the induced map of σ onThen=is smooth.Let:→be the corresponding double cover branched along a smooth reduced divisorin.Then(O?S)O?P⊕,whereis an invertible sheaf with
Let ΦK:S???Proj(f∗ωCS)be the relative canonical map,then ΦKis a generic double cover,for its restriction on a generic fiber F is the double cover induced by σF.Let:→S be the minimal composition of blow-ups at all base points of ΦKand all isolated fixed points.Then the birational morphism→is an isomorphism because of the minimality of ρ.Hence=ρ and.This gives another process to get the double coverθ:→and the branch locus.

The morphism:→C induced by f is a birational ruling(a fibration whose general if bers are rational curves).There are many choices to give a birational morphism:→P mapping to a geometric ruled surface P.The morphisminduces a reduced divisor R=in P.All such geometric ruled surfaces differ by elementary transforms.We want to choose one such that R2is the smallest.
In the rest,a curve D means a nonzero effective divisor.
definition 2.2Let D be an irreducible curve on a fibred surface S with fibration f:S→C.If f(D)is a point,we call D a vertical curve.
Lemma 2.1(see[13,Lemma 6])There is a birational morphism:→P over C,where every fiber of the induced morphism ϕ:P→C is P1,such that,letting δ be the image ofin P,and Rhbe the sum of the non-vertical irreducible components of R.Then R2is the smallest among all such choices,and the singularities of Rhare at most of order g+1.Therefore as R is reduced,the singularities of R are of order at most g+2,and if p is a singular point of order g+2,R contains the fiber of ϕ passing through p.
definition 2.3Let P be a geometric ruled surface over C,and(R,δ)be a double cover datum on P.If(R,δ)satisfies that RΓ =2g+2,where Γ is a generic fiber of ϕ :P → C,and the order of any singularity of the non-vertical part Rhof R is at most g+1,then we call(P,R,δ)a genus g datum.
We have shown that there is a genus g datum(P,R,δ)(Lemma 2.1)associated to a given hyperelliptic fibration f.On the other hand,let(P,R,δ)be a genus g datum over a smooth curve C,:→P be the minimal even resolution of(P,R),and:→be the double cover determined by.Let ρ :→ S be the morphism of contracting all the vertical(−1)-curves,then we get a hyperelliptic fibration f:S → C.Hence we need to study the vertical(−1)-curves in.
Lemma 2.2(see[14])Let(P,R,δ)be a genus g datum,and Γ be any fiber of P → C,whose inverse image inis a(−1)-curve.In other words,the strict transform of Γ inis a(−2)-curve contained in.If g is even,then one of the following two cases is satisfied:
(1)Rhintersects with Γ at two distinct points x,y,mx(Rh)=my(Rh)=g+1;or
(2)Rhintersects with Γ at one point,and the point is a singularity of type(g+1 → g+1)(see definition 2.4),which is tangent to Γ.
If g is odd,then Rhintersects with Γ at one point,and it is a singularity of type(g+2→g+2),which is tangent to Γ.
Lemma 2.3(see[14])Suppose that E is a vertical(−1)-curve in,then the imageof E inis an isolated(−2)-curve contained in,andeither comes from a blow-up of a singularity of R with odd order,or is a strict transform of a fiber in Lemma 2.2.Conversely,for any singularity of R with odd order or any fiber in Lemma 2.2,there is a corresponding vertical(−2)-curve.
Remark 2.1As stated in[13],if we start from a hyperelliptic fibration f:S→C,we can choose a genus g datum(P,R,δ)such that R2is the smallest,and then the case(1)in Lemma 2.2 does not occur.Accordingly,Lemma 2.3 turns to be Lemma 7 in[13].In what follows,we always assume that the genus g datum associated with f satisfies that R2is the smallest.
Consequently,we only need to consider genus g datum for hyperelliptic fibrations.
2.2 Singularity indices
Based on the above preparation,we are able to define the singularity indices.
Let(P,R,δ)be a genus g datum over a smooth curve C,andin(2.2)be the minimal even resolution of(P,R).We decomposeinto ψ?:→followed by:→P,where ψ?andare composed respectively of negligible and non-negligible blow-ups.We may assume=ψ1◦···◦ψtfor t≤r.Denote bythe reduced even inverse image of(R,δ)inP
definition 2.4Let xibe a singularity of Ri−1of order 2k+1If Rhas
ia unique singularity on the inverse image of xi,say xi+1,with order 2k+2,then we call xia singularity of type(2k+1→2k+1).
definition 2.5Let f:S→C be a fibration and D be a reduced curve on S.Let φ:D→C be the natural morphism induced by f.Let ν :→D be the normalization of D,Dhbe the union of all the irreducible components ofwhich maps projectively onto C,and νh:Dh→ D be the induced map.The ramification index r(D)of φ is defined as follows:
If q ∈ Dhis a ramification point of φ ◦ νh,then the ramification index rq(D)is defined as usual.
If p is a singularity of D of order mp,then the ramification index is rp(D)=mp(mp−1).
If E is an isolated vertical curve of?D,then the ramification index is rE(D)=χtop(E).
Furthermore,we define
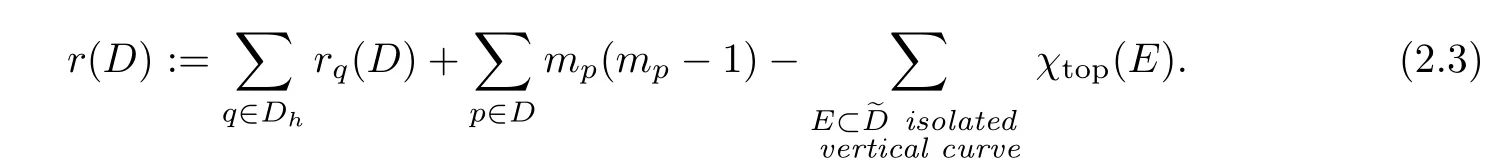
Remark 2.2It is easy to see that r(D)=D2+from the adjoint formula KSD+D2=−2χ(O(D))(see[14]).
When we consider a singular fiber F of f,the singularities and ramification points of branch locus are those over f(F)if there is no confusion.
definition 2.6(see[13–14])Let f:S → C be a hyperelliptic fibration,and(P,R,δ)be the corresponding genus g datum.Suppose that F is a singular fiber of f.We denote by Γ the fiber of P→C over f(F).The singularity indices sk(F)(2≤k≤g+2)are defined as follows.
(1)Let E1,···,Ekbe all the isolated vertical(−2)-curves in.Letting=−E1−···−Ek,then s2(F)is defined to be the ramification index ofover the point f(F).Concisely,if we denote by R2,1(F)the set of all ramification points ofover f(F),by R2,2(F)the set of all singularities of,and by R2,−(F)the set of all vertical components in,then
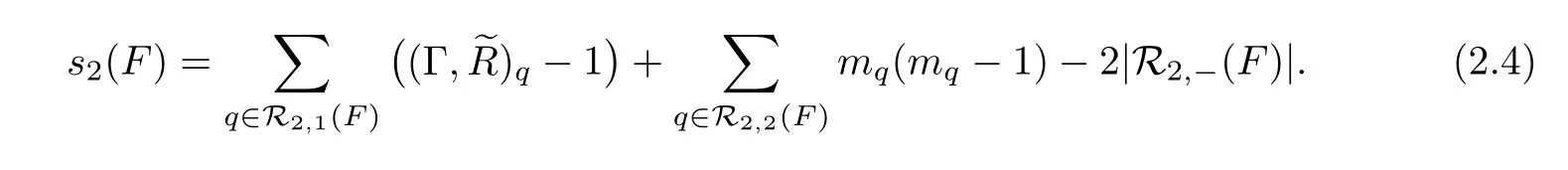
(2)If k is odd,denote by Rk(F)the set of all singularities of R of type(k→k),then sk(F):=|Rk(F)|.
(3)If k≥4 is even,denote by Rk(F)the set of all singularities of R of order k,not belonging to a singularity of type(k+1→k+1)or(k−1→k−1),then sk(F):=|Rk(F)|.
define

where F1,···,Fsare all the singular fibers of f.
Remark 2.3Xiao introduced the singularity indices in order to compute the contribution of singular fibers to the invariants,χf.It is convenient to put xi,xi+1in definition 2.4 together,and regard the pair{xi,xi+1}of points as one singularity of type(2k+1→2k+1),that is,the total contribution of xiand xi+1to singularity indices adds one to s2k+1only.
Example 2.1Let(x,t)be the local coordinate of P1× Δ,where Δ is the open unit disc of C.Let
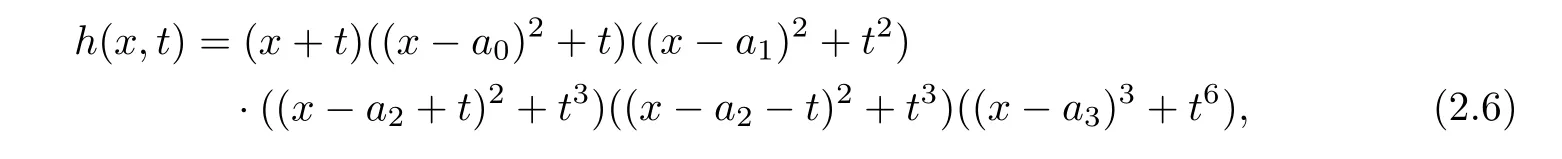
where ai’s are distinct nonzero complex numbers.Let f:SΔ→ Δ be the local fibration of genus g defined by y2=h(x,t).Let F=f−1(0)be the fiber of f over the origin,and Γ be the fiber of P1×Δ→Δ over the origin.
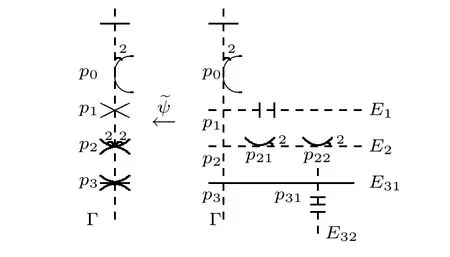
Figure 3 The minimal even resolution
The branch locus is R={(x,t)∈ P1×Δ :h(x,t)=0},and RΓ?=12,where Γ?is the generic fiber of P1×Δ→Δ.Hence g=5 by Riemann-Hurwitz formula.Let pi=(ai,0)(i=0,1,2,3),then p2and p3are non-negligible.
Let p21and p22be the in finitely near points of p2,which are smooth points of.Let p31be the in finitely near singularity of p3,then{p3,p31}is a singularity of type(3→3).Therefore=R which is the strict transform in,and
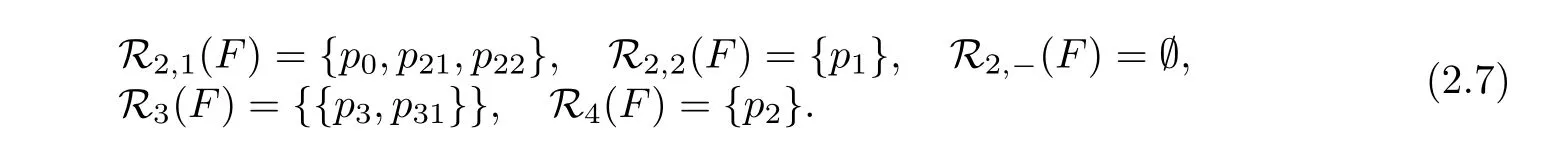
Furthermore,the singularity indices are

Using the singularity indices,Xiao obtained the following formulas.
Theorem 2.1(see[14,Theorem 5.1.7])Let f:S→C be a hyperelliptic fibration of genus g,then
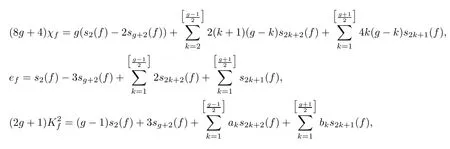
where ak=6((k+1)(g−k)−4g−2)and bk=12k(g−k)−2g−1.
Corollary 2.1(see[14])If f is hyperelliptic,then the slope of f
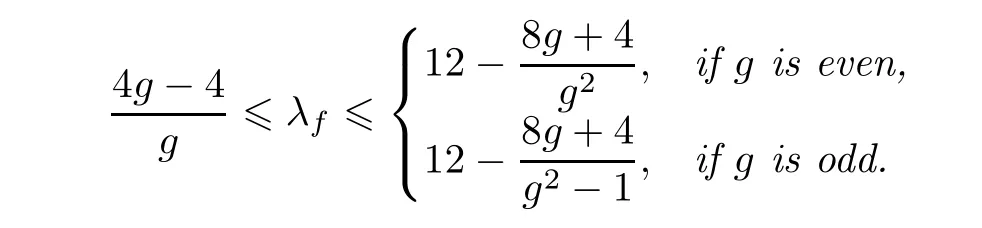
Moreover,the left equality holds if and only if s2(f)0,sk=0(k>2),and the right equality holds if and only ifand the rest singularity indices are all zero.
3 Modular Invariants in Semistable Case
At the beginning of this section,we fix notations firstly.
Let(P,R,δ)be a genus g datum over a smooth curve C,andin(2.2)be the minimal even resolution.Let f:S→C be the fibration determined by the datum,and F be a singular fiber of f.Denote bythe total transform of F by ρ:→ S,which is a birational morphism contracting all the vertical(−1)-curves.Let Γ be the fiber of ϕ :P → C over t=f(F),and we call Γ the image of F in P brie fly.Let=(Γ)be the total transform of Γ by the minimal even resolution:→P of R.To keep it simple,we also denote by R(resp.Γ)the strict transform of R(resp.Γ)under the even resolution
Denote by B=(Γ)the inverse image of Γ in,and by Bi=?θ−1(Ei)the inverse image of the exceptional curve Ei.Then B(resp.Bi)may be composed by two irreducible curves B?and B??(resp.and).Letting
then
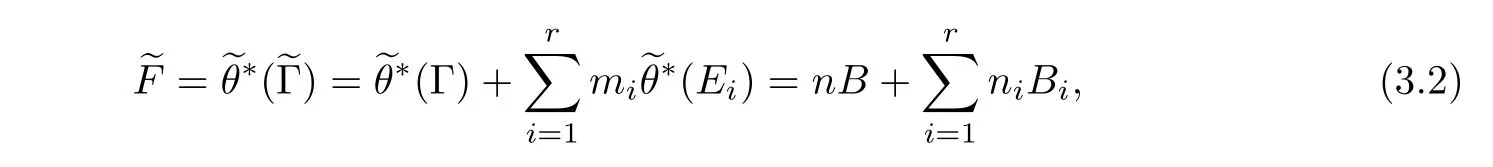
where n=1,2 and ni=mior ni=2mi.Therefore,F=is obtained by contracting(−1)-curves in
definition 3.1An even resolution at point p of R is a sequence of blow-ups=ψ1◦ψ2◦···◦ ψl
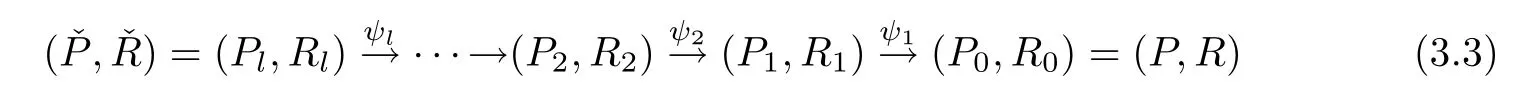
satisfying the following conditions:
(i)All the points ofˇR in finitely near p,including p,are smooth.
(ii)Riis the reduced even inverse image of Ri−1under ψi.
Furthermore,is called the minimal even resolution at p if
(iii) ψiis the blow-up of Pi−1at a singular point piof Ri−1,which is in finitely near p,for any 1≤i≤l.
If the resolutionis minimal,we call the desired number lpof blow-ups the length of the minimal even resolutionat p.The exceptional curves Ei’s(1≤i≤l)in Plare called exceptional curves from p brie fly.For example,if p is an ordinary singularity of even order,then lp=1;if p is a singularity of type(3→3),then lp≥2.
Let p be a singularity of R,and E1,···,Elpbe all the exceptional curves from p in Plp.Set Ep:=m1E1+···+mlpElp,Bp:=(Ep),where mi=multEi(Ep)=multEi.Then we call Epthe block offrom p,and call Fp:=ρ(Bp)the block of F from p.Assume that Γ is not contained in R.Let p1,···,pebe all the singularities of R on Γ in P,and Bp0=(Γ).Then we can decompose F into finite blocks F=Fp0+Fp1+···+Fpe,and we call this decomposition the modular decomposition of F.
Example 3.1(Continuation of Example 2.1)Let f:SΔ→ Δ be the local fibration in Example 2.1.Then lp1=1,lp2=1,lp3=2.The blocks ofare Ep1=E1,Ep2=E2,Ep3=E31+E32.
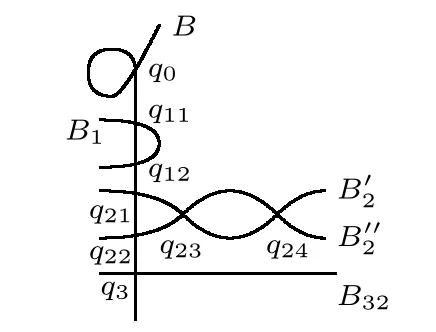
Figure 4 Modular decomposition of F
Here E1,E2,E32are not contained in?R,and E31is contained in?R.Then the blocks of F are Fp0=B,Fp1=B1,Fp2=+,Fp3=B32.In these equations,B is a rational curve with a node q0;B1is P1meeting B at two points q11,q12;andare both P1meeting with B at q21,q22respectively and meeting with each other at two points q23,q24;and B32is a smooth elliptic curve meeting with B at q3.Then F is semistable,and the modular decomposition of F is=B+B1+(+)+B32.
3.1 Semistable criterion
There is a criterion for semistable hyperelliptic fiber given by Tu[12].We rewrite the result and its proof here,because the reference is in Chinese.
Lemma 3.1(see[12])If F is a semistable singular fiber of a hyperelliptic fibration f:S→C,then we have the following results:
(1)If g is odd,then Γ is not contained in R;if g is even and Γ is contained in R,then Γ is the fiber in Lemma 2.2.
(2)If p is a smooth point of R in P,then the intersection number of R with Γ at p is(R,Γ)p≤ 2.
(3)If p is a singularity of R in P,then we have(R,Γ)p=ordp(R).
(4)Let q∈Ri(i≥1)be an in finitely near singularity,then there is exactly one exceptional curve Eqpassing through q,and(R,Eq)q=ordq(R).
(5)Let q∈Riand Eqbe the same as(4).If ordq(R)=l is even,then Eqis not contained in?R.If ordq(R)=l is odd,then either Eqis contained inand thus Eqis from a singularity of type(k→k)(k is odd,k≥l);or Eqis not contained in,and thus q is a singularity of type(l→l).
(6)Let q be an in finitely near smooth point,and Eqbe the irreducible component passing through q,then(R,Eq)q≤2 and Eqis not contained in.
Proof(1)Suppose Γ ⊆.Then B is a component of?F with multiplicity 2,for π∗(Γ)=2B,furthermore,B2=.If Γ2≤ −4,then B2≤ −2.Hence B is a multiple component inwhich can not be contracted,contradicting with the assumption that F is semistable.Thus we get that if Γ ⊆then Γ is a(−2)-curve in.If g is odd,then any singularity of R is of type(g+2 → g+2),and we need twice blow-up so that the intersection point of Γ with the exceptional curve is a smooth point of R.Hence there is a(−1)-curve,say E2,with multiplicity 2 in.It is easy to see that E2is not contained in,and π∗(2E2)=2B2in F is irreducible with≤−2.Therefore B2is an un-contractible multiple component in semistable curvewhich is impossible.So when g is odd,Γ is not contained in R.
(2)In what follows,we may assume that Γ is not contained in R since(1).Let n=(R,Γ)p,we take the local coordinate(x,t)of p such that the local equations of Γ and R near p are t=0 and t+xn=0 respectively.Then the local equation of F in S is y2−xn=0.If n≥3,it is a singularity of type An−1on F,and thus F is not semistable.
(3)Suppose not,then(R,Γ)p>ordp(R).Let ψ1be the blow-up at p,and E1be the exceptional curve.Then the intersection point p?of Γ with E1is still on R.Let ψ2be the successive blow-up at p1and E2be the exceptional curve.Then the total transform of Γ by ψ1◦ψ2is=Γ+2E2+E1,and B2is with multiplicity at least 2 in F.Hence B2is a(−1)-curve in,E2is a(−2)-curve in,and p1is a singularity of type(k → k)(k is odd)(see Lemma 2.2).Furthermore,there is a singularity p2on E2of order k+1.Let ψ3be the blow-up at p2with exceptional curve E3.Then=Γ+2E3+2E2+E1,E3is not contained in,and B3is an un-contractile multiple component in.
(4)Suppose that E1and E2are both through q.When ordq(R)is even,then the exceptional curve E3of the blow-up at q is of multiplicity at least 2,and E3is not contained in.So B3is an un-contractile multiple component in F.When ordq(R)=k is odd,then q should be of type(k→k),and E3is contained inwith multiplicity at least 2.Blowing up the in finitely near singularity q?of q,then the exceptional curve E4is not contained inof multiplicity at least 2,which is impossible.The proof of the second part of(5)is analogous to that of(3).
(5)Suppose that ordq(R)is even and Eqis contained in?R,then ordq(Ri)is odd.The exceptional curve E?of the blow-up ψ :Pi+1→ Piat q is contained in?R.Thus≤ −2 in,and≤ −4 in.So Eqcorresponds to an un-contractile multiple component in F.Consequently,we proved the first part of(4).The second part of(4)is a direct corollary of Lemma 2.3.
(6)The proof of the second part is the same as that of(1),and the rest is the same as that of(2).We omit the detail.
Remark 3.1Let F be a semistable fiber of f,and p be a singularity of R.Then there is exactly one irreducible component Eppassing through p.We call Epthe exceptional curve through p.Note that Epis either Γ or an exceptional curve.
Corollary 3.1If F is a semistable hyperelliptic fiber of genus g,then sg+2(F)=0.
ProofBy Lemma 3.1(1),we know that if g is odd,then sg+2(F)=0;if g is even,then Γ is the fiber in Lemma 2.2,and we can check the result directly.
3.2 Proof of Theorem 1.1
We first consider the effect of the smooth points of R to the arithmetic genus.
Lemma 3.2Let F be a semistable fiber of f.Assume that the image Γ of F in P is not contained in R.Suppose that all the intersection points p1,···,pk1,q1,···,qk2of R with Γ are smooth,where(Γ,R)pi=2 and(Γ,R)qj=1.
(1)If k20,then F is an irreducible curve with k1nodes corresponding to pi’s,the g
eometric genus of F isand
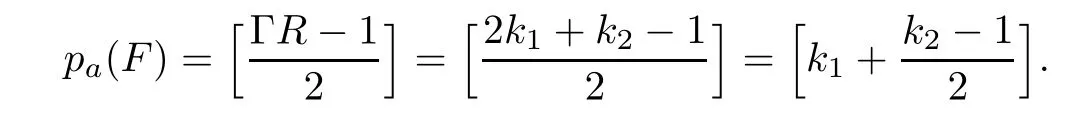
(2)If k2=0,then F is composed of two smooth rational curves which meet with each other at k1distinct points.Thus
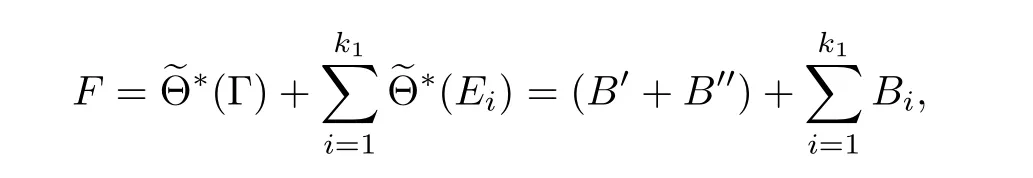
where every irreducible component is a smooth rational curve,Bimeets B?and B??normally at one point respectively for each 1≤i≤k1,and there is no other intersection.Hence
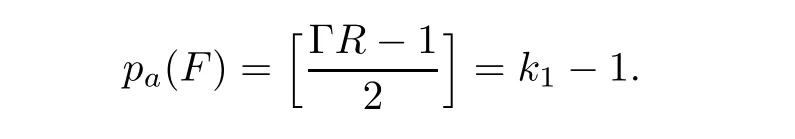
ProofThe proof is obvious,and we omit it.
Then we consider the effect of singularities.
Lemma 3.3Suppose that F is a semistable fiber of f,and the image Γ of F in P is not contained in R.If p is a singularity of R such that the exceptional curve Epthrough p is not contained in the branch locus,then the arithmetic genus of the block Fpof F from p is
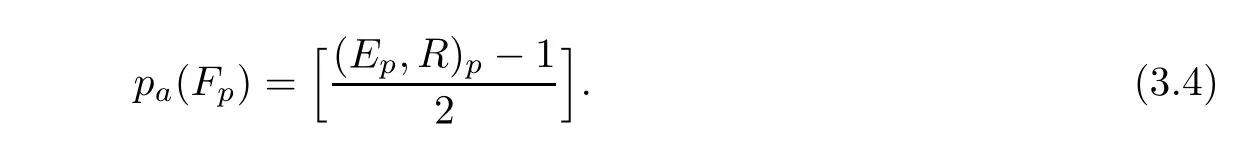
ProofWe use induction on the length lpof the minimal even resolutionof R at p.Note that=k,and ord(R)=(R,E)for any singularity of R on Efrom
ppppLemma 3.1.We may assume that Epis Γ,since the proof for exceptional curves is similar.
If lp=1,then ordp(R)=2k+2 is even and p is an ordinary singularity.The exceptional curve E1from p is not contained in R,and E1meets R in P1transversely at 2k+2 distinct points.Hence Ep=E1,and Bp=B1with pa(B1)=k.
If lp=2 and ordp(R)=2k+2 is even,then there is exactly one in finitely near singularity p1of R in P1,which is an ordinary singularity of even order,say 2k2.Hence E1,E2are not contained in R,Ep=E1+E2,and Epmeets R in P2transversely at 2k+2 distinct points.Let E1R=2k1+2,then k1+k2=k.Thus pa(B1)=k1,pa(B2)=k2−1,and B1intersects with B2at two points transversely.So pa(Fp)=pa(Bp)=pa(B1)+pa(B2)+1=k.
If lp=2 and ordp(R)=2k+1 is odd,then p is a singularity of(2k+1→2k+1).So E1is contained in R,E2is not contained in R,and Ep=E1+E2,where E2meets R2in P2transversely at 2k+2 distinct points.It is easy to see that B1is a(−1)-curve and B2is a smooth curve with genus k.Hence pa(Fp)=pa(B2)=k.
Assume that(3.4)holds for any positive integer l If ordp(R)=2k+1 is odd,let ψ1:P1→ P be the blow-up at p.Then there is exactly one in finitely near singularity q of R in P1,and(R,E1)q=2k+1,ordq(R1)=2k+2.Let ψ2:P2→ P1be the successive blow-up at q.It is clear that E1is contained in R,but E2is not. Let q1,···,qαbe all the in finitely near singularities of q in P2.Hence lqi Hence It is easy to see that in,=(R,E2)sm+(α − β)+1.By Lemma 3.2, The block offrom p isCombining(3.5)and(3.6),then where the block Fqiintersects with B2at two points,and adds one to the arithmetic genus for each 1≤ i≤ β.Here we used the induction assumption. If ordp(R)=2k+2 is even,take ψ1:P1→ P,the blow-up at p.Let q1,···,qαbe all the in finitely near singularities of p on p1.Then the rest of the proof is the same as the odd case above. Now we can prove the identities between singularity indices(definition 2.6)with modular invariants δi(F), ξj(F)(see(1.3)–(1.5)). Theorem 3.1Let f:S→C be a semistable hyperelliptic fibration of genus g,and F be a singular fiber of f,then Proof(1)Proof of s2k+1(F)= δk(F),k≥ 1. We define a bijective map between sets as follows. If p∈R2k+1(F),then Ep(the exceptional curve through p)is not contained in.Let=+Ep,where Epis the block of?Γ from p.Then the decomposition of F is F=+Fp,where pa(Fp)==k,andintersects withat a point,say q,which is a node of type k.We define α2k+1(p)=q ∈ N2k+1(F),then α2k+1is well-defined. On the other hand,if q∈N2k+1(F),then F consists of a genus k curve Fqand a genus g−k curve,and Fqmeetsat q transversely.Then q is an isolated fixed point of the hyperelliptic involution σ.Thus the inverse image of q inunder ρ :→ S is a(−1)-curve B.Henceis a(−2)-curve contained inwhich is from a singularity,say p,of type(2k?+1→2k?+1)(see Lemma 2.3 and Lemma 3.1(4)).Since(Ep)=ρ∗(Fq),the arithmetic genus of the block of F from p is k?=pa((Ep))=pa(Fq)=k.Thus p∈R2k+1(F),and α2k+1(p)=q.Hence it is clear that α2k+1is surjective and injective. Therefore,s2k+1(F)=|R2k+1(F)|=|N2k+1(F)|=δk(F). (2)Similar proof of s2k+2(F)= ξk(F),k ≥ 1. We define a bijective map between sets as follows. If p∈R2k+2(F),then Epis not contained in,and the exceptional curve E1of the blow-up at p is not in?R either.Hence(p)consists of two points q and σ(q).Let=Ep+,then F=Fq+,pa(Fq)=k and Fqmeetsat q and σ(q)transversely.So the nodal pair{q,σ(q)} ∈ N2k+2(F).Hence we are able to define α2k+1(p)={q,σ(q)}. On the other hand,if{q,σ(q)} ∈ N2k+2(F),then F=Fq+,where pa(Fq)=k,and they intersect with each other at two points q and σ(q)transversely.We may assume that?F=Fq+,which meet at q and σ(q).Then=,say p,is an intersection point of two curves not in?R.Hence we can decomposeas=Ep+,where REp=2k+2 and Epmeetsat p only.The curve Epis from a singularity of order ordp(R)=REq=2k+2.Therefore,p is the inverse image of{q,σ(q)}under α2k+2,and α2k+2is bijective. So s2k+2(F)=|R2k+2(F)|=|N2k+2(F)|=ξk(F). (3)Proof of s2(F)=ξ0(F). If E is a vertical components of,then B=(E)is a multiple component of.So B is a(−1)-curve for F is semistable,and then we know that E is a(−2)-curve inHenceis the strict transform of R in,and|R2,−(F)|=0. If p∈R2,1(F),then p is a smooth point of R,(R,Ep)p=2,rp(R)=1,and(p)is an α-type node q.Conversely,each α-type node q is a singularity p of type A1whose local equation is t+x2=0.So we get a bijective map If p∈R2,2(F),then p is an ordinary double point,and rp(R)=2.By the same discussion in(2),we can obtain a bijective map Hence s2(F)=|R2,1(F)|+2|R2,2(F)|=|N2,1(F)|+2|N2,2(F)|=ξ0(F). Proof of Theorem 1.1It is a corollary of the above theorem. Remark 3.2Let f:S→C be a hyperelliptic fibration of genus g≥2,and:→be a semistable model of f.Then by Corollary 2.1 and Theorem 1.1,we know thathas the lowest slope if and only if the image[f]of f by the moduli map intersects with Ξ0only,andhas the highest slope if and only if[f]intersects withonly.See[7]for families with the highest slope. Example 3.2(Continuation of Example 3.1)From the analysis of the blocks of F in Example 3.1,we can easy to know that pa(Fp1)=1,pa(Fp2)=1,pa(Fp3)=1,and the sets of nodes are Hence the numbers of nodes on F are Comparing these equations with(2.7)and(2.8),we give an example for Theorem 3.1. AcknowledgementsI would like to thank Prof.Sheng-Li Tan and Prof.Jun Lu for their interesting and fruitful discussions.Thanks to Fei Ye for reading the preliminary version of this paper and making many valuable suggestions and discussions.Finally,I wish to thank the referees for their suggestions,which greatly improved the exposition of this paper. [1]Arbarello,E.,Cornalba,M.and Griffiths,P.A.,Geometry of Algebraic Curves,Vol.II,Springer-Verlag,Berlin Heidelberg,2011. [2]Bath,W.,Peters,C.and Van de Ven,A.,Compact Complex Surfaces,Springer-Verlag,Berlin Heidelberg,1984. [3]Chen,Z.,Lu,J.and Tan,S.-L.,On the modular invariants of a family of non-hyperelliptic curves of genus 3,http://math.ecnu.edu.cn/preprint/2010-006.pdf [4]Cornalba,M.and Harris,J.,Divisor classes associated to families of stable varieties,with applications to the moduli space of curves,Ann.Scient.Ec.Norm.Sup.,21,1988,455–475. [5]Horikawa,E.,On algebraic surfaces with pencils of curves of genus 2,Complex Analysis and Algebraic Geometry,Cambridge Univ.Press,London,1977,79–90. [6]Kodaira,K.,On compact analytic surfaces,III,Ann.Math.,78(1),1963,1–40. [7]Liu,X.L.and Tan,S.L.,Families of hyperelliptic curves with maximal slopes,Science China Mathematics,56(9),2013,1743–1750. [8]Namikawa,Y.and Ueno,K.,The complete classification of fibres in pencils of curves of genus two,Manuscripta Math.,9,1973,143–186. [9]Ogg,A.P.,On pencils of curves of genus two,Topology,5,1966,355–362. [10]Tan,S.L.,Chern numbers of a singular fiber,modular invariants and isotrivial families of curves,Acta Math.Viet.,35(1),2010,159–172. [11]Tan,S.L.,Chern numbers of holomorphic foliations and Poincaré problems,in preprint. [12]Tu,Y.,A criterion of semi-stable hyperelliptic fibration,Journal of Sichuan University(Natural Science Edition),45(5),2008,1049–1050(in Chinese). [13]Xiao,G.,π1of elliptic and hyperelliptic surfaces,Internat.J.Math.,2(5),1991,599–615. [14]Xiao,G.,The fibrations of algbraic surfaces,Shanghai Scientific&Technical Publishers,Shanghai,1992(in Chinese). [15]Zhang,S.,Admissible pairing on a curve,Invent.Math.,112(1),1993,171–193. [16]Zhang,S.,Gross-Schoen cycles and dualising sheaves,Invent.Math.,179(1),2010,1–73.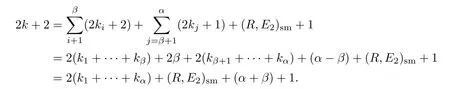
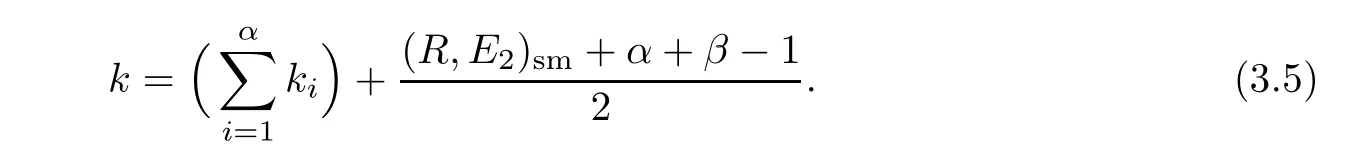
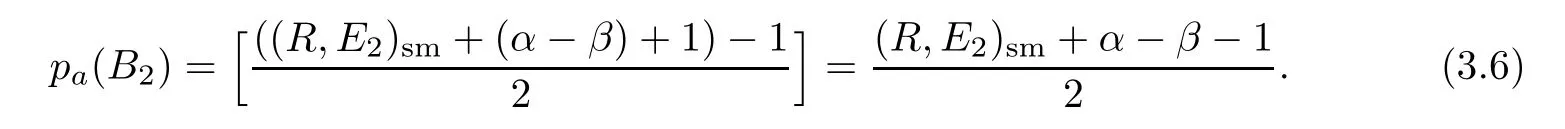
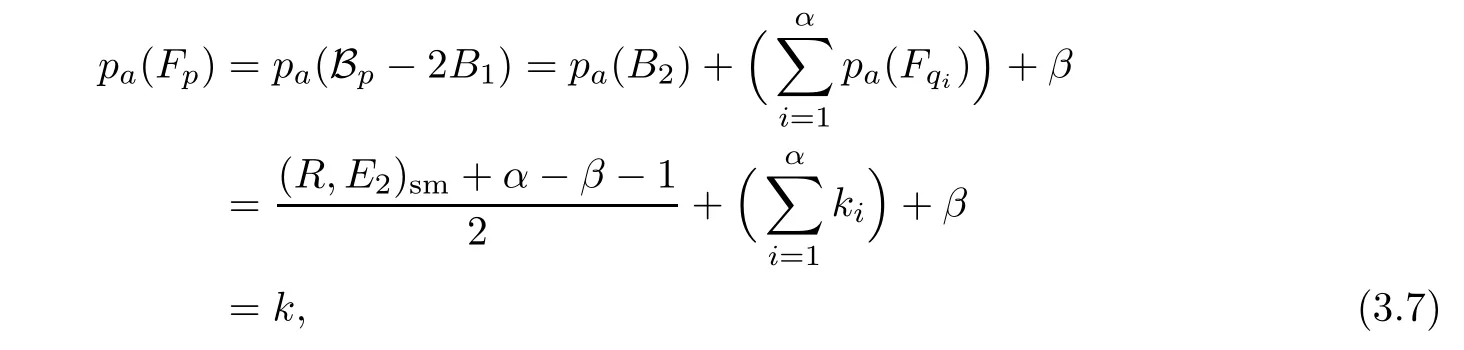
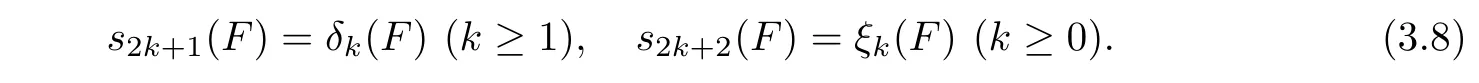
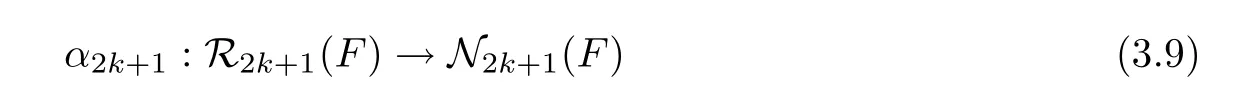
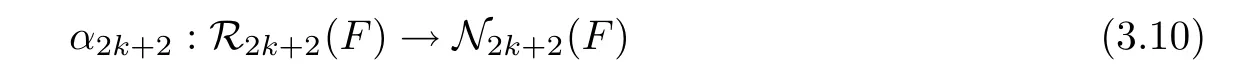


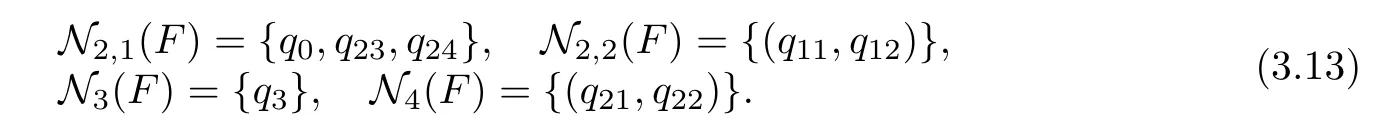
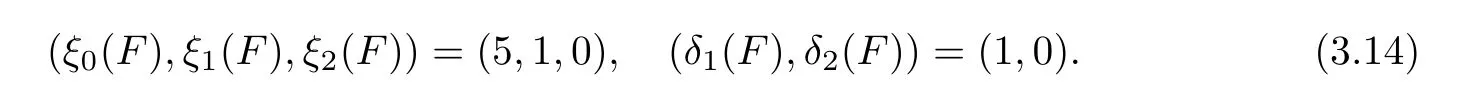
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Revuz Measures,Energy Functionals and Capacities Under Girsanov Transform Induced by α-Excessive Function∗
- On the Same n-Types for the Wedges of the Eilenberg-Maclane Spaces∗
- Double Biproduct Hom-Bialgebra and Related Quasitriangular Structures∗
- The 3D Non-isentropic Compressible Euler Equations with Damping in a Bounded Domain∗
- On Robustness of Orbit Spaces for Partially Hyperbolic Endomorphisms∗
- New Quantum MDS Code from Constacyclic Codes∗
