Asymptotic Behavior of the Incompressible Navier-Stokes Fluid with Degree of Freedom in Porous Medium∗
2016-06-05HongxingZHAOZhenganYAO
Hongxing ZHAO Zhengan YAO
1 Introduction
Homogenization is a mathematical tool that allows changing the scale in problems containing several characteristic scales.Typical examples of its utilization are finding effective models for composite materials,in optimal shape design,etc.Another important example,which we are interested in,is the fluid mechanics of the flow through porous medium.
In porous medium,there are at least two length scales:A microscopic scale and a macroscopic scale.Quite often,the partial differential equations describing a physical phenomenon are posed at the microscopic level whereas only macroscopic quantities are of interest for the engineers or the physicists.Therefore,effective or homogenized equations should be derived from the microscopic ones by an asymptotic analysis.To this end,it is convenient to assume that the porous medium has a periodic structure.
A number of known laws from the dynamics of fluids in porous media were derived using homogenization.The most well-known example is Darcy law,being the homogenized equation for one-phase flow through a rigid porous medium.Its formal derivation by two-scale expansion goes back to the classical paper by Sanchez-Palencia[1],Keller[2]and the classical book Bensoussan[3].It was rigorously derived by using oscillating functions by Tartar[4].In other cases of periodic porous media,we refer the readers to the papers by Allaire[5–7]and Mikelic[8–9].Other works can be seen in[10–11]and the references therein.
Besides the Darcy law,Brinkman[12]introduced a new set of equations,which is called the Brinkman law,an intermediate between the Darcy and Stokes equations.The so-called Brinkman law is obtained from the Stokes equations by adding to the momentum equation a term proportional to the velocity(see[6]).
In this paper,we are interested in obtaining the homogenized result for the Navier-Stokes fluid with degree of freedom in porous medium.This model problem was proposed by Lions[13],where he proved the existence and the regularity of the solutions.
Before stating the system,let us recall the domain we consider.A porous medium is defined as the periodic repetition of an elementary cell of size εin a bounded domain Ω of Rnwith n=2,3.The solid part of the porous medium is also taken of size ε.The domain Ωεis then defined as the intersection of Ω with the fluid part.We consider an incompressible fluid governed by the Navier-Stokes equations with degree of freedom.So,we have the following equations:
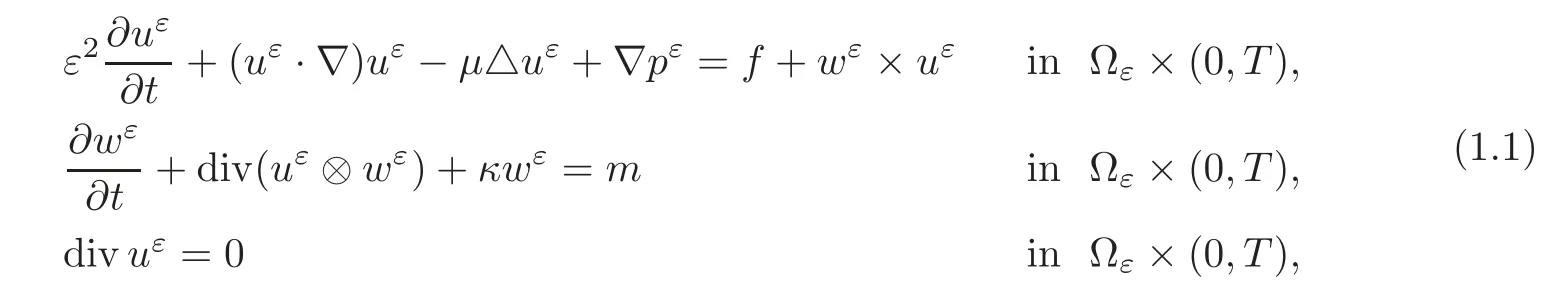
where uε,pε,wεare the unknown quantities velocity,pressure and degree of freedom of the fluid,respectively,f∈L2(Ω×(0,T))is the external force.
The system is supplemented with the boundary condition and initial conditions as follows:
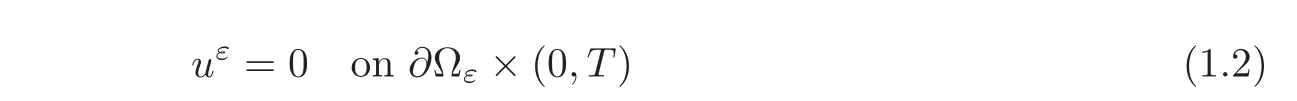
and

whereare bounded in L2(Ωε).
Our aim here is to investigate the asymptotic behavior of uε,pε,wεas ε→ 0+under the assumptions mentioned above.The main difficulty here is how to pass the limit in the momentum equations.To overcome this obstacle,we need to revise the estimates on the inertia and extend the pressure to the whole domain.It is resolved by using the general Poincaré’s equality in porous medium(see[11]).
The paper is organized as follows.In Section 2,we list some useful results and state the main results in this paper.In Section 3,we give priori estimates of the unknowns and extend them to the whole domain.In Section 4,we prove the main result in this paper.
2 Notations,Preliminaries and Main Results
The structure of a porous medium is standard(see[4–5,8]).To give a good understanding for the readers,we write it detail again.Let Ω be an open bounded subset of Rnwith n=2 or 3 and define Y=[0,1]nto be the unit open cube of Rn.Let Ysbe a closed smooth subset of Y with a strictly positive measure.The fluid part is then defined by Yf=Y −Ys.Let θ =|Yf|.The constant θ is called the porosity of the porous medium.We assume that 0< θ<1.
Repeating the domain Yfby Y-periodicity,we get the whole fluid domain Df,and we can write it as
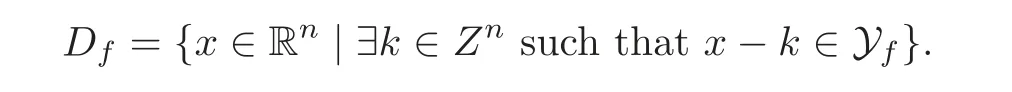
Then the solid part is defined by Ds=Rn−Df.It is easy to see that Dfis a connected domain,while Dsis formed by separated smooth subsets.In the sequel,we denote for all k∈Zn,Yk=Y+k and then Ykf=Yf+k.For all ε,we define the domain Ωεas the intersection of Ω with the fluid domain scaled by ε,namely,Ωε= Ω ∩ εDf.To get a smooth connected domain,we will not remove the solid part of the cells which intersect with the boundary of Ω.Now,the fluid domain can be also defined by
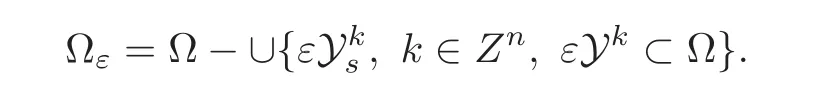
Throughout this paper,we denote by Lp(0,T;Lq(X))the time-space Lebesgue spaces,where X would be Ω or Ωε.Ws,p(X)will be the classical Sobolev space with all functions,whose all derivatives up to order s belong to Lpand Hs(X)=Ws,2(X).(X)is the subset of W1,p(X)with trace 0 on X.We also denote by W−s,p?(X)the dual space o(X),where p?is the conjugate exponent of p.C will be constants that may differ from one place to another.Throughout this paper,we will use?·?Xto denote the modules for all vectors or matrices if there is no confusion.
Due to the presence of the holes,the domain Ωεdepends on ε and hence to study the convergence of{uε,ρε,pε},we have to extend the functions defined in Ωεto the whole domain.This can be done in two different possible ways.
definition 2.1(see[10])For any fixed ϕ ∈ L1(Ωε),we define

as the null extension and
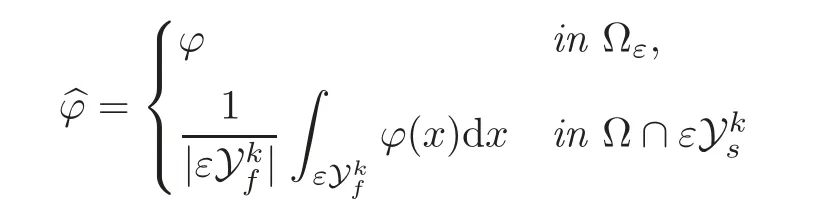
as the mean value extension.
The relation between the weak limits of both types of extensions is given by the following lemma.
Lemma 2.1(see[10]) For all ωε∈ Lp(Ωε), p ≥ 1,the following two assertions are equivalent:
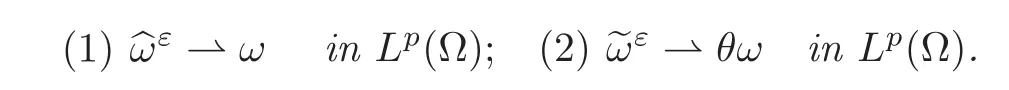
A very important property of the porous medium is a variant of the Poincaré’s inequality.Due to the presence of the holes in Ωε,the Poincaré’s inequality is given by the following lemma.
Lemma 2.2(see[11])Let 1≤p,q<∞and u∈(Ωε),then
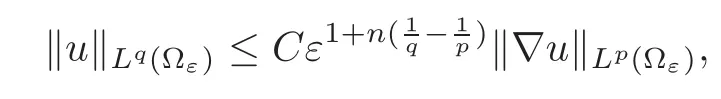
where C depends only on Yfand p,q satisfies
(1)1≤p (2)p≥n,p≤q<∞. Especially,if p=q,we have the standard inequality We introduce the restriction operator by the following lemma. Lemma 2.3(see[4])There exists an operator Rεwith the following properties: (1)Rεis a bounded linear operator on(Ω)ranging in(Ωε),p ≥ 2; (2)Rε[ϕ]= ϕ|Ωεprovides ϕ =0 in Ω − Ωε; (3)divxϕ =0 in Ω implies divxRε[ϕ]=0 in Ωε; (4)?Rε[ϕ]?Lp(Ωε)+ ε?∇Rε[ϕ]?Lp(Ωε) ≤ C(?ϕ?Lp(Ω)+ ε?∇ϕ?Lp(Ω)). In addition,we can find the restriction operator Rεsatisfies a compatibility relation with the extension operator introduced in definition 2.1,namely, Finally,we define the permeability matrix A.For 1 ≤ i≤ n,let(ωi,πi)∈ H1(Yf)×L2(Yf)/R be the unique solution of the following system: where ωi,πiare Y-periodic,eiis the standard basis of Rn.SetThen we get the cell problem whereare εY-periodic. Lemma 2.4(see[4,10])Letbe the solution to the cell problem and be extended to zero outside Ωε.Then the following estimates hold: for any 1≤q≤+∞,C only depends on q and Yf. Let us define The periodic lemma(see[1])shows that()jconverges weakly(or weakly?for p=+∞)to its average on εYfin Lp(Ωε)for 1 ≤ p ≤ +∞.It is easy to see that A is a symmetric positive defined matrix.The form of the permeability matrix has different form if Yshas different form.For more information about A,we refer the interested readers to[6]for detail. Now we introduce the definition of weak solution to the system(1.1)–(1.3). definition 2.2We shall say that a trio{uε,pε,wε}is a weak solution of(1.1)–(1.3),supplemented with the boundary and initial conditions(1.4)and(1.5)if and only if (1)uε∈ L∞(0,T;L2(Ωε))∩L2(0,T;H(Ωε)),and holds for any ϕ ∈([0,T)×)with divϕ =0.H(X)={u|u ∈(X),divu=0}. (2)wε∈ L∞(0,T;L2(Ωε))∩L2(Ωε×(0,T)),and the integral identity holds for any ψ ∈([0,T)×Ωε). The existence of weak solutions with finite energy is the following. Theorem 2.1(see[13])Under the above conditions and assumptions,for any fixed ε>0,there exists a global solution(uε,pε,wε)of the system(1.1)–(1.3)in the sense of definition 2.2. In this paper,we always assume that With all the preparation above,we are now in the position to state our main result in this paper. Theorem 2.2Let{uε,pε,wε}ε>0be a family of weak solutions to the system(1.1)–(1.3).We also assume that H is satisfied.Then,there exist three functions u,p,w such that where{u,p,w}satisfies the following homogenized system: where A is the so-called permeability matrix,which is defined by(2.1).Moreover,u,w satisfy the following initial conditions: and u|∂Ω=0 for any t∈ (0,T). Remark 2.1The relationship of u and∇p is often called the linear Darcy law.If we assume thatm(x,t)=M(x),we find that the degree of freedom w is determined only by M and κ for t is large enough. In this section,we collect all available bounds on the family{uε,pε,wε}.Let us begin with the basic estimates. In this subsection,we will obtain some estimates for the solutions to the system(1.1)–(1.3)which are independent of ε. Lemma 3.1Let{uε,wε}be the solution pair to(1.1)–(1.3).Under the conditions in Theorem 2.2,for ε∈ (0,1)small enough,the following estimates hold: where C does not depend on ε. Firstly,multiplying(1.2)by wεand integrating over Ωε×(0,t)for any t∈ [0,T],we have We have where C does not depend on ε. Secondly,multiplying the momentum equations by uεand integrating over Ωε× (0,t)for any t∈[0,T],we have By Lemma 2.2,the force term can be estimated by By Lemma 2.2 and(3.1),the last term can be estimated by for ε∈ (0,1)small enough. By the initial conditions,we immediately deduce where C does not depend on ε.By Lemma 2.2,we also have Note that Ωεwill vary as ε tends to 0+.We need to extend the unknowns uε,wεand pεto the whole domain Ω.It is reasonable to take null extensions for uεand wεsince the velocity on the solid part is 0.That is,we can define We will still denote the extensions by uεand wεif there are no confusions. The extension of the pressure pεis different from uεand wε.The reason is that the pressure on the solid part will not disappear even if the velocity is 0 on it.To give the extension on pε,we define a function in the following way: forRεis defined by Lemma 2.3. Now,we give estimates on the right-hand side.We only consider the case n=3 because n=2 is much easier. By Lemma 2.2,Lemma 2.3 and estimations in(3.2),we have To the third term,we have By using Lemmas 2.2–2.3 and(3.2)again,we have The last term is estimated by If we choose the test function ϕ such that divϕ =0,we have Thus,F,being orthogonal to divergence free functions,is the gradient of some functions ϑ.A result from[14]shows that up to a constant,we have At this moment,we can say that we have extended pεto the whole domain.We denote the extension function by Pε.It remains to determine the expression of Pεon the solid part.Suppressing the t dependence,following the steps in[15],we choose a smooth test function ϕ in(3.5),with compact support in one of the solid parts Ys,and we have Next,we choose a smooth test function in(3.5),with compact support in the entire cell Yf. Integrating by parts,we have In fact,we have proved the following lemma. Lemma 3.2The extension of pε,denoted by,has the form Moreover, In this section,we focus on the proof of Theorem 2.2.It contains three parts: (1)The convergence results in(2.3); (2)Recover the system(2.4); (3)Determine the initial and boundary conditions(2.5). Proof of Theorem 2.2Note that the velocity ε−2uεand the degree of freedom wεare both bounded in L2(Ω×(0,T)).By using the standard compactness theorem,we can extract subsequences,still denoted by itself,such that Due to(3.7),we can decomposeas following: wherei=1,2,···,6 is bounded uniformly in the corresponding space respectively.As above,we assume thatweakly in L2(Ω × (0,T))andweakly in the corresponding space respectively for i=2,3,···,6.LetWe have which implies Finally,by using the Nečas’s inequality(see[16–17]),we obtain p ∈ L2(0,T;H1(Ω))and In the sequel,we derive the homogenized model of(1.1)–(1.3).Note that Let We have which implies divu=0 in Ω×(0,T). Let ϕ ∈(Ω ×(0,T)).Takingas a test function in the momentum equations,whereis defined in Lemma 2.4 and has been extended 0 on∂Ω,we have Now we compute the limit of each term in above equality, By Lemma 2.2 and Lemma 2.4,we have To the last term,using Lemma 2.2 and Lemma 2.4,we have It is obvious that and as ε tends to zero. Finally,we consider the limit ofWe have Due to(3.2),we have as ε tends to zero. Integrating by parts in I1,we have Due to(3.3),we have By Lemma 2.4,we write I11in the following way: It is obvious and Combining(4.1)–(4.3),we obtain To pass the limit to(1.2),we take ϕ ∈(Ω×[0,T))as a test function and we have Note that Passing the limit,we obtain which implies that and w|t=0=w0(x). The expression of the degree of freedom in(4.6)can be written as where we assume that w vanishes on the boundary of Ω. At last,using the fact that ε−2uεis bounded in L2(Ω × (0,T))andis bounded in H−1(0,T;L2(Ω)),we conclude that ε−2uεis bounded in C([0,T];L2(Ω)).Then ε−2uεmake sense at t=0.Passing the limit,we have u|t=0=u0.For any t∈ (0,T),ε−1uεis bounded in(Ω).Then the trace of ε−2uεon ∂Ω makes sense.Passing the limit,we obtain u|∂Ω=0. Collecting all the information above,Theorem 2.2 is then proved. AcknowledgementsWe show our appreciations to the anonymous reviewers for their evaluating on this work.The authors also express their thanks to the editors for their sel fless help. [1]Sanchez-Palencia,E.,Nonhomogeneous media and vibration theory,Lecture Notes in Physics,Vol.127,Springer-Verlag,North Holland,Amsterdam,1979. [2]Keller,J.B.,Darcy’s law for flow in porous media and the two-space method,Nonlinear Partial differential Equations in Engineering and Applied Science,Proc.Conf.,Univ.Rhode Island,Kingston.RI,1979,Lect.Notes Pure Appl.Math.,Vol.54,Dekker,New York,1980,429–443. [3]Bensoussan,A.,Lions,J.L.and Papanicolaou,G.,Asymptotic analysis for periodic structures,Studies in Mathematics and Its Applications,Vol.5,Co.,Amsterdam,New York,North-Holland,1978. [4]Tartar,L.,Incompressible fluid flow in a porous medium convergence of the homogenization process,Appendix to Lecture Notes in Physics,Vol.127,Springer-Velag,Berlin,1980. [5]Allaire,G.,Homogenization of the Stokes flow in a connected porous medium,Asymptot.Anal.,2,1989,203–222. [6]Allaire,G.,Homogenization of the Navier-Stokes equations in open sets perforated with tiny holes I-II,Arch.Rat.Mech.Anal.,113,1991,209–259,261–298. [7]Allaire,G.,Homogenization of the Navier-Stokes equations with a slip boundary condition,Comm.Pure.Appl.Math.,44,1991,605–641. [8]Mikelic,A.,Homogenization of nonstationary Navier-Stokes equations in a domain with a grained boundary,Ann.Mat.Pura et.appl.,158(4),1991,167–179. [9]Mikelic,A.and Aganovic,I.,Homogenization of stationary of miscible fluids in a domain boundary,SIAM J.Math.Anal.,19,1988,287–294. [10]Masmoudi,N.,Homogenization of the compressible Navier-Stokes equations in a porous medium,ESIAM Control Optim.Calc.Var.,8,2002,885–906. [11]Zhao,H.and Zheng-An,Y.,Homogenization of the time discretized compressible Navier-Stokes system,Nonlinear Analysis,75,2012,2486–2498. [12]Brinkman,H.C.,A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles,Appl.Sci.Res.,A1,1947,27–34. [13]Lions,P.L.,Mathematical Topics in Fluid Mechanics,Vol.1,The Clarendon Press Oxford University Press,New York,1996. [14]Lipton,R.and Avellanda,M.,Darcy’s law for slow viscous flow past a stationary array of bubbles,Proc.Roy.Soc.Edinbergh Sect.A,114(1–2),1990,71–79. [15]Hornung,U.,Homogenization and porous media,Interdisciplinary Applied Mathematics Series,Springer-Verlag,New York,1997. [16]Temam,R.,Navier-Stokes Equations,North Holland,Amsterdam,1979. [17]Nečas,J.,Sur les normes équivalentes dans(Ω)et sur la coercivité des formes formellement positives,Séminaire Equations aux Dérivées partielles,les presses de l’Université de Montréal,1966,102–128.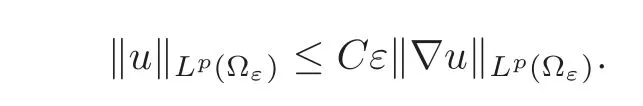
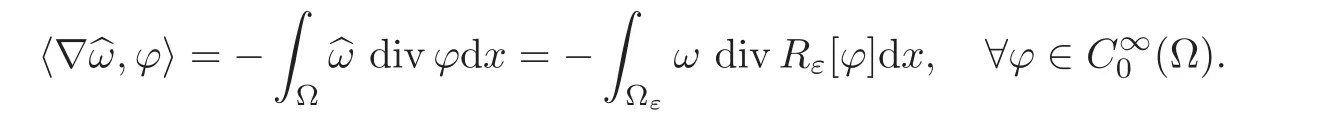
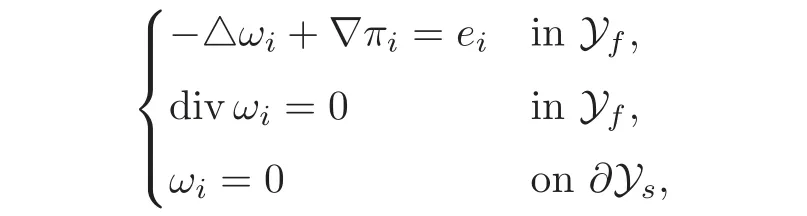
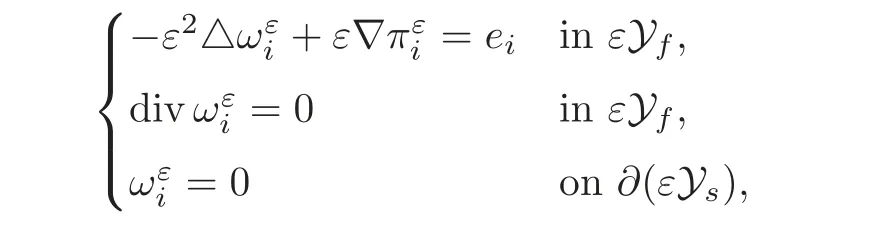
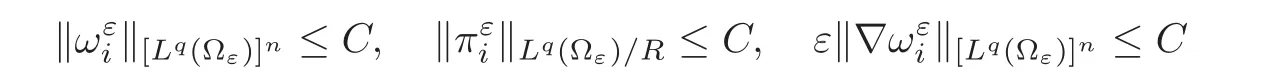
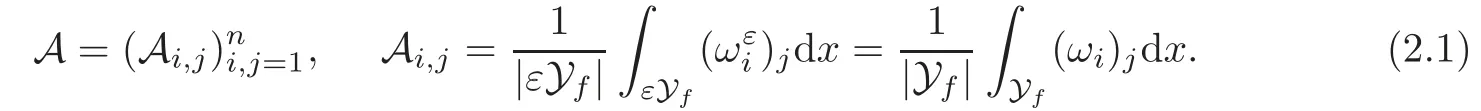
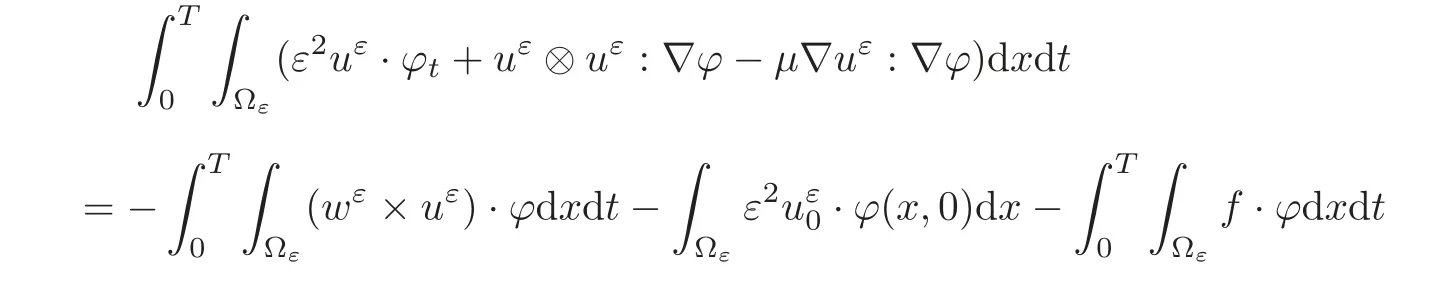
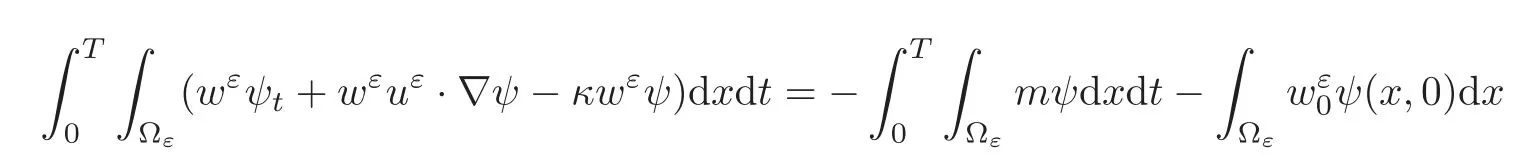
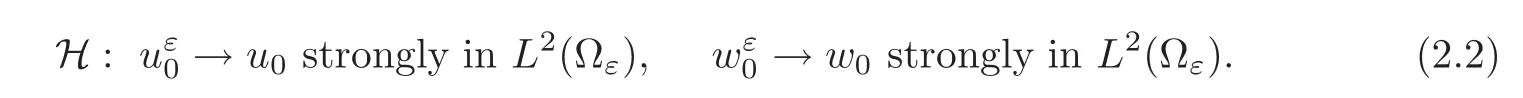
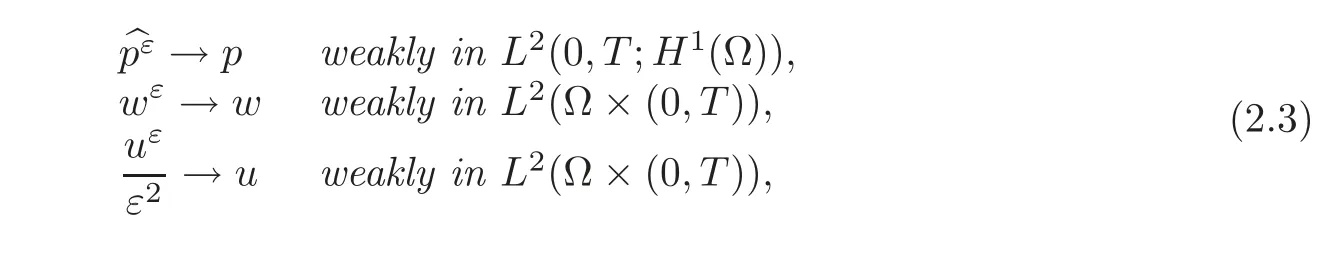
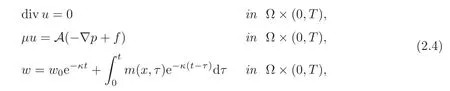
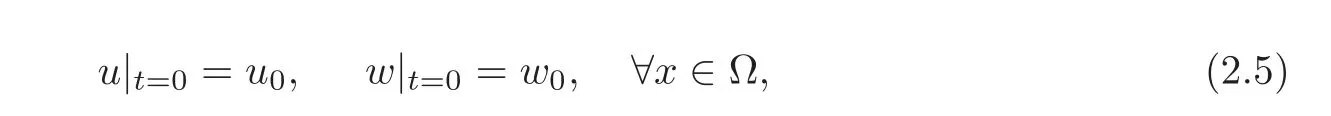
3 Uniform Bounds
3.1 Priori estimates for uεand wε
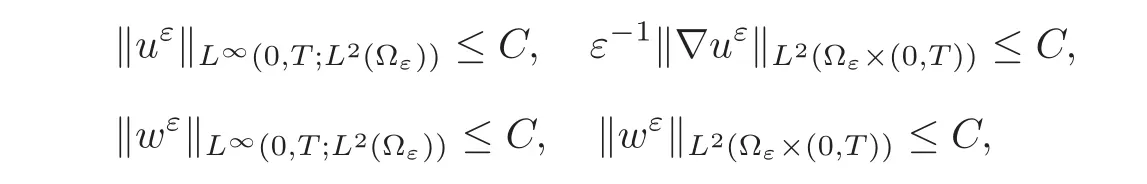
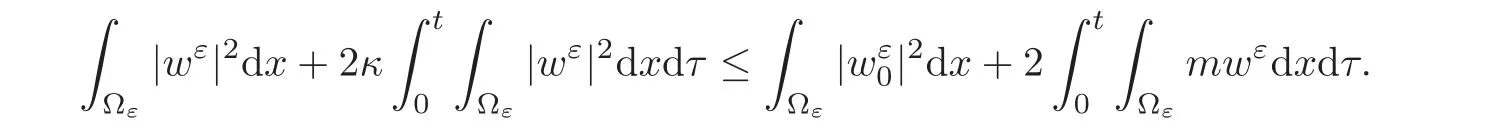
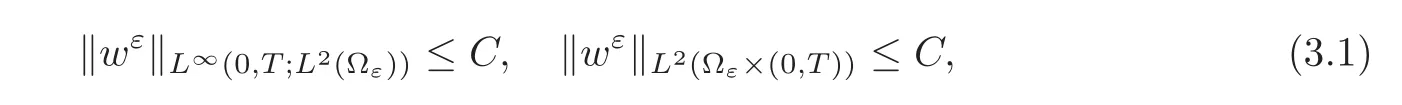
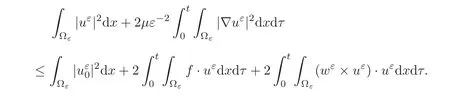
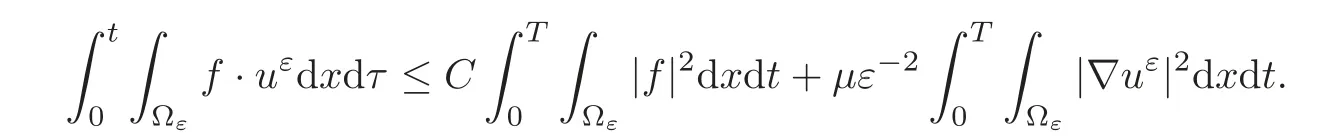
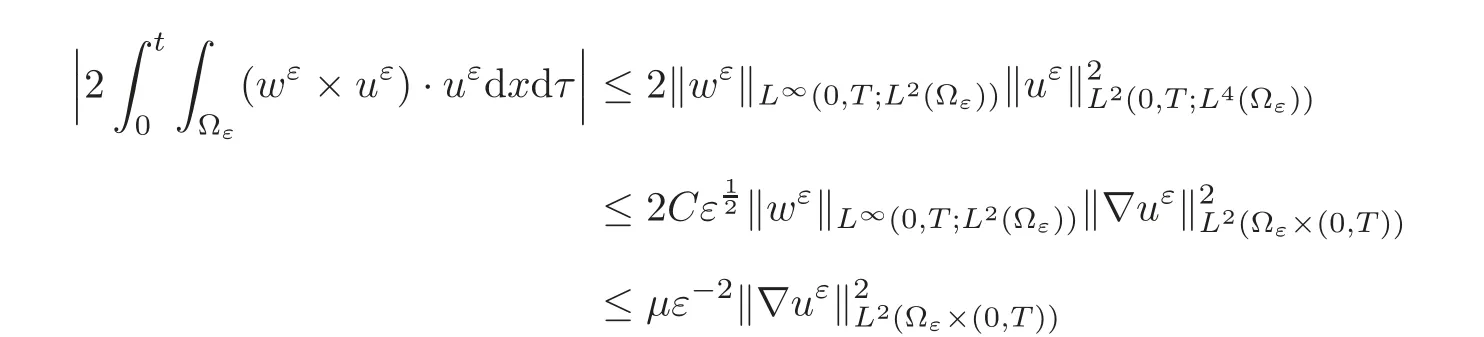
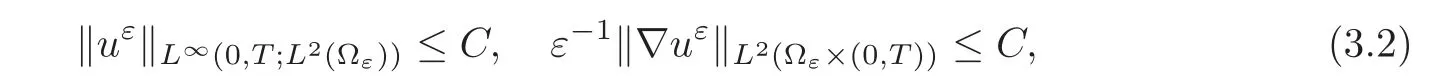

3.2 Extensions of uε,wε and pε

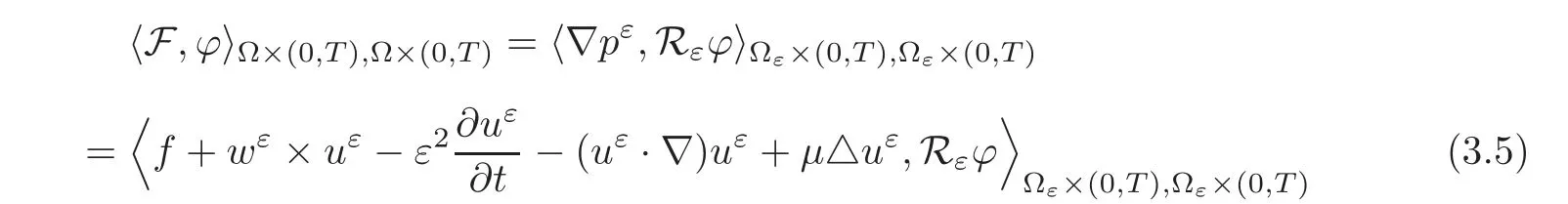
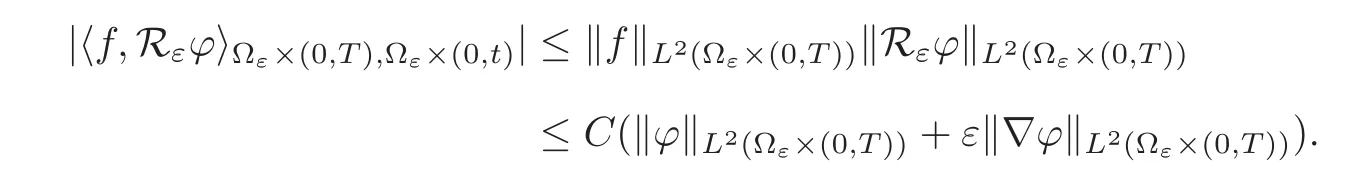
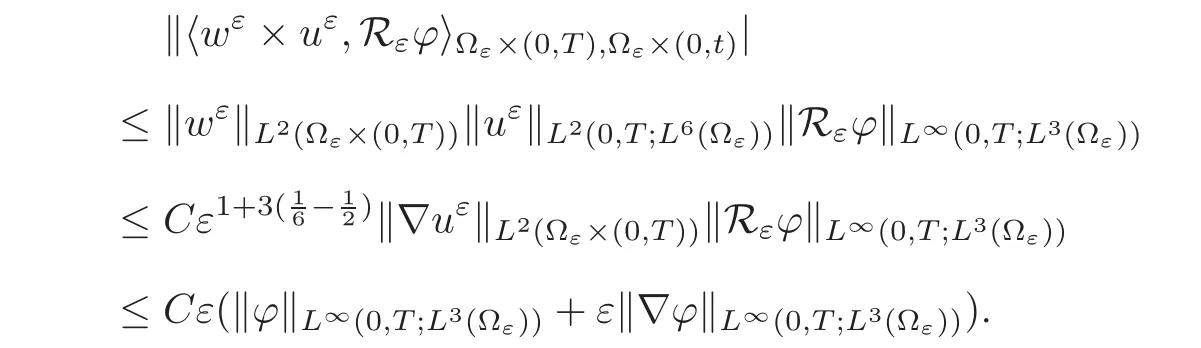
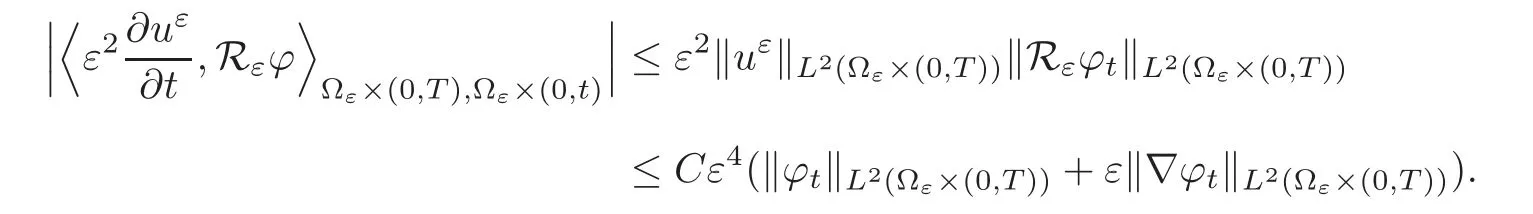
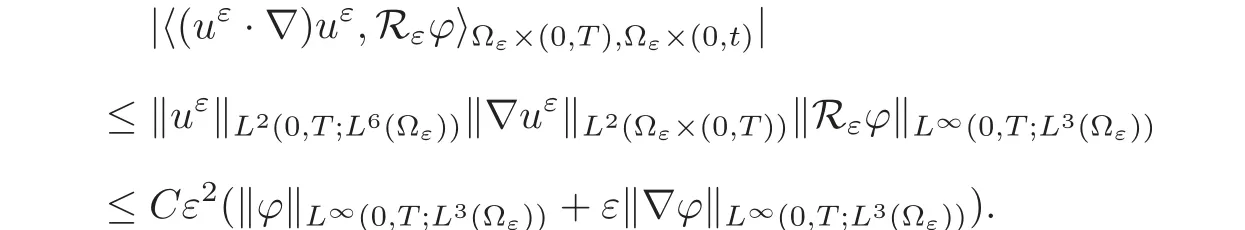
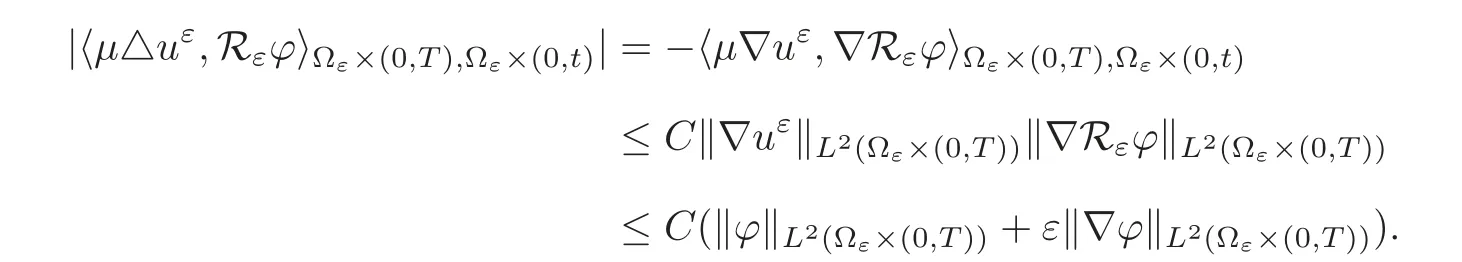
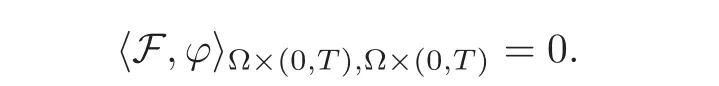
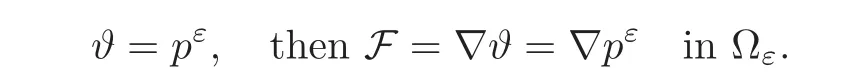
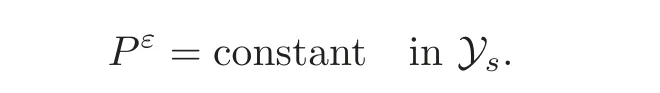
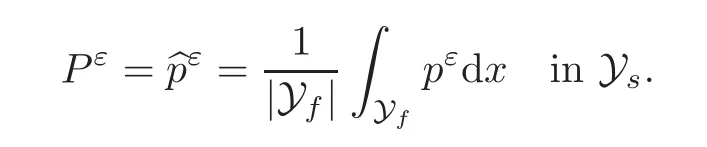
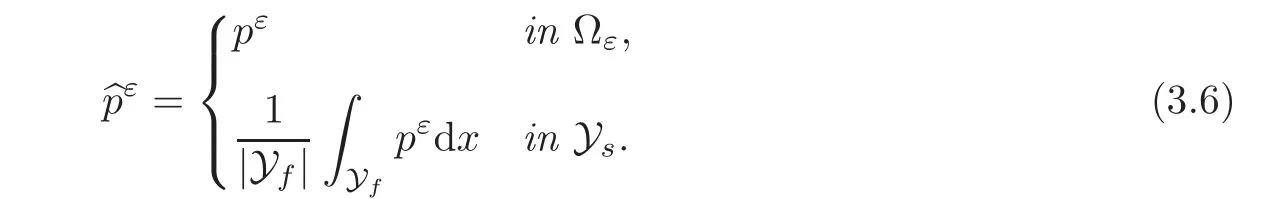

4 Proof of the Main Result
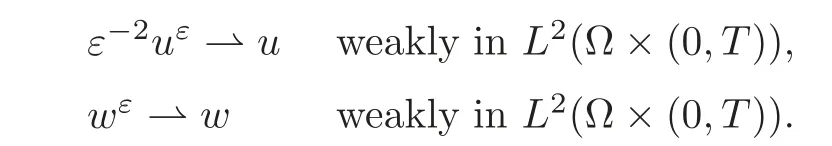
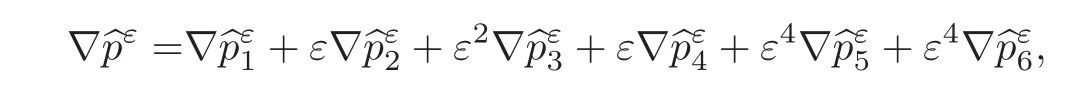
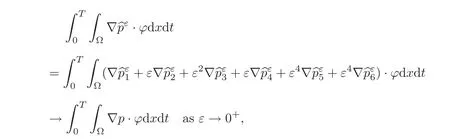
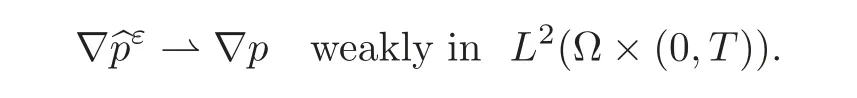

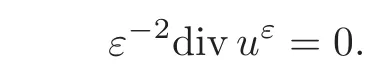

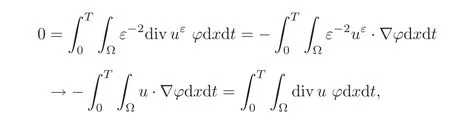

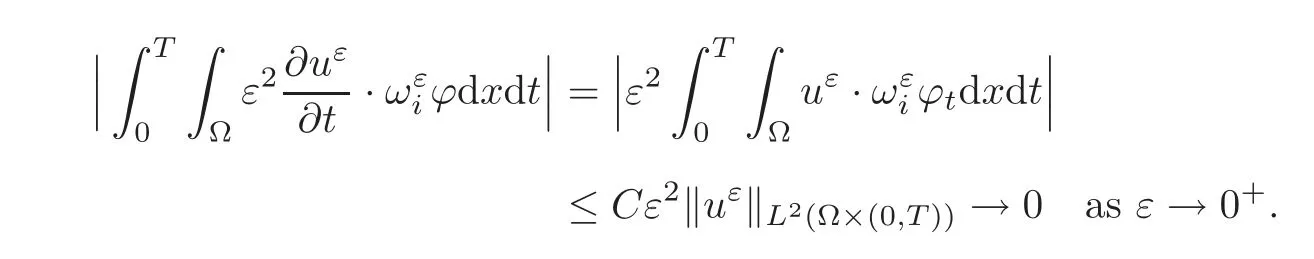
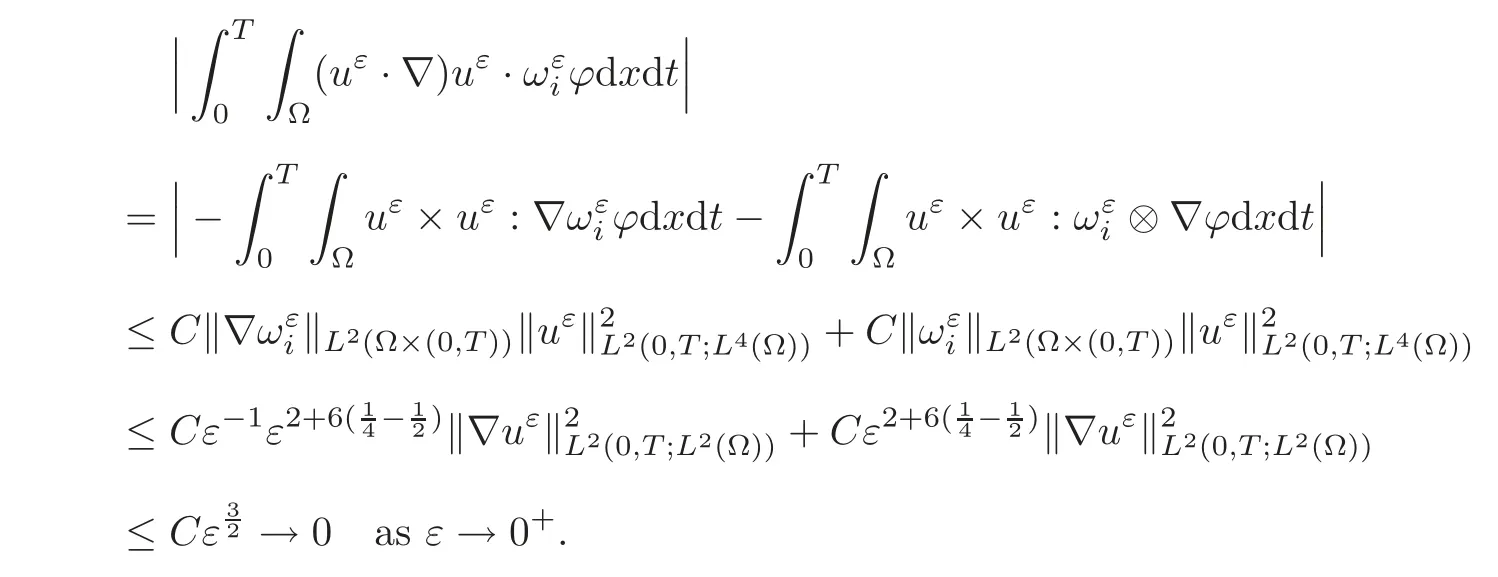

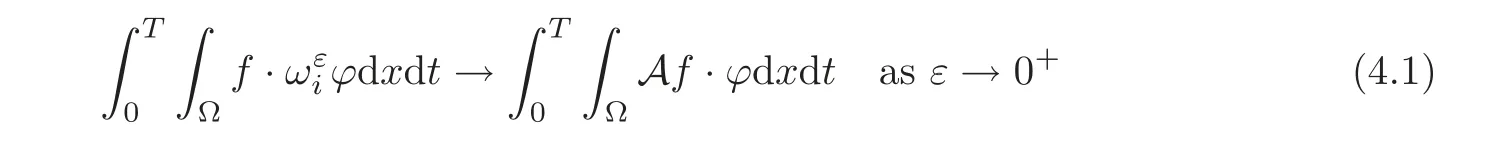
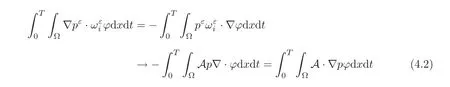
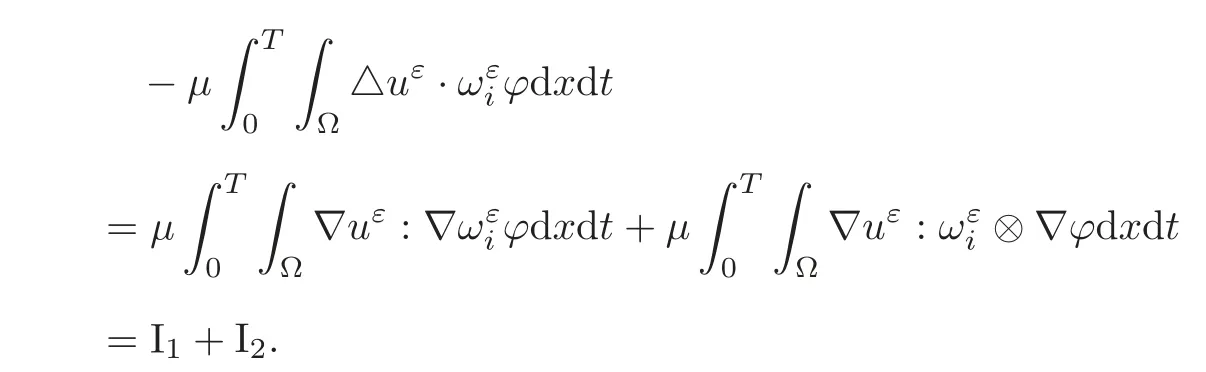
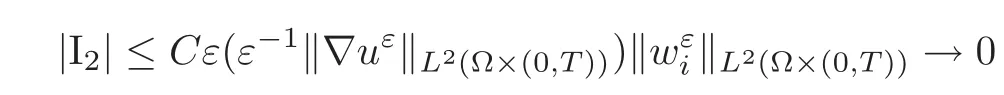
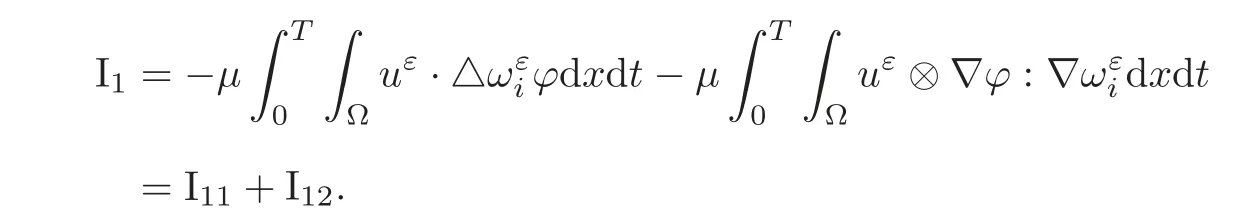
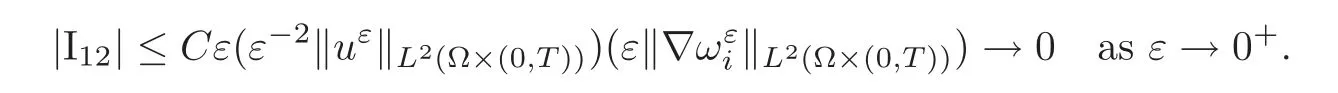
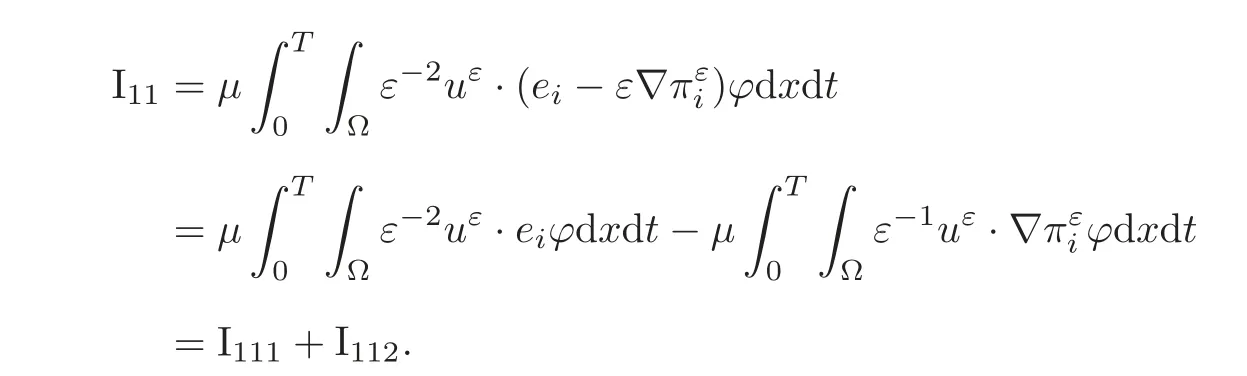

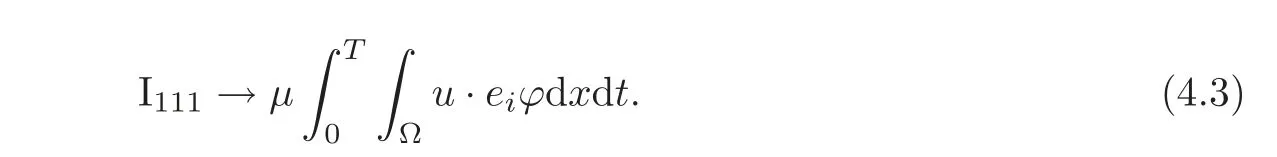

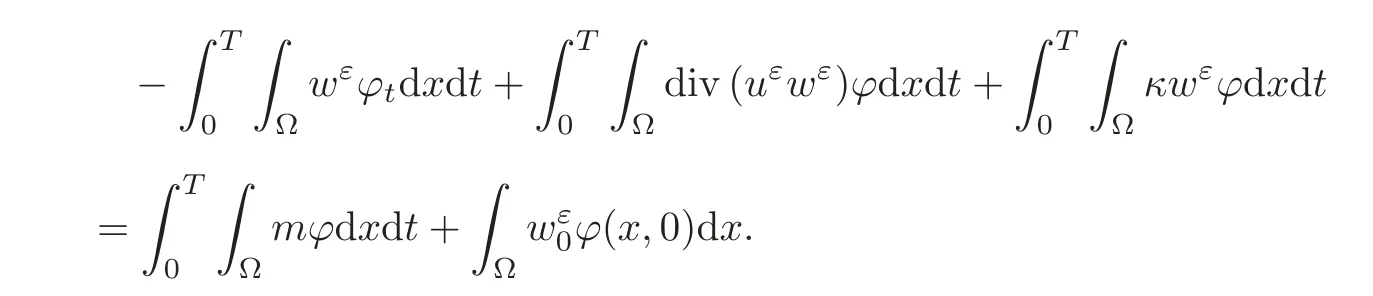
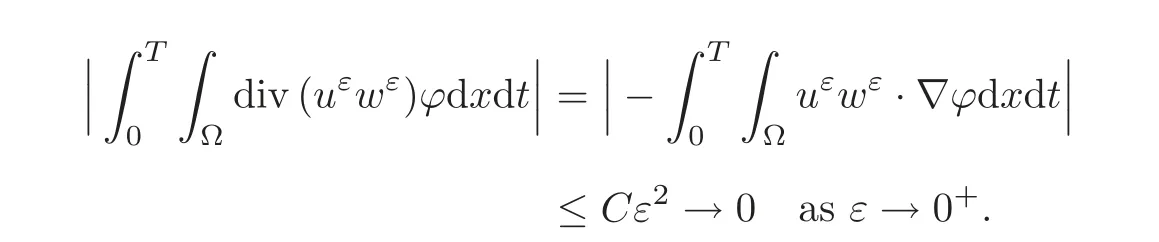

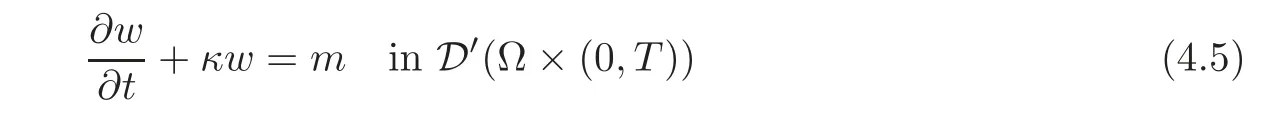
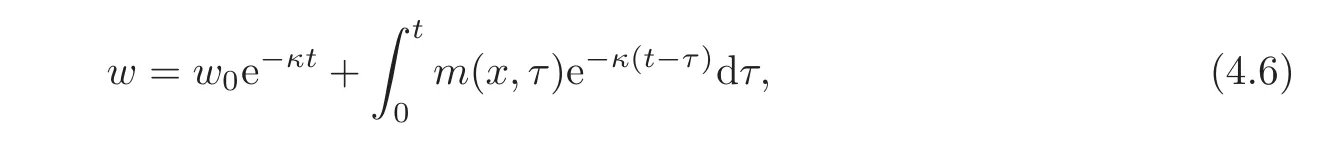
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Exact Boundary Observability for a Kind of Second-Order Quasilinear Hyperbolic Systems∗
- Rational Structure of X(N)over Q and Explicit Galois Action on CM Points∗
- Homogenization of Elliptic Problems with Quadratic Growth and Nonhomogenous Robin Conditions in Perforated Domains
- Modular Invariants and Singularity Indices of Hyperelliptic Fibrations
- New Quantum MDS Code from Constacyclic Codes∗
- On Robustness of Orbit Spaces for Partially Hyperbolic Endomorphisms∗
