Homogenization of Elliptic Problems with Quadratic Growth and Nonhomogenous Robin Conditions in Perforated Domains

Imen CHOURABIPatrizia DONATO

1 Introduction

In this paper,we study the homogenization of a class of a nonlinear elliptic problems containing a nonlinear term depending on the solution uεand on its gradient∇uεwith quadratic growth.The problem is posed in the perforated domain= ΩTεobtained by removing from an open bounded set Ω of RN(N ≥ 2)a closed set Tεrepresenting a set of ε-periodic holes of size ε.We prescribe a Dirichlet condition on the exterior boundaryand a nonhomogeneous nonlinear Robin condition on the boundaryof the holes.More precisely,we study the asymptotic behavior,as ε tends to zero,of the bounded solution uεof the following problem:

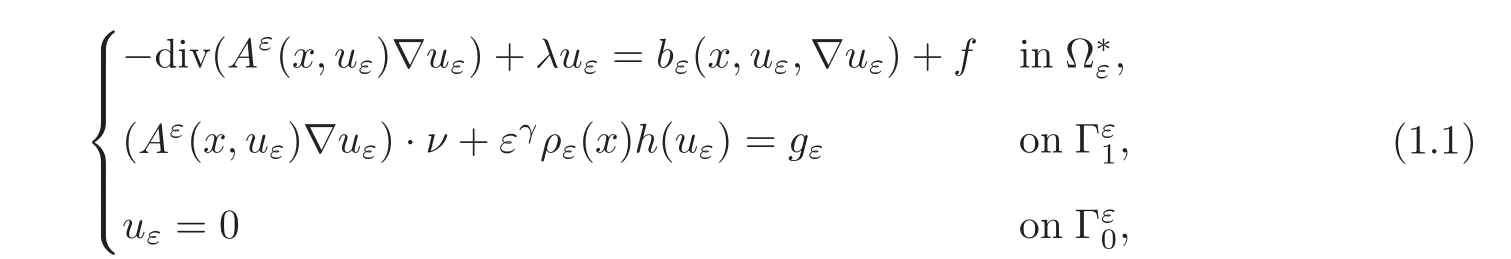
where λ ≥ 0 and ν is the unit external normal vector with respect to

The function f belongs to Lm(Ω)with m>and ρ(x)= ρ??,where ρ is a Y-periodic function that belongs to L∞(∂T),Y and T being the reference cell and the reference hole,respectively.

We assume thatis a bounded,uniformly elliptic,Y-periodic matrix field and that the function bε(x,t,ξ)is a Carathéodory function on Ω × R × RNwith quadratic growth with respect to the third variable.

We also suppose that gεis defined by

where g is a Y-periodic function in Lr(∂T)with r>N − 1 and M∂T(g)denotes its mean over∂T.

Let us mention that this type of equations appears in calculus of variations and stochastic control and the nonlinear term b(y,t,ξ)appears in the Euler equation of certain functionals.

The homogenization of this kind of equation with a linear matrix field Aε(x)involving a term bε(x,t,ξ)continuous in x variables and with quadratic growth with respect to ξ has been studied in[4–5]for a fixed domain and in[19]for perforated domains with Neumann boundary condition and f=0.In[20]the case where bε(x,t,ξ)is singular in t in a fixed domain has been studied.

The homogenization result of problem(1.1)is stated in Theorem 2.1.The main feature of this result is that the expression of the limit nonlinearity b0depends on the average of the nonhomogeneous boundary function g.This is due to the fact that,as proved in[10],the corrector results for the associated linear problem are different in the two cases M∂T(g)0 and M∂T(g)=0.

More precisely,according to these two cases,we derive two different limit problems for the L2-limit u0of the zero extension of uε:

(1)If M∂T(g)0 or g≡ 0,the function u0is a solution of the problem

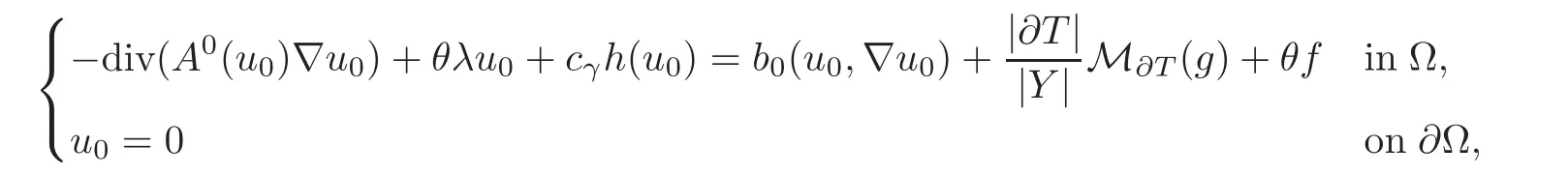
where θ=and A0(t)is the homogenized matrix introduced in[1](see also[2–3,8])for quasilinear problems with Neumann conditions in perforated domains and the constant cγis defined by

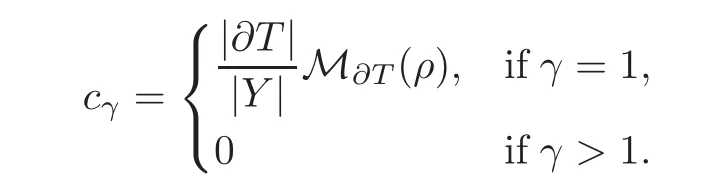
The function b0is given by

where{Cε(·,s)}is the usual corrector.

(2)If M∂T(g)=0(with g?0)and A is independent of t,i.e.,A(y,t)=A(y)in Y,the function u0is a solution of the problem

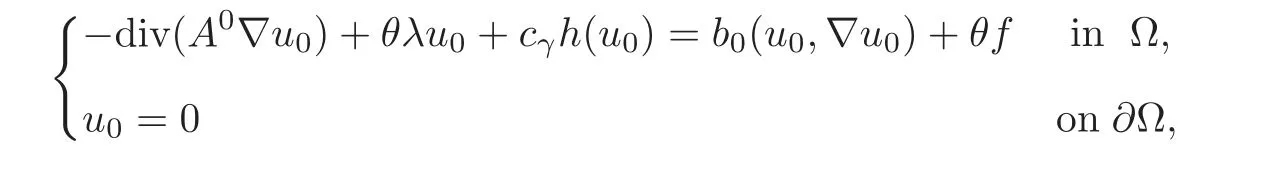
where A0is the now classical constant homogenized matrix introduced in[18].The function b0is defined by

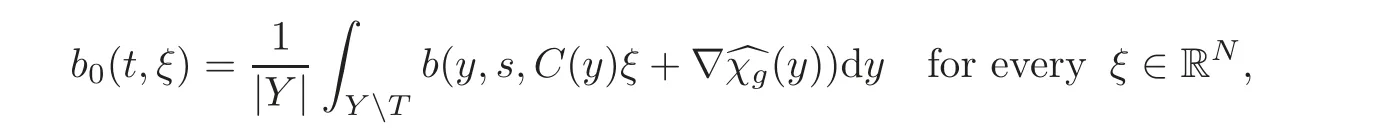
where Cεis the usual corrector(independent of t)and the functionis the solution of the related problem posed in the reference cell with a nonhomogeneous Neumann data g.

As in[4–5,19–20],the main tool in the homogenization process is a corrector result.To do that,we construct a suitable associated linear problem.The homogenization and the corrector results for this linear problem have been already proved in[10].We use here the result about correctorsproved therein and we show that the corrector for the linear problem is also a corrector for our nonlinear problem in both cases M∂T(g)?0 and M∂T(g)=0.

Here,the main difficulty in particular,when passing to the limit in the nonlinear problem,is due to the presence of the holes,and the solutions converge neither strongly in L2(Ω)nor almost everywhere in Ω.To overcome this difficulty,we do not use the extension operators as done in[19]for the case of homogeneous Neumann condition.We apply here the periodic unfolding method introduced in[12](see[13]for more details)and extended to perforated domains in[16–17](see also[11]for more general situations).Using the fact that the unfolding operatorfor perforated domains transforms any function defined oninto a function defined on a fixed domain,we prove a new technical convergence result involving nonlinear functions,stated in Theorem 4.1,which provides suitable weak convergence results.This technical tool allows to pass to the limit and to prove the corrector result simplifying the proofs and the presentation,even in the case studied in[19].

This paper is organized as follows:In Section 2 we present the problem and state the main results.In Section 3 we recall some preliminary results.Section 4 is devoted to the proof of the homogenization result.

2 Position of the Problem and Statement of the Main Results

In order to state the main results of this paper,we recall some general notations introduced in[11](see also[12]for the unfolding periodic method in perforated domains).

We denote by

Ω an open bounded set of RN(N ≥2)with∂Ω being Lipschitz continuous;

Y=]0,l1[× ···×]0,lN[the reference cell,where li>0 for all 1 ≤ i≤ N;

T,the reference hole,a compact set contained in Y and Y∗=YT the perforated reference cell,with∂T Lipschitz-continuous with a finite number of connected components;

Tε=the closed set of RNrepresenting the holes,where

G=where b=(b1,···,bN)is a basis in RN;

= ΩTεthe perforated domain;

=interiorandthe corresponding perforated set;

Λε=and=the corresponding perforated set.

As in[8,17],we decompose(see Figure 1)the boundary of the perforated domainas follows:

In the sequel,we also denote by

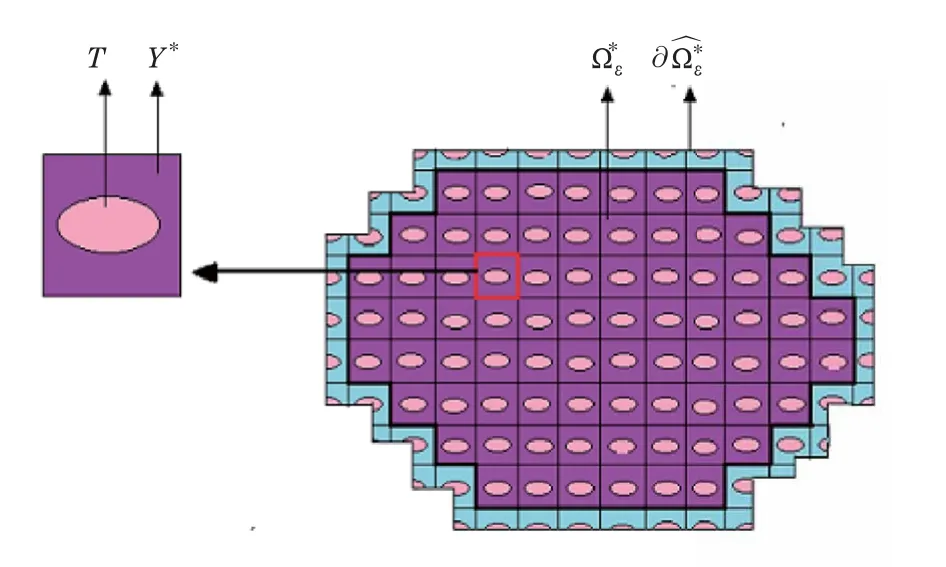
Figure 1 The perforated domainand the reference cell Y

χEthe characteristic function of a subset E of RN;

|E|the Lebesgue measure of a Lebesgue-measurable subset E of RNand|∂E|the(N − 1)-Hausdor ffmeasure in RNof its boundary∂E;

MY∗(v)=v(y)dy the average of any function v∈L1(Y∗);

M∂T(v)=v(y)dσythe average of any function v ∈ L1(∂T);

or(v)∼the extension by zero on Ω of any function defined on;

ν the unit external normal vector with respect to YT or;

M(α,β,Ω)the set of matrix fields A=(aij)1≤i,j≤N∈ (L∞(Ω))such that

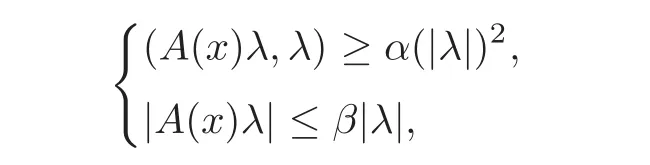
for x a.e in Ω,any λ ∈ RNand α,β ∈ R,with 0< α < β;

θ=the proportion of material;

c different strictly positive constants independent of ε.

Let us recall that

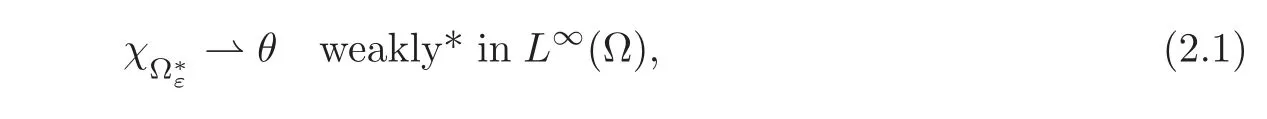
as ε tends to zero.

Our purpose is to study the asymptotic behavior,as ε tends to zero,of the following problem:

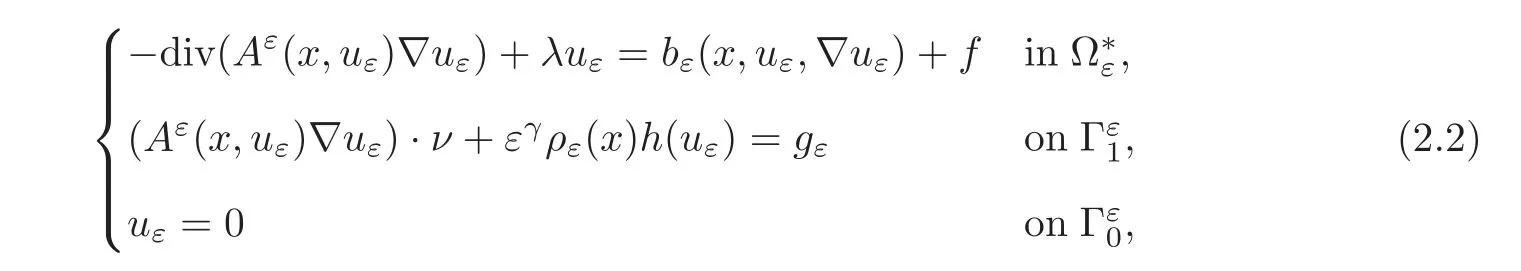
where we suppose that

(H1)λ≥0.

(H2)0 ≤ f ∈ Lm(Ω)with m>,f?0.

(H3)The real matrix field A:(y,t) ∈ Y ×R?−→ A(y,t)={aij(y,t)}i,j=1,···,N∈ RN2satisfies the following conditions:

(H4)The function h is an increasing and continuously differentiable function such that for some positive constant C and an exponent q,one has

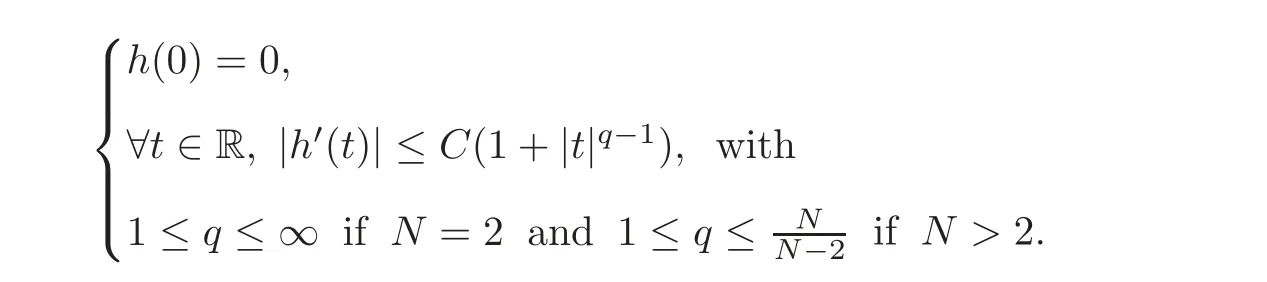
(H5)The function ρ is positive and Y-periodic,and it belongs to L∞(∂T).

(H6)The function g is Y-periodic and belongs to Ls(∂T),where s>N − 1.

(H7)The function b:(y,t,ξ) ∈ Y × R × RN?−→ b(y,t,ξ) ∈ R satisfies the following conditions:

For almost every x in Ω,every t in R and every ξ in RN,we set

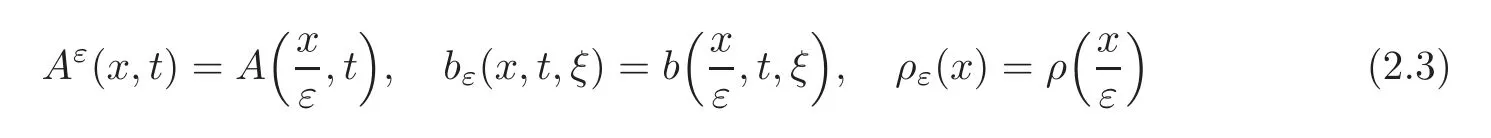
and

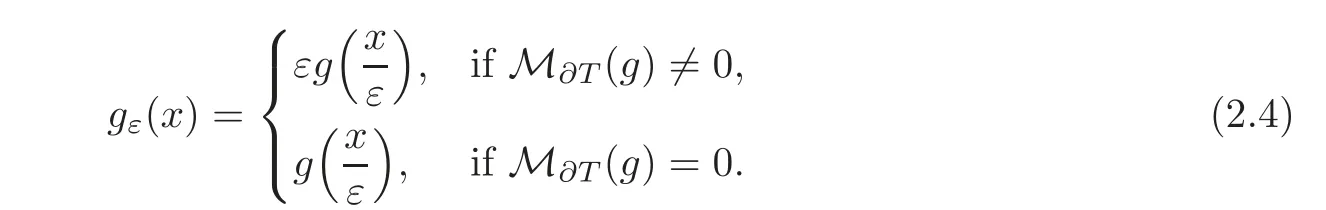
We introduce now the space

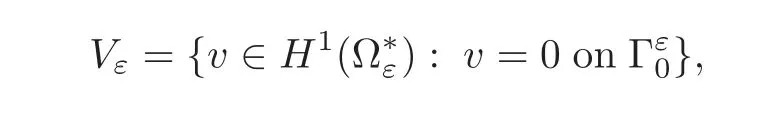
equipped with the norm

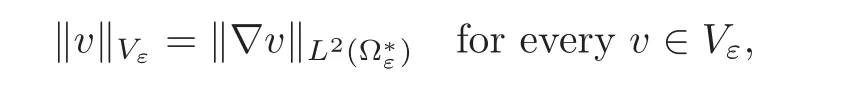
and the variational formulation of problem(2.2)

The existence of a solution to problem(2.5),under the assumptions(H1)–(H7),has been proved in[9,Theorem 6.1]together with the boundedness of the solution and some uniform estimates for the sequence{uε}ε.More precisely,it was proved that there exists a constant c such that

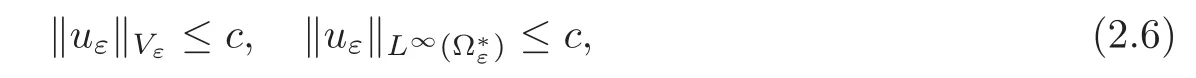
where c is independent of ε and depends only on α,m,s and the Sobolev embedding constant,with the numbers α,m and s being defined by(H2)–(H3)and(H6),respectively.

We recall that(see[1–2,8,10])for every fixed t ∈ R,the homogenized matrix A0(t)is defined by

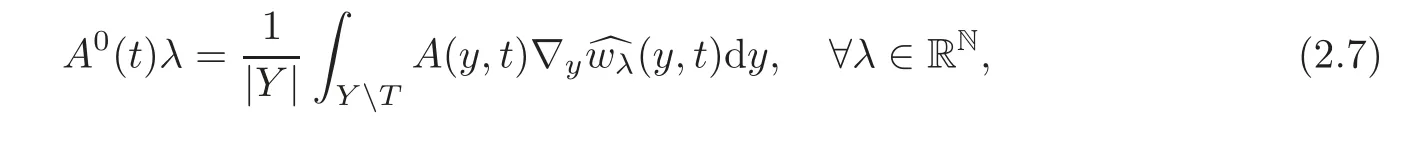
where

and for every t∈R and λ ∈RN,the function(·,t)is the solution to the problem

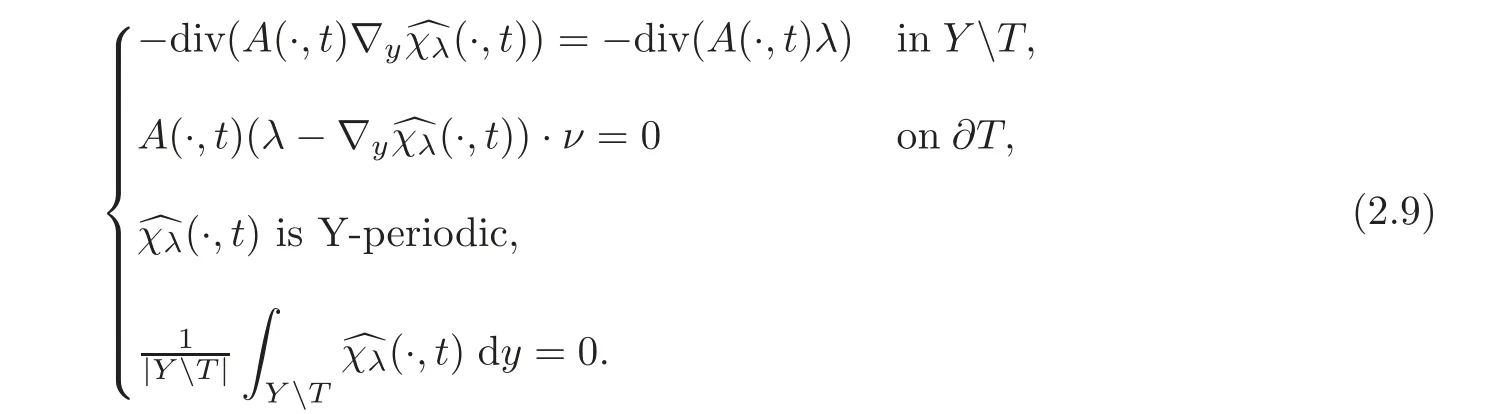
We also define for any ε and every fixed t∈ R,the corrector matrix Cε(·,t)=given by(see[10])

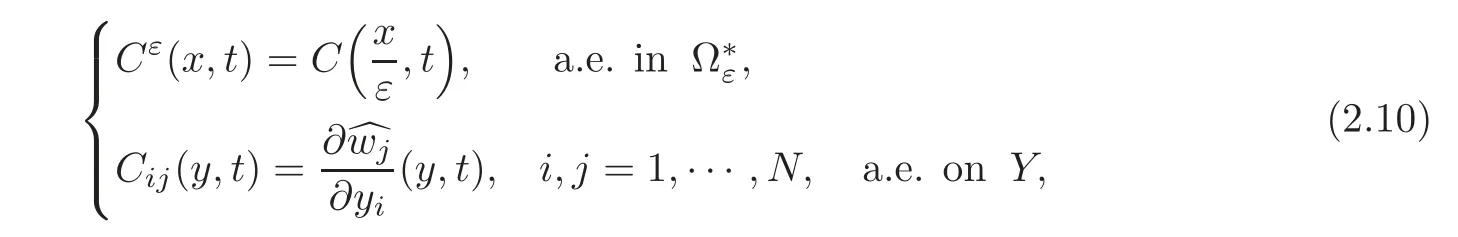
whereis the canonical basis of RN.

We recall below its main properties.

Proposition 2.1(see[10])Under the assumption(H3),let uεbe the solution of problem(2.2).Then,there exists a constant c1,independent of ε,such that for some r>2,

Moreover,the functions Cε(·,uε)are equi-integrable and

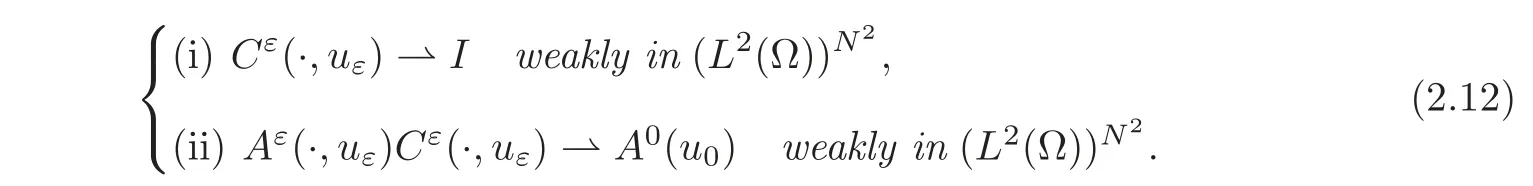
We can now state the main result of this paper.

Theorem 2.1Under the assumptions(H1)–(H7),let uεbe the solution of problem(2.2).

Then,there exists a subsequence{uε}(still denoted by ε),a function u0∈(Ω)∩ L∞(Ω)and a Carathéodory function b0:R × RN→ R such that

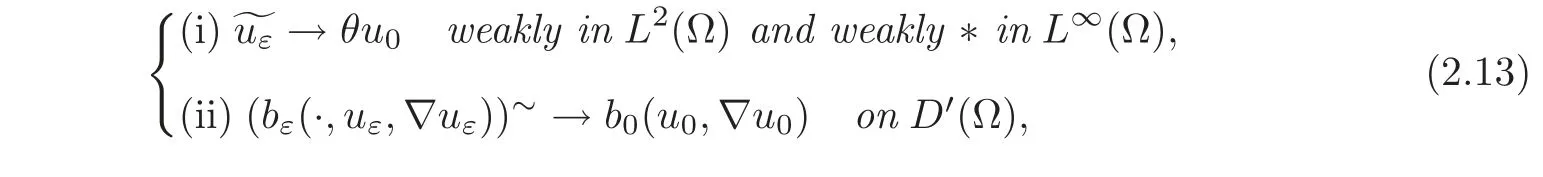
where θ is defined by(2.1).

The homogenized problems,depending on the mean of g,are the following ones:

(1)If M∂T(g)0 or g≡0,the function u0is a solution of the problem

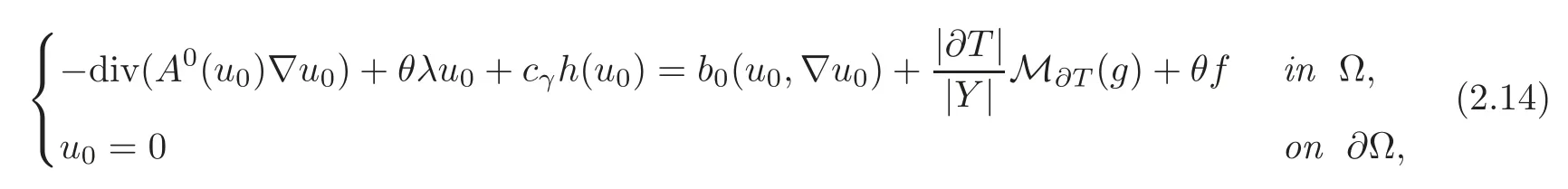
where the homogenized matrix A0(t)is given by(2.7)for every fixed t∈ R,and the constant cγis defined by

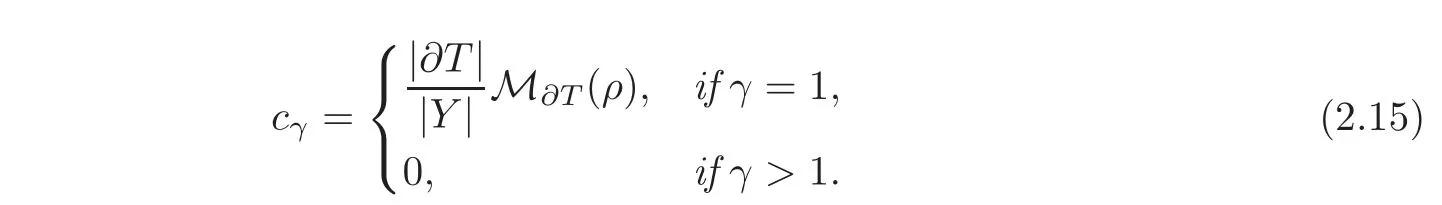
The function b0is given by

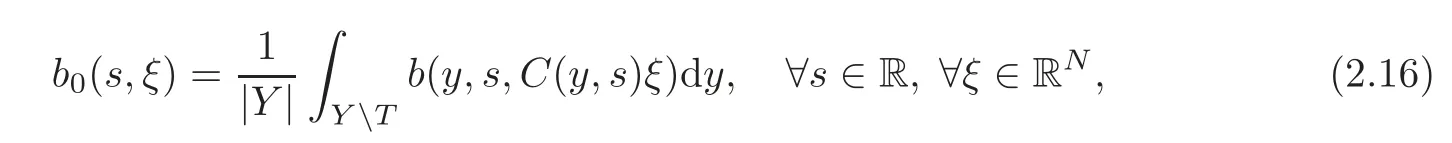
where the corrector matrix fields{Cε(·,s)}are defined by(2.10).Moreover,

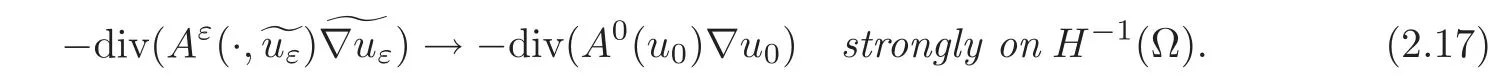
(2)If M∂T(g)=0(with g?0)and A is independent of t,i.e.,A(y,t)=A(y)in Y,the function u0is a solution of the problem

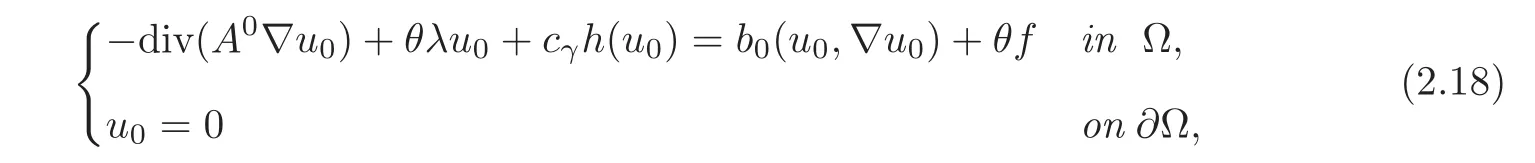
where the constant homogenized matrix A0is given by(2.7)(independent of t).

The function b0is defined by

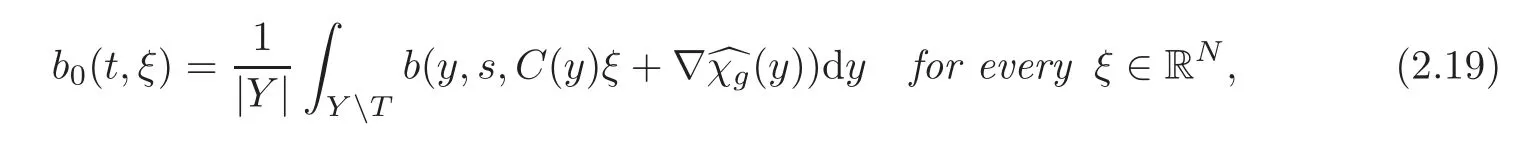
where Cε(·)is defined by(2.10)(independent of t)and the functionis the solution of the following problem:

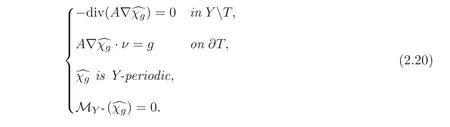
Moreover,

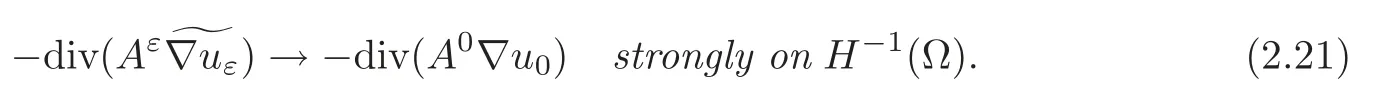
This result will be proved in Section 4.

Remark 2.1Let us point out the main novelty in this result.It concerns the fact that the presence of gεin the nonhomogeneus boundary condition of problem(2.2)gives rise to two different limit nonlinearities b0in the problem,according to the case M∂T(g)0 or M∂T(g)=0.

This is due to the fact that the corrector results for the associated linear problem are different in the two cases,as recalled in Theorem 3.2.

We end this section by stating the following result,which shows that Cεis a corrector for the nonlinear problem(2.5).

Corollary 2.1Under the assumptions of Theorem 2.1 and the notation therein,we have the following assertions:

(1)If M∂T(g)0 or g=0,then

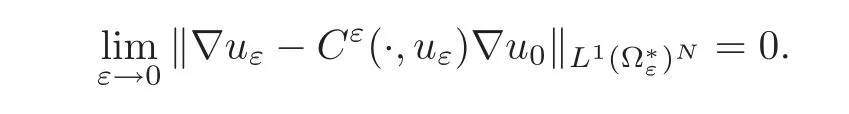
(2)If M∂T(g)=0 and A is independent of t,i.e.,A(y,t)=A(t)in Y,then

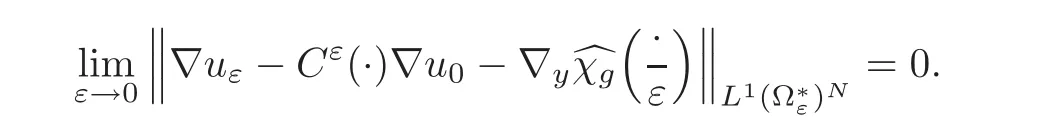
ProofThis corollary is a straightforward consequence of Theorem 3.4 and Theorem 4.1 proved in Sections 3 and 4,respectively.

3 Some Preliminary Results

In this section,we recall some homogenization and corrector results proved in[10].

To do that,we introduce as in[10]a linear operator Lεfrom H−1(Ω)to(Vε)?verifying the following assumption:

(H8)If{ψε}is a sequence such that

then

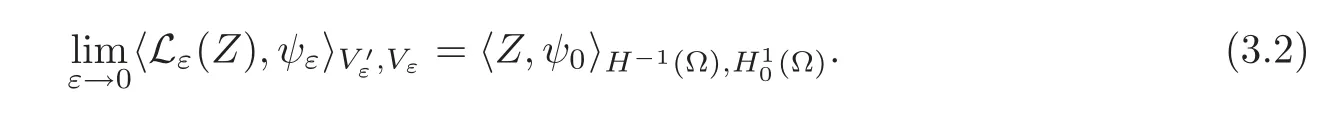
Remark 3.1Let us point out that there exist many operators Lεverifying the assumption(H8),which can be constructed in different ways.

For instance,the assumption(H8)is satisfied for Lε=(see Remark 4.3 of[10]),whereis the adjoint of the linear extension operators Pεintroduced by Cioranescu D.and Saint Jean Paulin J.in[18].Let us recall that for any sequence{vε}εin Vε,we have that

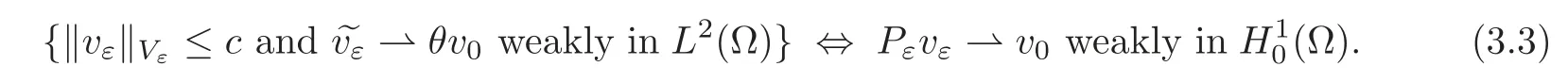
Another(different)operator can be defined by using the periodic unfolding method as done in[21]when studying the correctors for the wave equation in perforated domains via the above method.We refer to[10,Remark 2.3]for more details and comments.

We recall first the following homogenization result.

Theorem 3.1(see[10]) Under the assumptions(H1)–(H6)and(H8),let Z be given in H−1(Ω)and let vεbe the unique solution of problem

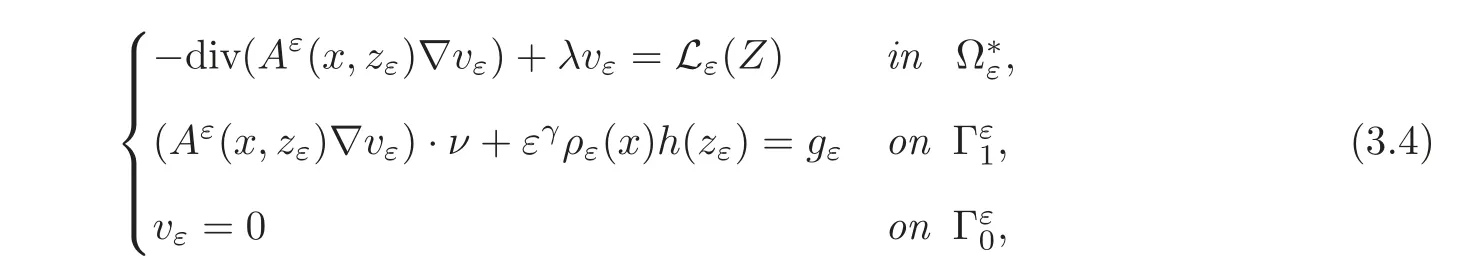
where the sequence{zε}εbelongs to Vεand Aε,ρεand gεare given by(2.3)and(2.4).

Suppose that the sequence{zε}εsatisfies(3.1),that is

with z0∈(Ω)and θ given by(2.1).Then,as ε tends to 0,we have the following convergences:

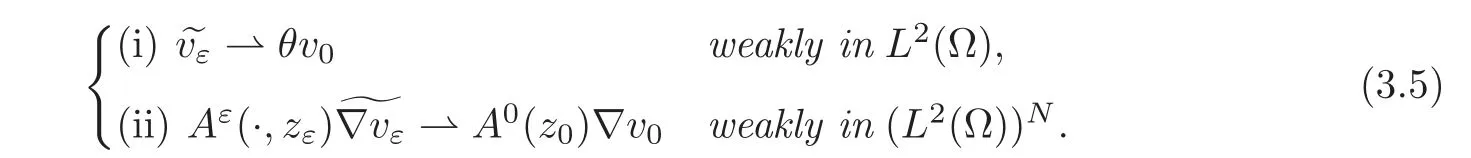
The function v0is the unique solution of the problem

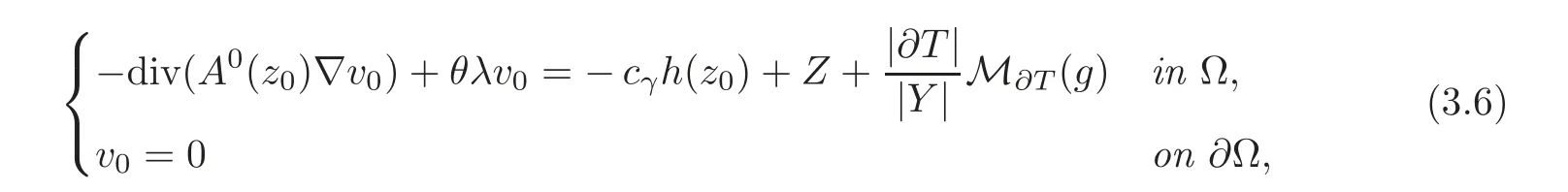
where the homogenized matrix A0(t)and the constant cγare defined by(2.7)and(2.15)respectively.

Let us recall now the results concerning the convergence of the energies and the corrector,proved in[10]where we distinguish the two cases given in(2.4).

Theorem 3.2(see[10])Under the assumptions of Theorem 3.1,let A0be defined by(2.7)anddefined by(2.20).Let vεand v0be the solutions of problems(3.6)and(3.4),respectively.

(1)If M∂T(g)?0 or g≡0,then

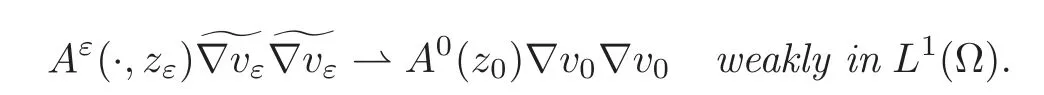
Moreover,if{Cε(·,zε)}is defined by(2.10),we have

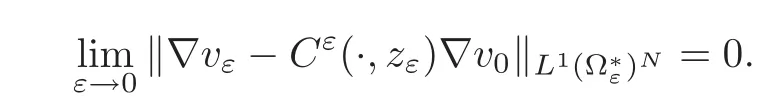
(2)If M∂T(g)=0(with g0)and A is independent of t,i.e.,A(y,t)=A(y)in Y,then

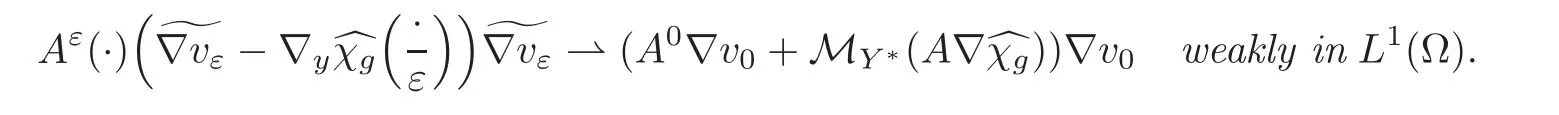
Moreover,if Cε(·)is defined by(2.10)(independent of t),we have

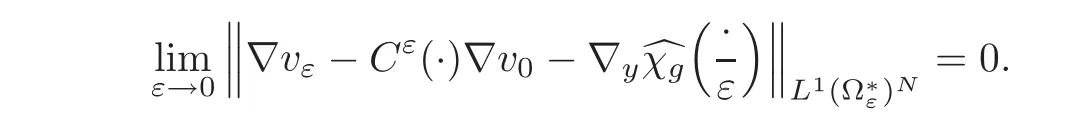
The proof of the corrector result given in[10]is based on the proposition below,which will be needed in the sequel.

Proposition 3.1(see[10])Under the assumptions of Theorem 3.1 and with the notations therein,we have the following assertions:

(1)If M∂T(g)0 or g≡0,then

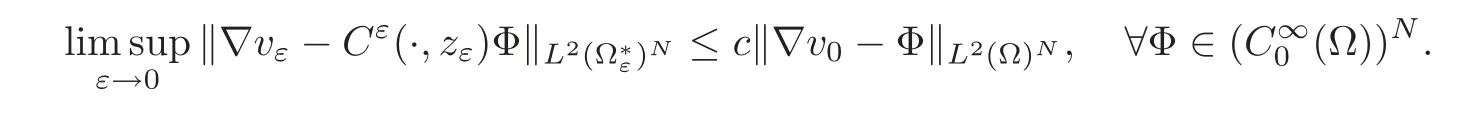
(2)If M∂T(g)=0(with g0)and A is independent of t,i.e.,A(y,t)=A(t)in Y,then

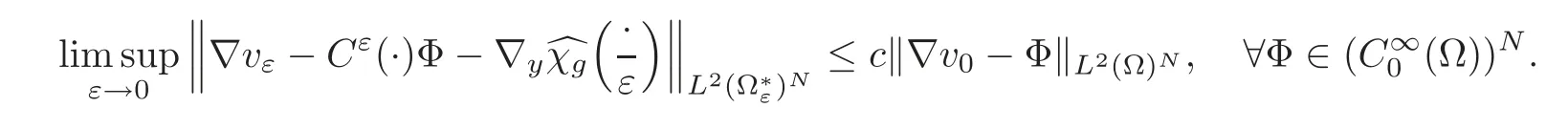
In both cases,c=C(α,β)is a constant independent of Φ.

We also recall the following property.

Lemma 3.1(see[5])Let{gε}εbe a sequence of functions which converges weakly in L1(Ω)to a function g0and let{tε}εbe a sequence of equibounded and measurable functions,which converges almost pointwise in Ω to a function t0.Then

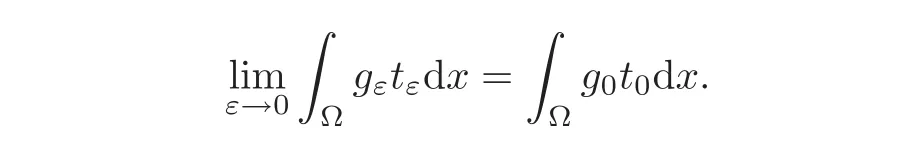
We end this section by stating the following result.

Proposition 3.2Under assumption(H7),let{bε}εbe the sequence of the Carathéodory functions given by(2.3).Then,the function b0given by(2.16)or(2.19)satisfies(H7)and for any φ in((Ω))Nand ϕ0in L∞(Ω),one has the following assertions:

(1)If M∂T(g)=0 or g=0,then

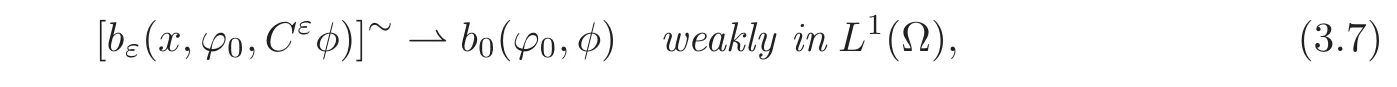
where{Cε(·,zε)}is defined by(2.10).

(2)If M∂T(g)=0 and A is independent of t,i.e.,A(y,t)=A(y)in Y,

where Cε(·)is defined by(2.10)(independent of t)and the functionis the solution of problem(2.20).

ProofThe convergence(3.7)is a simple consequence of Theorem 2.6 of[19](see also[5]for the case of a fixed domain)and the convergence(3.8)can be deduced by the same arguments as those used to prove(3.7).

4 Proof of the Main Result

4.1 A technical result

In this section,we give a preliminary tool which will play an essential role in proving the corrector result stated in Theorem 4.2,and seems interesting by itself.

To prove it,we use the periodic unfolding method,introduced in[12](see[13]for a general presentation and detailed proofs)and extended to perforated domains in[16–17](see[11]for more general situations and a comprehensive presentation).

Theorem 4.1Let{ψε}be a sequence satisfying(3.1).

(1)The following convergences hold:

(2)Let p ∈ [1,+∞)and{hε}be a sequence in Lp(Ω)such that

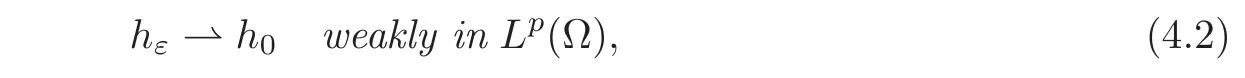
for some h0in Lp(Ω).Suppose further that F:R → R is a continuous function such that F(ψε)∈ Lq(Ω),with

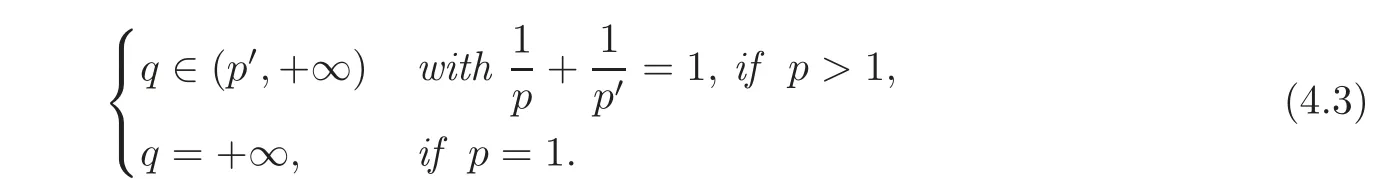
If

for some positive constant c independent of ε,then

Moreover,if

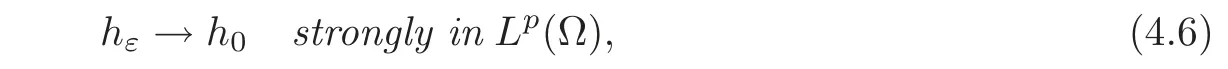
then

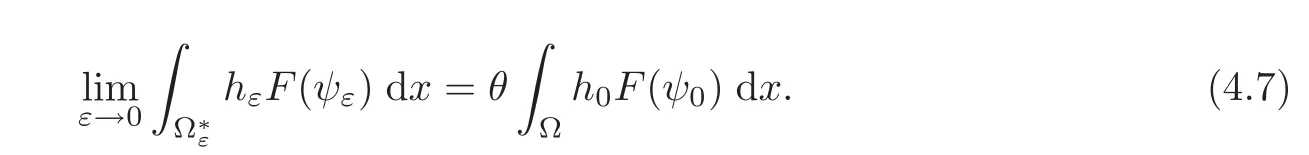
In particular,

weakly in Lp?(Ω)if p>1 and weakly ∗ in L∞(Ω)if p=1.

ProofConvergences(4.1)follow from Corollary 1.13,Corollary 1.19 and Theorem 2.13 of[11].

In order to show(4.5),let us first recall(see[11])that for any Lebesgue-measurable function φ on,the unfolding operatoris defined as

In view of Proposition 1.14 of[11],the assumption(4.2)implies that there exists some functionin Lp(Ω ×Y∗)such that

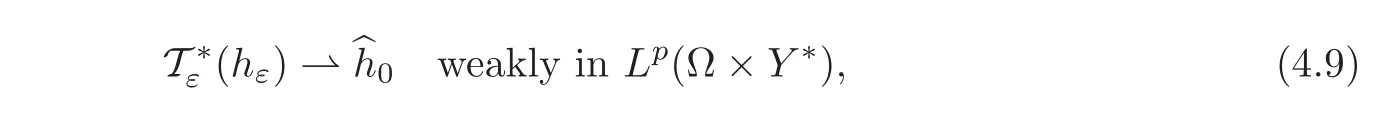
with

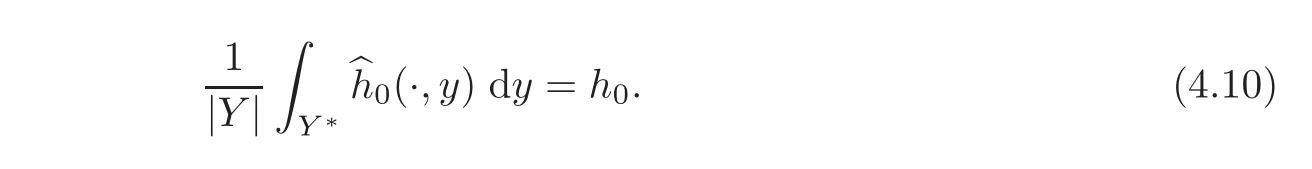
Using again Theorem 2.13 of[11],we derive that

Then,there exists a subsequence(still denoted by{ε})such that

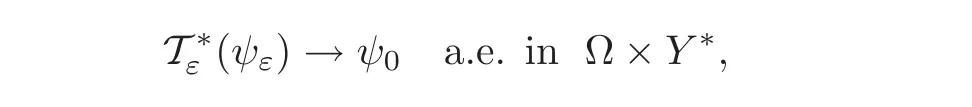
so that in view of the continuity of F,we get(for a subsequence)

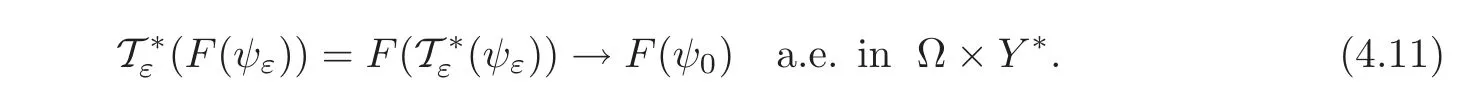
Moreover,using the properties of Tε(see[11,Proposition 1.12 and Corollary 1.13]),we deduce that

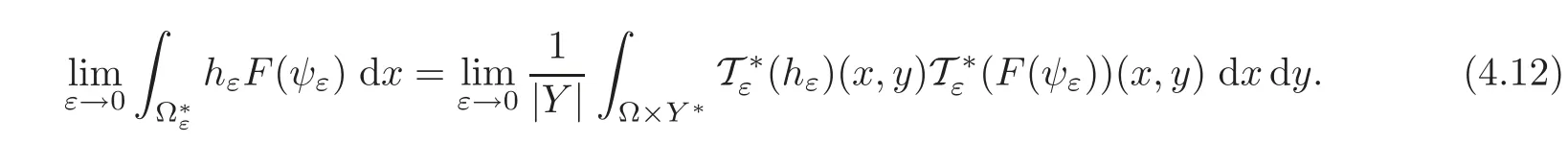
On the other hand,if p>1,thanks to(4.11),the H¨older inequality provides the equintegrability ofThen,using(4.4)we can apply the Vitali’s theorem to obtain

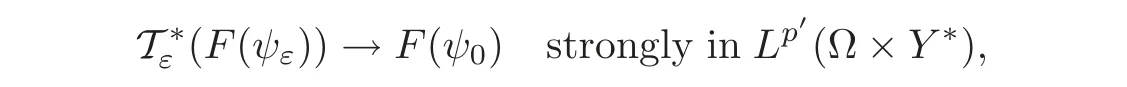
and this convergence holds for the whole sequence,since the limit is uniquely determined.

Consequently,from(4.9),we have

Since F(ψ0)is independent of y,in view of(4.10)this gives the result for p>1.

Let p=1 now.Then,thanks to(4.3)–(4.4),(4.9)and(4.11),we can still pass to the limit in the right-hand side of(4.12)by applying Lemma 3.1 in Ω ×Y∗,with gε=(hε)and tε=(ψε).We obtain again(4.13)and conclude as in the previous case.

Finally,observe that if(4.6)holds,from Corollary 1.19 of[11],one has=h0which implies that

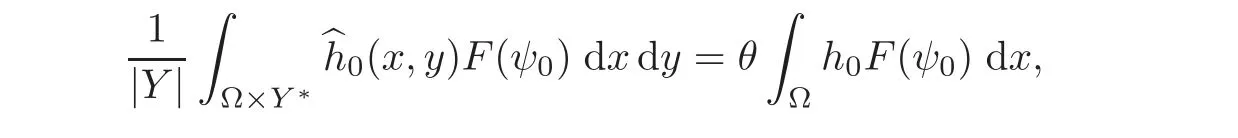
since θ=.This gives(4.7)and in particular(4.8)(taking hε=h0),which concludes the proof.

4.2 A corrector result for the nonlinear problem

In this section we prove Theorem 2.1.To do that,we adapt some arguments introduced in[4–5]for the case of oscillating coefficients in a fixed domain,and extended for the linear case in the periodically perforated domains in[19].We make here an essential use of Theorem 4.1,proved in the previous section.

The main idea is to define a suitable linear problem associated to a weak cluster point of the sequence of the solutions of problem(2.2)and then prove that the corrector for this linear problem is also a corrector for the original nonlinear problem.

Observe first that from(2.6)there exists a subsequence{uε}(still denoted by ε),which will be fixed from now on,and a function u0∈(Ω)∩L∞(Ω)such that

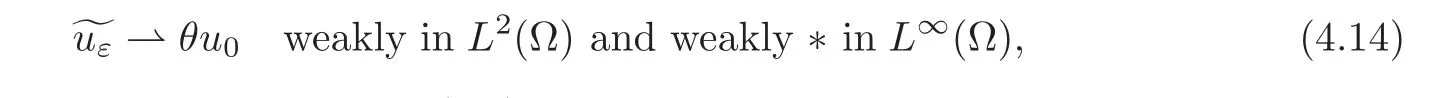
as ε tends to zero,where θ is defined by(2.1).

Then,in the present situation,the suitable linear problem associated to problem(2.2)is the following one:

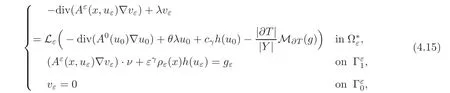
where Lεis a linear operator satisfying(H8).

Its variational formulation is

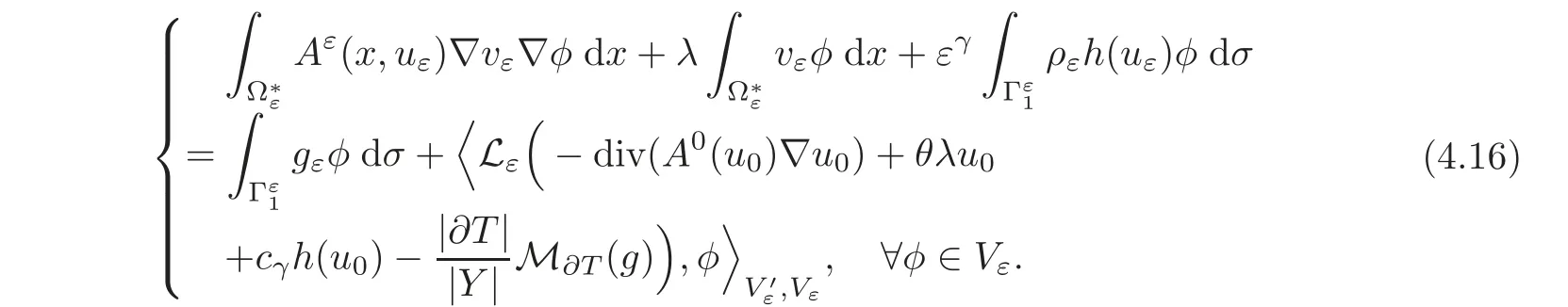
In view of Theorem 3.1,written for zε=uεand

using(4.14)we deduce that

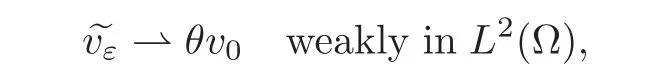
as ε tends to zero,where θ is defined by(2.1)and v0∈(Ω)is the unique solution of the equation

Hence,v0=u0,so that

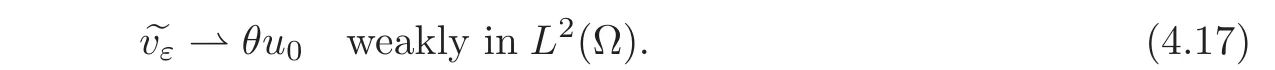
We approximate now the function u0∈(Ω)∩L∞(Ω)by a sequence{un} ⊂ D(Ω)such that

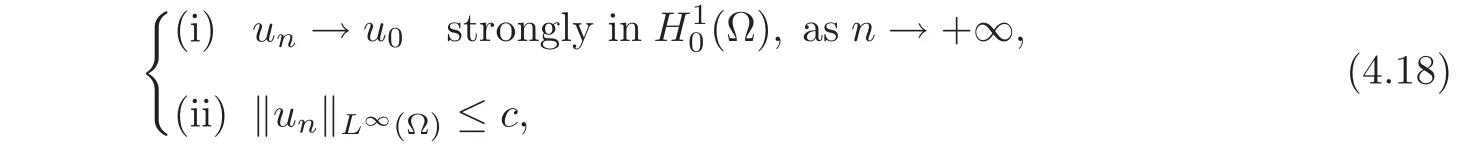
for any n,where c is independent of n.

Let us introduce,for any n ∈ N,the sequence{vn,ε}εwhere the function vn,εis the solution of the problem:

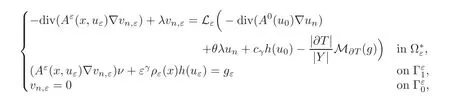
whose variational formulation is

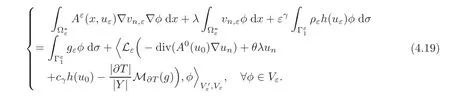
Then,for any n,we apply again Theorem 3.1,written here for zε=uεand for

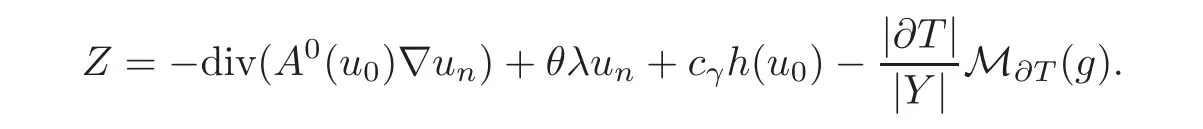
The same argument used to prove(4.17)gives

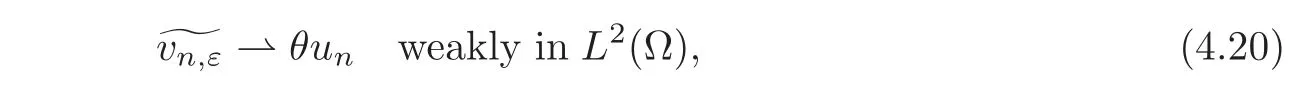
as ε tends to zero,where θ is defined by(2.1).Moreover,

where c is independent of n and ε,and from the classical results of Stampacchia[24],for any fixed n,we have

where cnis a constant independent of ε.

The following theorem is the essential tool to prove the corrector result for the nonlinear problem.

Theorem 4.2Under the assumptions(H1)–(H7),let uεbe a sequence of solution of problem(2.5)and vεbe a solution of problem(4.19).Then,up to a subsequence,we have

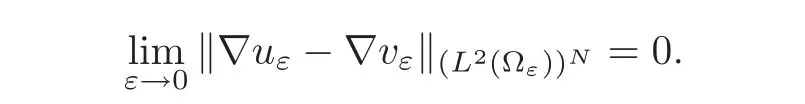
ProofLet Φεbe the function defined by

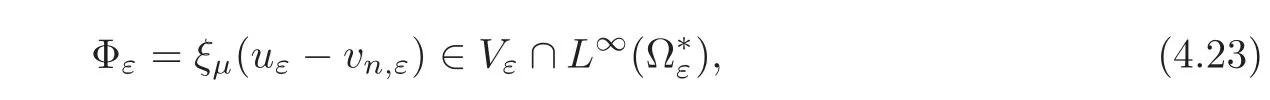
where μ is a suitable positive constant to be chosen later on,and

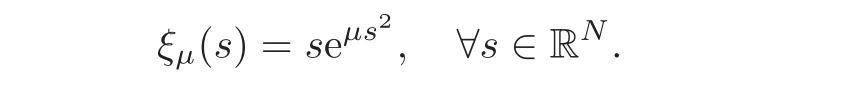
Taking Φεas a test function in(2.5)and(4.19),after subtraction of two identities,we obtain

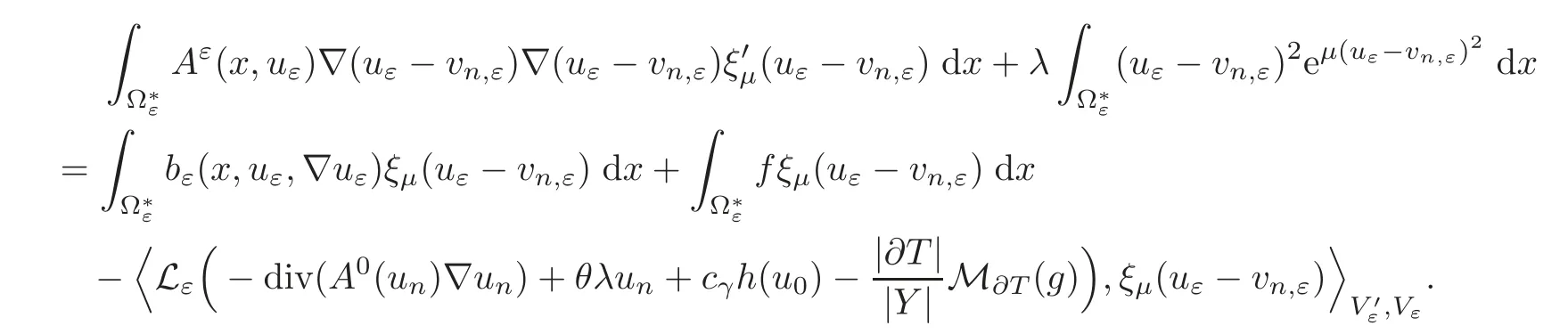
Using(H1),(H3)and the property(2)of(H7),since ξ?μ≥0,we get

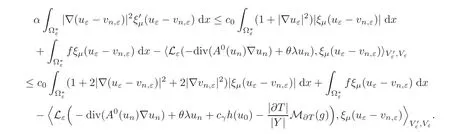
Let us take μ=.For this choice,one gets(s)−2c0|ξμ(s)|≥for any s,so that using again(H3),we get

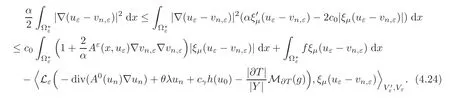
From(2.6),(4.21)–(4.22),the function uε−vn,εsatisfies(3.1)and the sequence{ξμ(uε−vn,ε)}is bounded in L∞(Ω)(for fixed n).

Hence,applying Theorem 4.1 to ψε=uε− vn,εand p=m, first with h=f and F= ξμ,and then with h=c0and F=|ξμ|,we obtain

Observe now that in view of Theorem 3.2 we can apply Theorem 4.1 for p=1 to the functions

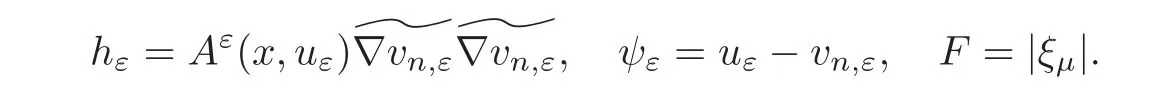
We get

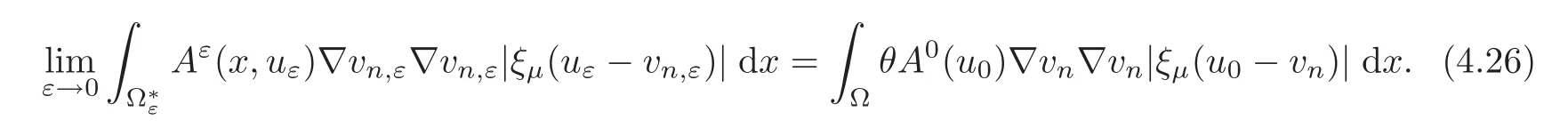
On the other hand,from(2.6)and(4.22)–(4.23),using again Theorem 4.1,we deduce that zε= ξμ(uε− vn,ε)satisfies(3.1)with z0= ξμ(u0− vn).

Then,the assumption(H8)given in Section 3 implies that

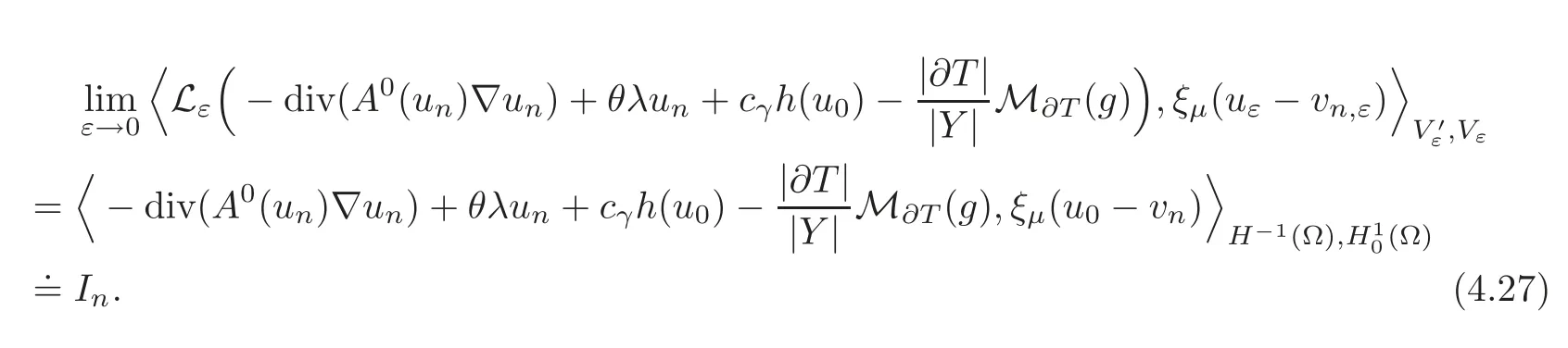
Collecting(4.24)–(4.27),we get

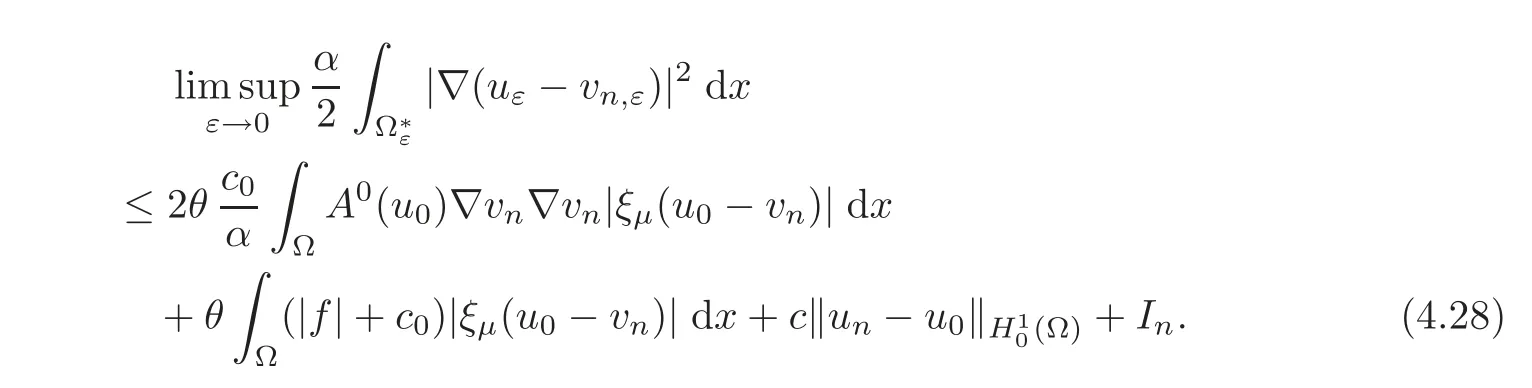
Hence,using(H2)–(H3),(4.18)and(4.23)we deduce that

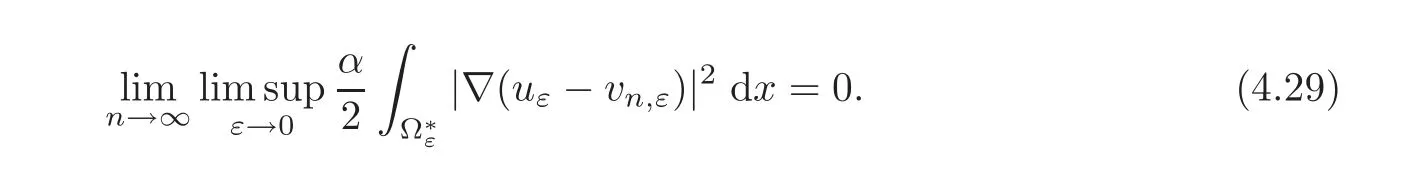
On the other hand,taking vn,ε− vεas test function in(4.16)and(4.19),subtracting the two identities and passing to the limit,one can easily deduce that

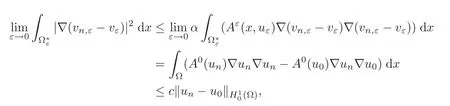
where the right-hand side goes to zero as n→∞,by virtue of(4.18).

This,together with(4.29),gives the result,since

4.3 Proof of Theorem 2.1

We distinguish here the two cases given by(2.4).

Let us treat first the case where M∂T(g)0 or g ≡ 0.Let{φn}n∈Nbe a sequence insuch that

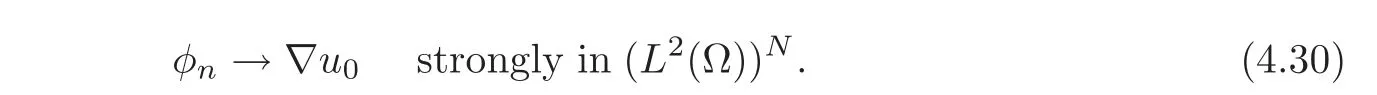
Then,for any ϕ ∈(Ω)∩ L∞(Ω),using(3)of(H7),(2.6)and(2.16),we get

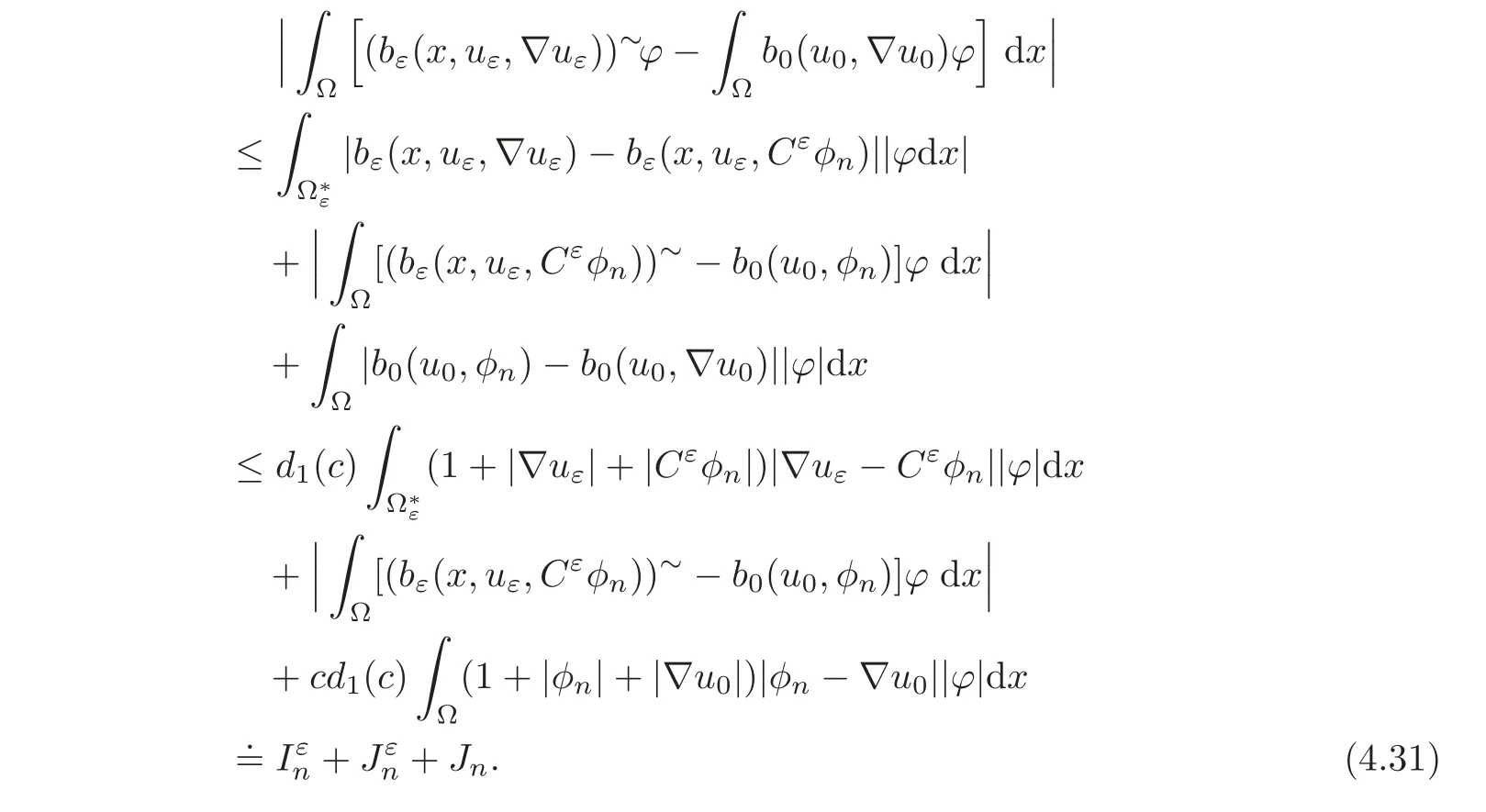
Let us pass to the limit as ε tends to zero in the right-hand side of this inequality.

Concerning the first term,by a similar argument as in[5,19],using(2.6),(2.12),(4.30),and Proposition 3.1,we have

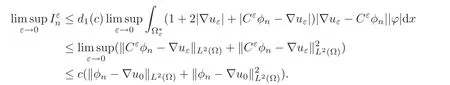
This,together with(4.30),implies

For the third term Jn(independent of ε),we have

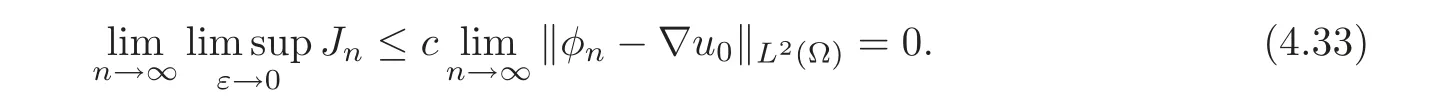
It remains to pass to the limit in the second term.To this aim,we write

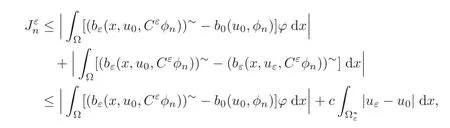
where we used the assumption(H7)and again(2.12)and(4.30).

Consequently,by Proposition 3.2 and Theorem 4.1,

Hence,by(4.31)–(4.34)for any ϕ ∈(Ω)∩ L∞(Ω),we have

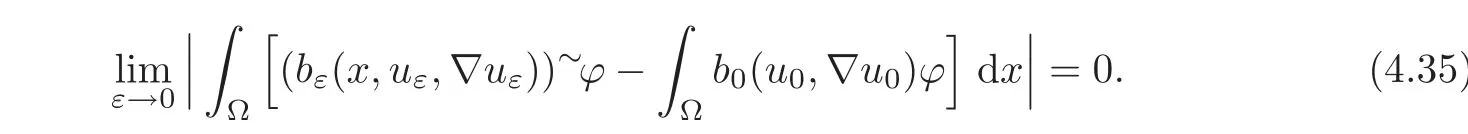
Moreover,from(2.1)and(4.14),we derive

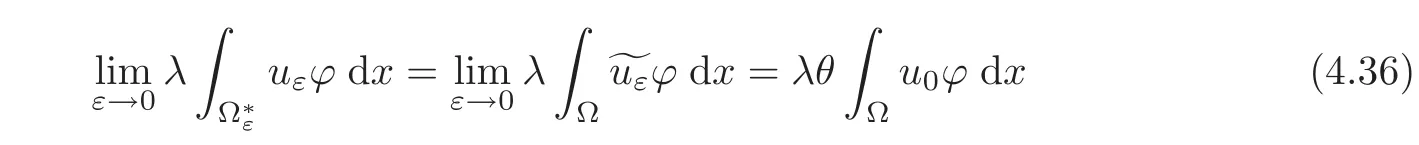
and

On the other hand,using the unfolding periodic method and arguing as in[10](see also[8]),we get

where cγis defined by(2.15)and

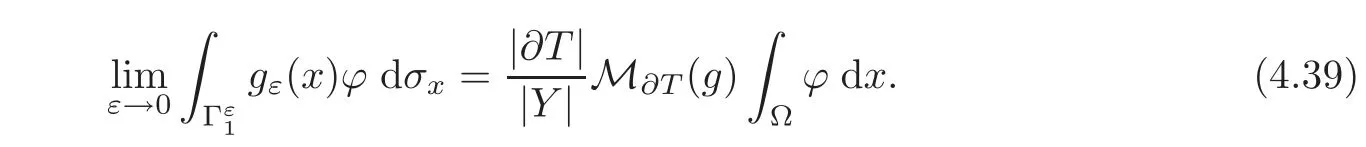
Let us prove now(2.17).For any ψ ∈(Ω),from Theorem 4.2,the assumption(H3)and the H¨older inequality,we obtain

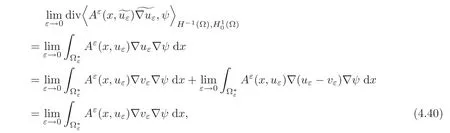
where vεis the solution of problem(4.15).

On the other hand,thanks to(3.5)(ii)and(4.17),we can apply Theorem 3.1(written for zε=uεand z0=v0=u0)to problem(4.15)and we have

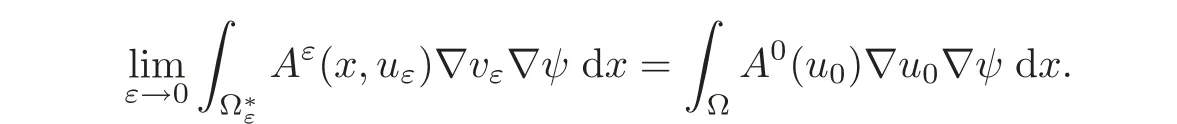
This together with(4.40)gives(2.17).

Hence,using(2.17)and(4.35)–(4.39),we can pass to the limit in(2.5)for any ϕ in(Ω)∩L∞(Ω)and obtain

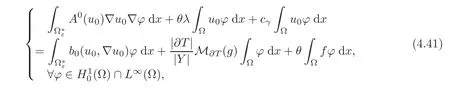
where b0is given by(2.16),i.e.,the variational formulation of the homogenized problem(2.18).

Let us consider now the case M∂T(g)=0 and that A is independent of t.Using(3)of(H3),for ϕ ∈(Ω)∩ L∞(Ω),we write here

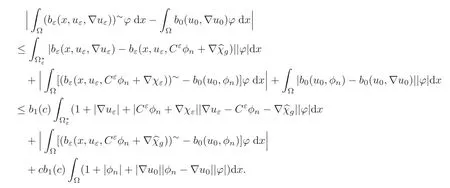
Then,arguing as before and using here the results corresponding to this case,we have

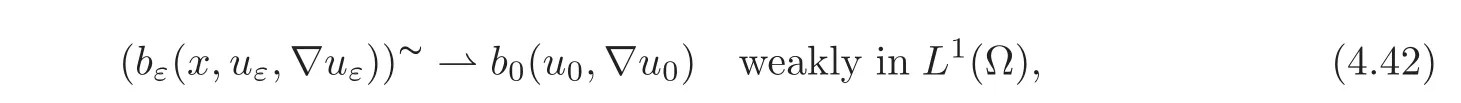
where b0is now given by(2.19).

On the other hand,(4.36)–(4.38)still hold true and from Proposition 3.8 of[10],

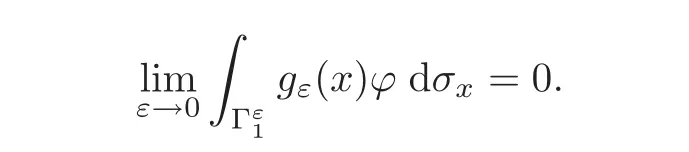
Finally,the convergence(2.21)follows as before by using(4.40).Hence,again we can pass to the limit in(2.5)for this case,to obtain

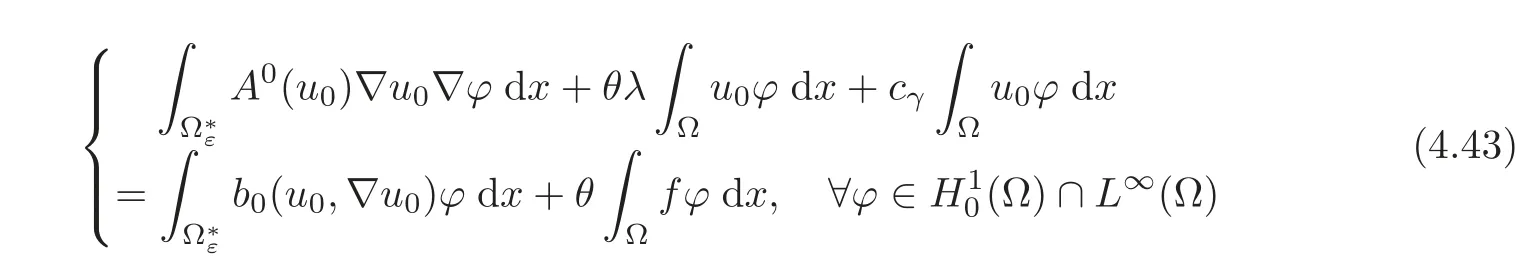
with b0given by(2.19),which is the variational formulation of the homogenized problem(2.18).This ends the proof of Theorem 2.1.

[1]Artola,M.and Duvaut,G.,Homogénéisation d’une classe de problèmes non linéaires,C.R.Acad.Paris Série A,288,1979,775–778.

[2]Artola,M.and Duvaut,G.,Un résultat d’homogénéisation pour une classe de problèmes de diffusion non linéaires stationnaires,Ann.Faculte Sci.Toulouse,IV,1982,1–27.

[3]Bendib,S.,Homogénéisation d’une classe de problèmes non linéaires avec des conditions de Fourier dans des ouverts perforés,Institut National Polytechnique de Lorraine,2004.

[4]Bensoussan,A.,Boccardo,L.,Dall’Aglio,A.and Murat,F.,H-convergence for quasilinear elliptic equations under natural hypotheses on the correctors,Proceedings of the Conference Composite Media and Homogenization Theory,Trieste,1993.

[5]Bensoussan,A.,Boccardo,L.and Murat,F.,H-convergence for quasi-linear elliptic equations with quadratic growth,Appl.Math.Optim.,26,1992,253–272.

[6]Bensoussan,A.,Lions,J.L.and Papanicolaou,G.,Asymptotic Analysis for Periodic Structures,AMS Chelsea Publishing,Amsterdam,1978.

[7]Boccardo,L.and Murat,F.,Homogénéisation de Problèmes Quasi linéaires,Atti del convergno,Studio di Problemi-Limite dell’Analisi Funzionale(Bressanone 7–9 sett.1981),Pitagora Editrice,Bologna,1982,13–51.

[8]Cabarrubias,B.and Donato,P.,Homogenization of a quasilinear elliptic problem with nonlinear Robin boundary conditions,Applicable Analysis,91(6),2012,1111–1127.

[9]Chourabi,I.and Donato,P.,Bounded solutions for a quasilinear singular problem with nonlinear Robin boundary conditions,differential and Integral Equations,26(9–10),2013,975–1008.

[10]Chourabi,I.and Donato,P.,Homogenization and correctors of a class of elliptic problems in perforated domains,Asymptotic Analysis,92(1),2015,1–43,DOI:10.3233/ASY-151288.

[11]Cioranescu,D.,Damlamian,A.,Donato,P.,et al.,The periodic unfolding method in domains with holes,SIAM J.Math.Anal.,44(2),718–760.

[12]Cioranescu,D.,Damlamian,A.and Griso,G.,Periodic unfolding and homogenization,C.R.Acad.Sci.Paris,Ser.I,335,2002,99–104.

[13]Cioranescu,D.,Damlamian,A.and Griso,G.,The periodic unfolding and homogenization,SIAM J.Math.Anal.,40(4),2008,1585–1620.

[14]Cioranescu,D.,Donato,P.and Zaki,R.,The periodic unfolding and Robin problems in perforated domains,C.R.Acad.Sci.Paris,Ser.I,342,2006,467–474.

[15]Cioranescu,D.and Donato,P.,Homogénéisation du probléme de Neumann non homogène dans des ouverts perforés,Asymptot.Anal.,1,1988,115–138.

[16]Cioranescu,D.,Donato,P.and Zaki,R.,The periodic unfolding method in perforated domains,Portugal Math.,63(4),2006,476–496.

[17]Cioranescu,D.,Donato,P.and Zaki,R.,Asymptotic behavior of elliptic problems in perforated domains with nonlinear boundary conditions,Asymptot.Anal.,53,2007,209–235.

[18]Cioranescu,D.and Saint Jean Paulin,J.,Homogenization in open sets with holes,J.Math.Anal.Appl.,71,1979,590–607.

[19]Donato,P.,Gaudiello,A.and Sgambati,L.,Homogenization of bounded solutions of elliptic equations with quadratic growth in periodically perforated domains,Asymptotic Anal.,16(3–4),1998,223–243.

[20]Donato,P.and Giachetti,D.,Homogenization of some singular nonlinear elliptic problems,International Journal of Pure and Applied Mathematics,73(3),2011,349–378.

[21]Donato,P.and Yang,Z.Y.,The period unfolding method for the wave equations in domains with holes,Advances in Mathematical Sciences and Applications,22(2),2012,521–551.

[22]Meyers,N.G.,An Lp-estimate for the gradient of solution of second order elliptic divergence equations,Ann.Sc.Norm.Sup.,17,1963,189–206.

[23]Murat,F.,H-convergence,Séminaire d’analyse fonctionnelle et numérique,Université d’Alger,1978.

[24]Stampacchia,G.,Le problème de Dirichlet pour leséquations elliptiques du second ordre à coefficients discontinus,Ann.Inst.Fourier,15(1),1965,189–258.