Rational Structure of X(N)over Q and Explicit Galois Action on CM Points∗

Tonghai YANG

1 Introduction

Let g≥1 and N≥1 be positive integers,and let Hgbe the Siegel upper half plane of genus g,i.e.,the set of symmetric complex matrices τ of order g such that?(τ)>0.Let

be the main congruence subgroup and let X(N)=Γ(N)Hgbe the complex manifold which turns out to be an algebraic variety.To construct a cryptosystem by using genus g(g=1,2)CM curves,it is important to compute a CM point in X(N)and its Galois conjugates in X(N)explicitly so that one can compute f(τ)explicitly for some explicit modular functions(invariants)f on X(N).For this,one needs to interpret X(N)in terms of moduli.There are two well-known moduli schemes:X0over Q(μN)whose C-points give X(N),and X over Q whose C-points give(Z/N)×-copies of X(N)(see Section 2 for a review),which are thus not connected.Here μNis the group of N-th root of unity.Neither one is handy for our purpose as the first one is only defined over Q(μN)and the second one has extra(Z/N)×in addition to X(N).There turns out to be a third non-standard moduli scheme X∗over Q,whose C-points also give X(N),which is natural and good for our purpose.This is constructed as a quotient of X in Section 2.This moduli interpretation is a special case of the general Shimura variety construction,though not explicitly presented in the literature and it should be of interest to publicize it.Using this interpretation,we give an explicit Galois action on a CM point in X(N)in Section 3.As a byproduct,we give in Section 4 a direct proof of the well-known Shimura reciprocity law,which Shimura developed in the 1970s(see for example[6]),and its explicit version given by Streng recently(see[10]).

This work was inspired by my joint work with Castello,Deines-Shartz,and Lauter[1]on genus two curues.

2 Open Modular Variety X(N)over Q

Let G=GSpgbe the generalized symplectic group(matrices of order 2g)with a similitude character μ,and let G0=Spgbe the usual symplectic group,i.e.,the kernel of μ:

There are two well-known moduli spaces associated with X(N)which we now brie fly review,and refer to[2]for a thorough review.Let μNbe the group of the N-th roots of unity in C, fix an isomorphism μNZ/N and identify them in this paper.Then for any principally polarized abelian variety A over a field F(of a character prime to N),the Weil pairing on the N-torsion A[N]becomes a symplectic pairing

which is perfect if A[N](F)=A[N].

Let X be the moduli space over Z[]as follows:For a Z[]-scheme S,X(S)consists of isomorphism classes of the triplets(A,λ,φ),where

(1)A is an abelian scheme over S,

(2)λ:A→A∨is a principal polarization of A,and

(3)φ :(Z/N)2g→ A[N](S)is locally a similitude symplectic isomorphism,i.e.,?φ(x),φ(y)?we=d?x,y?for some d ∈ (Z/N)×(both φ and d may vary,depending on local connected components of S).Here we use the standard sympletic form on(Z/N)2g:

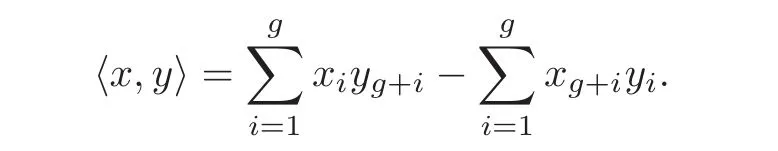
Notice that due to the freedom on d ∈ (Z/N)×,the moduli problem does not depend on the choice of our identification μNZ/N.It is well-known that this moduli space is represented by a smooth Deligne-Mumford stack,still denoted by X,over Z[].It is actually a smooth scheme when N≥3.

Let X0be the moduli space over Z[,μN]as follows:For a Z[,ζN]-scheme S,X(S)consists of isomorphism classes of the triplets(A,λ,φ),where

(1)A is an abelian scheme over S,

(2)λ:A→A∨is a principal polarization of A,and

(3)φ :(Z/N)2g→ A[N](S)is a symplectic isomorphism,i.e.,?φ(x),φ(y)?we=?x,y?.

It is also well-known that this moduli space is represented by a smooth Deligne-Mumford stack,still denoted by X0,over Z[,μN].It is again a smooth scheme when N ≥ 3.

In terms of the Shimura datum,one has the following:Let

Then X is the Shimura variety associated with K,i.e.,

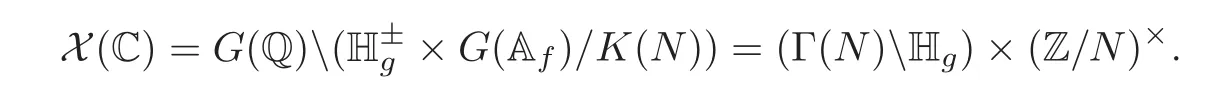
Moreover,

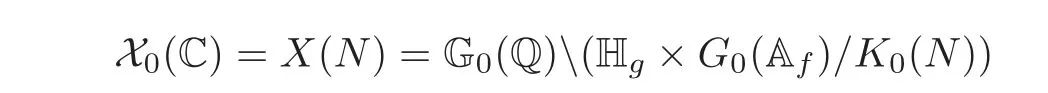
is the connected component of X(C).

It turns out that there is a(less known)third Shimura variety X∗over Z[]directly related to X(N).It is associated with the compact open subgroup of G

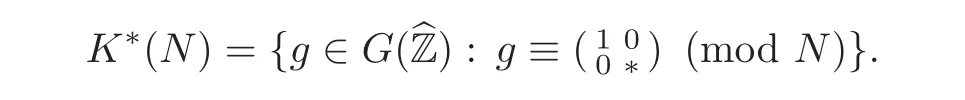
By the strong approximation theorem,one has

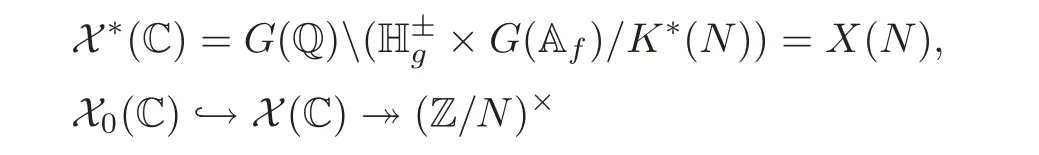
and

Here the action is given by d◦[z,g]=[z,gv(d)],and the natural project from X(C)to X∗(C)has fiber(Z/N)×.Here v(d)=()with respect to the standard symplectic basis of(Z/N)2g.

To give the moduli problem for this variety,let(Z/N)×act on X as follows:

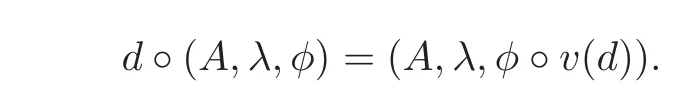
The action is free,so there is a quotient stack(a scheme for N ≥3)X∗=X/(Z/N)×which represents the following quotient moduli problem over Z[].For a Z[]-scheme S,X∗(S)consists of the equivalence classes of the triples(A,λ,φ)as in X(S),but with the following equivalence relation:(A1,λ1,φ1) ∼ (A2,λ2,φ2)if and only if there is an S-isomorphism f:A1→ A2commuting with the polarizations λiand φ2= φ1◦ v(d)for some d ∈ (Z/N)×.Alternatively,X∗(S)are the equivalence classes of the triples(A,λ,?e)where(A,λ)is a principally polarized abelian scheme over S,and?e=(e1,···,e2g)is locally an ordered similitude symplectic basis of A[N](S)with respect to the Weil pairing,i.e.,for i≤j,

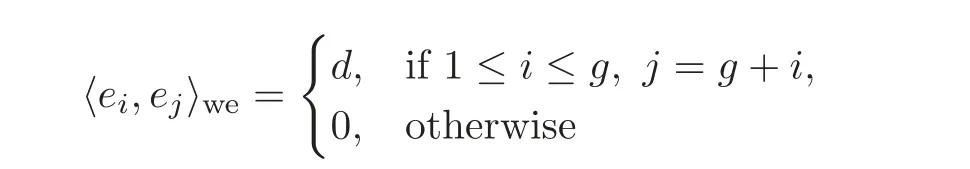
for some d ∈ (Z/N)×.A similitude symplectic basis is called a symplectic basis if d=1.Two such triples(A,λ,?e)∼ (A?,B?,?e?)if and only if there is an S-isomorphism f:(A,λ)→ (A?,λ?)such that f(ei)=for 1≤i≤g and f(ei)=for all g+1≤i≤2g and some d∈(Z/N)×locally.

Proposition 2.1One has,over Z[,μN],

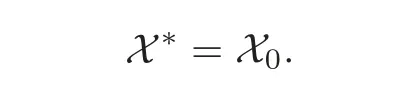
ProofLet=(e1,e2,···,e2g)be the standard symplectic basis of(Z/N)2g.Given two triples(A,λ,φ)and(A?,λ?,φ?)in X0(S)for a Z[,μN]-scheme S,if they are equal in X∗(S),i.e.,there is an S-isomorphism f:(A,λ)→ (A?,λ?)and d ∈ (Z/N)×such that φ?=f ◦φ◦v(d),one has

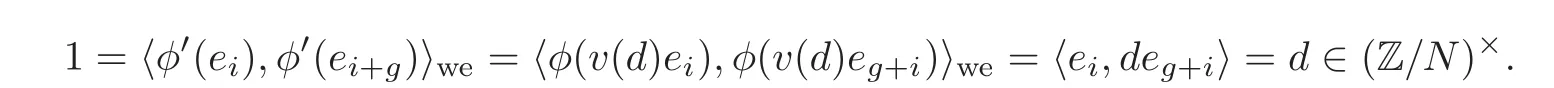
So(A,λ,φ)=(A?,λ?,φ?)in X0(S).This gives an injection X0→ X∗over Z[1N,μN].To verify the surjectivity,let(A,λ,φ)∈ X∗(S).Let Pi= φ(ei),and then there is d ∈ (Z/N)×such that

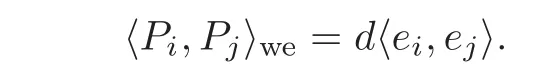
Take φ?= φ ◦ v(d−1),and then one sees that φ?is a symplectic isomorphism.So(A,λ,φ)=(A,λ,φ?)∈ X∗(S)is the image of(A,λ,φ?)∈ X0(S).

Remark 2.1There is another moduli interpretation for X(N)over Q as follows:Let X?be the moduli space of the equivalence classes of the triples(A,λ,φ),where(A,λ)are principally polarized abelian schemes as above,and φ :(Z/N)g×(μN)g→ A[N]is a Galois equivariant map which respects the pairings.The equivalence is the usual one as in the moduli interpretation of X.Here the pairing at the right-hand side is the Weil pairing while the one at the left-hand side is the obvious one

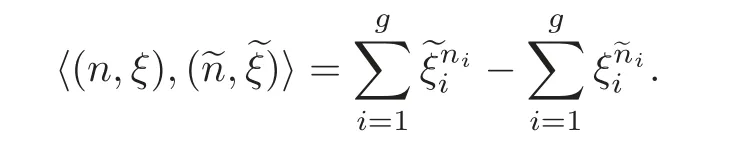
The natural maps

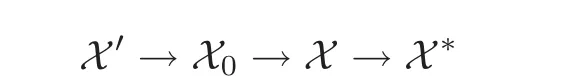
are defined over Q(μN).One can prove that the composition X?→ X∗is actually an isomorphism defined over Q.This remark belongs to the anonymous referee.

Remark 2.2The moduli variety X∗is quite natural both in terms of the Shimura datum and in terms of moduli interpretation.It is curious and a bit strange that it has not appeared in any literature to my best knowledge.For example,it could have naturally been in[3,Table(7.4.3)],as its analogues for Γ1(N)and Γ0(N)are both there.

Remark 2.3If we let N change,temporarily write X(N)for X and take the inverse limit,then the pro-Shimura varietyis a right G(Af)-module,but far from connected.On the other hand,is a connected quotient of X.However,only the normalizer ofin G(Af),not the whole G(Af),can act on X∗.

3 Complex Multiplication and Galois Orbit of a CM Point

Let(E,Φ)be a CM number field with the CM type Φ,and let(?E,?Φ)be the re flex CM field with the re flex CM type.Let M be a Galois extension of Q containing both E and?E.Recall the type-norm on elements

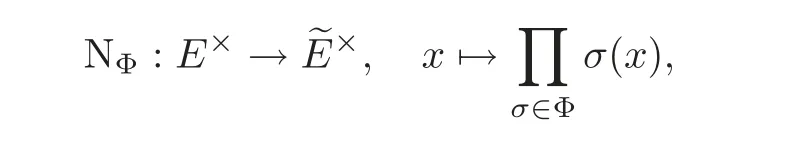
and on ideals

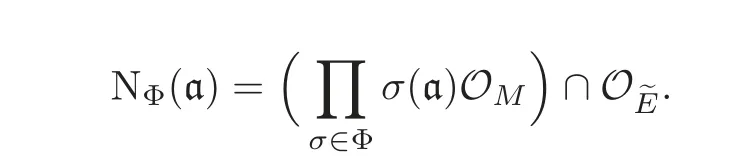
Here M is a(any)Galois extension of Q containing both E and?E.For the convenience of the reader,we first recall the well-known main theorem of Shimura and Taniyama on complex multiplication(see[7–8]).A CM abelian variety over a field L?→ C of the CM type(E,Φ)is in this paper a pair(A,ι),where A is an abelian variety over L of dimension[E:Q],ι:OE→ EndL(A)is an isomorphism,and there is a C basis{ωσ,σ ∈ Φ}on ΩA/Csuch that i(z)∗ωσ= σ(z)ωσ.For a number field E,we denote by Efthe finite adeles of E,and by?OEthe ring of integers of Ef.

Theorem 3.1(Shimura-Taniyama)Let b∈fand σ ∈such that=σb−1via the class field theory(the Artin map).Hereis the maximal abelian extension of.Let(A,ι)be a CM abelian variety over C of CM type(E,Φ).Then there is an isomorphism f:Cg/Φ(a)A for some fractional ideal a of E over C.Fix such an isomorphism f(and a),and there is a unique isomorphism f?:Cg/Φ(aN?Φb)→Aσover C such that the following diagram commutes:

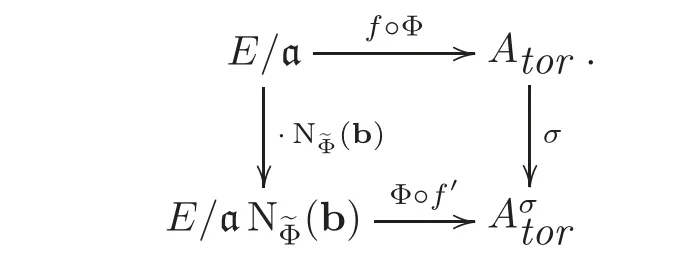
Here the multiplication by the idele in the column makes sense via the canonical isomorphism E/a=⊕pEp/ap.Here Ep(resp.ap)is the completion of E(resp.a)with respect to the prime ideal p.

A CM point of the CM type(E,Φ)in X∗(L),for a field L ⊂ C,is a tuple(A,ι,λ,φ)where(A,ι)is a CM abelian variety of the CM type(E,Φ)and(A,λ,φ) ∈ X∗(L)such that the Rosati involution associated to λ induces the complex conjugation on E.Let CM(E,Φ)be the set of CM points in X∗(C)=X(N)of the CM type(E,Φ).

Let R be a(communicative)ring,and let V be a free R-module of rank 2g with the nondegenerate symplectic form?,?.A basis=(a1,···,a2g)is called a similitude symplectic basis if the associated matrix

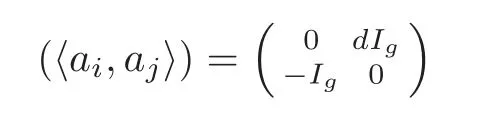
for some d∈R×.When d=1,we call it a symplectic basis.

Proposition 3.1There are bijections among the following sets:

(1)The set CM(E,Φ)⊂ X(N)of CM points of the CM type(E,Φ).

(2)The set of points[τ]∈ X(N)such that Λτ= τZg+Zg⊂ Cgis a(projective)OE-module via Φ ={σ1,···,σg},where E acts on Cgvia ι(z)x=diag(σ1(z),···,σg(z))x for z ∈ E and x∈Cg.

(3)The set of equivalence classes of(a,ξ,?a),where a is a fractional ideal of E,and ξ∈ E×such that= −ξ and a is integral and self-dual with respect to the symplectic pairing(the

Riemann form)

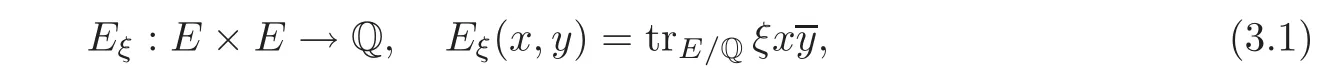
i.e.,=OE,where ∂Eis different from E.=(a1,···,a2g)is an ordered symplectic basis of a with respect to Eξ.Two triples(a,ξ,)and(b,η,)are equivalent if there is an r∈ E×and a γ ∈ Γ(N)such thatand

(3?)The set of equivalence classes of(a,ξ,),where a is a fractional ideal of E,ξ∈ E×such thatis a symplectic basis fora/a with respect to the Weil pairing

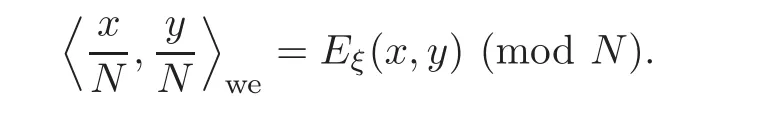
Two triplesandare equivalent if there is an r∈ E×such that rr ∈ Q×,and

(4)The set of equivalence classes of triples(Aa,Eξ,)where Aa=Cg/Φ(a)is a CM abelian variety of the CM type(E,Φ)over C,Eξ,as defined in(3.1),is a Riemann form on Aa,which gives a principally polarization on Aa,andis a similitude symplectic basis of Aa[N]=a/a with respect to the Weil pairing:

Two triples(Aa,Eξ,)and(Ab,Eη,)are equivalent if there is an r∈ E such that

Proof(Sketch)The bijection between(1)and(3)follows from X(N)=X0(C)and Theorem 3.1.The bijection between(1)and(4)follows from X(N)=X∗(C)and Theorem 3.1.The bijection between(3)and(3?)is due to the fact that SL2(Z)?SL2(Z/N)is surjective.Now we describe the bijection between(2)and(3).Recall that τ∈X(N)=X0(C)gives the triple(Aτ,Eτ,),where Aτ=Cg/Λτwith Λτ= τZg+Zgand the principal polarization Eτ=?Hτ,where

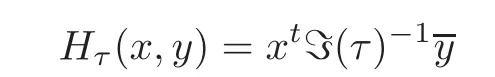
is the associated positive definite Hermitian form on Cg,and=(ei)1≤i≤2gwith

Notice thatis a symplectic basis of Λτwith respect to Eτ,and that Hτ(x,y)=Eτ(ix,y)+iEτ(x,y)(see for example[2,7]).

Given a triple(a,ξ,?a)in(3),let τ=(Φ(ag+1),···,Φ(a2g))−1(Φ(a1),···,Φ(ag)),also denoted by τ(a,ξ,?a).Then

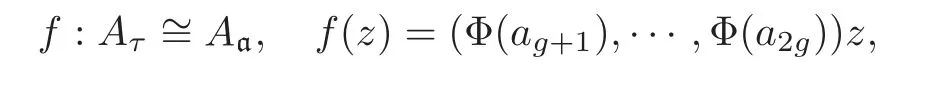
which sendsto.So(Aτ,Eτ,)=(Aa,Eξ,) ∈ X0(C)=X(N).Via the map f,ΛτΦ(a)becomes an OE-module.

Conversely,if Λτis an OE-module via Φ,then it isfinitely generated,torsion-free and thus projective of rank 1(comparing with the Z-rank).So there is a fractional ideal a of E and an OE-module isomorphism f:Φ(a)Λτ,which extends to an isomorphism f:AaAτ.The Riemann form Eτon Λτgives a self-dual sympletic form on a.So there is ξ such that a is Eξ-self-dual,and that= Φ−1f−1()is a symplectic basis of a.That is τ= τ(a,ξ,).This gives the bijection between(2)and(3).

We will identify each set in Proposition 3.1 with CM(E,Φ).Given(a,ξ,)∈ CM(E,Φ),we write the associated τ in X(N)as τ= τ(a,ξ,?a).It is given by

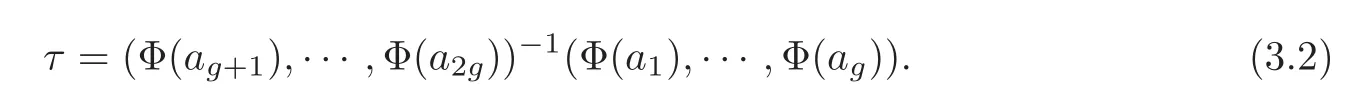
Viewingas a Q-basis of E,one obtains an embedding

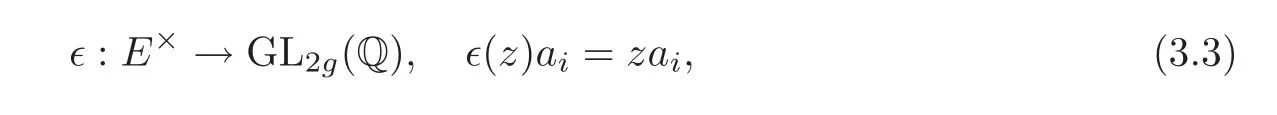
and a map

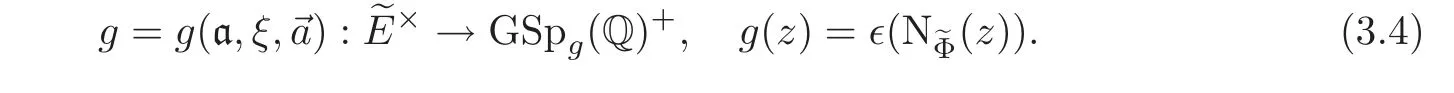
The map is well-defined as

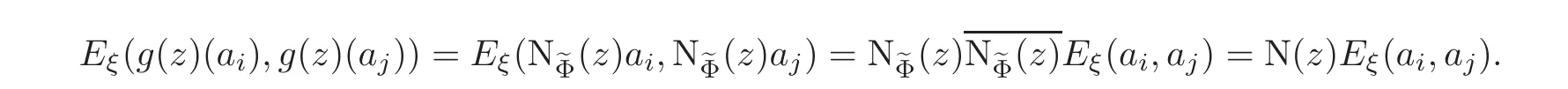
One has further μ(g(z))=N(z).The maps g and?depend on the point τ.

Let Cl(,N)be the type-class group of modulus N,defined as the quotient of all fractional ideals ofprime to N by the subgroup

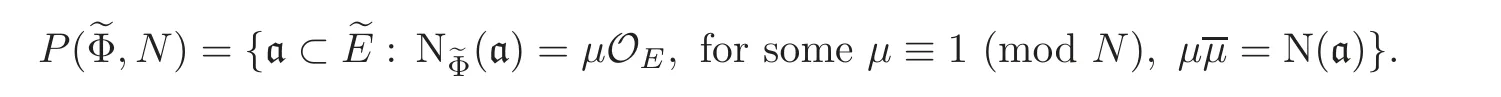
Let H(,N)be the associated type-class field of.For a number field E,we write Efas its finite adeles andas the ring of integers of Ef.The following isomorphism is well-known:

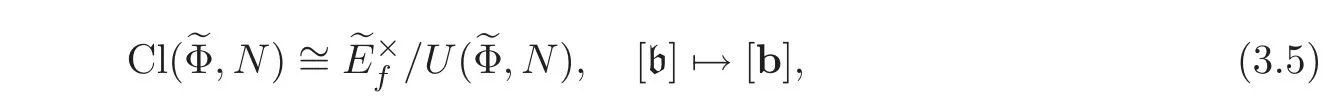
where b∈satisfies(b)==b and bp≡1(mod N)for all p|N.Here

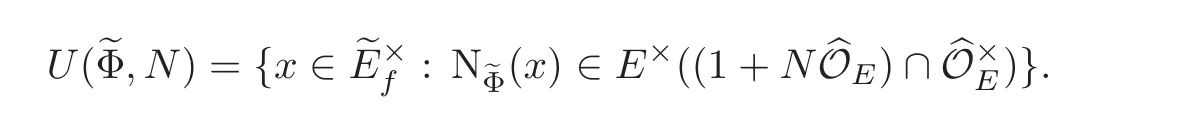
Proposition 3.2(1)For every CM point τ= τ(a,ξ,) ∈ X0(C),its field of definition is the class field H(,N).

(2)For a CM point τ=τ(a,ξ,)∈X∗(C),its field of definition is the class field H∗(,N)associated to the class groupwhere

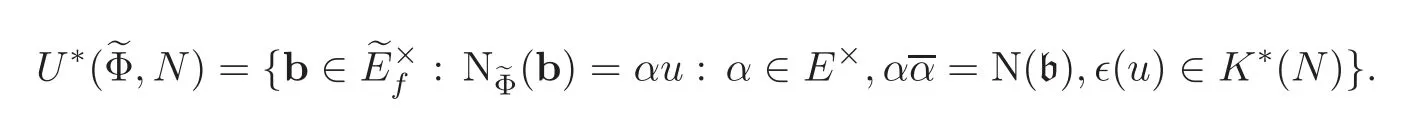
ProofThis proposition is a direct consequence of Theorem 3.1 and we give a sketch of(2)for convenience.Let σ∈Aut(C)with σ|H∗(?Φ,N)=σb−1via the class field theory.Here we use the normalization in[7]for the Artin map,i.e.,σp(x)≡ xN(p)(modp).Let b=(b)be the ideal of b.Assume τσ=τ,and thenAa.Sob=αOEfor some α ∈E×.Writeb=αu with u∈.So we have

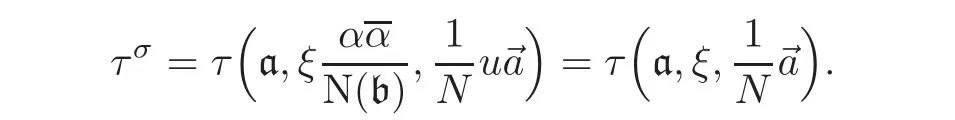
This implies that we can change α properly to make=N(b).Since the two symplectic similitude basesandofwith respect to the Weil pairing have to be equivalent,i.e.,differing only by v(d)for some d ∈ (Z/N)×,one has?(u)∈ K∗(N).The other way is the same.

Noticing that μN⊂andone has thatWe remark that the class fieldmight depend on the map?in(3.3),and thus the CM point τ.It is an interesting question whether and howreally depends on τ.For example,do different Galois orbits in CM(E,Φ)have the same cardinality?(or does the index[H∗(,N):]depend on τ?)

Theorem 3.2Let τ= τ(a,ξ,) ∈ CM(E,Φ) ∈ X(N)(C).Let σ ∈ Aut(C/E)and[b]∈Cl(,N)such that=σb−1via the class field theory.Choose an(ordered)symplectic basisof a(b)with respect to the symplectic form EξN(b)−1such that

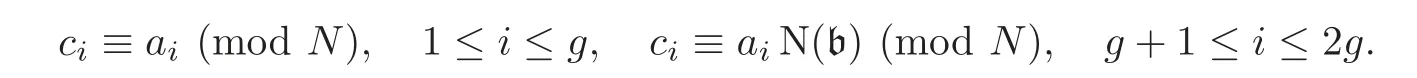
Then

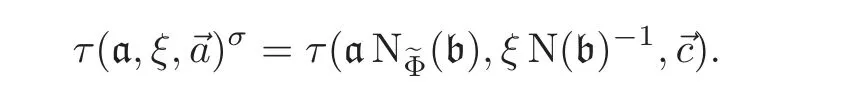
ProofChoose b∈such that(b)=b and bp=1 for all primes ofabove N,as in(3.5).We may assume that b is integral.Then Theorem 3.1 implies

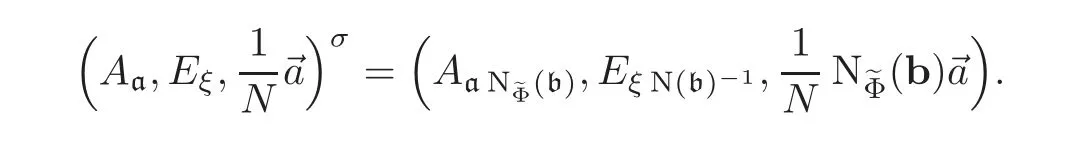
Notice

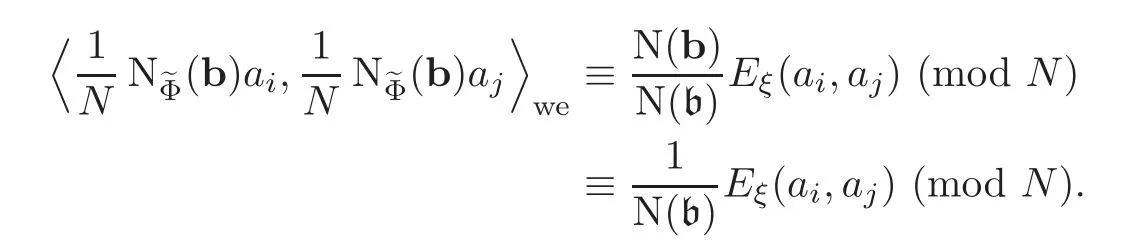
So one has in

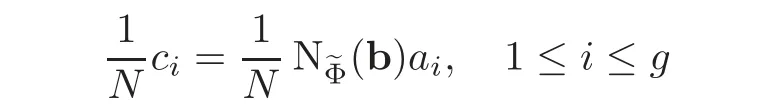
and

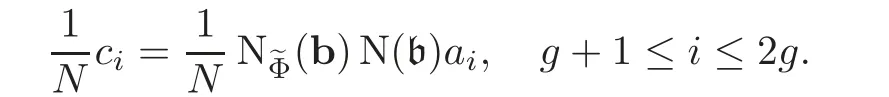
SoIndeed,for a prime p of E above N,it is true by our choice of?c and by the fact=1.For p?N,both sides are zero.Therefore,

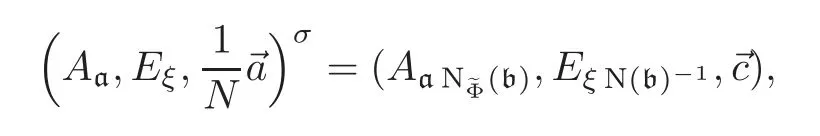
i.e.,

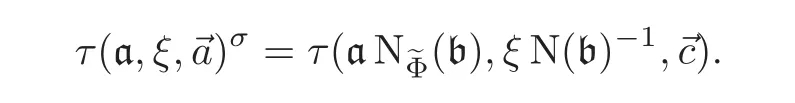
Let f(τ)be a memormorphic modular function on Hgfor Γ(N),viewed also as a rational function on X∗(C),and let

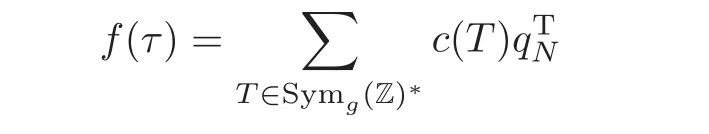
be the Fourier expansion of f(τ)with c(n)∈ C and=e(trTτ).For σ ∈ Aut(C),fσ,as a rational function on X∗(C),is defined to satisfy the following condition:For every P ∈ X∗(C),one has

By the q-expansion principle,fσhas the following Fourier expansion:

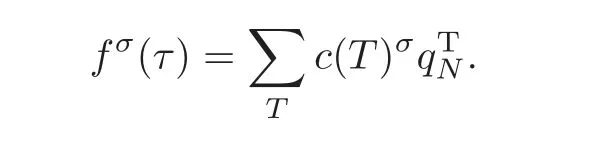
Now the following explicit Galois action formula on CM values follows directly from Theorems 3.1–3.2.

Corollary 3.1Let f(τ)be a memomorphic modular function on Hgfor Γ(N)(also momomorphic at cusps).Let τ= τ(a,ξ,) ∈ CM(E,Φ)be a CM point on X(N).Let σ ∈ Aut(C/),and let[b]∈Cl(,N)such thatThen

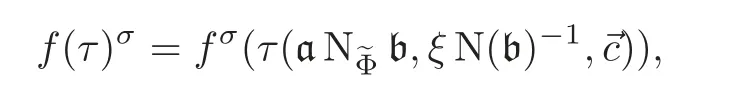
where τ(aN?Φb,ξ N(b)−1,?c)=τσis given as in Theorem 3.2.

ProofLet X be a toriodal compactification of X∗/Q which is a projective algebraic variety.By our assumption,f is a rational function on X.So f(τ)σ=fσ(τσ),and the first claim follows directly from Theorem 3.1.

The case N=2 and g=2 was used in[1]and is the initial motivation for this work.

Remark 3.1It should be very interesting to work out the whole Galois orbit of a CM point under Aut(C/Q).It should be doable by using Deligne and Langlands’generalization of Theorem 3.1(see[4]).

Remark 3.2There is another group acting on CM(E,Φ).Let

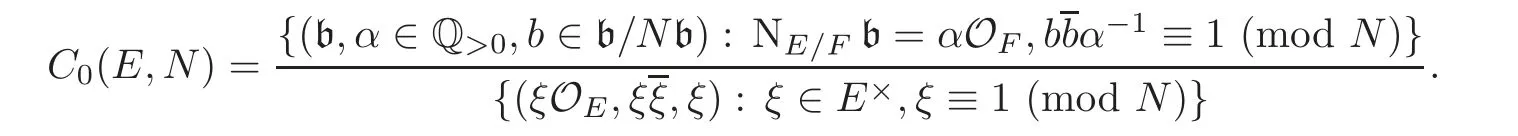
The action is given as follows:

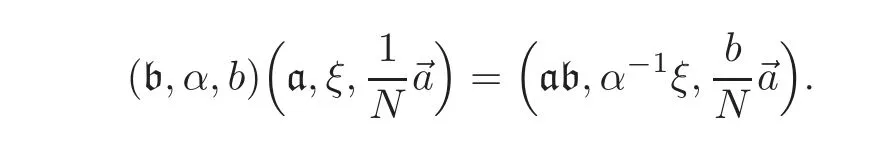
4 Reciprocity Law

In this section,we will use Corollary 3.1 to give another proof of Streng’s explicit Shimura reciprocity law and the original Shimura reciprocity law.We need some notations before stating their theorems(see[5–6,10]).We will mainly follow[10]in the review and refer to it for more details.Let FNbe the field of meromorphic Siegel modular functions,where gi(i=1,2)are holomorphic Siegel modular forms of level N and of the equal weight with Fourier coefficients in Q(μN),and g2?0.By the q-expansion principle,one has FN=Q(μN)(X0)=Q(μN)(X∗).Let F∞= ∪FN.The following proposition is due to Shimura(see[10,Propositions 2.1 and 3.1]).Let G(R)+be the subgroup of G(R)with μ(g)>0,G(A)+=G(Af)× G(R)+and G(Q)+=G(R)+∩ G(Q).Recall G=GSpg(GSp2gin Streng’s notation).

Proposition 4.1(a)There is a unique action of G(A)+on F∞satisfying the following conditions:

(1)For γ ∈ G(Q)+,one has fγ(τ)=f(γτ).

(2)For x ∈ A×,one has fv(x)=fσx.Here σx∈ Gal(Q(μ∞)/Q is the Artin map image of x via the class field theory,v(x)=diag(Ig,xIg),and fσ(τ)is the new modular function with σ acting on the Fourier coefficients of f.

(3)For any N ≥ 1,the group K(N)×G(R)×acts on FNtrivially.Here we recall that K(N)is the compact open subgroup of G(Af)defining X.

(b)There is a unique action of G(Z/N)on FNas follows:

(1)The action of Spg(Z/N)on FNis given by fγ(modN)=fγfor γ ∈ Spg(Z),where fγis given by(a)(1)above.

(2)For any x ∈ (Z/N)×,fv(x)=fσx.

Now we are ready to give a direct proof of Streng’s explicit reciprocity law(without using Shimura’s reciprocity law).Please note that we only deal with the case of the maximal order of E while Shimura and Streng dealt with the general case,though our method works in general too.

Theorem 4.1(see[10,Theorem 2.4])Let τ= τ(a,ξ,?a) ∈ X(N)be a CM point of the CM type(E,Φ)as before.Let σ=σb−1∈Gal(H(,N)/).Letbe a symplectic basis of aN?Φ(b)with respect to EξN(b)−1.Let M ∈ GSpg(Q)+such that.Then M is N-integral and invertiable modulo N.Let U=M−1(mod N)∈GSpg(Z/N).Then for any f∈FN,one has

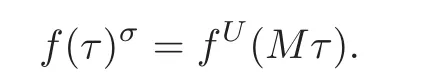
ProofBy Corollary 3.1,one has

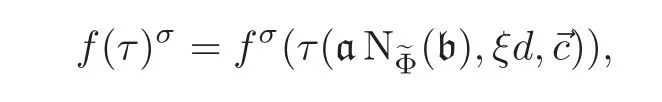
where d=N(b)−1and?c is the symplectic basis of a(b)with respect to Edξgiven in Theorem 3.2.Let Cl(Z,N)be the ray class group of Q with modulus N,and its associated class field is Q(μN).Notice that the norm map fromto Cl(Z,N)is surjective which also explains Q(μN)⊂H(?Φ,N).So by the class field theory,one has Q(μN)⊂,and

So fσ=fσd=fv(d),and

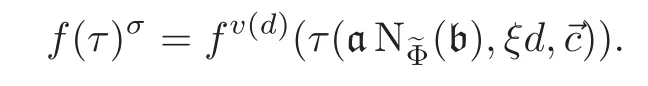
Let γ∈Spg(Z)such thatThenOn the other hand,and thus μ(U)=d(mod N),and(mod N).So

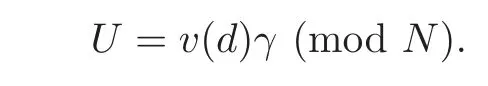
Therefore

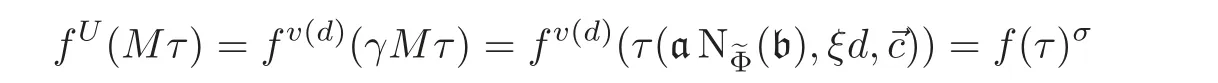
as claimed.

Finally,we derive Shimura’s reciprocity law in its original adelic form(see[6,P.57]).Letas before.Recall the maps?and g in(3.3)–(3.4).The following is the Shimura’s reciprocity law(see[6,P.57],see also[10,Theorem 3.4]).

Theorem 4.2(Shimura)Letbe a CM point of the CM type(E,Φ),and let g:→GSpg(A)+be the adelization of the map g defined in(3.4).Then for any f∈F∞such that f(τ)isfinite,and for any b∈,we have

ProofWe can choose N big enough so that f ∈ FN,and then view τ as a CM point on X(N).So f(τ)∈H(,N),and both sides of the identity depend only on the idele class[b]Therefore we may assume that bp=1 for all primes of?E above N,and let b=(b)be the fractional ideal ofassociated to b.Letas in Theorem 3.2.We writeand g=g(b).Thenhas two similitude symplecticand(with respect to Eξ).So there is γ ∈GSpgsuch thatandLet M= γ−1g ∈ GSpg(Af)with μ(M)=N(b).Since?a and?c=M(?a)are both similitude symplectic Q-bases of E(with respect to Eξ),one has M ∈ GSpg(Q)+.WritewithRecalling the condition on?c in Theorem 3.1 and that bp=1 for all p|N,one sees that γ1maps?a to?a modulo N.So γ1≡ 1(mod N).Now(since we write elements in G as maps in the proof,this order of decomposition is correct),and one has by Proposition 4.1 that

as claimed.

AcknowledgementsThis work was motivated while I was working with Castello,Deines-Shartz,and Lauter during my Microsoft visit in Fall 2013.I thank them for the inspiration and the joint work.During that time,I did not realize the existence of Streng’s excellent work on explicit Shimura reciprocity law in[10](otherwise,this note would not have existed).My approach is very different from his.The last section of this work is inspired by his work.I thank Conrad,B.,Howard,B.,Nicole,M.H.,Rapoport,M.,and Yuan Xinyi for the helpful discussions.This work was done during my visit to Microsoft in Fall 2013 and to the MPIM-Bonn in Spring 2014.I thank both institutes for providing me with the excellent working conditions.Finally,I thank the anonymous referee for his/her careful reading and suggestions/comments on the earlier versions of this paper.

[1]Costello,C.,Deines-Schartz,A.,Lauter,K.and Yang,T.H.,Constructing abelian surfaces for cryptography via Rosenhain invariants,LMS J.Comput.Math.Ser.A,17,2014,157–180.

[2]Genestier,A.and Ngo,B.C.,Lectures on Shimura varieties,Asian-French Summer School on Algebraic Geometry and Number Theory,Volume I,187–236,Panor.Synth.,29,Soc.Math.France,Paris,2009.

[3]Katz,N.and Mazur,B.,Arithmetic moduli of elliptic curves,Ann.Math.Studies,108,Princeton University Press,1985.

[4]Lang,S.,Complex Multiplication,GTM,255,Springer-Verlag,New York,1983.

[5]Shimura,G.,On canonical models of bounded symmetric domains I,Ann.Math.,91,1970,144–222,II,92,1970,528–549.

[6]Shimura,G.,On certain reciprocity laws for theta functions and modular functions,Acta Math.,141,1978,35–71.

[7]Shimura,G.,Abelian Vareities with Complex Multiplication and Modular Forms,Princeton University Press,princeton,1998.

[8]Shimura,G.and Taniyama,Y.,Complext Multiplication of Abelian Varieties and Its Applications to Number Theory,Publ.Math.Soc.Japan,6,The Mathematical Society of Japan,Tokyo,1961.

[9]Silverman,J.H.,Advanced Topics in the Arithmetic of Elliptic Curves,GTM 151,Springer-Verlag,New York,1994.

[10]Streng,M.,An explicit version of Shimura’s reciprocity law for the Siegel modular functions,preprint,2012.