New Quantum MDS Code from Constacyclic Codes∗

Liqin HUQin YUEXiaomeng ZHU

1 Introduction

Quantum codes were introduced to protect quantum information from decoherence and quantum noise.After the pioneering work of Shor[24]and Steane[25],a systematic mathematical scheme has been employed to construct q-ary quantum codes from classical error-correcting codes over Fqor Fq2with certain orthogonality properties.The quantum codes obtained in this way are called stabilizer codes.After the establishment of the connection between quantum codes and classical codes(see[3]),the construction of stabilizer codes can be converted to that of classical codes with symplectic,Euclidean,or Hermitian self-orthogonal property.

A q-ary quantum code Q of length n and size K is a K-dimensional subspace of a qndimensional Hilbert spaceAn important parameter of a quantum code is its minimum distance:If a quantum code has minimum distance d,then it can detect d− 1 and correctquantum errors.Let k=K,we useto denote a q-ary quantum code of length n with size qkand minimum distance d.The parameters of an[[n,k,d]]qquantum code must satisfy the quantum Singleton bound:2d ≤ n−k+2(see[19–20]).A quantum code achieving this quantum Singleton bound is called a quantum maximum-distanceseparable(MDS for short)code.Ketkar et al.in[19]pointed out that,for any odd prime power q,if the classical MDS conjecture holds,then the length of nontrivial quantum MDS codes can not exceed q2+1.As mentioned in[16],except for some sparse lengths n such as n=q2+1,and q2,almost all known q-ary quantum MDS codes have minimum distance less than or equal to+1.The following result gives a connection between classical Hermitian self-orthogonal MDS codes and quantum MDS codes.

Theorem 1.1(see[2])If C is a q2-ary[n,k,n−k+1]MDS code such that C⊆ C⊥H,then there exists a q-ary[[n,n−2k,k+1]]quantum code.

In recent years,constructing quantum MDS codes has become a hot research topic.Many classes of quantum MDS codes have been found by employing different methods(see[1,4–5,7–17,22–23]).Recently,Kai et al.[17–18]constructed several classes of good quantum codes from classical constacyclic codes,including some new classes of quantum MDS codes.

Motivated by the above works,a new family of quantum MDS code is constructed in this paper.The quantum code in this paper can be regarded as a generalization of[18,Theorems 3.14–3.15],in the sense that our quantum MDS code has bigger minimum distance.

2 Preliminaries

In this section,we recall some definitions and basic properties of constacyclic codes.Throughout this paper,q denotes an odd prime power and Fq2denotes the finite field with q2elements.Assume that n is a positive integer relatively prime to q,i.e.,gcd(n,q)=1.

Letbe thevector space of n-tuples.A linear code C of length n is an Fq2subspace ofFor a nonzero element η of Fq2,a linear code C of length n over Fq2is said to be η-constacyclic if(ηcn−1,c0,···,cn−2) ∈ C for every(c0,c1,···,cn−1) ∈ C.If each codeword c=(c0,c1,···,cn−1)∈ C corresponds with its polynomial representation c(x)=c0+c1x+···+cn−1xn−1∈ Fq2[x],then the η-constacyclic code C is identified with exactly one ideal of the quotient ring Fq2[x]/(xn− η).Since Fq2[x]/(xn− η)is a principal ideal ring,an η-constacyclic code C is generated uniquely by a monic divisor g(x)of xn−η and denoted by C=?g(x)?.Hence g(x)and h(x)=are called the generator polynomial and the check polynomial of C,respectively.

Similarly to cyclic codes,there exists the following BCH bound for η-constacyclic codes(see[21]).

Lemma 2.1Let C=?g(x)?be an η-constacyclic code of length n overand gcd(q,n)=1.Suppose that the roots of g(x)include γαi,i=1,2,···,d − 1(≤ degg(x)),where γ and α are nonzero elements in some extension field of Fq2,and α is an element of order n.Then the minimum distance of the code is at least d.

For two vectors b=(b1,b2,···,bn)and c=(c1,c2,···,cn)in,we define the Hermitian inner productto be=where=for each 1≤i≤n.The vectors b and c are called orthogonal with respect to Hermitian inner product if=0.For a q2-ary linear code C,the Hermitian dual codes of C is defined as

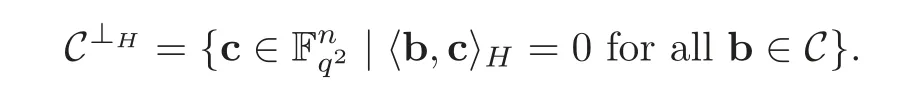
A q2-ary linear code C of length n is called Hermitian self-orthogonal if C⊆ C⊥H.Conversely,if C⊥H⊆ C,we say that C is a Hermitian dual-containing code.

The automorphism of Fq2given by“−”,=aqfor any a∈ Fq2,can be extended to an automorphism of[x]in an obvious way:

for any a0,a1,···,anin,which is also denoted by “ − ” for simplicity.

For a monic polynomial f(x)∈Fq2[x]of degree k with f(0)?0,its reciprocal polynomial will be denoted by

The following result gives the generator polynomial of C⊥H.

Lemma 2.2(see[26,Lemma 2.1(ii)])Let C=?g(x)?be an η-constacyclic code of length n and dimensional k over.Set h(x)=.Then the Hermitian dual code C⊥His an-constacyclic code with the generator polynomialwhere

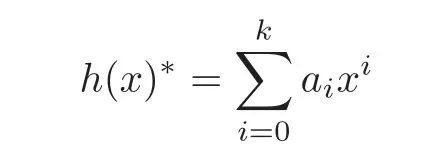
and

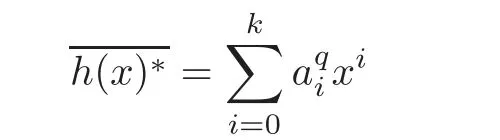
are the reciprocal and conjugate-reciprocal polynomials of h(x),respectively.

By Lemma 2.2,we can get the following result.

Lemma 2.3Let η∈Fq2be a primitive r-th root of unity and let C be a Hermitian dualcontaining η-constacyclic code of length n over Fq2.Then η = η−q,i.e.,r|q+1.

Let C=?g(x)?be an η-constacyclic code of length n and let Ω ={1+jr|0 ≤ j ≤ n− 1}.The set Z={k ∈ Ω |g(ζk)=0}is called the defining set of C,where ζ is a primitive rn-th root of unity in some extension field of Fq2such that ζn= η.The following result presents a criterion to determine whether or not an η-constacyclic code of length n over Fq2is Hermitian dual-containing.

Lemma 2.4(see[18,Lemma 2.2])Let r be a positive divisor of q+1 and let η ∈Fq2 be of order r.Assume that C is an η-constacyclic code of length n over Fq2with a defining set Z.Then C is a Hermitian dual-containing code if and only if Z ∩ (−q)Z= ∅,where(−q)Z={−qz(mod rn)|z∈ Z}.

The Hermitian construction suggests that we can obtain q-ary quantum codes as long as we can construct classical Hermitian dual-containing codes over Fq2.Constacyclic codes form an important class of linear codes due to their good algebraic structures.In this paper,we will use the Hermitian construction to obtain MDS quantum codes through constacyclic codes.

3 New Quantum MDS Code

Throughout this section,we always assume that η is a primitive r-th root of unity in Fq2 with r|(q+1),and n is a positive integer with rn|(q4−1)and rn?(q2−1).In this section,we construct a family of q-ary quantum codes with good parameters through the Hermitian construction.

Let C be an η-constacyclic code and let Ω ={1+jr|0 ≤ j ≤ n−1}.Since rn|(q4−1),we always have that|C1+jr|≤2,0≤j≤n−1,where C1+jris the q2-cyclotomic coset containing 1+jr modulo rn.

Lemma 3.1There exist exactly two q2-cyclotomic cosets C1+rkandwith|C1+rk|=|C1+r(k+n2)|=1 if and only if n|(q2+1)and n is even,where rk−1mod?,0≤k≤−1.

ProofSuppose that i=1+jr∈Ω,0≤j≤n−1.Then there are exactly two q2-cyclotomic cosets Ciand Ci?(i,i?∈ Ω,ii?)with|Ci|=|Ci?|=1 if and only if the congruence equation(1+jr)q2≡1+jr(mod rn)has exactly two different solutions,which implies that

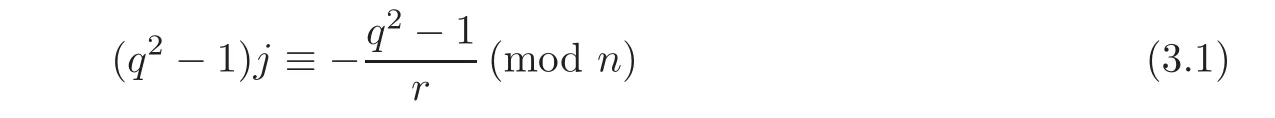
has two solutions k and k?with 0≤k?=k?≤n−1.As rn|q4−1 and gcd(q2−1,q2+1)=2,(3.1)has two solutions if and only if gcd(n,q2−1)=2 if and only if n|(q2+1)and n is even,so i=1+rk,i?=1+r?k+?,where rk≡−1?mod?,0≤k≤−1.

Suppose that n|q2+1 and n is even.By Lemma 3.1,there are exactly two q2-cyclotomic cosets Csandwith|Cs|==1,where s=

Lemma 3.2Let n be an even divisor of q2+1.Suppose that s=.Then Ω={1+jr|0≤j≤n−1}is a disjoint union of q2-cyclotomic cosets:

ProofSince n|q2+1 and n is even,by Lemma 3.1 there are exactly two q2-cyclotomic cosets Csandwith one element.

For each j,1≤j≤−1,

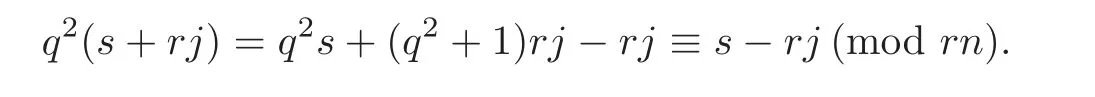
Hence Cs+rj={s−rj,s+rj}for 1≤j≤−1.

In order to use Lemma 3.2 to construct Hermitian dual-containing MDS constacyclic code,we need the condition that−qCs=,i.e.,Cs−qCs.

Proposition 3.1Let n be an even divisor of q2+1 and s=Then Cs?−qCsif and only if 2,where Cs={s}is the q2-cyclotomic coset containing s.

ProofFor s=,s≡−qs(mod rn)if and only if rn|(q+1)s,which implies n|By s=,we have|s with s odd,so n|if and only if 2|.Hence,we get the result.

The following results are given in[18].

Lemma 3.3(see[18,Theorem 3.14])Let q be an odd prime power with the form 20m+3 or 20m+7,where m is a positive integer.Let n=.Then,there exists a q-ary[[n,n−2d+2,d]]-quantum MDS code,where 2≤d≤is even.

Lemma 3.4(see[18,Theorem 3.15])Let q be an odd prime power with the form 20m−3 or 20m−7,where m is a positive integer.Let n=.Then,there exists a q-ary[[n,n−2d+2,d]]-quantum MDS code,where 2≤d≤is even.

Using the Hermitian construction,we will obtain q-ary quantum codes of lengthfrom constacyclic codes over Fq2.The main code of this paper has much larger minimum distance than the one of[18]when q>23.

Let q be an odd prime power with q≡ 3(mod 10)or q≡ −3(mod 10),and n=.We consider η-constacyclic code of length n over Fq2.

In order to construct quantum MDS codes,we give a sufficient condition for η-constacyclic codes which contain their Hermitian duals.For any odd prime power q with q≡±3(mod 10),we first consider the case q≡3(mod 10).

Lemma 3.5Assume that q is an odd prime power with q≡3(mod 10)andodd.Let s=and n=.If C is an η-constacyclic code over Fq2of length n with defining setwhere 0 ≤ δ≤,then C is a Hermitian dual-containing code.

ProofBy Lemma 2.4,it is sufficient to prove that Z∩(−q)Z= ∅.Suppose that Z∩(−q)Z∅.Then,there exist two integers j,k,0≤ j,k ≤,such that s−rj≡ −q(s−rk)(mod rn)or s−rj≡−q(s+rk)(mod rn).

Case Is−rj≡−q(s−rk)(mod rn).This is equivalent to

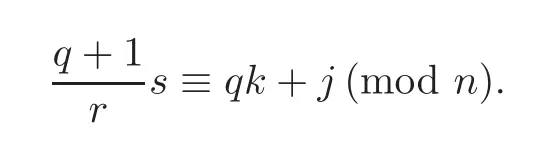
By s=andodd,we obtain

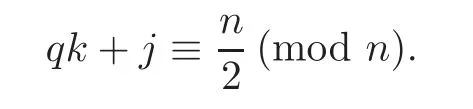
Since 0≤ j,k ≤,0≤ j+qk≤.We have that j+qk≡(mod n)if and only if qk+j=.Since

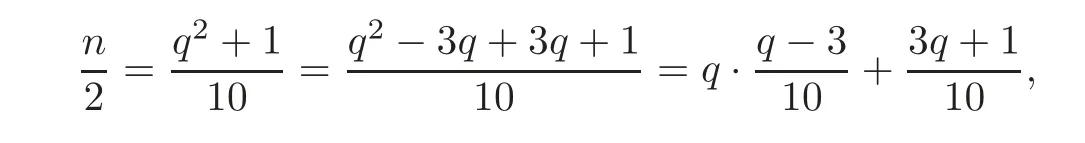
we have

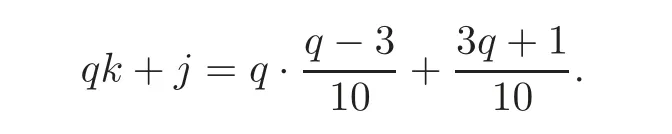
By division algorithm,j=.This is impossible,because

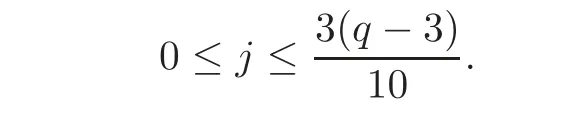
Case IIs−rj≡−q(s+rk)(mod rn).This is equivalent to

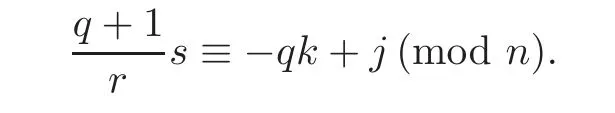
As s=andodd,we obtain

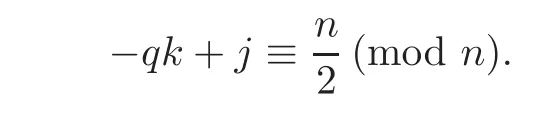
Since 0≤ j,k≤,we have

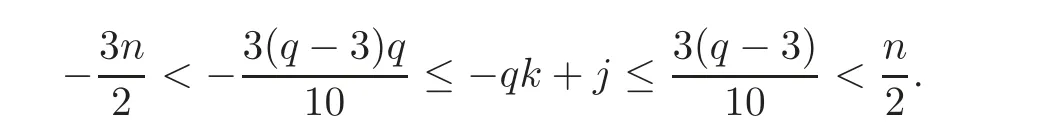
We have that−qk+j≡(mod n)if and only if

Hence

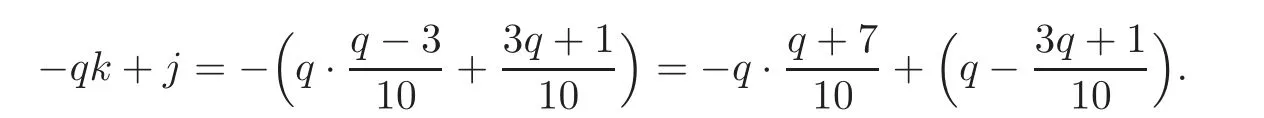
By division algorithm,

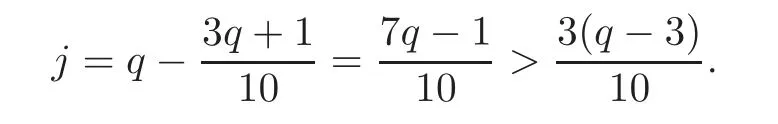
This is impossible.

Theorem 3.1Let q be an odd prime power with q≡3(mod 10).Then,there exist quantum MDS codes with parameterswhereis even.

ProofPut s=withodd.Let η be an r-th primitive root in Fq2.Consider the η-constacyclic code C over Fq2of length n=with defining setwhere 0≤ δ≤From Lemma 3.5,C⊥⊆ C.From Lemma 3.2 we can see that Z contains 2δ+1 consecutive integers.This implies that C has minimum distance at least 2δ+2.Hence,C is an[n,n−2δ−1,2δ+2]MDS constacyclic code.Combining the Hermitian construction with quantum Singleton bound,we can obtain a quantum MDS code with parameterswhere d,2≤d≤,is even.

Compare our quantum MDS codes in Theorem 3.1 with quantum MDS codes in[18],our quantum MDS codes has much bigger minimum distance than the known codes in[18]when q>23,because

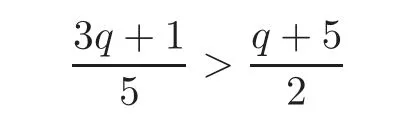
for q>23.

Example 3.1Take q=43,and so n=370.Using Theorem 3.1 produces a new quantum MDS code with parameters[[370,320,26]]43.

For the case q≡ −3(mod 10),we can produce the following quantum MDS codes.The proof is similar to that in the case q≡3(mod 10)and we omit it.

Theorem 3.2Let q be an odd prime power with q≡ −3(mod 10).Then,there exist quantum MDS codes with parameterswhere 2≤ d≤is even.

Example 3.2Take q=37,and so n=137.Using Theorem 3.2 produces a new quantum MDS code with parameters[[137,95,22]]37.

[1]Aly,S.A.,Klappenecker,A.and Sarvepalli,P.K.,On quantum and classical BCH codes,IEEE Trans.Inf.Theory,53(3),2007,1183–1188.

[2]Ashikhmin,A.and Knill,E.,Nonbinary quantum stablizer codes,IEEE Trans.Inf.Theory,47(7),2001,3065–3072.

[3]Calderbank,A.R.,Rains,E.M.,Shor,P.W.and Sloane,N.J.A.,Quantum error correction via codes over GF(4),IEEE Trans.Inf.Theory,44(4),1998,1369–1387.

[4]Chen,H.,Some good quantum error-correcting codes from algebraic-geometric codes,IEEE Trans.Inf.Theory,47(5),2001,2059–2061.

[5]Chen,H.,Ling,S.and Xing,C.,Asymptotically good quantum codes exceeding the Ashikhmin-Litsyn-Tsfasman bound,IEEE Trans.Inf.Theory,47(5),2001,2055–2058.

[6]Chen,H.,Ling,S.and Xing,C.,Quantum codes from concatenated algebraic-geometric codes,IEEE Trans.Inf.Theory,51(8),2005,2915–2920.

[7]Chen,B.,Ling,S.and Zhang,G.,Application of constacyclic codes to quantum MDS codes,IEEE Trans.Inf.Theory,61(3),2015,1474–1484.

[8]Feng,K.,Quantum codes[[6,2,3]]pand[[7,3,3]]p(p≥3)exist,IEEE Trans.Inf.Theory,48(8),2002,2384–2391.

[9]Feng,K.,Ling,S.and Xing,C.,Asymptotic bounds on quantum codes from algebraic geometry codes,IEEE Trans.Inf.Theory,52(3),2006,986–991.

[10]Grassl,M.,Beth,T.and R¨otteler,M.,On optimal quantum codes,Int.J.Quantum Inform.,2(1),2004,757–766.

[11]R¨otteler,M.,Grassl,M.and Beth,T.,On quantum MDS codes,Information Theory,Proceedings International Symposium on IEEE,2004,356.

[12]Guardia,G.G.L.,New quantum MDS codes,IEEE Trans.Inf.Theory,57(8),2011,5551–5554.

[13]Hu,X.,Zhang,G.and Chen,B.,Constructions of new nonbinary quantum codes,Int.J.Theor.Phys.,54(1),2014,92–99.

[14]Jin,L.,Ling,S.,Luo,J.and Xing,C.,Application of classical Hermitian self-orthogonal MDS codes to quantum MDS codes,IEEE Trans.Inf.Theory,56(9),4735–4740,2010.

[15]Jin,L.and Xing,C.,Euclidean and Hermitian self-orthogonal algebraic geometry codes and their application to quantum codes,IEEE Trans.Inf.Theory,58,2012,5484–5489.

[16]Jin,L.and Xing,C.,A construction of new quantum MDS codes,IEEE Trans.Inf.Theory,60,2014,2921–2925.

[17]Kai,X.and Zhu,S.,New quantum MDS codes from negacyclic codes,IEEE Trans.Inf.Theory,59(2),2013,1193–1197.

[18]Kai,X.,Zhu,S.and Li,P.,Constacyclic codes and some new quantum MDS codes,IEEE Trans.Inf.Theory,60(4),2014,2080–2086.

[19]Ketkar,A.,Klappenecker,A.,Kumar,S.and Sarvepalli,P.K.,Nonbinary stabilizer codes over finite fields,IEEE Trans.Inf.Theory,52(11),2006,4892–4914.

[20]Knill,E.and La flamme,R.,Theory of quantum error-correcting codes,Phys.Rev.A,55(2),1997,900–911.

[21]Krishna,A.and Sarwate,D.V.,Pseudocyclic maximum-distance separable codes,IEEE Trans.Inf.Theory,36(4),1990,880–884.

[22]Li,Z.,Xing,L.J.and Wang,X.M.,Quantum generalized Reed-Solomon codes:Unified framework for quantum maximum-distance separable codes,Phys.Rev.A,77,2008,012308(1)–012308(4).

[23]Ling,S.,Luo,L.and Xing,C.,Generalization of Steane’s enlargement construction of quantum codes and applications,IEEE Trans.Inf.Theory,56(8),2010,4080–4084.

[24]Shor,P.W.,Scheme for reducing decoherence in quantum computer memory,Phys.Rev.A,52(4),1995,2493–2496.

[25]Steane,A.M.,Multiple particle interference and quantum error correction,Proc.Roy.Soc.London A,452(1),1996,2551–2577.

[26]Yang,Y.and Cai,W.,On self-dual constacyclic codes over finite fields,Des.,Codes Cryptogr.,74(2),2013,355–364.