On Robustness of Orbit Spaces for Partially Hyperbolic Endomorphisms∗

Lin WANG

1 Introduction

The main aim of this paper is to study the robustness of the orbit structure of a partially hyperbolic endomorphism.Two important properties concerning this subject,the stability property and the shadowing property,are investigated.

It is well-known that structural stability implies that all topological properties of the orbit structure are robust and any Anosov diffeomorphism is structurally stable(see[1]),that is,if f is an Anosov diffeomorphism on a compact manifold M,then any diffeomorphism g C1-close to f is topologically conjugate to f,i.e.,there exists a homeomorphism ϕ on M such that

Moreover,f is also topologically stable(see[20]),that is,for any homeomorphism g C0-close to f,there exists a continuous map ϕ from M onto M such that Equation(1.1)holds.Another important property to characterize the robustness of the orbit structure of a system is the shadowing property.It plays an important role in the investigation of the stability theory(see[14],for example).A well-known result is that an Anosov diffeomorphism f has the shadowing property,that is,for any δ-pseudo-orbit ξ={xk}+∞−∞for f,which satisfies

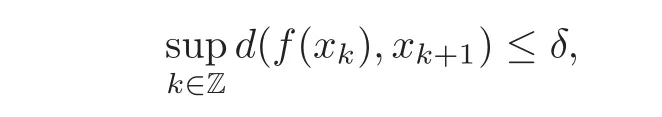
there is a true orbit Orb(x) ε= ε(δ)-tracing(or,say,ε-shadowing)it,i.e.,

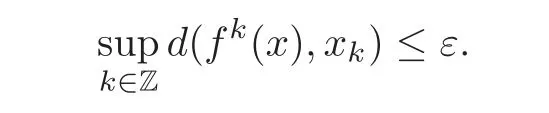
For the non-invertible case,in 1969 Shub[19]showed that expanding maps are structurally stable and share many similar properties as of Anosov diffeomorphisms.At first,people did think that this is also true for any other non-invertible hyperbolic system,the so-called Anosov endomorphisms.In fact,it was not the case.In the 1970s,Ma?né-Pugh[12]and Przytycki[15]found independently some quite different properties for general Anosov endomorphisms.A remarkable result is that except for expanding maps,there is no Anosov endomorphism which is structurally stable.The main reason that makes general Anosov endomorphisms unstable is that the hyperbolicity may be destroyed under small C0perturbations when the negative orbits of some point are not unique.However,when we convert to investigate the robustness of the orbit space(an inverse limit space)which consists of the full orbits of Anosov endomorphisms,we can obtain many interesting results.For example,Liu[10]showed that the dynamical structure of its orbit space is stable with respect to C1perturbations and is semi-stable with respect to C0small perturbations.It is also showed(see[10,22]for example)that the shadowing property holds near the hyperbolic set of any endomorphism.The method of orbit spaces has turned out to be significant in the study of non-invertible dynamical systems(see,for instance,[17–18]for the role this method played in ergodic theory),and it even has some underlying connections with the study of random dynamical systems(see[11]).

The partial hyperbolicity theory was first studied in the work of Brin and Pesin[4]which emerged as an attempt to extend the notion of complete hyperbolicity.A closely related notion of normal hyperbolicity was introduced earlier by Hirsh,Pugh and Shub[5].The ideas and methods in the study of partially hyperbolic dynamical systems extend those in the theory of uniformly hyperbolic dynamical systems,parts of which go well beyond that theory in several aspects.For the general theory of partial hyperbolicity and normal hyperbolicity,we refer to[2–3,5,13].

For a partially hyperbolic diffeomorphism f,we can not expect that the stability and shadowing properties we state above hold because of the existence of the center direction.In[5,13],it was shown that if f has a C1center foliation,then there is a leaf conjugacy between f and its small C1perturbation g,that is,there is a homeomorphism on M which sends center leaves of f to those of g.Recently,Hu and Zhu[6]have shown that any partially hyperbolic diffeomorphism f is quasi-stable in the sense that for any g close to f,an equation similar to(1.1)holds,that is,

in which τ maps points along the center direction.As an application,the continuity of entropy is also obtained for certain partially hyperbolic diffeomorphisms.In[7],Hu,Zhou and Zhu show that any partially hyperbolic diffeomorphism f has the quasi-shadowing property in the sense that for any pseudo-orbit{xk}k∈Z,there is a sequence of points{yk}k∈Ztracing it,in which yk+1is obtained from f(yk)by a motion τ along the center direction.As an application,they gave a version of the spectral decomposition theorem when f has a uniformly compact C1center foliation.We also mention that Kryzhevich and Tikhomirov[9]gave a version of the center shadowing property for partially hyperbolic diffeomorphisms which are dynamically coherent.

In this paper,we shall investigate the robustness of the orbit structure of a partially hyperbolic endomorphism f.There are two main results which can be seen as the generalization of those in[6–7]for the diffeomorphism to the non-invertible case.The first one is that its orbit space is topologically quasi-stable under C0-small perturbations in the following sense:For any covering endomorphism g,there is a continuous map ϕ from MgtoM such that for any{yi}i∈Z∈ ϕ(Mg),yi+1and f(yi)differ only by a motion τ along the center direction.In particular,if f has a C1center foliation,then the above motion τ can be chosen along the center leaves.The second one is that f has the quasi-shadowing property in the following sense:For any pseudo-orbit{xi}i∈Z,there is a sequence of points{yi}i∈Ztracing it in which yi+1is obtained from f(yi)by a motion τ along the center direction.Similarly,we can also choose τ along the center leaves if f has a C1center foliation.We can see that to obtain the quasi-stability and quasi-shadowing properties,they used a unified method which combines the techniques of[8,10,20,22].We also mention that it seems impossible to get a kind of structural quasi-stability for this non-invertible case by using the method in[6],which they used to deal with the invertible case.The main reason is that the technique in[6]depends on the robustness of the center foliation,however,it generally does not hold for the partially hyperbolic endomorphism.

This paper is organized as follows.The statements of results are given in Section 2.We also define some words and notations in the section.In Section 3 we deal with topological quasi-stability,including the proofs of Theorem A and Theorem B.Section 4 is devoted to the quasi-shadowing property,including a sketch of the proof of Theorem C.

2 definitions,Notations and Statements of Results

Let M be an m-dimensional C∞compact Riemannian manifold.We denote by?·?and d(·,·)the norm on TM and the metric on M induced by the Riemannian metric,respectively.Letbe the bi-in finite product of copies of M and endow it with the metric

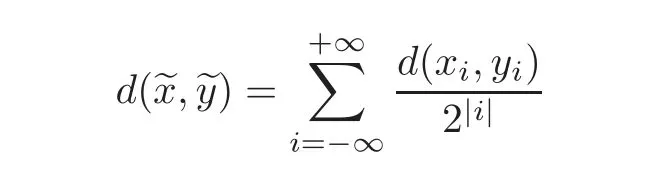
for={xi}i∈Z,={yi}i∈Z∈,which makesa compact metric space.By

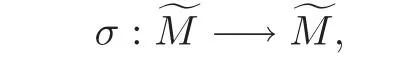
we denote the left shift operator on,and

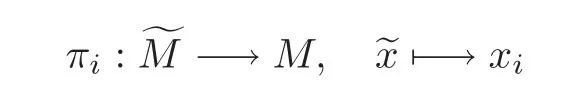
the natural i-th projection for any i∈Z.

Let C0(M,M)be the space of continuous maps on M endowed with the metric

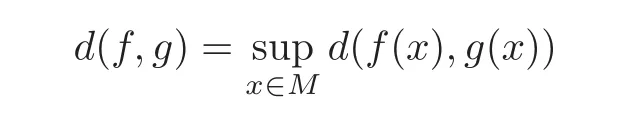
for f,g∈C0(M,M).For any f∈C0(M,M),define

and call it the orbit space or the inverse limit space of f.It is clearly a closed subset of?M.

definition 2.1Assume that f,g ∈ C0(M,M).Let Λ and Δ be,respectively,an invariant set of f and g,and let ϕ :Λf→ Δgbe a continuous map.The map ϕ is called an orbit-space conjugacy if it is a homeomorphism and satisfies

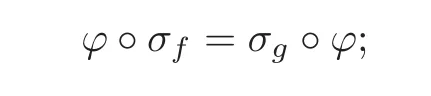
ϕ is called an orbit-space semi-conjugacy if it is surjective and satisfies the preceding equation.

A map f in C0(M,M)is called a covering endomorphism of M if it is a local homeomorphism around every x∈M.By CE0(M)we denote the set of all covering endomorphisms of M.

An endomorphism f∈Endo1(M)∩CE0(M)(where Endo1(M)is the set of C1endomorphisms of M)is an Anosov endomorphism(see[15])if there exists a constant λ with 0< λ <1,and an invariant decomposition TxM=⊕,∀x∈M,such that for any n≥0,

hold for some number C>0.

Assume that f∈C1(M,M)is an Anosov endomorphism.Then there exists a neighborhood U of f in C1(M,M)and numbers δ0>0,such that ∀g ∈ U has the shadowing property(see[10]),that is,for any ε>0,there exists 0< δ< δ0and any δ-pseudo-orbit of g that lies in M can be ε-shadowed by an orbit of g.

We have known that a non-invertible endomorphism on a compact manifold is in general not stable except when it is expanding(see[15–16,21]).However,for an Anosov endomorphism,the dynamical structure of its orbit space(an inverse limit space)is stable with respect to C1-small perturbations and is semi-stable with respect to C0-small perturbations.

Let f be an Anosov endomorphism on M,then f is weakly structurally stable(the dynamical structure of its orbit space is stable with respect to C1-small perturbations)in the following sense:There is ε0>0 and for any 0< ε< ε0,one can find a neighborhood U of f in C1(M,M)such that for any g∈U,there is a unique orbit-space conjugacy ϕ:Mg→Mfsatisfying d(,ϕ())< ε for all∈ Mg(see[10]for example).

Let f be an Anosov endomorphism on M,then f is weakly topologically stable(the dynamical structure of its orbit space is semi-stable with respect to C0-small perturbations)in the following sense:Given ε>0,one can find a neighborhood U of f in CE0(M)such that for any g ∈ U there is an orbit-space semi-conjugacy ϕ :Mg→ Mfsatisfying d(,ϕ())< ε for all∈Mg(see[10]for example).

As is mentioned in the introduction,for any partially hyperbolic system,we cannot expect that the shadowing property holds in general since in this case a center direction is allowed in addition to the hyperbolic directions.Therefore,how to find an analogous property is interesting.

Now,we introduce the definition of partially hyperbolic endomorphisms.

definition 2.2An endomorphism f∈Endor(M)∩CE0(M)(where Endor(M)is the set of Crendomorphisms of M,1≤r≤∞)is said to be(uniformly)partially hyperbolic if there exist numbers λ, λ?, μ and μ?with 0< λ <1< μ and λ < λ?≤ μ?< μ,and an invariant decomposition TxM=Esx⊕⊕E,∀x∈M,such that for any n≥0,

hold for some number C>0.

andare called stable,center and unstable subspaces,respectively.Via a change of the Riemannian metric,we always assume that C=1.Moreover,for simplicity of notation,we assume that λ=

In the following,we always assume that f is a partially hyperbolic endomorphism as mentioned above and g is a covering endomorphism C0-close to f.

Denote by(resp.,t=s,c,u)the restriction of the pull-back bundle(TM)(resp.(Et),t=s,c,u)via the projection π0:−→M to the orbit space Mgof g.We will identify(resp.,t=s,c,u)with Tπ0(?x)M(resp.,t=s,c,u)via the obvious isomorphism.Let Γ = Γ(Mg)be the Banach space of all continuous sections ofwith the norm

Similarly,we denote by Γs,Γcand Γuthe spaces of continuous sections of,andrespectively.Also,we denote Γus= Γu⊕ Γs.Let:→be the projection ontoalong.It is obvious thatis actually the projectionandare defined in a similar way.

Since M is compact and f is locally homeomorphic,we can take the constant ρ0>0 such that for any x∈M,the standard exponential mapping expx:{v∈TxM:?v?<ρ0}→M and the restriction of f to B(x,ρ0)are all diffeomorphisms to the image.Clearly,we have d(x,expxv)=?v?for v ∈ TxM with?v?< ρ0.Takesuch that for any x,y∈M,any z∈f−1(x)with d(z,y)≤ρ,v∈TyM with?v?≤ρ,

Decrease ρ if necessary,such that both sides of equations(3.3)and(3.17),in the proofs of Theorem A and Theorem B respectively,are contained in the set{v∈TxM:?v?<ρ0}.

For any given continuous center section u∈Γcwith?u?<ρ and∈Mg,we define a family of smooth mapson B(π0(),ρ)by

Theorem ALet f be a partially hyperbolic endomorphism.Then f is topological quasistable in the following sense:For any ε∈ (0,ρ),there exists δ>0 such that for any g ∈CE0(M)with d(f,g)< δ,there exists a continuous center section u ∈ Γcand a continuous map ϕ:Mg→such that for any∈Mg,

in which

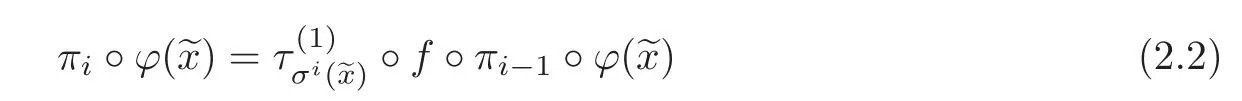
for any i∈Z.

Moreover,u and ϕ can be chosen uniquely so as to satisfy the following conditions:

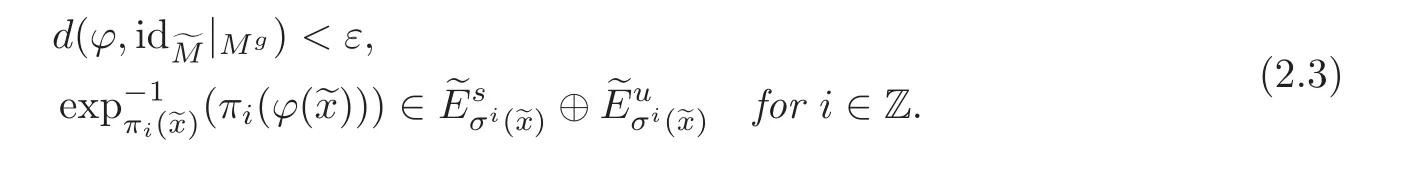
It is well-known that if f is a partially hyperbolic diffeomorphism,then there always exist stable and unstable foliations,but the existence of center foliation is a rather delicate matter and is known under several rather stringent assumptions(see Chapter 5 of[13]for the details).When f is a partially hyperbolic endomorphism,the existence of these invariant foliations is more subtle since the invariant manifolds rely on the whole orbits of the system but the negative orbits of a point are not uniquely determined under the endomorphism.However,we can see that for the systems in the following example,these invariant foliations exist,in particular,the center foliation is even smooth.

Example 2.1Let N be a smooth closed Riemannian manifold,h:N −→N an Anosov endomorphism.Then

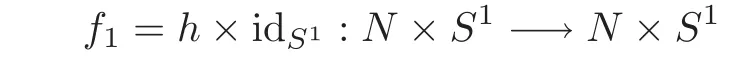
and

are all partially hyperbolic endomorphisms,where R is a rotation on the unit circle S1.

If f has C1center foliation,then we can require τ in Theorem A to move along the center foliation.In this case,for any ε>0 and∈ Mg,we denotewhereis the ε-ball in⊕Obviously,is a smooth disk transversal toatSince the center foliationis C1,we can conclude that if y is close enough to π0(),then there is a locally defined mapon some neighborhood U(π0())of π0()and a constant K1>1 which is independent ofsuch that for any y ∈ U(π0()),we have

and

Theorem BLet f be a partially hyperbolic endomorphism with a C1center foliationThen f is topological quasi-stable in the following sense:For any ε∈ (0,ρ),there exists δ>0 such that for any g∈ CE0(M)with d(f,g)<δ,there exists a continuous map ϕ:Mg→such that for any∈Mg,

in which

for any i∈Z.

Moreover,ϕ can be chosen uniquely so as to satisfy the conditions in(2.3).

In the following,we will apply the unified method we used in Theorem A and Theorem B to study the so-called quasi-shadowing property for a partially hyperbolic endomorphism f.For a sequence of points{xk}k∈Zand a sequence of vectors{uk∈}k∈Zwith?uk?< ρ for any k ∈ Z,we define a family of smooth maps=(·,uk)on B(xk,ρ),k ∈ Z,by

Theorem CLet f be a partially hyperbolic endomorphism.Then f has the quasi-shadowing property in the following sense:For any ε∈ (0,ρ),there exists δ>0 such that for any δ-pseudoorbit{xk}k∈Zof f,there exists{yk}k∈Zand a sequence of vectors{uk∈ Ecxk}k∈Zsuch that

where

Moreover,{yk}k∈Zand{uk}k∈Zcan be chosen uniquely so as to satisfy

If f has C1center foliation,then we can require τ in Theorem C to move along the center foliation.In this case,for any ε>0,we denote Σε(x)=expx(Hx(ε)),where Hx(ε)is the ε-ball in⊕,andis the locally defined map on some neighborhood U(x)of x satisfying that for any y∈U(x),

and

for the constant K1>1.

Theorem DLet f be a partially hyperbolic endomorphism with C1center foliationThen f has the quasi-shadowing property in the following sense:For any ε∈ (0,ρ),there exists δ>0 such that for any δ-pseudo-orbit{xk}k∈Zof f,there exists a sequence of points{yk}k∈Zsuch that

where

Moreover,{yk}k∈Zcan be chosen uniquely so as to satisfy(2.10).

3 Topological Quasi-stability

Recall that?·?is the norm on TM.We define the norm?·?1on TM by?w?1=?u?+?v?if w=u+v∈TxM with u∈and v∈⊕Similarly,if w=u+v∈Γ with u∈Γcand v∈Γus,we also define?w?1=?u?+?v?.By the triangle inequality and the fact that the angles between Ecand Eu⊕Esare uniformly bounded away from zero,we know that there exists a constant L such that

For any ε>0,we denote

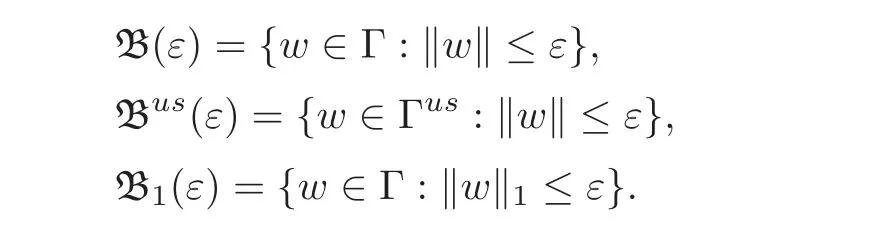
3.1 The general case

Proof of Theorem ATo find a continuous center section u∈Γcand a continuous map ϕ :Mg→satisfying(2.1)and the conditions in(2.2)–(2.3)of this theorem,we shall first try to solve the equation

which satisfies(2.2)–(2.3)for unknown u and ϕ.

Let={xi}i∈Z∈ Mg.Putting πi◦ ϕ()=expxi(v(σi()))for v ∈ Bus(ρ)and i∈ Z,we see that(3.2)is equivalent to

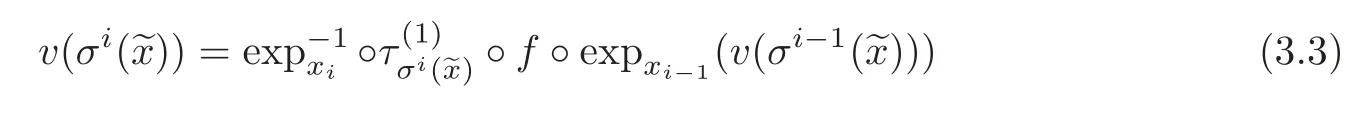
for any i∈Z.

By the definition ofwe have

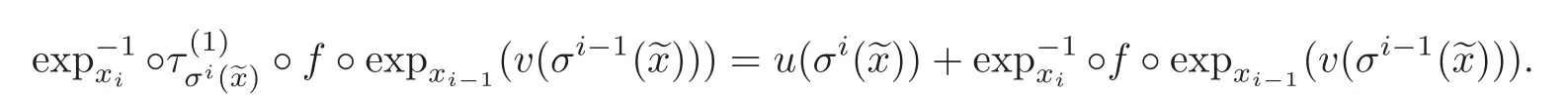
define an operator β :B(ρ)→ Γ and a linear operator F:Γ → Γ by

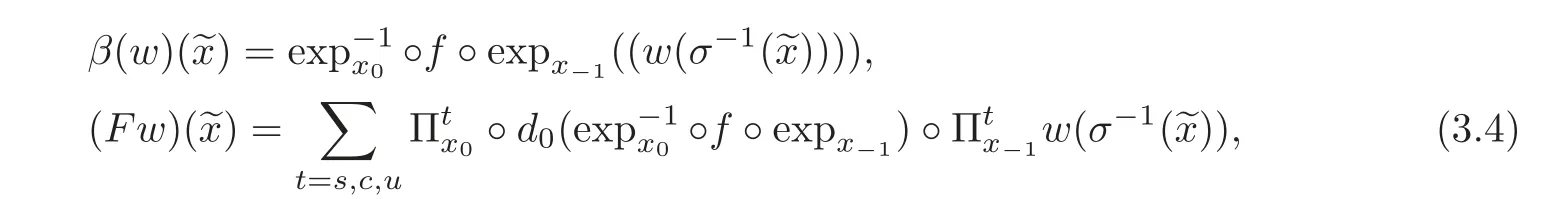
respectively.

Let

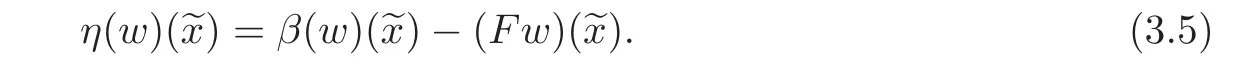
Therefore,by(3.4)–(3.5),(3.3)is equivalent to

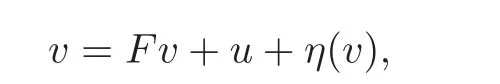
and is further equivalent to

define a linear operator P from a neighborhood of 0∈ Γ to Γ by

for ω =u+v∈ Γ,where u ∈ Γcand v∈ Γus.

define an operator Φ from a neighborhood of 0 ∈ Γ to Γ by

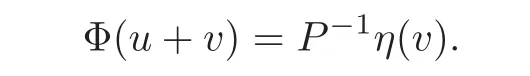
Hence,Equation(3.2)is equivalent to

namely,u+v is a fixed point of Φ.

We will prove that for any ε∈ (0,ρ),there exists δ= δ(ε)such that for any g ∈ CE(M)with d(f,g) ≤ δ,Φ :B1(ε)→ B1(ε)is a contracting map,and therefore has a fixed point in B1(ε).Hence,(3.2)has a unique solution.

Recall that λ is the hyperbolic constant of the partially hyperbolic endomorphism f on M.Let∈(λ,1)be given.We can find

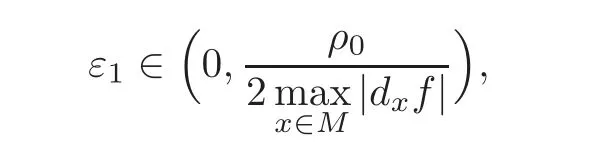
such that for any ε∈ (0,ε1),there exists

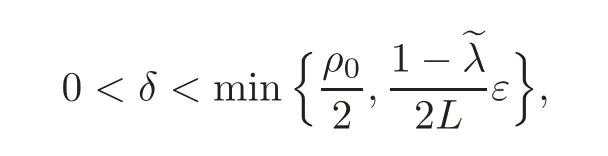
which ensures that for any d(f(y),x)<δ,the following claims hold.

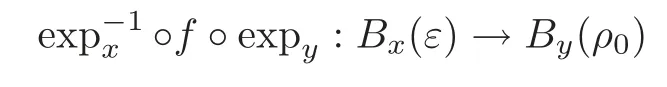
(1)The map(here Bx(ε)={v ∈ TxM:|v|≤ ε}and By(ρ0)={v ∈ TyM:|v|≤ ρ0})is well defined,since for any v in Bx(ε),

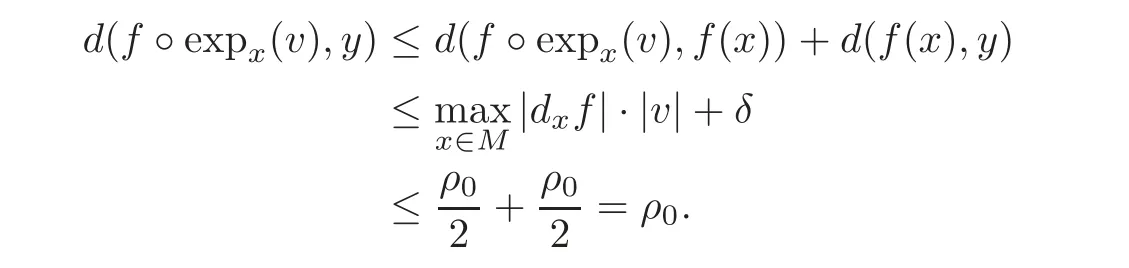
(2)

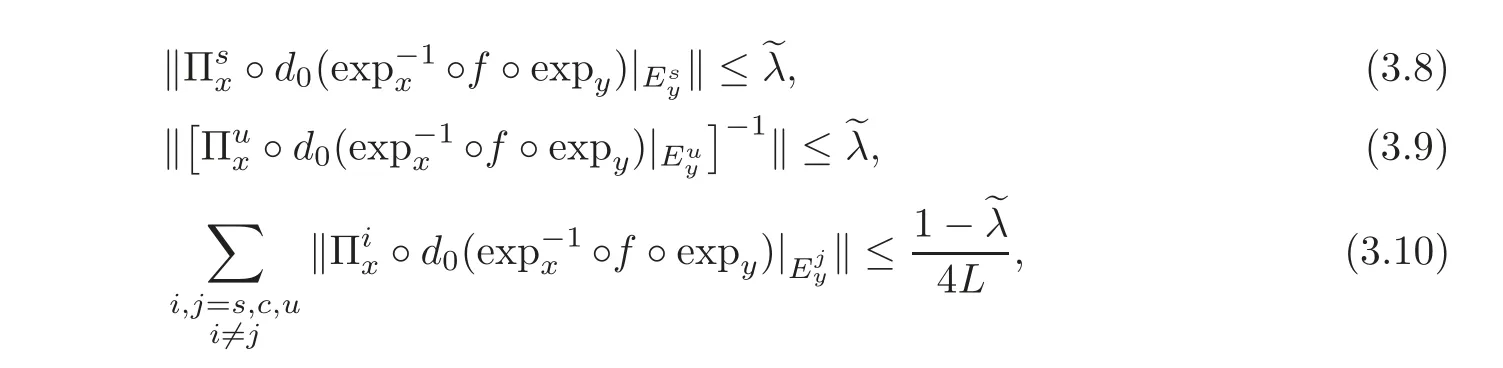
and for any v?,v??∈ Hx(ε)and any t∈ [0,1],

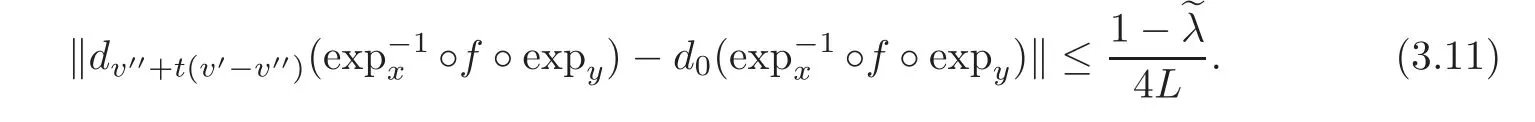
We will prove that Φ :B1(ε)→ B1(ε)is a contracting map in the following steps.

Step 1For δ>0 satisfying(3.8)–(3.11)and for any v,v?∈ Bus(ε),

By the definition of η,we can write it in a neighborhood of 0 ∈ Γus:

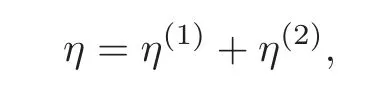
where

and

for={xi}i∈Z∈ Mg.Note that for v?,v??∈ Bus(ε),we have

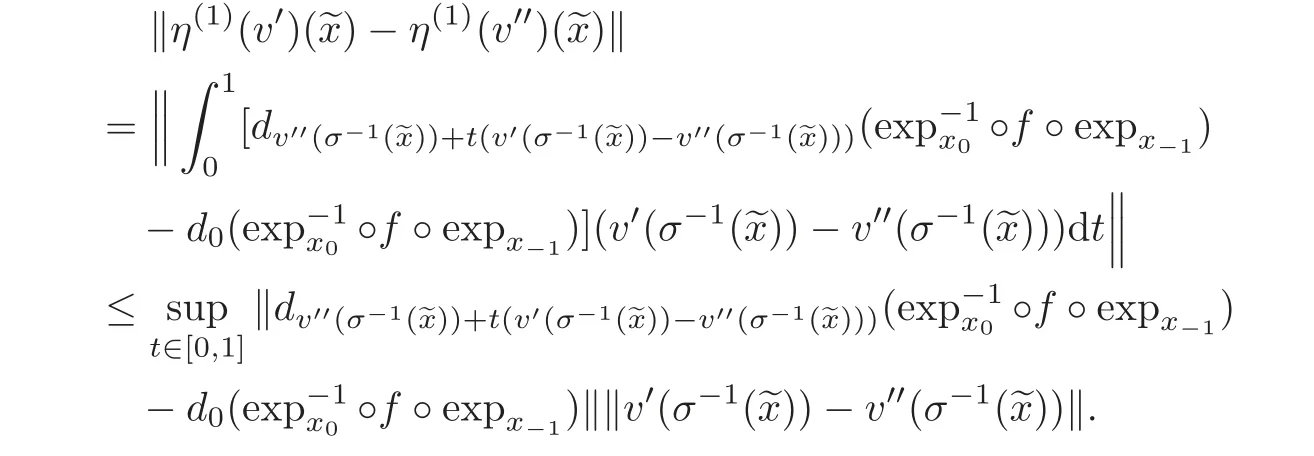
Therefore,from(3.11)we have

By(3.10),we have,for v?,v??∈ Bus(ε),

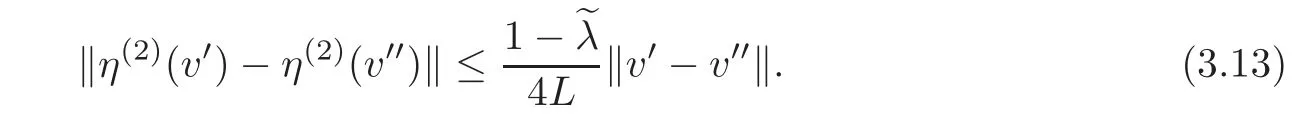
Combining(3.12)–(3.13),for v?,v??∈ Bus(ε),we have

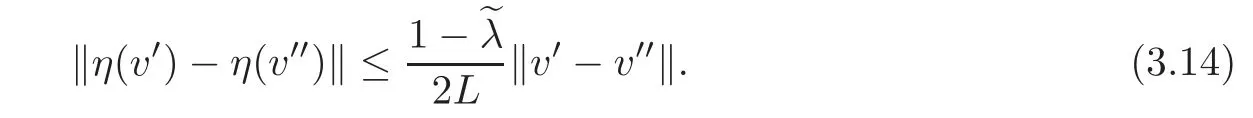
Hence,we can get the result we need immediately.

Step 2For any δ>0 satisfying(3.8)–(3.11)and any g ∈ CE(M)with d(f,g) ≤ δ,the operator P defined as(3.6)is invertible and

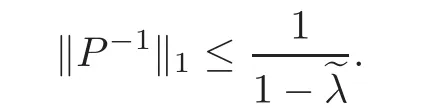
By the definition of P,we have P|Γc=idΓcand P|Γt=idΓt − Ft,t=s,u,where the operators Ft:Γ → Γ,t=s,u,are defined by

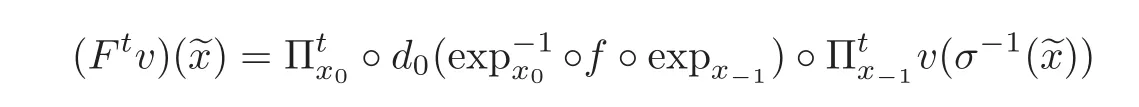
for v∈ Γsu.So P(Γt)= Γi,t=u,s,c.

By(3.8)–(3.9),?Fs?.?(Fu)−1?≤<1.Hence,both P|Γsand P|Γuare invertible and

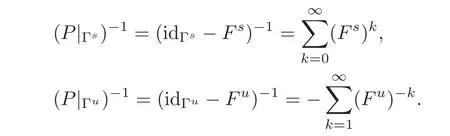
It follows that

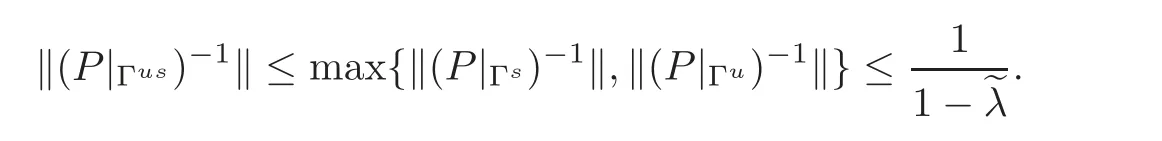
It is obvious that

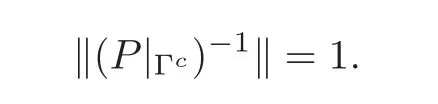
So we obtain that

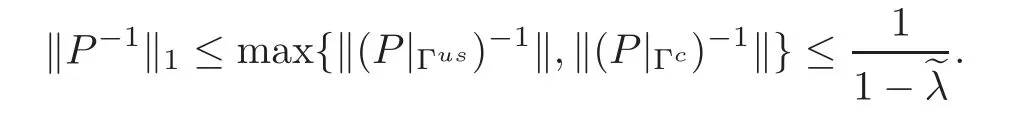
This is what we need.

Step 3For any ε∈ (0,ε1),there exists δ= δ(ε)>0 such that for any g ∈ CE(M)with d(f,g)≤ δ,Φ(B1(ε))⊂ B1(ε)and for any ω,ω?∈ B1(ε),

For any ε∈ (0,ε1),take δ∈ (0,min)such that(3.8)–(3.11)hold.

By step 2 above,we have

Take w=u+v∈ B1(ε)with u ∈ Γcand v∈ Γus.By(3.15)and the step 1,we can get

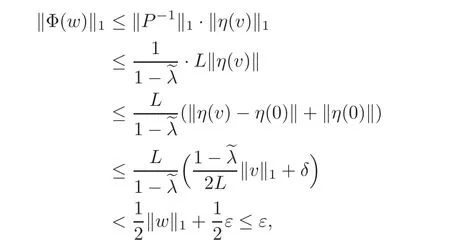
which implies that Φ(B1(ε)) ⊂ B1(ε).

Similarly,for two elements w=u+v,w?=u?+v?∈ B1(ε)with u,u?∈ Γcand v,v?∈ Γus,we have

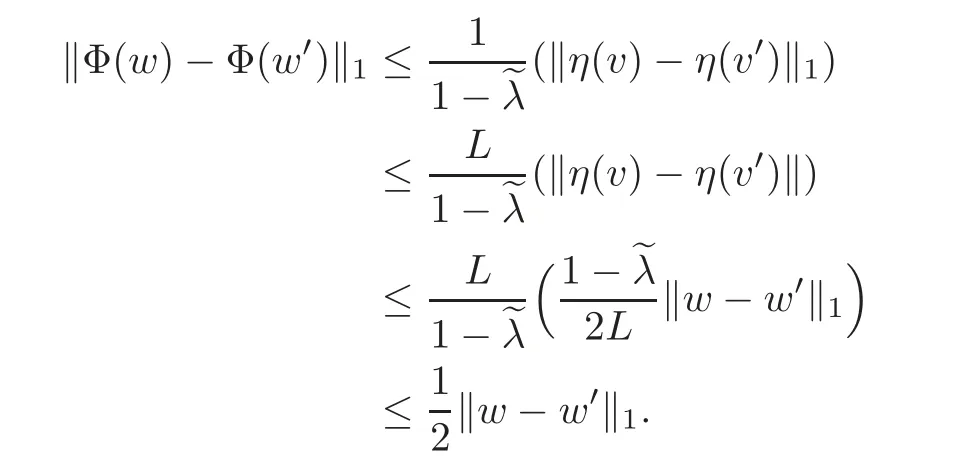
This proves that Φ :B1(ε)→ B1(ε)is a contracting map.

3.2 The center foliation is C1

Proof of Theorem BThe proof is similar to that of Theorem A.

To find a continuous map ϕ:Mg→satisfying(2.1)and the conditions in(2.7)and(2.3)of this theorem,we shall first try to solve the equation

which satisfies(2.3)and(2.7)for unknown ϕ.

Let={xi}i∈Z∈ Mg.Putting πi◦ ϕ()=expxi(v(σi()))for v ∈ Bus(ρ)and i∈ Z,we see that(3.16)is equivalent to

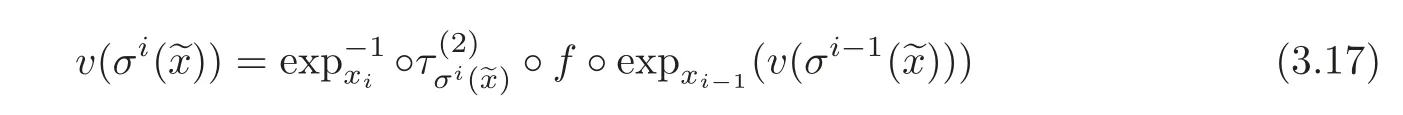
for any i∈Z.

define an operator β :Bus(ρ)→ Γusand a linear operator F:Γus→ Γusby

Let

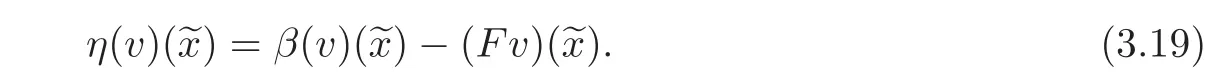
Therefore,by(3.18)–(3.19),(3.17)is equivalent to

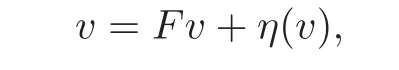
and is further equivalent to

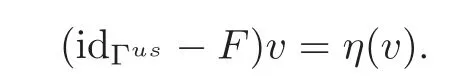
define a linear operator P from a neighborhood of 0 ∈ Γusto Γusby

for v∈ Γus.

define an operator Φ from a neighborhood of 0 ∈ Γusto Γusby

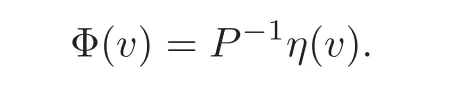
Hence,the equation(3.2)is equivalent to

namely,v is a fixed point of Φ.

The remaining work is to show that for any ε∈ (0,ρ),there exists δ= δ(ε)such that for any g ∈ CE0(M)with d(g,f)≤ δ,Φ :Bus(ε)→ Bus(ε)is a contracting map,and therefore has a fixed point in Bus(ε).Hence,(3.16)has a unique solution.To this end,we only need to slightly modify the proof of Theorem A.

4 Quasi-shadowing Property

As we mentioned above,the proofs of Theorem C and Theorem D follow essentially the ideas presented in the proofs of Theorem A and Theorem B,respectively.Instead of applying the contraction principle for the operator built on the space of continuous sections of the bundle on the whole orbit spaces,we now only need to do the similar work for the operator built on the space of continuous sections of the bundle on a single pseudo-orbit.So we will only modify the notations to the new settings and give a sketch of the proof of Theorem C.

For any sequence{xk}k∈Z,denote

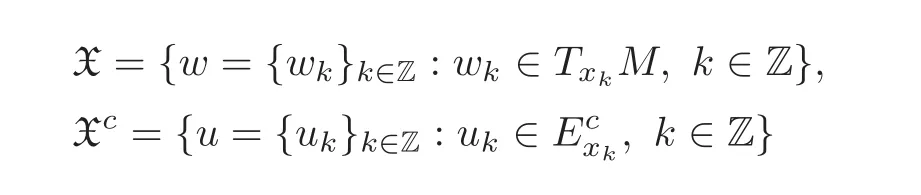
and

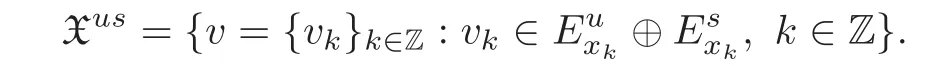
For any

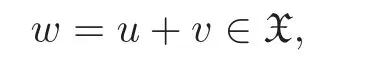
where u∈Xcand v∈Xus,we also define

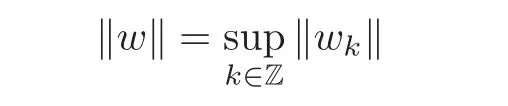
and

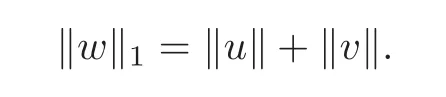
For any ε>0,we denote

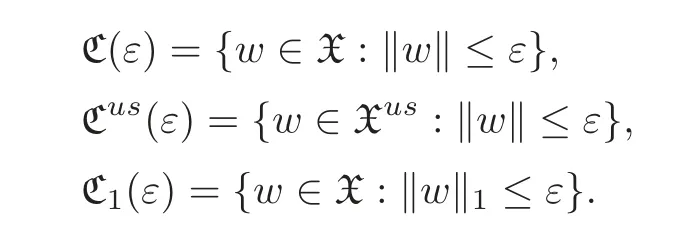
A sketch of the proof of Theorem CGiven a δ-pseudo-orbit{xk}k∈Zof f,to find a sequence of points{yk}k∈Zand a sequence of vectors{uk∈}k∈Zsatisfying(2.8)–(2.10),we shall try to solve the equation

for unknown{yk}k∈Zand{uk∈}k∈Z.Putting

then the equation(4.1)is equivalent to

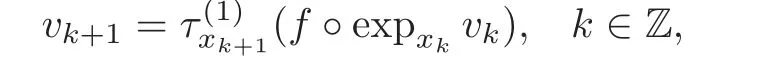
i.e,

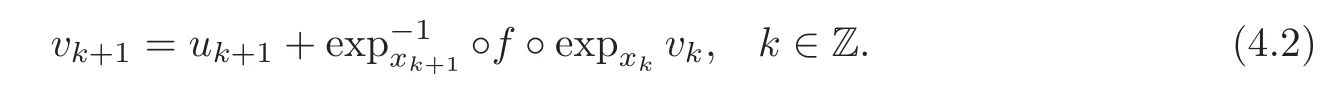
define an operator β :Cus(ρ)→ X and a linear operator A:Cus(ρ)→ Xusby

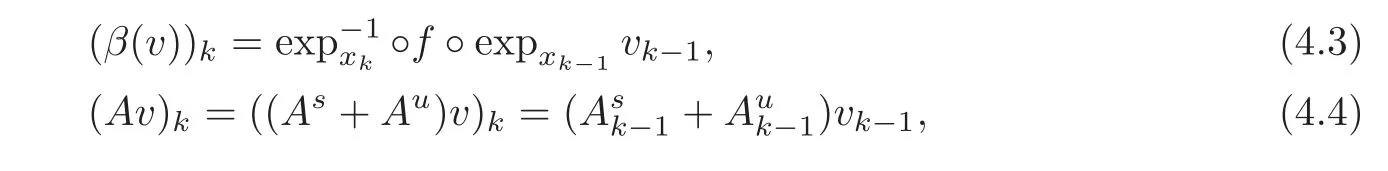
where

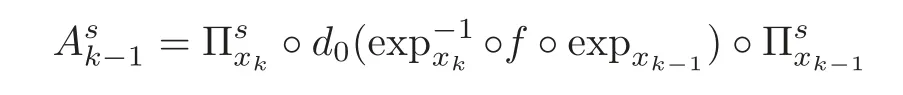
and

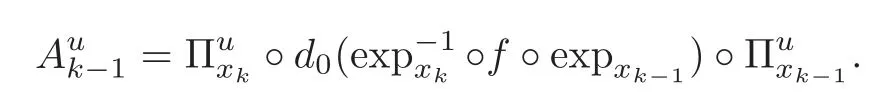
Let the operator

and then by(4.3)–(4.4),(4.2)is equivalent to

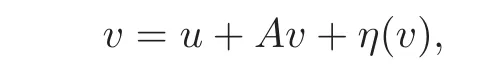
and is further equivalent to

define a linear operator P from a neighborhood of 0∈X to X by

for w=u+v∈X,where u∈Xcand v∈Xus.

define an operator Φ from a neighborhood of 0 ∈ X to X by

for w=u+v in a neighborhood of 0∈X,where u∈Xcand v∈Xus.Hence,Equation(4.2)is equivalent to

namely,w is a fixed point of Φ.

The remaining work is to show that for any ε∈ (0,ρ),there exists δ= δ(ε)such that for a δ-pseudo-orbit{xk}k∈Zof f,Φ :Cus(ε) → Cus(ε)is a contracting map,and therefore has a fixed point in Cus(ε).It is almost a verbatim proof of Theorem A.

AcknowledgementI would like to thank Professor Zhu Yujun for the helpful discussion and suggestions.

[1]Anosov,D.,Geodesic flows on closed Riemann manifolds with negative curvature,Proc.Steklov Inst.Math.,90,1967,3–210.

[2]Barreira,L.and Pesin,Y.,Nonuniform Hyperbolicity,Cambridge University Press,Cambridge,2007.

[3]Bonatti,C.,Diaz,L.and Viana,M.,Dynamics Beyond Uniform Hyperbolicity:A Global Geometric and Probabilistic Perspective,Encyclopaedia Math.Sci.,102,Springer-Verlag,Berlin,2005.

[4]Brin,M.and Pesin,Y.,Partially hyperbolic dynamical systems,MAth.USSR-Izv.,8,1974,177–218.

[5]Hirsch,M.,Pugh,C.and Shub,M.,Invariant Manifolds,Lect.Notes in Math.,Vol.583,Springer-Verlag,Berlin,1977.

[6]Hu,H.and Zhu,Y.,Quasi-stability of partially hyperbolic diffeomorphisms,Tran.Amer.Math.Soc.,366(7),2014,3787–3804.

[7]Hu,H.,Zhou,Y.and Zhu,Y.,Quasi-shadowing for partially hyperbolic diffeomorphisms,Ergodic Theory Dynam.Systems,35,2015,412–430.

[8]Kato,K.and Morimoto,A.,Topological stability of Anosov flows and their centerizers,Topology,12,1973,255–273.

[9]Kryzhevich,S.and Tikhomirov,S.,Partial hyperbolicity and central shadowing,Discrete Contin.Dyn.Syst.,33,2013,2901–2909.

[10]Liu,P.,Stability of orbit spaces of endomorphisms,Manuscripta Math.,93(1),1997,109–128.

[11]Liu,P.and Qian,M.,Smooth Ergodic Theory of Random Dynamical Systems,Lect.Notes in Math.,Vol.1606,Springer-Verlag,Berlin,1995.

[12]Ma,R.and Pugh,C.,Stability of Endomorphisms,Lect.Notes in Math.,Vol.468,Springer-Verlag,Berlin,1974,175–184.

[13]Pesin,Y.,Lectures on Partial Hyperbolicity and Stable Ergodicity,Zurich Lectures in Advanced Mathematics.European Mathematical Society,Zurich,2004.

[14]Pilyugin,S.Y.,Shadowing in Dynamical Systems,Lect.Notes in Math.,Vol.1706,Springer-Verlag,Berlin,1999.

[15]Przytycki,F.,Anosov endomorphisms,Studia Math.,58,1976,249–285.

[16]Przytycki,F.,Ω-stability and structural stability of endomorphisms,Studia Math.,60,1977,61–77.

[17]Pugh,C.and Shub,M.,Ergodic attractors,Trans.Amer.Math.Society,312,1989,1–54.

[18]Qian,M.,Xie,J.and Zhu,S.,Smooth Ergodic Theory for Endomorphisms,Lect.Notes in Math.,Vol.1978,Springer-Verlag,Berlin,2009.

[19]Shub,M.,Endomorphisms of compact differentiable manifolds,Amer.J.Math.,91,1969,171–199.

[20]Walters,P.,Anosov diffeomorphisms are topologically stable,Topology,9,1970,71–78.

[21]Yang,S.L.,More-to-one hyperbolic endomorphisms and hyperbolic sets,Acta Mathematica Sinica,3,1986,420–427.

[22]Zhu,Y.,Zhang,J.and He,L.,Shadowing and inverse shadowing for C1endomorphisms,Acta Mathematica Sinica,22(5),2006,1321–1328.