基于改良圈算法与线性规划的全国自驾游线路优化研究

谢　飞， 杨　扬， 何　杰

(1.西南交通大学 信息科学与技术学院，成都 611756;2.西南交通大学 土木工程学院，成都 611756)



基于改良圈算法与线性规划的全国自驾游线路优化研究

谢飞1， 杨扬1， 何杰2

(1.西南交通大学 信息科学与技术学院，成都 611756;2.西南交通大学 土木工程学院，成都 611756)

摘要：自驾游以自由与个性化、灵活与舒适性等特点深受广大旅游爱好者喜爱，而其线路规划质量直接影响自驾游者的满意度。以全国5A级旅游景区为目的地，选取了一名西安市自驾游爱好者为研究对象，最初运用改良圈算法规划出各省份的游览线路，然后分别以时间最优和费用最优为目标函数，以年旅游时间限值、单次旅游时间限值为约束条件，建立了整数线性规划模型；采用LINGO软件，求解出一条全国5A级景区的自驾游最优方案，具有一定的适用性。

关键词：TSP问题;自驾游;线性规划;改良圈算法; LINGO

近年来，随着我国国民经济的不断发展，越来越多的人选择自驾车出游。自驾游作为一种寓健康、娱乐、休闲于一体，充满个性化和无穷魅力的旅游活动，更能适应现代自助旅游的发展趋势。但是自驾游存在一些劣势，如道路收费太多，无法享受团队优惠，高昂的油费等，使得现阶段自驾游所需费用一直居高不下[1]。制定一个合理的自驾出游路线，不仅可以节约出游时间，提高旅游质量，更能节省旅游成本。此处研究对象是一名西安市的自驾游爱好者，研究内容是以全国5A级旅游景区作为该爱好者的目的地，规划其未来在最短时间内游览完所有5A级景区的旅游路线。在此基础上，进一步考虑出行次数与时间限制、旅游费用等对线路规划的影响，最终设计出费用最优的旅游线路。

自驾游线路优化问题，属于典型的旅行商问题(Traveling Salesman Problem，简称TSP问题)，目前国内外有不少的学者对此做了大量的研究。TSP问题是游客由某地出发，途中恰好不重复地游览完所有景点，然后回到出发地，形成一个闭合的周游型旅游线路[2]。TSP问题的求解方法主要有线性规划法[3]、分支定界法[4]、改良圈算法[5]、遗传算法[6]和蚁群算法[7]等。此处采用整数线性规划模型对TSP问题进行建模求解[13]，但直接建立整数线性规划模型求解，由于设定变量太多而造成运算效率低下，极有可能求不出最优解。卢欣和李衍达[14]通过将问题划分为多层，使每个层次的问题规模限制在一定范围内，以降低问题的复杂度。为此，将自驾游线路规划问题拆分为两个层次求解：各省份游览线路最优问题；全国游览线路最优问题。利用改良圈算法先解决各省份的游览最优线路，再建立以各省份为目的地的整数线性规划模型，最后给出全国5A景区的具体游览方案。

1建模方法理论研究

1.1改良圈算法

结合图论知识，针对每个省份的5A景点，构造一个赋权完全图G=(v,e)，顶点v表示要游览的景点，边e表示连通各景点的道路，边上的权表示景点间的距离。各省份最佳游览线路问题是要在图G中求解出一个权值最小的Hamilton圈，这种圈被称为最优圈。求解最优圈的思路是：先求出一个Hamilton圈C，然后修改C得到具有较小权的另一个Hamilton圈，最终反复修改得到最优圈，这种修改的方法叫做改良圈算法。按照以上思路，先用最邻近算法求解近似最优圈[4]，具体步骤如下：

(i) 选取任意一个顶点v0作为起点，找一条与v0关联且权最小的边e1，e1的另一个端点记作v1，得到一条路v0v1；

(ii) 假设已选出路v0v1…vi，在现有路径中找到一个与vi最邻近的顶点vi+1得到v0v1…vivi+1；

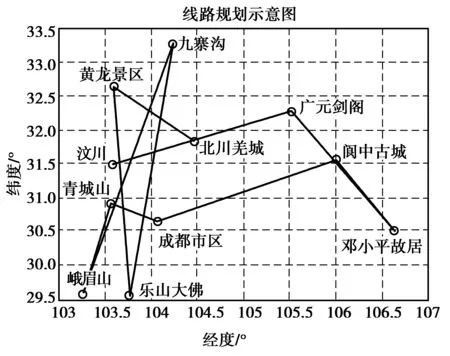
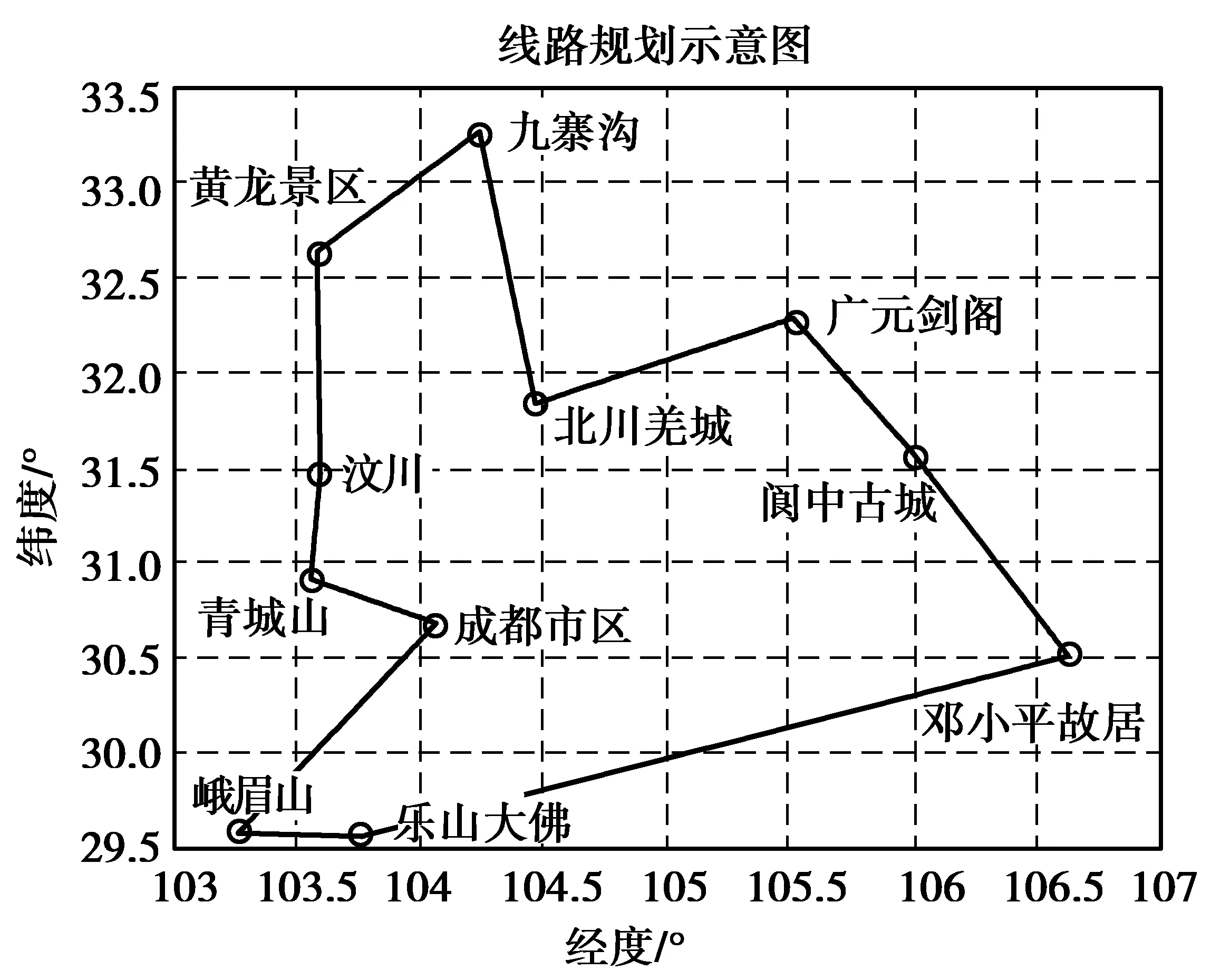
(iii) 若i+1

于是得到了一个近似最优圈，但最邻近算法求得的Hamilton圈一般不是最优解，在此基础上，继续通过改良圈算法，便可获得更短的Hamilton圈。将C=v1v2…vnv1作为改良圈算法的初始圈，按照以下方法，最终可得到一个最优圈C1。

1) 对于圈C所有满足1

2) 返回1)，直至无法改进，最终得到最优圈C1，停止。

1.2整数线性规划模型

为了更好地分析出行次数与时间、旅游费用等因素对线路规划的影响，首先建立仅考虑时间因素的自驾游线路规划基本模型，然后逐渐考虑其他因素的影响，并建立综合考虑年出游次数限制、单次出游时间限制以及旅游费用的线路规划模型。

1.2.1自驾游线路规划基本模型

仅考虑时间因素的情况下，要求游览全国所有5A级景点，使得游览时间最少。假设xij为旅游者从省份i到省份j旅游且每次都先抵达省会城市，tij为从省份i到省份j的自驾车时间，T0为游客游览所有景点的逗留时间，T为游客游览所有景点的总时间，可建立如下的基本模型：

目标函数：

(1)

约束条件：

(2)

(3)

(4)

(5)

1.2.2考虑出游限制的费用最优线路规划模型

在实际旅游的过程中，由于工作、家庭以及经济情况的原因，旅游爱好者不可能连续出游，每年出游的次数和每次出游的时间都会受到现实条件的约束。旅游途中，旅游费用主要由交通费用、门票费用和食宿费用3部分产生。假设M为旅游总费用，m0表示游览所有景点的门票费用，c0为日均食宿费用，ci j为旅游者从省份i到省份j旅游的油费，xi j k为旅游者第k次出游时从省份i到省份j旅游，yi k为第k次出游时游览省份i，Ti为游客游览省份i的逗留时间，λ为年出游总次数，ω为单次出游的限制时间，于是可建立费用最优线路规划模型：

目标函数：

(6)

约束条件：

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

上述模型中，满足式(6)所求的xijk即为费用最优的全国自驾游最优线路；式(7)保证每次旅游的时间不超过出游的限制时间；式(8)(9)要求各省份都被游览且只被游览一次；式(10)—(12)限制游览每个省份时，只允许从一条边进入且从一条边离开，最终回到出发地西安；式(13)是保证除出发地外，不允许走回头路；式(14)限定xi j k和yi k为0-1决策变量。

2基于改良圈算法的各省份最优线路求解结果

以四川省的5A景点作为算例，运用MATLAB软件，得到了该省的自驾线路规划图，如图1、图2所示。

图1　线路规划图(最邻近算法)Fig.1　Route programming by nearest algorithm

图2　线路规划图(改良圈算法)Fig.2　Route programming by modifeid circle algorithm

由图1，图2可知，改良圈算法求得的四川省最优线路比最邻近算法的效果明显好，且该省的最优路径为成都市区→青城山→都江堰→汶川→黄龙景区→九寨沟→北川羌城→剑门关景区→阆中古城→邓小平故里→乐山大佛→峨眉山→成都市区，距离为1 844 km。因此，可以利用改良圈算法对其他省份的自驾线路进行优化，然后可以根据各景点间的里程信息与各景点的游览时间，计算出全国各省份5A级景点的自驾游览最优时间，如表1所示。

表1　各省份5A级景点自驾游最优时间表

由表1可知，部分省份由于5A级景点较多，游览时间会比较长，如果每年出游次数和单次出游时间受到限制，每次游览的景点数也将受限，线路规划会出现大幅度的调整。

3基于整数线性规划的全国最优线路求解结果

3.1时间最优的全国自驾游线路规划结果

利用全国省会城市间的道路数据与各省份的自驾游览时间信息，运用Lingo软件，得到了时间最优的全国自驾游线路规划示意图，如图3所示。

由图3可知，全国自驾游最优路径[7]为西安→武汉→合肥→南京→上海→杭州→福州→南昌→长沙→广州→海口→南宁→昆明→贵阳→重庆→成都→拉萨→乌鲁木齐→西宁→兰州→银川→呼和浩特→太原→石家庄→北京→哈尔滨→长春→沈阳→天津→济南→郑州→西安，线路总长为19 800 km，线路总游览时间为267 d。

图3　全国自驾游线路规划图(时间最优)Fig.3　The national route programming of self-driving tour on minimum-time

3.2费用最优的全国自驾游线路规划结果

考虑到旅游爱好者每年出游的限制次数λ和每次出游的限制时间ω对其线路规划造成的影响，同时要求旅游费用尽可能节省，结合各省会城市间的道路数据和各省份的游览时间信息，利用LINGO软件，得到了当λ=2且ω=25时，费用最优的全国自驾游线路规划示意图，如图4所示。

图4　全国自驾游线路规划示意图(费用最优)Fig.4　The national route programming of self-driving tour on minimum-cost

由图4可知，由于出游时间存在约束，旅游爱好者的每次出游范围都只能局限于以西安为中心，向周边辐射的某一区域，其中成都和南京为单目的地游览线路。与时间最优的情况相比，增加了不少往返的路程，同时也增加旅游开销。为了节省一些路途时间，出行方式还可以考虑乘坐高铁或飞机到达与景区相邻的省会城市，而后采用租车的方式自驾到景区游览。但这种出行方式也会给旅游者带来一些不便，有时费用也会增加。根据线路规划的结果，得到了全国自驾游的具体行程安排以及相关费用信息，如表2所示。

表2　全国自驾游行程安排表

由表2可知，该自驾线路总游览时间为297 d，旅游总费用为110 186元。根据线路安排结果的先后顺序，大致可将全国31个省份划分为西北(新疆、西藏、青海、甘肃、宁夏、陕西)、华北(河北、天津、内蒙古、山西)、东北(黑龙江、吉林、辽宁)、华东(北京、武汉、河南、山东)、东南(福建、安徽、浙江、江苏、上海)、华南(广西、海南、湖南、广东、江西)、西南(重庆、四川、云南、贵州)等7个自驾游区域进行游览，符合实际出行的安排。

4结语

改良圈算法能够有效地解决周游型旅游爱好者的线路规划问题，能够得到比较满意的可行解，降低了线性规划法直接求解TSP问题的难度。将改良圈算法和线性规划法相结合，运用到全国5A级景区的自驾游线路优化之中，简单易懂，且线性规划法在求解景点比较少时运行速度也非常快[8]，得到的结果对实际自驾游线路的选择具有一定的指导意义。

参考文献(References)：

[1] 李勇.旅行社的自驾游业务发展策略[J].商场现代化,2007(6):109-110

LI Y.The Business Development Strategy of Travel Agency about Self-driving Tour[J].MARKET MODERNIZATION,2007(6):109-110

[2] 曹旭.旅游线路优化设计[D].兰州：西北民族大学,2012

CAO X.The Research of Tuorist Route on Optimization Design[D].Lanzhou:Northwest University for Nationalities,2012

[3] BEHDANI B,COLE S J.An Integer-programming-based Approach to the Close-Enough Traveling Salesman Problem[J].Informs Journal on Computing,2014,26(3):415-432

[4] 全惠云,江力.求解TSP的演化算法[J].湖南师范大学学报(自然科学版)：1999(2):28-34

QUAN H Y,JIANG L.An Evolutionary Algorithm for TSP[J].Hunan Normal University(Natural Science Edition),1999(2):28-34

[5] 王海莉.混合免疫算法及其应用研究[D].西安:西北大学,2005

WANG H L.Hybrid Immune Algorithm and its Application in Solving TSP[D].Xi’an:Northwest University,2005

[6] 蒋荣.遗传算法在TSP问题上的应用[D].合肥:合肥工业大学,2009

JIANG R.Genetic Algorithm and its Application in Trav-elling Salesman Problem[D].Hefei:Hefei University of Technology,2009

[7] 李旭,汪海妹,刘家保,等.基于蚁群算法的旅游线路优化研究：以合肥市为例[J].重庆工商大学学报(自然科学版)：2015(2):67-70

LI X,WANG H M,LIU J B,et al.Research on Tour Route Optimization Based on Ant Swarm Algorithm：Taking Hefei City as an Example[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2015(2):67-70

[8] 王艳红,黄华,张文娟.关于TSP问题的分块解法[J].重庆文理学院学报(自然科学版)：2008(5):32-34

WANG Y H,HUANG H,ZHANG W J.A Divided Method in Solving TSP[J].Journal of Chongqing University of Arts and Sciences(Natural Science Edition),2008(5):32-34

[9] 卢欣,李衍达.TSP问题分层求解算法的复杂度研究[J].自动化学报,1999(2):279-282

LU X,LI Y D.Complexity Analysis of the Multi-Layered Clustering Algorithm In TSP[J].Acta Automatica Sinica,1999(2):279-282

责任编辑：李翠薇

Research on the Optimization of National Self-driving Tour Route Based on Modified Circle Algorithm and Linear Programming

XIE Fei1, YANG Yang1, HE Jie2

(1.School of Information Science and Technology, Southwest Jiaotong University, Chengdu 611756, China;2.College of Civil Engineering, Southwest Jiaotong University, Chengdu 611756, China)

Abstract：Since the self-driving has many advantages, such as liberalization, customization, flexibility and comfort, now many travel enthusiasts have been attracted by self-driving. And the quality of the tourist routes may directly affect the satisfaction of self-driving tourists. In this paper, the national 5A tourist attractions are taken as the destination, a self-driving tourist in Xi’an City is selected as the research object. This article uses modified circle algorithm to design the tourist route of each province, sets the optimization of time and cost as objective function, takes the limit value of travel time per year and the limit value of single travel time as constraint condition, and builds the integer-linear programming model. The optimal self-driving tour decision of the national 5A tourist attractions is solved with LINGO software, which has a certain applicability.

Key words：TSP problem; self-driving tour; linear programming; modified circle algorithm; LINGO

中图分类号：O157

文献标志码：A

文章编号：1672-058X(2016)03-0088-06

作者简介：谢飞(1990-),男,四川内江人,硕士研究生,从事铁路信号控制研究.

收稿日期：2015-11-09；修回日期：2015-12-25.

doi:10.16055/j.issn.1672-058X.2016.0003.018