拟定生产计划的多变量条件下的线性规划模型

李小卉

摘 要：拟定生产计划是生产生活中常出现的一个问题，本文就合金的制造给出的生产和订购决策问题进行研究，展开讨论，分析和建立数学模型，利用数学软件lingo进行求解。只考虑包含一家公司和一份订单的供应链，这家公司的原材料的信息是已知的，订单量也是确定的，在此条件下找好目标函数与约束条件，建立线性规划模型进行求解，当这家公司满足订单要求时所需的成本最低就是此题的最优解，最后利用lingo软件进行编程求解确定这家公司的原材料的取法。

关键词：生产计划；lingo软件；线性规划

一、问题背景与重述

（一）问题的背景

中国自古就是个钢铁大国，钢铁用于各行各业，由于对钢铁的性能高要求，合金制造商家必须用合理的原材料组配炼出高性能的钢铁合金以迎合市场要求，同时使自身获利更多，而造船用钢是指用于制造海船和大型内河船体结构的钢，它除了要有良好的焊接性能，还要求有一定的强度、韧性和一定的耐低温及腐蚀性能，这种钢一般使用合金制造而成。

（二）问题的重述

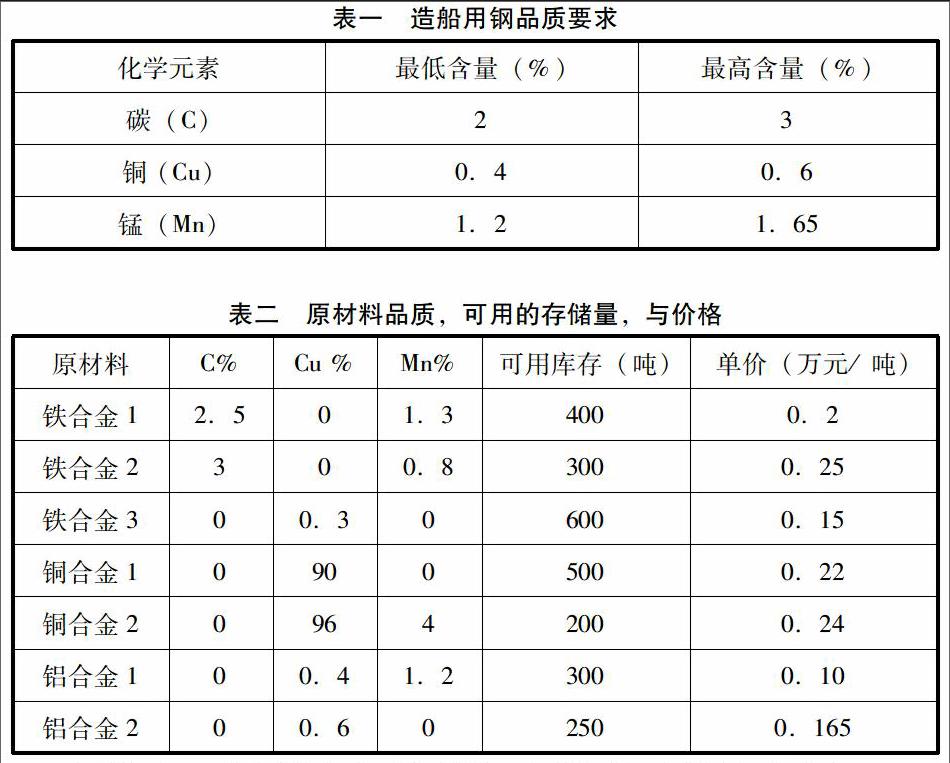
一家钢铁公司收到一份500吨造船用钢的订单，对这些造船用钢有如下要求（品质）：

此公司储存有7种不同的原材料，都可以用于制造这种钢。

问题（1）：为了使生产成本最低，各种原材料应该各取多少。

问题（2）：如果铁合金1的可用库存为380吨，其他条件不变，问此时怎样选取各种原材料。

问题（3）如果铝合金1的价格上50%，其他条件不变，此时又该怎样选取各种原材料。

二、模型假设

假设订单的要求不会在生产途中有所改变；每种原材料的取用量可随意假设钢铁造船时无耗损，即生产的合金全造成船；不考虑其他费用成本仅是钢铁材料的花费；原材料的品质是确定的，即在单位质量的原材料中所含杂质的量是一定的，不会因为取料的多少而改变任意杂质的含量。

三、符号说明

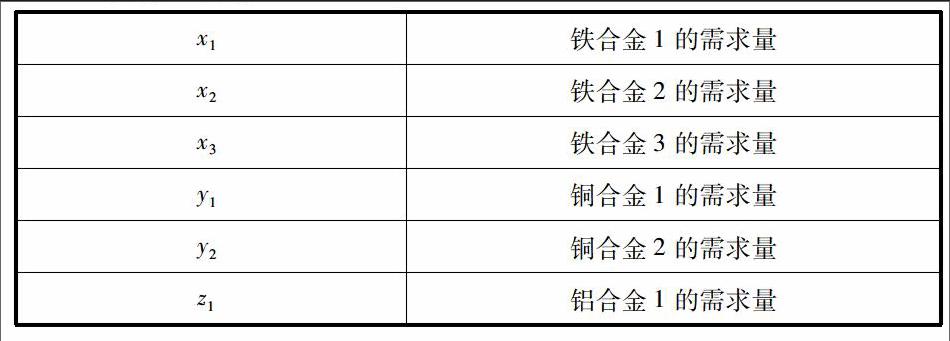
x1铁合金1的需求量

x2铁合金2的需求量

x3铁合金3的需求量

y1铜合金1的需求量

y2铜合金2的需求量

z1铝合金1的需求量

z2铝合金2的需求量

P生产成本

四、问题分析

这是一个线性规划问题，要决定的是这家钢铁公司的最优的生产方案，完成此方案需满足两个条件，其一为使生成本最低的目标函数，但在现实生活中所需条件通常并非那么理想，这就构成了所需的第二个条件——约束条件。

对本题这家钢铁公司原材料的信息与订购量都是明确的，目标函数的确定是显然的，而约束条件分为三小点：1.对杂质含量约束；2.对可用库存的约束；3.对订单所需总量的约束，分别用数学表达式表达上述条件，然后用lingo软件即可求解。

五、模型建立

对于问题（1）的求解：

六、模型求解及结果分析

（一）模型求解结果

根据我们建立的模型结果如下表：

（二）结果分析

1、问题（1）为了使生产成本最低，各种原材料应该各取多少？

由此解得用铁合金1量为400吨、铜合金1量为1.7吨、铝合金1量为98.2吨锻造此合金时可使总花费最低为90.2万元。

另外我们还可以得出：当碳最低含量减少1个单位时，总花费减少20.1，当碳最高含量减少或增加1个单位时，总花费不变，当铜最低含量减少1个单位时，总花费减少0.6，当碳最高含量减少或增加1个单位时，总花费不变，当合金总重即生产能力减少1个单位时，总花费减少0.1。

2、问题（2）如果铁合金1的可用库存为380吨，其他条件不变，问此时怎样选取各种原材料？

用铁合金1量为380吨、铁合金2量为16.7吨、铜合金1量为1.7吨、铝合金1量为101.5吨锻造此合金时可使总花费最低为90.7万元。

另外我们还可以得出：当碳最低含量减少1个单位时，总花费减少25.1，当碳最高含量减少或增加1个单位时，总花费不变，当铜最低含量减少1个单位时，总花费减少0.7，当铜最高含量减少或增加1个单位时，总花费不变，当合金总重即生产能力减少1个单位时，总花费减少0.2，当铁合金1的库存量增加1个单位时，总花费降低0.2491071E-01。

3、问题（3）如果铝合金1的价格上50%，其他条件不变，此时又该怎样选取各种原材料？

用铁合金1量为400吨、铜合金1量为1.79吨、铝合金1量为98.21吨锻造此合金时可使总花费最低为95.125万元。

另外我们还可以得出：当碳最低含量减少1个单位时，总花费减少10.11，当碳最高含量减少或增加1个单位时，总花费不变，当铜最低含量减少1个单位时，总花费减少0.3，当铜最高含量减少或增加1个单位时，总花费不变，当合金总重即生产能力减少1个单位时，总花费减少0.1902500。

七、模型评价与推广

模型的优点：该模型较客观的反映了在确定条件下的线性规划问题，模型简单明了，易于编程求解；模型的缺点：该模型题目条件过于理想，所考虑的不变因素过少，不太可能在实际生产生活中进行推广。

模型推广：可用库存与单价也是可以变动的；本模型可以推广到多家钢铁公司与多份订单的模型，多份订单的要求可以不同；合金中杂质的含量可以与所用该合金的多少有关，即单位质量的某种杂质的含量的多少是有一波动区间，但所取该合金量越多此波动区间越小。

参考文献：

[1] 宋来忠、王志明，数学建模案与实验，科学出版社，2005年。

[2] 袁新生、绍大宏、郁时炼，LINGO和Excel在数学建模中的应用，高等教育出版社，2006年。