乘积季节模型ARIMA(p,d,q)×(P,D,Q)s在CPI分析中的应用

黄 艳 华

(重庆工商大学 数学与统计学院，重庆 400067)



乘积季节模型ARIMA(p,d,q)×(P,D,Q)s在CPI分析中的应用

黄 艳 华

(重庆工商大学 数学与统计学院，重庆 400067)

摘要：居民消费价格指数CPI，是衡量通货膨胀的重要参考指标之一，是国家制定宏观经济政策的依据。选用2000年1月至2015年8月的最新月度CPI数据，采用静态预测与动态预测相结合的分析方法构建了乘积季节模型；分析结果表明，模型的预测精度较高，预测误差为0.281 54，因此，CPI的预测结果可为宏观经济调控政策的制定提供参考。

关键词：CPI;乘积季节模型;静态预测;动态预测

居民消费价格指数CPI，是衡量通货膨胀的重要参考指标之一，是国家制定宏观经济政策的依据，其变动率在一定程度上反映了通货膨胀或紧缩的程度。按照价格上升的速度，西方学者认为存在3种类型的通货膨胀：第一，温和通货膨胀，每年物价上升的比例在10%以内，一些人认为温和通货膨胀对经济和收入的增长有积极的刺激作用。第二，奔腾的通货膨胀，每年物价上升的比例在10%～100%，一些人认为奔腾的通货膨胀发生后，公众会采取各种措施保护自己，以免受通货膨胀之害，通货膨胀会更为加剧。第三，超级通货膨胀，每年物价上升的比例在100%以上，发生超级通货膨胀的结果是，人们对货币完全失去信任，各种正常的经济联系遭到破坏，以致货币体系和价格体系最后完全崩溃，在严重的情况下，会出现社会动乱。因此唯有准确把握CPI走势，方可采取有效的措施将奔腾通货膨胀和超级通货膨胀扼杀在摇篮之中。

通过对CPI相关文献的研读，选用2000年1月至2015年8月的最新月度CPI数据，构建了季节乘积模型ARIMA(p,d,q)×(P,D,Q)s，在静态预测方法拟合精度较高的基础上，采用动态预测方法分析CPI走势。结果表明，文章所建立的模型预测精度较高，预测结果可靠。

1季节乘积模型与数据选取

乘积季节模型ARIMA(p,d,q)×(P,D,Q)s可以描述任何齐次非平稳时间序列，它是最一般的表示形式，包括AR(p)，MA(q)，ARMA(p,q)，ARIMA(p,d,q)，ARIMA(P,D,Q)s以及各种组合模型。

1.1乘积季节模型

建立乘积季节模型的步骤为平稳性检验，模型的识别，模型的参数估计，模型的分析与评价，利用拟合模型预测序列的未来走势。对时间序列平稳性的检验主要有两种方法，自相关图和单位根检验。单位根检验目前最常用的方法为ADF检验和PP检验。模型识别的基本工具是相关分析，根据样本序列的自相关与偏自相关函数所表现出来的某些特性，如拖尾性、截尾性、周期性，进而选定合适的模型拟合样本数据。此过程可归纳为3步：首先差分化，确定d,D；其次为非季节数据选择p,q；最后为季节数据选择P,Q。利用有关的时间序列样本数据，提出值得考虑的模型，确定模型的类型及相应的阶数p,d,q,P,D,Q。模型权衡取舍的依据是最小信息准则，如AIC，SC，HQ准则。

乘积季节模型的结构如下：

其中，Φ(B)=1-φ1B-…-φpBp；ΦS(B)=1-φ1BS-…-φpBPS；Θ(B)=1-θ1B-…-θqBq；ΘS(B)=1-θ1BS-…-θqBQS。

模型的适应性检验实际上就是检验模型的残差序列{at}是否为白噪声序列，如果模型的残差序列为白噪声序列，则模型通过白噪声检验，模型对时间序列信息的提取充分，否则需要对模型进行优化，拟合适应的模型。

模型的分析与评价包括两方面内容：对历史数据的拟合和对未来趋势的反应。只有当模型对历史数据拟合较好，并且符合时间序列未来的发展趋势时，模型才能用于预测。

1.2数据分析处理

将中国2000年1月至2015年8月的最新月度CPI(上年同期为100)数据转换为定基数据，并将基期固定为2000年。数据来源于中华人民共和国国家统计局官方网站http://www.stats.gov.cn/。用2000年1月至2014年12月的数据建立模型，用预留数据检验模型的预测精度。所有的分析均通过Eviews 8.0 完成。

根据季节乘积模型建模要求，采用ADF单位根检验判断CPI序列的平稳性。由表1可知，t统计量的实际值0.041 743大于各显著性水平下的临界值，即CPI序列未通过单位根检验，因此CPI序列为非平稳序列。将CPI序列进行一阶差分记为DCPI，采用ADF单位根检验判断DCPI序列的平稳性。由表2可知，t统计量的实际值 -2.955 376小于5%显著性水平下的临界值，即DCPI序列通过单位根检验，因此DCPI序列为平稳序列。

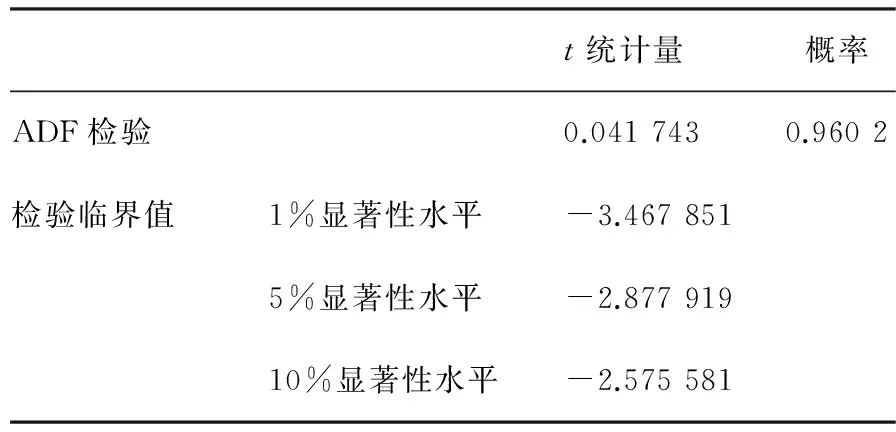
表1　CPI单位根检验

原假设：CPI序列存在单位根；外源性为常数；延迟阶数为12。

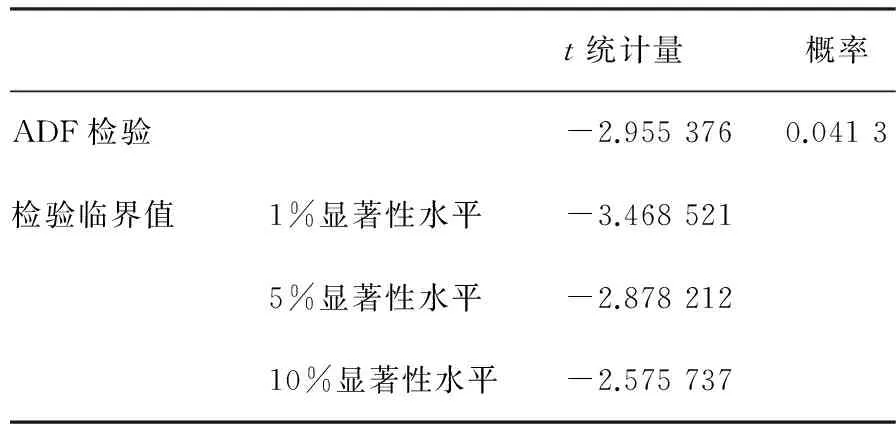
表2　DCPI单位根检验

原假设：DCPI序列存在单位根；外源性为常数；延迟阶数为14。

2实证分析

2.1模型的识别与建立

图1为DCPI序列的自相关关系图。由图1可知，延迟12阶的自相关与偏自相关系数显著大于2倍的标准差范围之外，显著不为0，因此DCPI序列存在季节性，即周期性的变化规律，每隔12个月重复这一规律。为消除DCPI序列的季节性，对其进行周期长度为s=12的一阶季节差分。季节差分之后，序列记为SDCPI。 图2为SDCPI序列的自相关关系图。由图2可知，经季节差分之后，季节性有所削弱，但并未基本消除。考虑对其进行二阶季节差分，但发现序列的季节性依然无法消除，因此只进行一阶季节差分。

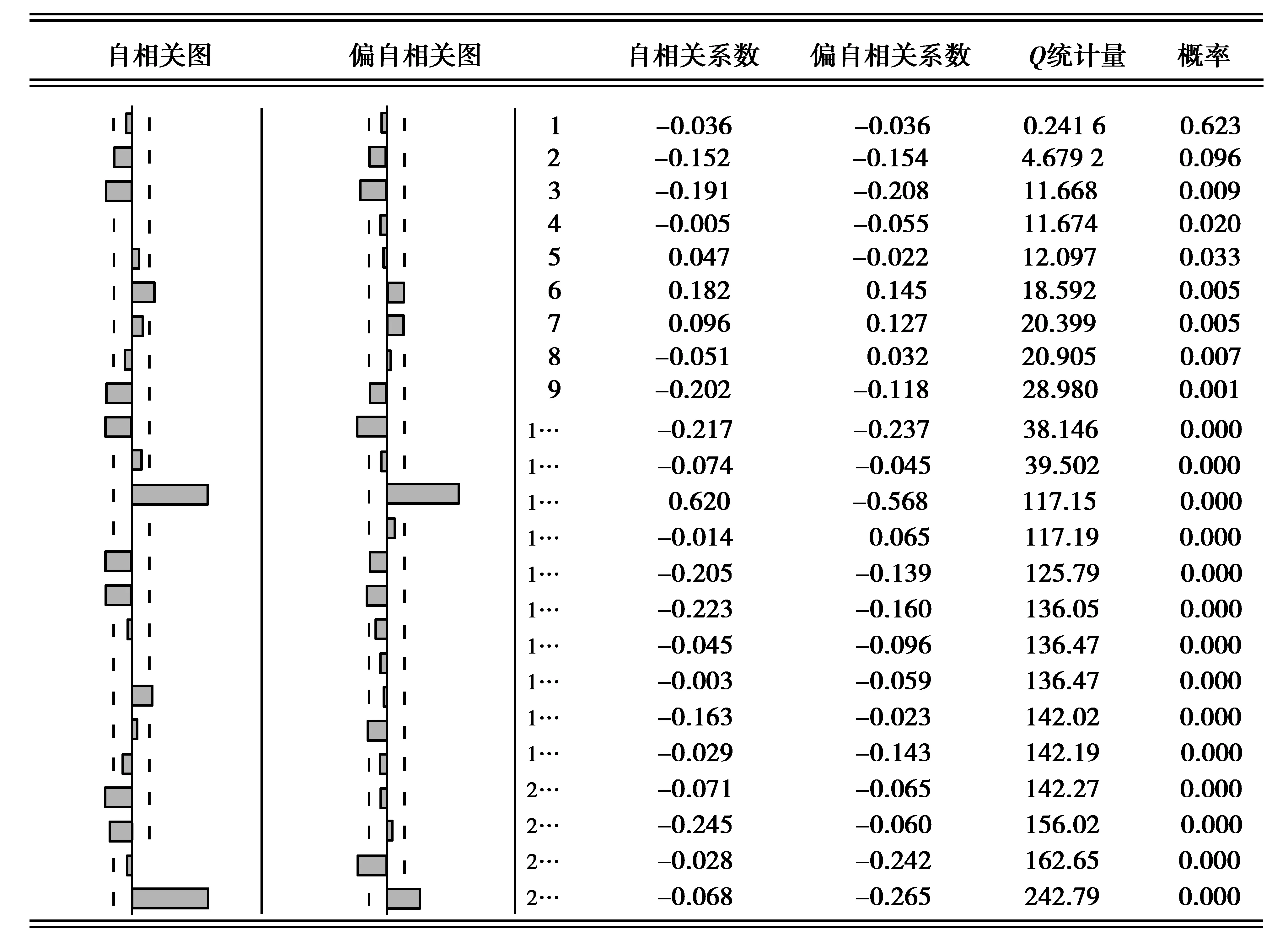
图1　DCPI自相关关系图Fig.1　DCPI auto correlation diagram

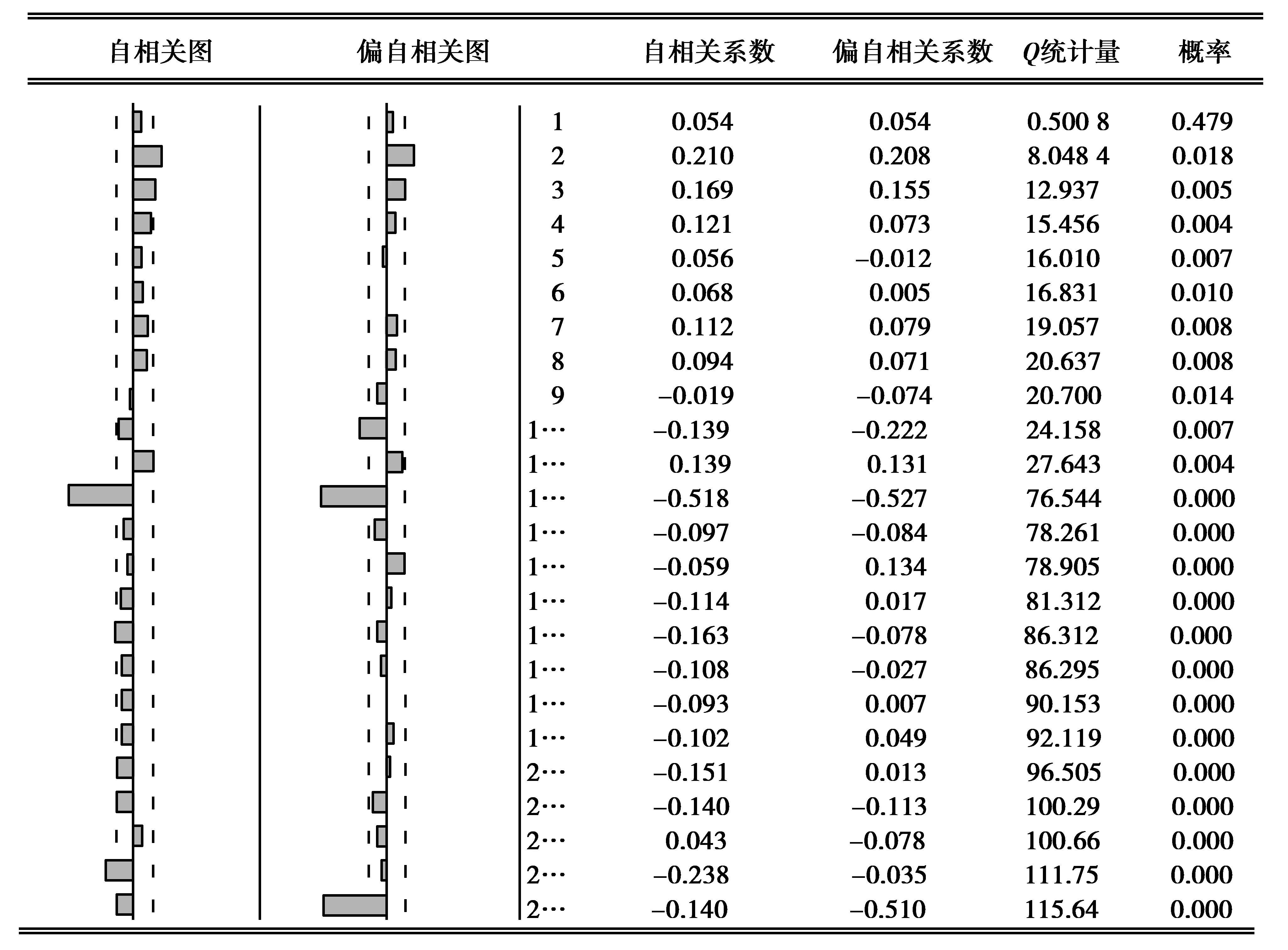
图2　SDCPI自相关关系图Fig.2　DCPI auto correlation diagram

由图2可知，时滞12以内，显著不为0的偏自相关个数为3(k=2,k=12，k=10)，可以考虑初选p=3；显著不为0的自相关个数为2(k=2,k=12)，可以考虑初选q=2；当k=12和k=24时，偏自相关系数显著的不为0，因此选择P=2；当k=12时，自相关系数显著的不为0，因此选择Q=1。

因此初选模型为ARIMA(3,1,2)×(2,1,1)12，ARIMA(3,1,1)×(2,1,1)12，ARIMA(4,1,1)×(2,1,1)12。模型初步选定之后，就要对模型进行参数显著性检验，并根据AIC准则选择最优模型。各模型的估计结果分别为表3、表4和表5。对比分析后， ARIMA(3,1,2)×(2,1,1)12暂定为最优模型。

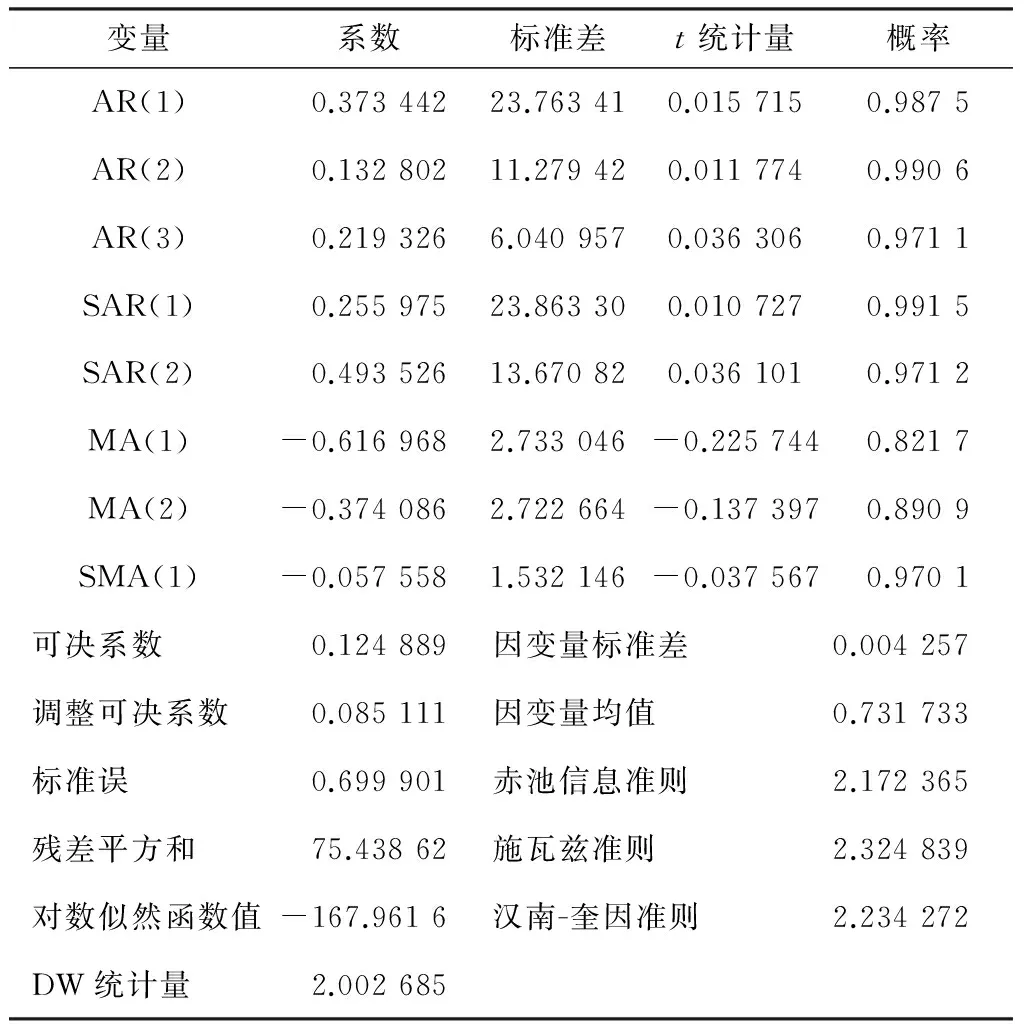
表3　ARIMA(3,1,2)×(2,1,1)12

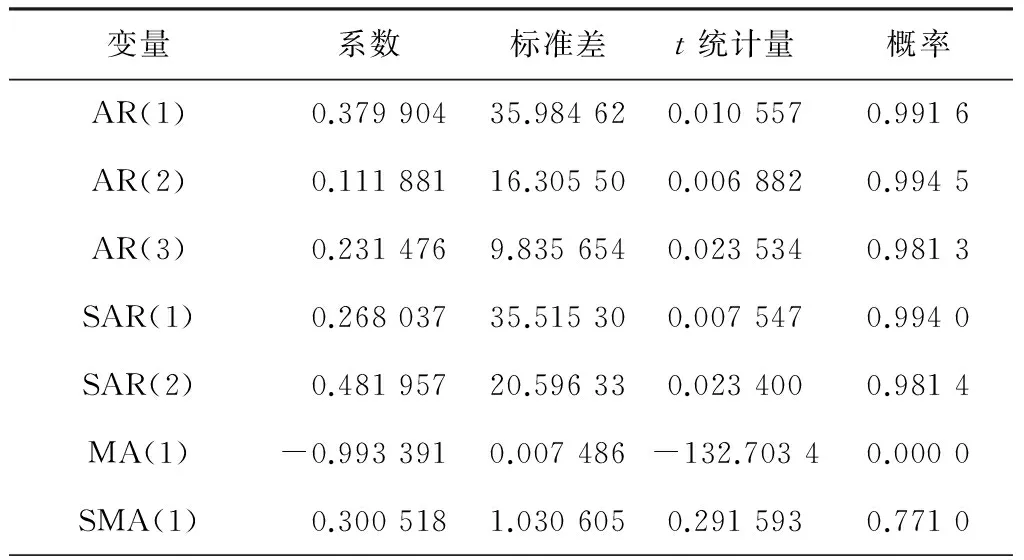
表4　ARIMA(3,1,1)×(2,1,1)12

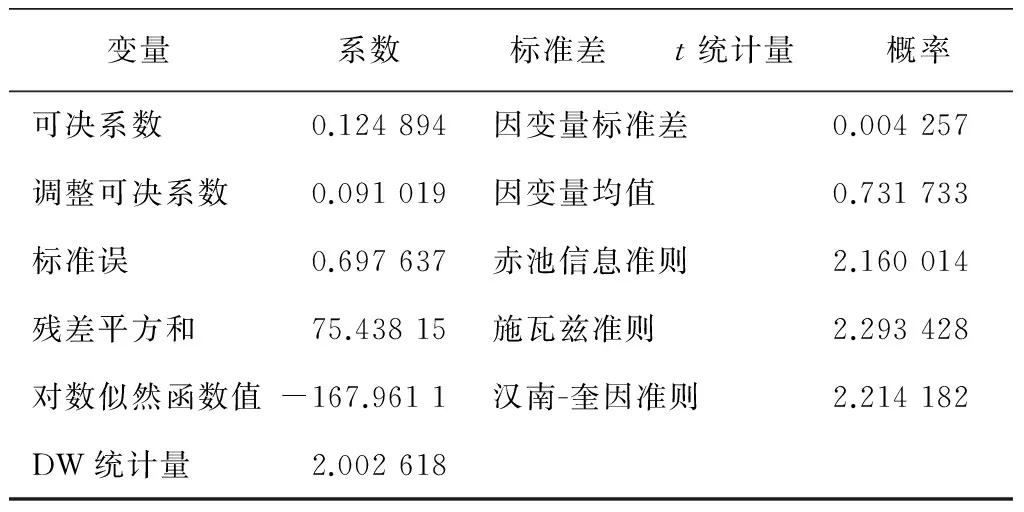
续表(表4)

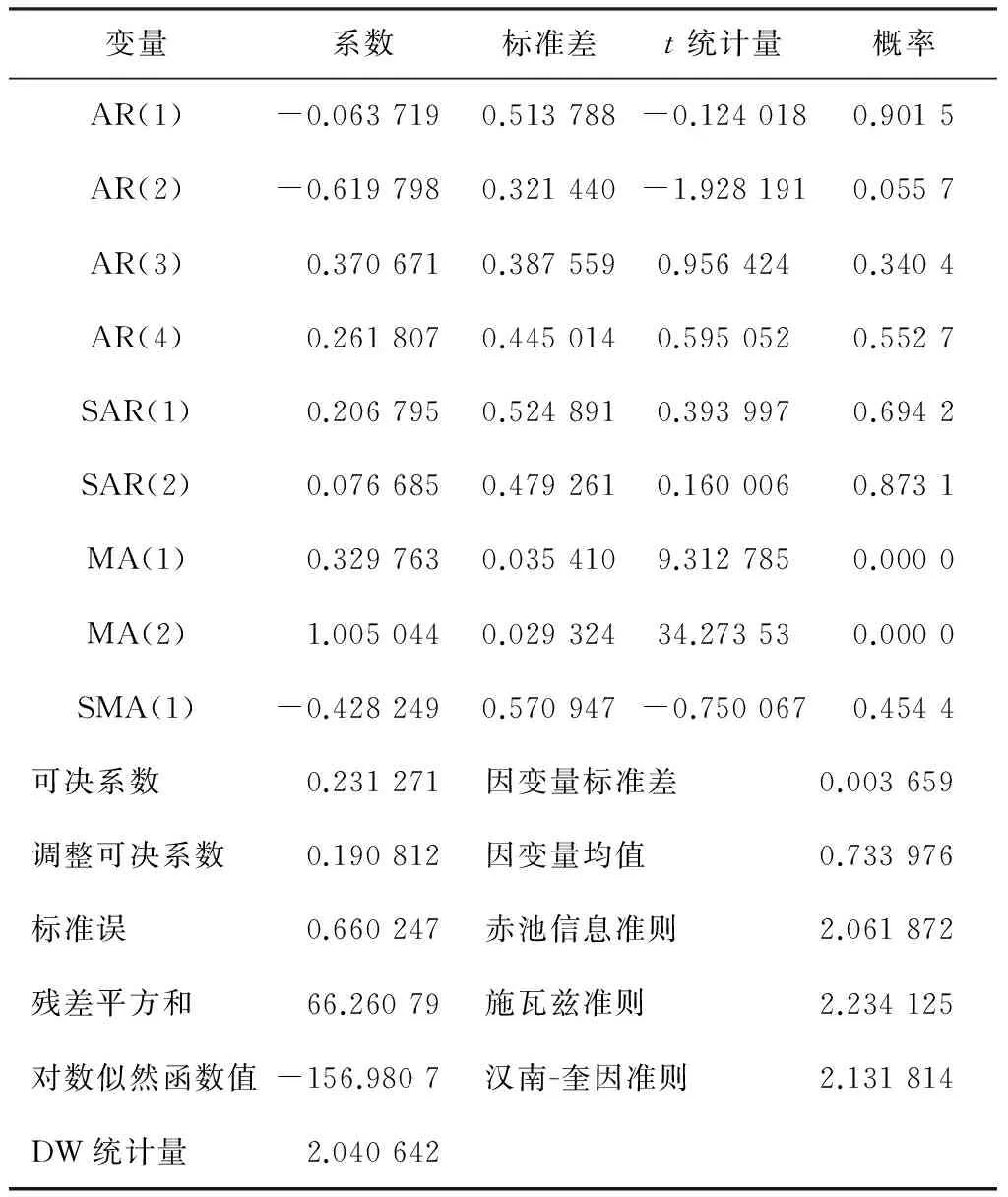
表5　ARIMA(4,1,1)×(2,1,1)12

2.2模型的检验

检验模型ARIMA(3,1,2)×(2,1,1)12的残差序列是否为白噪声序列，从而判定该拟合模型是否有效。若残差序列是白噪声序列，则说明模型已经全面提取了数据所包含的信息，模型通过适应性检验，此处采用Q统计量检验模型残差序列的相关性，结果为图3。各滞后阶数的自相关与偏自相关都接近于零，并且Q统计量的P值较大，因此残差序列为白噪声序列。因此ARIMA(3,1,2)×(2,1,1)12为最优模型。

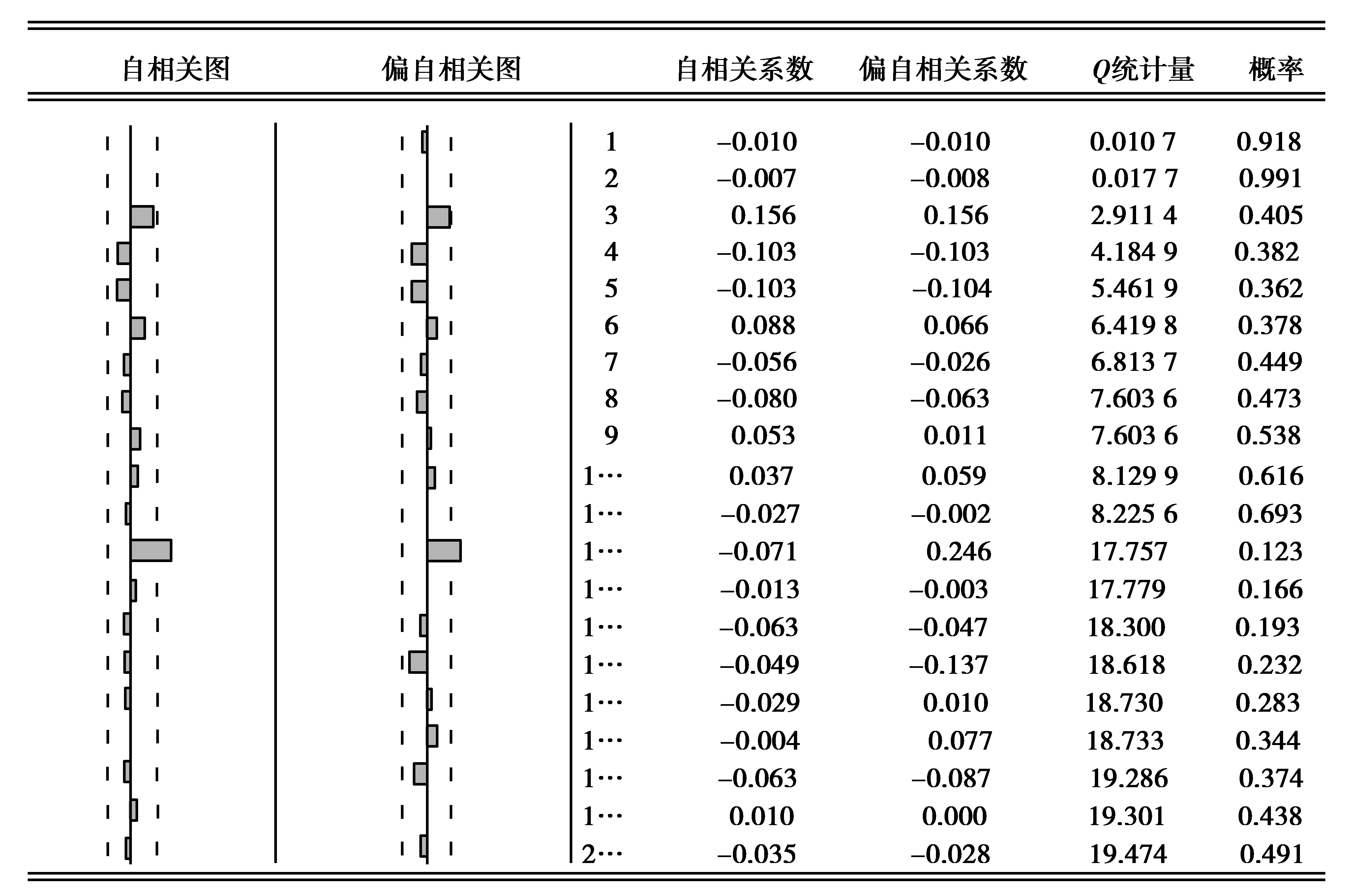
图3　模型残差相关关系图Fig.3　Model residuals correlation diagram

2.3模型的分析与预测

使用模型 ARIMA(3,1,2)×(2,1,1)12，采用静态分析方法拟合历史数据，对样本期内模型的拟合效果进行分析。2000年1月至2014年12月拟合误差为MAPE=0.443 144，2010年1月至2014年12月拟合误差为MAPE=0.367 711。整个样本期和近期误差MAPE<10，模型的预测精度较高；近期误差比整个样本期小，说明模型对近期的预测变好。图4为整个样本期内CPI的真实值与模型估计值CPIF的序列图。由图4可以看出拟合序列与原序列的变化趋势基本一致。

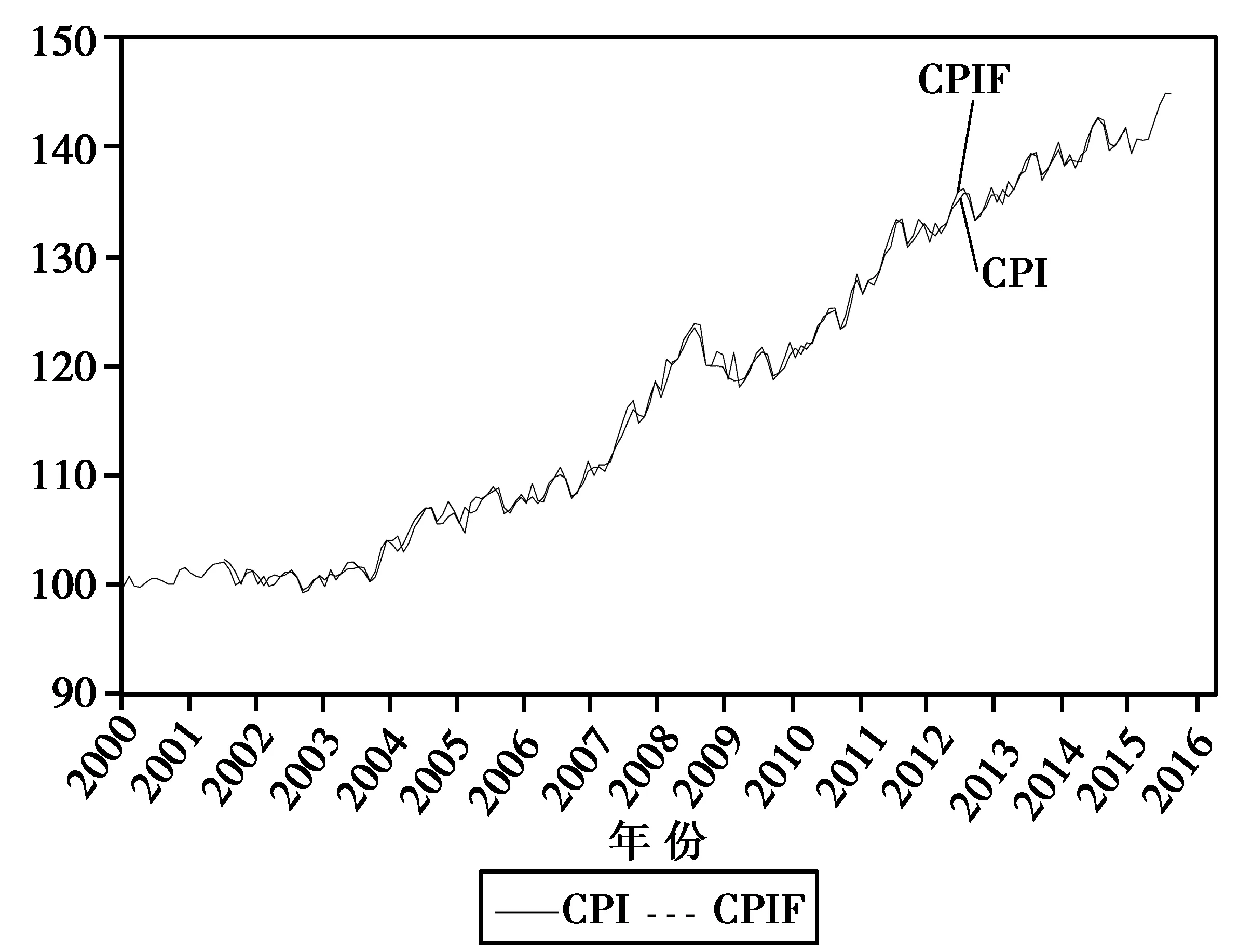
图4　CPI真实值与预测值Fig.4　CPI real and predicted values

因此ARIMA(3,1,2)×(2,1,1)12模型可用于预测2015年年末及2016年年初CPI走势，用预留数据做误差分析。分析结果表明：预测误差为MAPE=0.281 54，因此2015年年末及2016年年初的CPI预测结果可靠，且具有较高的精度。2015年年末及2016年年初CPI真实值与预测值为表6。

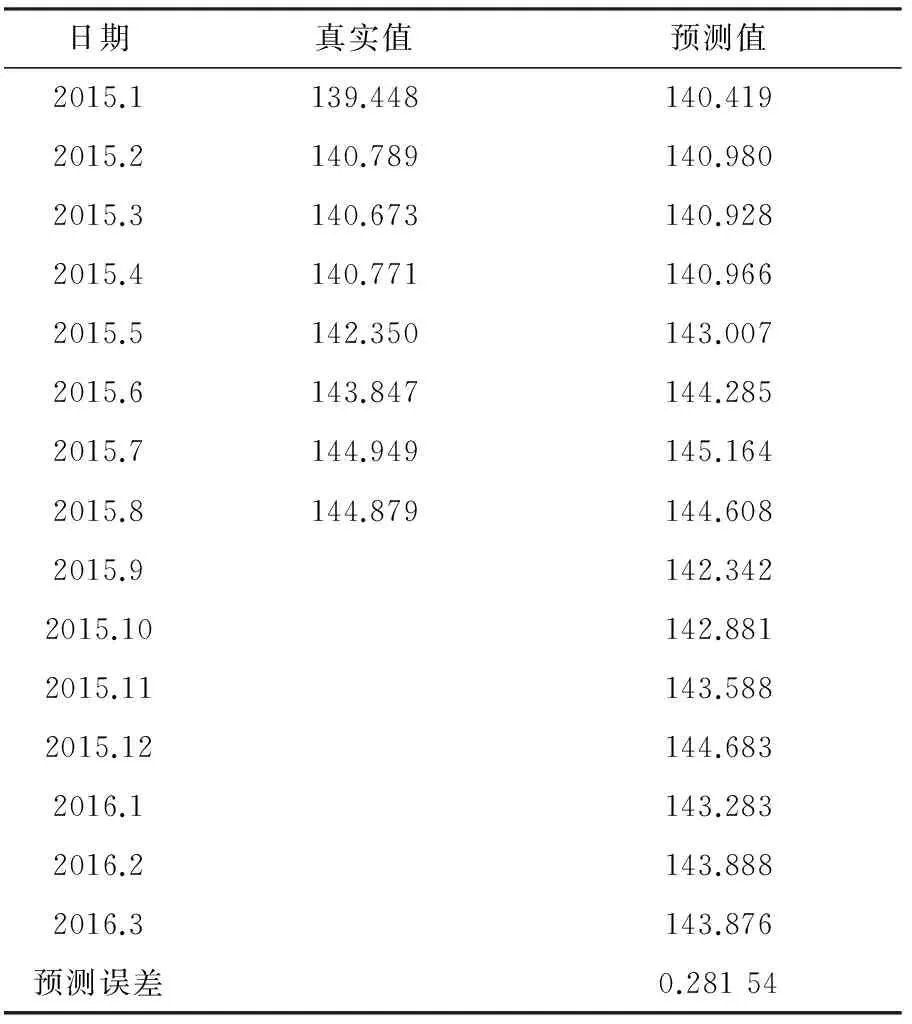
表6　CPI真实值与预测值

3结论

将定基处理的CPI时间序列数据分为两部分，2000年1月至2014年12月用于建模，2015年1月至2015年8月用于试点预测的测试集。通过成熟的时间序列建模技术，建立了具有较高预测精度的乘积季节模型ARIMA(3,1,2)×(2,1,1)12，预测误差为MAPE=0.281 54。由预测结果可以看出，2015年9月至2016年3月，CPI呈现下降-上升-下降的循环波动，但波动幅度小。元旦与春节期间人们会购买大量商品，在此期间可能会出现供不应求现象，此现象将导致通货膨胀问题的出现。分析结果表明，在元旦与春节期间CPI上升，确实存在一定程度的通货膨胀，由于通货膨胀的幅度较小，属于温和通货膨胀，因此政府无需强加干涉。分析结果符合社会经济规律，因此构建的乘积季节模型ARIMA(3,1,2)×(2,1,1)12不仅具有较高预测精度，而且预测结果可靠。

参考文献(References)：

[1] 张建.SARIMA模型在预测中国CPI中的应用[J].统计与决策,2011(5):28-30

ZHANG J.The Application of SARIMA Model in Predicting China CPI[J].Statistics and Decision,2011(5):28-30

[2] 郭晓峰.基于ARIMA模型的中国CPI走势分析[J].统计与决策,2012(11):29-32

GUO X F.China’s CPI Trend Analysis Based on the ARIMA Model.[J].Statistics and Decision,2012(11):29-32

[3] 雷鹏飞.基于季节性ARIMA模型的中国CPI序列分析与预测[J].统计与决策,2014(14):32-34

LEI P F.China’s CPI Series Analysis and Prediction Based on Seasonal ARIMA Model[J].Statistics and Decision,2014(14):32-34

[4] 易丹辉.时间序列分析方法与应用[M].北京：中国人民大学出版社,2011

YI D H.Time Series Analysis and Application[M].Beijing:China Renmin University Press,2011

[5] 王燕.应用时间序列分析[M].北京：中国人民大学出版社,2008

WANG Y.Time Series Analysis[M].Beijing:China Ren min University Press,2008

[6] 王振龙,胡永宏.应用时间序列分析[M].北京：科学出版社,2007

WANG ZH L,HU Y H.Time Series Analysis[M].Beijing:Science Press,2007

责任编辑：李翠薇

Application of Multiplicative Seasonal Model ARIMA(p,d,q)×(P,D,Q) to CPI Analysis

HUANG Yan-hua

(School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)

Abstract：Consumer Price Index (CPI) is one of important references to measure inflation and is the basis for a nation to make macroeconomic policy. This paper chooses latest monthly CPI data during January, 2000-August, 2015 to construct Multiplicative Seasonal Model and uses the combination of static prediction and dynamic prediction to conduct the analysis. The analysis result shows that the prediction precision of the Model is relatively high, prediction deviation is MAPE=0.281 54, therefore, CPI prediction result can provide Combined Forecast of China reference for making macroeconomic regulation policies.

Key words：CPI; Multiplicative Seasonal Model; static prediction; dynamic prediction

中图分类号：O212

文献标志码：A

文章编号：1672-058X(2016)03-0070-06

作者简介：黄艳华(1990-)，女，河南周口人，硕士，从事统计理论与方法研究.

收稿日期：2015-10-16；修回日期：2015-12-02.

doi:10.16055/j.issn.1672-058X.2016.0003.015