Hs(RR3)空间内非线性混合Schrödinger方程组解的唯一性

贾翠

（湖北汽车工业学院理学院，湖北十堰442002）



Hs(RR3)空间内非线性混合Schrödinger方程组解的唯一性

贾翠

（湖北汽车工业学院理学院，湖北十堰442002）

摘要：依据仿积技术和Besov空间，以Schrödinger容许对为切入点，证明了当时，三维空间中的非线性混合Schrödinger方程组系统中的解的无条件唯一性。

关键词：唯一性；Strichartz估计；仿积估计；Hölder不等式

oi：10.3969/j.issn.1008-5483.2016.01.016

0　引言和主要结果

考虑如下非线性混合Schrödinger方程组

混合Schrödinger方程组（1）是由Manakov和Zakharov在考虑完整积分和离散动力学的Stochas⁃tization时引入的。

简单地回顾一些PDE问题的解的无条件唯一性的结果。在和基于先验估计的辅助空间（Strichartz空间，平滑空间，…）框架内常运用不动点理论构造强解。在辅助空间内解的唯一性称为有条件的唯一性。另一方面，无辅助空间的唯一性称为无条件唯一性。涉及到的无条件唯一性的参考文献主要是关于Schrödinger方程［1-9］，波动方程［4，10-13］，Navier-Stokes系统［14］，Benjamin-Ono方程［15］，Zakharov系统和Maxwell-Dirac方程情形［16-17］，Klein-Gorden-Schödinger系统［18］和Dirac-Klein-Gorden方程［19］。

基于以上结果，本文的目的是证明系统（1）的解的无条件唯一性。关于非线性混合Schrödinger方程组（1），研究过H1(R3)空间中解的局部适定性。因此，可以总结非线性混合Schrödinger方程组（1）的局部适定性如下：

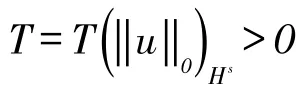
有解的局部适定性，一个很自然的问题是这个解是不是无条件唯一的。现陈述主要结果。

1　符号和预备知识

1.1符号

是有界的，当r=∞作一些必要的修改。引进时空Lebesgu空间的范数为

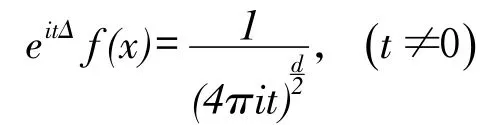
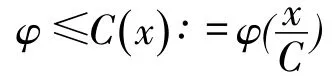
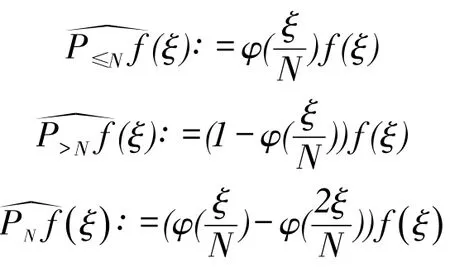
再回顾齐次空间Ḃsp,q的定义。对任一

1.2一些估计

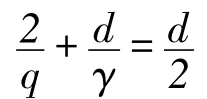
运用Hölder’s不等式和Sobolev嵌入，得到引理2~4。

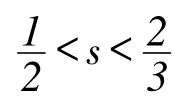
下述仿积引理是证明主要结果的关键工具，可用仿积估计证明。

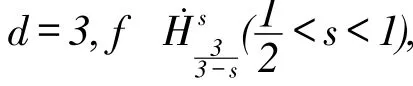
2　主要结果的证明

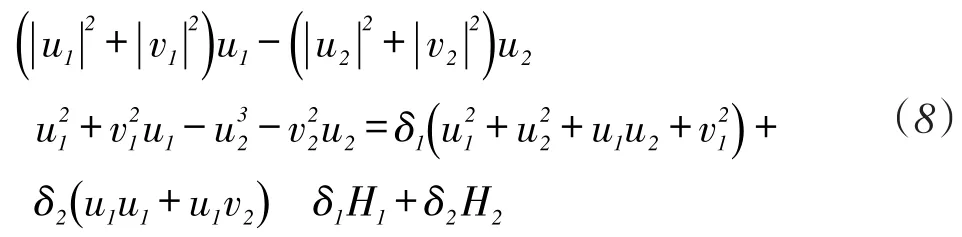
参考文献：

［1］T Cazenave，F Weissler. The Cauchy Problem for the Critical Nonlinear Schrödinger Equations in HS［J］. Non⁃linear Analysis：Theory, Methods & Applications, 1990, 14（10）：807-836.

［2］T Kato. On nonlinear Schrödinger Equations，II. HS-solu⁃tions and Uncontitional Well-Posedness［J］. Journal d’Analyse Mathématique，1995，67（1）：281-306.

［3］T Keel，T Tao. Endpoint Strichartz Estimates［J］. Amer J Math, 1998，120（5）：955-980.

［4］Furioli G，Planchon F，Terraneo E. Unconditional Wellposedness for Semilinear Schrödinger and Wave Equa⁃tions in HS［J］. Contemporary Mathematics，2003，320：147-156.

［5］Rogers K M. Unconditional Well-posedness for Subcriti⁃cal NLS in HS［J］. Comptes Rendus Mathematique, 2007，345（7）：395-398.

［6］Yin Yin Su Win，Tsutsumi Y. Unconditional Uniqueness of Solution for the Cauchy Problem of the Nonlinear Schrödinger Equation［J］. Hokkaido Mathematical Jour⁃nal，2008，37（4）：839-859.

［7］Furioli G，Terraneo E. Besov Spaces and Unconditional Well-posedness for the Nonlinear Schrödinger equation in HS(Rn)［J］. Commun Contemp Math, 2003，5（3）：349-367.

［8］Triebel H. Theory of Function Spaces［M］. Basel：Birkhäuser，1983.

［9］T Cazenave. Courant Lecture Notes in Mathematics：Vol⁃ume 10 Semilinear Schrödinger Equations［M］. Wash⁃ington D.C.：American Mathematical Society, 2003.

［10］Bulut A，Czubak M，Dong L，et al. Stability and Uncon⁃ ditional Uniqueness of Solutions for Energy Critical Wave Equations in High Dimensions［J］. Communica⁃tions in Partial Differential Equations，2013，38（4）：575-607.

［11］Masmoudi N，Planchon F. On Uniqueness for the Criti⁃cal Wave Equation［J］. Communications in Partial Dif⁃ferential Equations，2006，31（7）：1099-1107.

［12］Planchon F. On Uniqueness for Semilinear Wave Equa⁃tions［J］. Math Z, 2003，244（3）：587-599.

［13］Struwe M. Uniqueness for Critical Nonlinear Wave Equa⁃tions and Wave Maps via the Energy Inequality［J］. Comm Pure Appl Math，1999，52（9）：1179-1188.

［14］Fujita H，Kato T. On the Navier-Stokes Initial Value Problem I［J］. Arch Rational Mech Anal，1964，16 （4）：269-315.

［15］Burq N，Planchon F. The Benjamin-Ono Equation in Energy Space，Phase Space Analysis of Partial Differen⁃tial Equations［J］. Progr Nonlineqr Differential Equa⁃tions，2006，69：55-62.

［16］Masmoudi N，Nakanishi K. Uniqueness of Solutions for Zakharov Systems［J］. Funkcial Ekvac，2009，52（2）：233-253.

［17］Masmoudi N，Nakanishi K. Uniqueness of finite energy solutions for Maxwell-Dirac and Maxwell-Klein-Gor⁃den Equations［J］. Comm Math Phys，2003，243（1）：123-136.

［18］H Pecher. Some New Well-posedness Results for the Klein- Gorden- Schrödinger System［J］. Differential And Integral Equations, 2011，25（1/2）：117-142.

［19］Selberg S，Tesfahun A. Remarks on Regularity and Uniqueness of the Dirac- Klein- Gorden Equations in one Space Dimension［J］. NoDEA Nonlinear Dfferrn⁃tial Equations and Applications，2010，17（4）：453-465.

Unconditional Uniqueness for Nonlinear Coupled Schrödinger Equations in Hs（)

Jia Cui
（School of Science, Hubei University of Automotive Technology, Shiyan 442002, China）

Abstract:According to the paraproduct techniques and Besov spaces, based on Schrödinger-admissible pairs, the unconditional uniqueness of the solutions to the system of the nonlinear coupled Schrödinger equation in Ct(Hs)was provedKey words: uniqueness; Strichartz estimation; praproduct estimation; Hölder inequality

作者简介：贾翠（1988-），女，山东泰安人，硕士，从事应用数学方面的研究。E-mail：jiacui3621651@163.com

收稿日期：2015-10-31

中图分类号：O175.29

文献标识码：A

文章编号：1008-5483（2016）01-0067-04 d